[Paper 리뷰] Efficient Speech Language Modeling via Energy Distance in Continuous Latent Space

Efficient Speech Language Modeling via Energy Distance in Continuous Latent Space

---

• Speech language model은 discretization으로 인한 한계가 있음
• SLED
  • Speech waveform을 continuous latent representation의 sequence로 encoding
  • Energy distance objective를 사용하여 autoregressive modeling을 수행
• 논문 (NeurIPS 2025) : Paper Link

---

1. Introduction

• Speech audio는 integer/floating-point range내의 value를 가지는 lengthy sampling point sequence로 represent 됨
  • 이때 autoregressive modeling을 수행하기 위해서는 HuBERT, EnCodec, DAC, SpeechTokenizer와 같은 external quantization module을 사용하여 speech를 discrete token sequence로 discretizing 해야 함
  • BUT, discretization은 inevitable information bottleneck으로 인해 waveform의 rich detail을 loss 할 수 있음
    1. 이를 해결하기 위해 SoundStream과 같이 Residual Vector Quantization (RVQ)를 활용하여 raw waveform을 multi-stream sequence로 convert 할 수 있음
    2. BUT, RVQ는 additional complexity가 존재하므로 multi-stream sequence를 effectively modeling 하기 위해서는 hierarchical autoregressive architecture가 필요함
  • 이와 달리 continuous latent space에 대한 speech modeling은 다음의 장점을 제공함:
    1. Discretization이 사용되지 않으므로 information loss 없이 latent space에서 modeling을 수행할 수 있음
    2. RVQ와 같은 hierarchical architecture에 대한 의존성을 피해 modeling complexity를 줄일 수 있음

-> 그래서 continuous latent space를 활용한 speech language model인 SLED를 제안

 

• SLED
  • Lightweight implicit conditional generative module을 통해 per-step continuous distribution을 modeling
  • Underlying data distribution과 model distribution 간의 discrepancy를 measure 하기 위해 Maximum Mean Discrepancy (MMD)를 활용

< Overall of SLED >

• Energy distance를 활용해 continuous latent space를 modeling 하는 speech language model
• 결과적으로 기존보다 우수한 성능을 달성

2. Maximum Mean Discrepancy and Generalized Energy Distance

• Integral probability metric은 $\mathbb{R}^{n}$ 상 probability distribution 간의 distance function에 해당함
  • $\mathbb{R}^{n}$의 real-valued function class $\mathcal{F}$가 주어졌을 때, integral probability metric은:
    (Eq. 1) $ D_{\mathcal{F}}(p,q)=\text{sup}_{f\in\mathcal{F}}\left[ \mathbb{E}_{x\sim p(x)}[f(x)]-\mathbb{E}_{y\sim q(y)}[f(y)]\right]$
    - $p,q$ : model, data distribution
    - BUT, function class $\mathcal{F}$의 richness로 인해 finite sample로 $D_{\mathcal{F}}(p,q)$를 estimate 하는 것은 impractical 함
  • 이때 Maximum Mean Discrepancy (MMD)는 function class $\mathcal{F}$를 reproducing kernel Hilbert space $\mathcal{H}$의 unit ball로 restrict 하여 estimation 문제를 해결함:
    (Eq. 2) $\text{MMD}(p,q)=\text{sup}_{||f||_{\mathcal{H}}\leq 1}\left[\mathbb{E}_{x\sim p(x)}[f(x)]-\mathbb{E}_{y\sim q(y)}[f(y)]\right]$
  • Real-valued function $k(x,y)$가 symmetric이고 positive-definite라고 가정하면 kernel $k$는 reproducing kernel Hilbert space $\mathcal{H}$를 정의함
    1. 그러면 해당 space 내의 모든 critic function $f\in \mathcal{H}$는 $f(x)=\langle f,k(x,\cdot)\rangle_{\mathcal{H}}$와 같이 express 됨
    2. 이를 probability distribution embedding으로 extend 하면 모든 $f\in \mathcal{H}$에 대해 $\mathbb{E}_{x\sim p(x)}[f(x)]=\langle f, \mu_{p}\rangle_{\mathcal{H}}$인 $\mu_{p}\in\mathcal{H}$를 정의할 수 있음
    3. 여기서 $\mu_{p}$의 existence condition이 만족되면 $\mu_{p}=\mathbb{E}_{x\sim p(x)}[k(x,\cdot)]$이고, MMD는 mean embedding 간의 distance로 express 될 수 있음:
       (Eq. 3) $\text{MMD}_{k}^{2}(p,q)=||\mu_{p}-\mu_{q}||^{2}_{\mathcal{H}}=\mathbb{E}_{x,x'\sim p \,\, y,y'\sim q}\left[k(x,x')+k(y,y')-2k(x,y)\right]$
       - $x,x', y,y'$ : $p,q$의 independent sample
  • $\mathcal{F}$의 어떤 choice에 대해서도 $D_{\mathcal{F}}$는 pseudometric에 해당하므로, metric의 property는 만족하지만 $p,q$가 identical 하지 않을 때 $D_{\mathcal{F}}(p,q)=0$이 될 수 있음
    1. BUT, mean embedding $\mu_{p}$가 injective일 때 $\text{MMD}(p,q)$는 metric이 되고, 이를 만족하는 kernel을 characteristic kernel이라고 함
    2. 결과적으로 characteristic kernel function $k(x,y)$를 select 하면 $\text{MMD}(p,q)$는 strictly proper scoring rule이 되고 implicit probabilistic generative model을 training 하는 데 사용할 수 있음
  • 한편으로 metric space $(\mathbb{R}^{n},d)$ 상의 두 probability distribution 간의 Generalized Energy Distance (GED)는:
    (Eq. 4) $\text{GED}^{2}_{d}(p,q)=\mathbb{E}_{x,x'\sim p\,\, y,y'\sim q}\left[2d(x,y)-d(x,x')-d(y,y')\right]$
    - 이때 distance function $d$가 negative type이거나 conditionally negative-definite이면 $\text{GED}^{2}(p,q)\leq 0$이고, distribution 간의 pseudometric을 구성함
  • 실제로 GED는 MMD의 special case로 볼 수 있고, $\mathbb{R}^{n}$ 위의 nondegenerate kernel $k$는 negative type의 valid semimetric $d$를 다음과 같이 정의함:
    (Eq. 5) $d(x,y)=k(x,x)+k(y,y)-2k(x,y)$
  • 그러면 negative type의 semimetric $d$는 적어도 하나 이상의 induced kernel을 통해 generate 됨:
    (Eq. 6) $k(x,y)=d(x,z)+d(y,z)-2d(x,y)$
    - $z$ : $\mathbb{R}^{n}$ 상의 임의의 point
  • $\text{GED}^{2}_{d}$는 $d$를 generate 하는 kernel $k$에 대한 $\text{MMD}^{2}_{k}$와 equivalent 함
    - 따라서 distance function $d$가 appropriately choice 되면 implicit generative model을 training 하는 criterion으로 사용할 수 있음

3. Method

- Language Modeling in Continuous Latent Space

• 논문에서는 speech waveform을 continuous representation sequence로 encoding 하고 해당 continuous latent space 내에서 autoregressive modeling을 수행함
  • 먼저 audio sample $x\in\mathbb{R}^{Tf}$가 주어지면 $h=\text{Enc}(x),\,\, h\in \mathbb{R}^{Tf_{h}\times n}$과 같이 continuous representation sequence로 encode 함
    - $T$ : audio duration, $f, f_{h}$ : 각각 audio waveform, latent sequence의 sample rate
  • 이때 model은 previously generated vector $h_{<t}$를 condition으로 continuous vector $h_{t}$의 distribution을 capture 하는 것을 목표로 함:
    (Eq. 7) $ p(h)=\prod_{t=0}^{Tf_{h}-1}p(h_{t}|h_{<t})$
  • Discrete domain에서 autoregressive model은 softmax function을 사용하여 각 step의 distribution을 vocabulary space 위에서 modeling 할 수 있음
  • 반면 continuous domain에서는 previous step을 condition으로 하여 각 step 마다 $\mathbb{R}^{n}$ space에서 distribution을 modeling 해야 함:
    (Eq. 8) $z_{t}=\psi(h_{<t};\theta),\,\,\hat{h}_{t}\sim p_{g}(h_{t}|z_{t};\phi)$
    - $\psi$ : autoregressive network, $g$ : $\mathbb{R}^{n}$ 상의 conditional generative module

Speech Language Modeling

- Per-token Generative Modeling via Energy Distance

• 논문은 각 step에서 conditional generative module $g$를 사용하여 continuous latent space에서 autoregressive modeling을 수행함
  • Model $g$는 autoregressive dependency를 incorporate 하는 condition representation $z_{t}$를 기반으로 current step $h_{t}$의 distribution을 modeling 함
  • 이때 model $g$는 speech modeling을 위해 다음을 만족해야 함:
    1. Modeling Capacity
       - $g$는 각 step에서 다양한 distribution을 효과적으로 capture 할 수 있어야 함
    2. Sampling Efficiency
       - $g$는 vocabulary에 대한 categorical sampling과 같이 high-sampling efficiency를 가져야 함
    3. Training Stability 
       - Conditional generative module $g$와 main autoregressive network $\psi$는 stable training algorithm으로 train 될 수 있어야 함
  • 위의 requirements를 따라 논문은 condition vector $z_{t}$와 noise vector $\epsilon$을 input으로 하여 continuous latent space $\mathbb{R}^{n}$으로 mapping하는 lightweight multi-layer perceptron $g$를 구성함:
    (Eq. 9) $ h_{t}=g(z_{t},\epsilon ;\phi)$
    - 이는 $\mathbb{R}^{n}$ 상에서 per-step distribution $p_{g}(h_{t}|z_{t})$를 implicitly define 함
  • Sampling process는 noise vector $\epsilon_{t}$를 sampling 하고, condition $z_{t}$와 함께 $g$를 통과시켜 수행됨
    1. 이때 network $g$에서는 AdaLN module을 사용해 condition vector $z_{t}$의 hidden state에 noise를 integrate 하여 randomness를 도입함
    2. $z_{t}$의 layer normalization module에서는 dimension-wise scale, shift parameter를 directly learning 하지 않고 sampling을 위한 random perturbation으로 취급함
       - Scale, shift는 input noise $\epsilon_{t}$에 linear transformation을 적용하여 얻어짐
  • Implicit conditional generative model $g$와 autoregressive network $\psi$를 simultaneously training 하기 위해 data, model 간의 distribution metric으로 MMD의 specialized form인 Energy Distance를 사용함
    1. Training은 simulated/ground-truth latent representation 간의 energy distance를 $g,\psi$의 parameter에 대해 minimizing 하는 것으로 수행됨
    2. 이때 data distribution은 optimization 시 fix 되어 있으므로 model parameter에 의존하지 않는 (Eq. 4)의 term은 discard 할 수 있음:
       (Eq. 10) $ \mathcal{L}_{GED}=\sum_{t}\mathbb{E}_{h_{t},h'_{t}}\left[2d(h_{t},h^{*}_{t})-d(h_{t},h'
       _{t})\right]$
       - $h^{*}$ : target latent waveform representation, $h_{t},h'_{t}$ : $p_{g}(h_{t}|z_{t})$의 independent sample
       
    3. $\mathcal{L}_{GED}$는 distance function $d$에 해당하는 kernel function이 characteristic인 경우 strictly proper scoring rule이 됨:
       (Eq. 11) $\mathcal{L}_{GED}=\sum_{t}\mathbb{E}_{h_{t},h'_{t}}\left[2||h_{t}-h^{*}_{t}||_{2}^{1} - ||h_{t}-h'_{t}||_{2}^{1}\right]$
       - 특히 $\beta\in(0,2)$일 때 $d(x,y)=||x-y||^{\beta}_{2}$가 해당 condition을 만족하므로, 논문은 $\beta=1$을 사용함
       - (Eq. 11)은 Root Mean Squared Error (RMSE)에 repulsive term $\mathbb{E}[|| h_{t}-h'_{t}||_{2}^{1}]$가 추가된 것으로 볼 수 있음
  • 한편으로 SLED는 continuous latent space에서 autoregressive modeling을 수행하므로 $\texttt{EOS}$ token을 predict 하여 언제 stop 할지를 결정할 수 없음
    1. 이를 해결하기 위해 논문은 MELLE를 따라 terminate를 결정하는 binary classification head를 도입함
    2. 구조적으로는 autoregressive output $z_{t}$를 scalar로 direct project 한 다음, sigmoid function을 적용하여 해당 step에서의 stop 여부를 결정함

- Classifier-Free Guidance

• Continuous latent generation은 discrete counterpart 보다 higher noise level을 가짐
  • 따라서 논문은 Classifier-Free Guidance (CFG)를 활용해 generation quality와 prompt alignment를 개선함
    1. 먼저 autoregressive generation의 각 step에서 $\psi$를 통한 additional forward pass를 수행하고, prompt text를 mask 하여 $z'_{t}$를 얻음
    2. $z_{t}, z'_{t}$를 linearly interpolate 하고 result를 per-token generative module $g$의 input으로 사용함:
       (Eq. 12) $ z_{t}^{cfg}=z'_{t}+\lambda(z_{t}-z'_{t}),\,\,\, h_{t}^{cfg}=g(z_{t}^{cfg},\epsilon;\phi)$
       - $\lambda$ : guidance strength ($\lambda=1.0$인 경우 naive conditional generation)
  • 추론 시에는 text prompt를 $0.1$의 probability를 randomly mask 함
    - $\texttt{EOT}$ token은 masking 중에도 preserve 되고 speech beginning token으로도 사용됨

- Streaming Inference

• SLED는 purely autoregressive model이므로 output을 refine 하는 post-processing module이 필요 없음
  • 특히 해당 property로 인해 SLED는 streaming generation이 가능함
    1. 즉, 각 autoregressive step에서 latent vector를 생성하고 이를 waveform synthesis에 바로 사용할 수 있음
    2. 이를 기반으로 논문은 full prompt text가 제공되기 전에 model이 generation을 수행하도록 함
  • 이때 EnCodec과 같은 audio codec은 streaming decoder를 가지고 있으므로 first-level streaming generation은 naturally supprot 됨
  • 따라서 논문은 incremental speech synthesis를 위해 autoregressive modeling 시 text, speech position의 order를 altering 함
    1. 먼저 text, speech position을 $n:m$ ratio로 interleave 함
       - 이는 $n$ text token마다 $m$ speech vector를 생성할 수 있도록 함
    2. $\texttt{EOT}$ token은 input text stream end를 indicate 하기 위해 사용됨
    3. Speech vector는 binary classification head가 stop decision을 내릴 때까지 autoregressively generate 됨
  • 논문은 model이 target vector를 생성하고 추론 시 generation이 필요한 input position에서 stop 하도록 training 함
    - 이때 interleaving ratio에 따라 next step이 text token인 경우 model은 filling token을 predict 할 필요가 없음
  • 추가적으로 streaming inference 역시 CFG를 적용하여 text stream이 masking을 요구할 때 model은 unconditional speech generation을 수행하도록 함
    - 이때 $\texttt{EOT}$는 beginning으로 사용됨

Streaming Inference

4. Experiments

- Settings

• Dataset : LibriHeavy
• Comparisons : MaskGCT, F5-TTS, Mega-TTS, VALL-E, VALL-E2, ELLA-V, CLaM-TTS, MELLE, FELLE, Llasa

- Results

• 전체적으로 SLED는 우수한 성능을 보임

Model 성능 비교

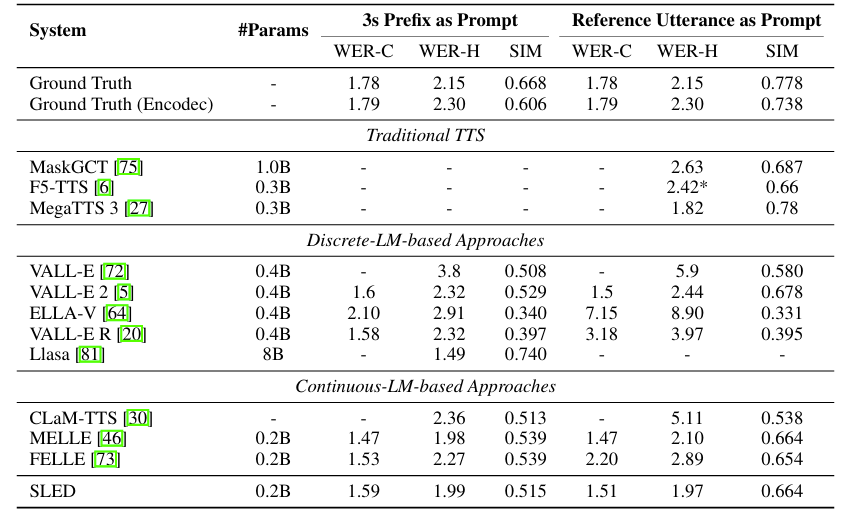
• Streaming inference에서도 안정적인 성능을 달성함

Streaming Inference

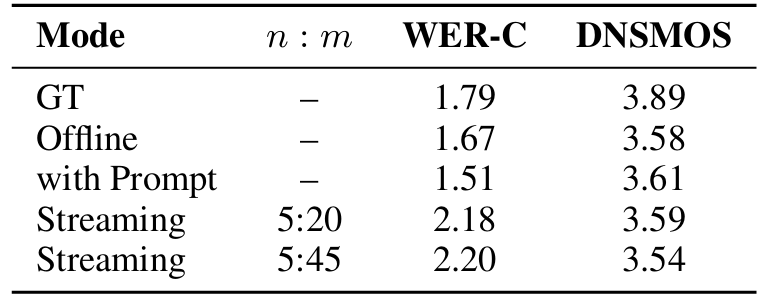
• Analysis
  • Energy distance를 사용하면 WER을 크게 향상할 수 있음

Energy Distance

• Guidance scale $\lambda=2.0$을 사용했을 때 최적의 결과를 달성할 수 있음

Classifier-Free Guidance

• DiTAR과 비교하여 SLED는 더 efficient 함

Decoding Efficiency