[Paper 리뷰] CLaM-TTS: Improving Neural Codec Language Modeling for Zero-Shot Text-to-Speech

CLaM-TTS: Improving Neural Codec Language Modeling for Zero-Shot Text-to-Speech

---

• Zero-shot Text-to-Speech를 위해 audio의 discrete token에 대한 multiple stream을 encode 하는 neural audio codec을 활용할 수 있음
• 이때 audio tokenization은 long sequence legnth와 multiple sequence modeling의 complexity로 인해 scalability의 한계가 있음
• CLaM-TTS
  • Token length에 대한 뛰어난 compression을 달성하고, Language model이 한 번에 multiple token을 생성할 수 있도록 하는 probabilistic residual vector quantization을 도입
  • 이를 통해 token stream 처리에 대한 cacaded modeling의 필요성을 제거
• 논문 (ICLR 2024) : Paper Link

---

1. Introduction

• 대규모 text data에 대해 training 된 Large Language Model (LLM)은 뛰어난 zero-shot learning capability를 보이고 있음
  • 이때 scaling paradigm은 LLM의 효율적인 training과 추론에 동시에 영향을 미침
    - 특히 discretized representation은 input length를 manageable size로 reduce 함으로써 해당 문제를 완화할 수 있음
  • 한편으로 speech domain에서 language modeling은 high-fidelity audio tokenization을 지원하는 neural audio codec을 활용하여 수행됨
    - 특히 zero-shot text-to-speech (TTS)를 위한 LLM으로써 우수한 성능을 보임
  • BUT, 해당 neural audio codec을 활용하여 TTS 모델을 scale up 하는 데는 여전히 어려움이 있음
    
    1. 기존 방식들은 주로 text와 audio token의 intermediary로써 self-supervised speech representation의 semantic token을 활용함
       
    2. 해당 semantic token은 audio token보다 information을 더 concisely compress 하지만 EnCodec과 같은 nerual codec은 5-second speech segment를 생성하기 위해 여전히 상당한 semantic token이 필요함
    3. 결과적으로 audio token modeling의 complexity 문제는 여전히 남아있음

-> 그래서 TTS에서 LLM의 효율적인 training과 추론을 지원하는 Codec Language Model-based TTS (CLaM-TTS)를 제안

 

• CLaM-TTS
  • Sequence 수에 따른 iterative modeling 없이 각 time step에 있는 모든 multiple token을 language model의 autoregressive step을 통해 생성
  • Probabilistic discrete representation learning을 활용하여 모든 discrete latent code가 training process에 participate 하도록 보장해 고품질 speech autoencoder를 구축
  • 추가적으로 latent language model이 한 번에 효율적으로 token stack을 생성할 수 있도록 하는 framework를 제공
    - Latent language model은 continuous latent audio representation을 생성하고 probabilistic quantization method를 사용해 discrete representation으로 변환

< Overall of CLaM-TTS >

• Latent language model을 통해 continuous latent audio representation을 생성하고 probabilistic quantization method를 사용해 효율적으로 discrete representation으로 변환
• 결과적으로 기존 방식들 보다 빠른 추론 속도를 가지면서 비교할만한 품질을 달성

2. Preliminaries

• 논문은 neural codec language modeling을 통해 zero-shot TTS 모델을 구축하는 것을 목표로 함
  • 이를 위해 text data $\mathbf{x}$와 해당 speech data의 mel-spectrogram representation $\mathbf{y}$의 2가지 data를 고려
  • 여기서 mel-spectrogram $\mathbf{y}$의 latent representation $\mathbf{z}_{1:T}$로 부터 $T$ discrete code seqeuence $\mathbf{c}_{1:T}:=\{\mathbf{c}_{1},...,\mathbf{c}_{T}\}$를 모델링
    - 이는 Residual Vector Quantization (RVQ)가 포함된 Variational AutoEncoder (VAE) framework를 통해 얻어짐
    - $\mathbf{c}_{t}$ : quantized, discrete code의 $D$-depth
  • 이후 text transcript $\mathbf{x}$에서 $\mathbf{c}_{1:T}$를 예측하는 것을 목표로 neural language model $p_{\theta}(\mathbf{c}_{1:T}| \mathbf{x})$를 적용
  • 추론 시 language model은 주어진 text $\mathbf{x}$에 대해 $\mathbf{c}_{1:T}$를 생성하고, 이후 VAE decoder와 pre-trained vocoder를 통해 음성으로 변환함

- Residual-Quantized Variational AutoEncoder (RQ-VAE)

• RQ-VAE는 residual vector quantization을 사용하여 data를 discrete code로 변환하는 neural network
  • RQ-VAE는 3가지 component로 구성됨:
    1. Data $\mathbf{y}$를 latent representation sequence $\mathbf{z}_{1:T}$로 mapping 하는 $\phi$로 parameterize 된 encoder
    2. 각 time $t$의 latent vector $\mathbf{z}_{t}$를 discrete code representation $\mathbf{c}_{t,1:D}=\mathrm{RQ}_{\psi}(\mathbf{z}_{t})$ 또는 quantized embedding $\hat{\mathbf{z}}_{t}$로 변환하는 residual vector quantizer $\mathrm{RQ}_{\psi}(\cdot)$
    3. Quantized latent representation sequence $\hat{\mathbf{z}}_{1:T}$로부터 data $\hat{\mathbf{y}}$를 reconstruction 하는 $\omega$로 parameterize 된 decoder
  • 여기서 $\mathbf{c}_{t,1:D}$는 set $\{c_{t,1},...,c_{t,D}\}$를 나타내고 $D$는 quantizer의 total depth를 나타낸다고 하자
    1. 그러면 encoder의 latent representation은 vocab size가 $V$인 codebook embedding에 대한 multi-stage nearest-neighbor lookup을 통해 quantize 됨
    2. 이는 codebook에서 각 depth $d$에 대해 residual error를 최소화하는 optimal code를 찾는 것으로 정의할 수 있음:
       (Eq. 1) $c_{t,d}=\arg\min_{c'\in\{1,...,V\}}|| \mathbf{r}_{t,d-1}-e_{\psi}(c';d)||^{2}, \,\, \mathbf{r}_{t,d}=\mathbf{r}_{t,d-1}-e_{\psi}(c_{t,d};d) \,\, \forall d\in[1,D]$
       - $\mathbf{r}_{t,0}=\mathbf{z}_{t}$, $e_{\psi}(c;d)$ : depth $d$에서 codebook의 $c$-th embedding vector
  • Embedding의 합 $\sum_{d=1}^{D}e_{\psi}(c_{t,d};d)$은 quantized latent representation $\hat{\mathbf{z}}_{t}$가 되고, 이는 decoder를 통해 input space로 convert back 됨
    - Codebook embedding은 exponential moving average update에 의해 cluster 된 latent로 update 됨

- Mean-Field Variational Inference

• $\psi$에 의해 parameterize 된 joint distribution $p_{\psi}(\mathbf{z}_{t},\mathbf{c}_{t,1:D})$로 characterize 된 latent variable model이 있다고 하자
  • 여기서 $\mathbf{z}_{t}$는 observed random variable이고, $\mathbf{c}_{t,1:D}$는 latent random variable set $\{\mathbf{c}_{t,1},...,\mathbf{c}_{t,D}\}$을 나타냄
  • 이때 variational inference는 approximate distribution $q(\mathbf{c}_{t,1:D}|\mathbf{z}_{t})$의 parameter에 대한 optimization 문제를 solving 하여 intractable distribution $p_{\psi}(\mathbf{c}_{t,1:D}|\mathbf{z}_{t})$을 근사하는 방법
    1. 대표적으로 Evidence Lower BOund (ELBO)와 같이 marginal log-likelihood $p_{\psi}(\mathbf{z}_{t})$에 대한 lower bound를 사용할 수 있음:
       $\log p_{\psi}(\mathbf{z}_{t})=\log \sum_{\mathbf{c}_{t,1:D}}p_{\psi}(\mathbf{z}_{t}|\mathbf{c}_{t,1:D})p(\mathbf{c}_{t,1:D})\geq \mathbb{E}_{q(\mathbf{c}_{t,1:D}|\mathbf{z}_{t})}\left[\log\frac{p_{\psi}(\mathbf{z}_{t}|\mathbf{c}_{t,1:D})p(\mathbf{c}_{t,1:D})}{q(\mathbf{c}_{t,1:D}|\mathbf{z}_{t})}\right]$
    2. 한편으로 mean-field variational inference는 obeserved variable $q(\mathbf{c}_{t,1:D}|\mathbf{z}_{t})=\prod_{d=1}^{D}q(\mathbf{c}_{t,d}|\mathbf{z}_{t})$에 따라 latent variable 간의 independence를 가정하는 variational inference 방식
    3. 이때 ELBO를 maximize 하는 각 optimal variational posterior distribution $q^{*}(\mathbf{c}_{t,d}|\mathbf{z}_{t})$은 다음을 만족함:
       (Eq. 2) $q^{*}(\mathbf{c}_{t,d}|\mathbf{z}_{t})\propto\exp\left(\mathbb{E}_{q(\mathbf{c}_{t,-d}|\mathbf{z}_{t})}\left[\log p_{\psi}(\mathbf{z}_{t}|\mathbf{z}_{t,d},\mathbf{z}_{t,-d})p(\mathbf{c}_{t,d},\mathbf{c}_{t,-d})\right]\right)$
       - $\mathbf{c}_{t,-d}$는 $\mathbf{c}_{t,d}$를 제외한 모든 depth $\mathbf{c}_{t,1:D}$의 latent variable
  • (Eq. 2)를 기반으로 iterative coordinate ascent algorithm을 적용하여 distribution $q$를 update 할 수 있음
    - Algorithm의 complexity는 $q(\mathbf{c}_{t,-d}|\mathbf{z}_{t})$에 대한 expectation 계산에 의해 결정됨

3. Method

- Mel-VAE

• CLaM-TTS는 short sequence length에서 discrete speech code를 생성하는 neural codec을 구축하는 것을 목표로 함
  • 이를 위해 아래 그림과 같이 speech audio의 mel-spectrogram을 compress 하는 RQ-VAE를 사용함
    - 이때 기존 vector quantization method의 codeword collapse 문제를 해결하기 위해, residual codeword를 학습하는 variational inference method를 도입
  • Mel-VAE는 앞선 RQ-VAE와 유사하게 구성됨
    1. 먼저 encoder는 mel-spectrogram $\mathbf{y}$를 latent representation sequence $\mathbf{z}_{1:T}$와 residual vector quantizer $\mathrm{RQ}_{\psi}(\cdot)$으로 mapping 하여,
    2. 각 time $t$의 latent vector $\mathbf{z}_{t}$를 discrete code representation $\mathbf{c}_{t}$나 해당 quantized embedding $\hat{\mathbf{z}}_{t}=\sum_{d=1}^{D}e_{\psi}(\mathbf{c}_{t,d};d)$으로 변환함
    3. Decoder는 quantized latent representation sequence $\hat{\mathbf{z}}_{1:T}$로 부터 mel-spectrogram $\hat{\mathbf{y}}$를 reconstruct 함
  • $q(\mathbf{c}_{t,1:D}|\mathbf{z}_{t})=\prod_{d=1}^{D}q(\mathbf{c}_{t,d}|\mathbf{z}_{t})$와 $p(\mathbf{c}_{t,d},\mathbf{c}_{t,-d})$가 uniformly distribute 되어 있다는 가정하에, mean-field variational inference는 다음의 distribution condition을 산출함:
    (Eq. 3) $q^{*}(\mathbf{c}_{t,d}|\mathbf{z}_{t})\propto\exp(\mathbb{E}_{q(\mathbf{c}_{t,-d}|\mathbf{z}_{t})}[\log p_{\psi}(\mathbf{z}_{t}|\mathbf{c}_{t,d},\mathbf{c}_{t,-d})])$
    - 이때 latent는 normal distribution $p_{\psi}(\mathbf{z}_{t}|\mathbf{c}_{t})=\mathcal{N}(\mathbf{z}_{t};\sum_{d}e_{\psi}(\mathbf{c}_{t,d};d),\sigma_{\psi}^{2}I)$을 따름
  • BUT, (Eq. 3)의 모든 depth에 대한 code의 interdependence는 iterative approach 없이 solve 하기 어려움
    1. 여기서 iterative coordinate update approach 대신 CLaM-TTS는 $\mathbb{E}_{q(\mathbf{c}_{t,-d}|\mathbf{z}_{t})}[\log p_{\psi}(\mathbf{z}_{t}|\mathbf{c}_{t,d},\mathbf{c}_{t,-d})]$를 모든 $d$에 대해 $\log p_{\psi}(\mathbf{z}_{t}|\mathbf{c}_{t,d},\mathbf{c}_{t,-d}^{*})$로 pointwise 하게 근사할 수 있음
       - $\mathbf{c}^{*}_{t,1:D}=\mathrm{RQ}_{\psi}(\mathbf{z}_{t})$
    2. 그러면 posterior는 $q^{*}(\mathbf{c}_{t,d}|\mathbf{z}_{t})\propto p_{\psi}(\mathbf{z}_{t}|\mathbf{c}_{t,d},\mathbf{c}^{*}_{t,-d})$로 나타남
  • 이를 기반으로 variational inference framework는 각 depth $d$의 codebook embedding을 independently optimize 함:
    (Eq. 4) $\mathcal{L}(\psi_{d};\mathbf{z}_{t},\mathbf{c}^{*}_{t,-d})=\mathbb{E}_{q^{*}(\mathbf{c}_{t,d}|\mathbf{z}_{t})}[-\log p_{\psi}(\mathbf{z}_{t}|\mathbf{c}_{t,d},\mathbf{c}^{*}_{t,-d})]$
    (Eq. 5) $\mathcal{L}(\psi;\mathbf{z}_{t},\mathbf{c}^{*}_{t,1:D})=\sum_{d=1}^{D}\mathcal{L}(\psi_{d};\mathbf{z}_{t},\mathbf{c}^{*}_{t,-d})$
  • Encoder parameter $\phi$, decoder parameter $\omega$에 대한 Mel-VAE의 다른 module은 commitment loss, reconstruction loss, adversarial loss로 train 됨:
    (Eq. 6) $\mathcal{L}(\omega,\phi;\mathbf{y},\mathbf{c}_{t,1:D})=\lambda_{r}|\mathbf{y}-\hat{\mathbf{y}}|+\lambda_{c}|| \mathbf{z}-\sum_{d}e_{\psi}(\mathbf{c}_{t,d};d)||^{2}+\lambda_{a}\mathcal{L}_{adv}$
    - $\lambda_{r}, \lambda_{c},\lambda_{a}$ : 각각 reconstruction loss, commitment loss, adversarial loss의 ocefficient
  • Adversarial training을 위해 CLaM-TTS는 multi-length discriminator, multi-resolution spectorgram discriminator를 채택
    - 그리고 least squares GAN objective와 $L1$ feature matching loss를 adversarial loss $\mathcal{L}_{adv}$로 사용

Overall of CLaM-TTS

- Latent Language Modeling

• 모델의 효율성을 향상하기 위해 text $\mathbf{x}$가 주어지는 conditional speech code language model을 구축함
  • 이는 speech code가 vector quantization을 통해 생성된다는 점을 활용
  • 따라서 vector 자체를 예측함으로써 residual vector quantization을 통해 각 layer에서 multiple token으로 변환할 수 있으므로, 기존의 sequential 한 speech code token 예측을 개선할 수 있음
    1. 구체적으로 논문은 text에서 token을 직접 예측하는 대신, residual vector quantization을 사용하여 speech code로 변환할 수 있는 speech의 continuous latent representation $\mathbf{z}_{t}$를 고려함:
       $p_{\theta}(\mathbf{c}_{1:T}|\mathbf{x})=\prod_{t=1}^{T}p_{\theta}(\mathbf{c}_{t}|\mathbf{x},\mathbf{c}_{<t})=\prod_{t=1}^{T}\int p_{\theta}(\mathbf{c}_{t},\mathbf{z}_{t}|\mathbf{x},\mathbf{c}_{<t})d\mathbf{z}_{t}=\prod_{t=1}^{T}\int p_{\theta}(\mathbf{z}_{t}|\mathbf{x},\mathbf{c}_{<t})p_{\psi}(\mathbf{c}_{t}|\mathbf{z}_{t})d\mathbf{z}_{t}$
       - 이때 $\mathbf{c}_{<t}$는 $\mathbf{c}_{1:t-1}$
       - $p_{\theta}(\mathbf{c}_{t}|\mathbf{z}_{t},\mathbf{x}, \mathbf{c}_{<t})$의 대체로 Mel-VAE와 함께 학습된 probabilistic quantizer distribution $p_{\psi}(\mathbf{c}_{t}|\mathbf{z}_{t})$를 사용
    2. Conditional distribution $p_{\theta}(\mathbf{z}_{t}|\mathbf{x},\mathbf{c}_{<t})$를 Gaussian mixture model로 정의하면:
       $p_{\theta}(\mathbf{z}_{t}|\mathbf{x},\mathbf{c}_{<t})=\sum_{k=1}^{K}p_{\theta}(k|\mathbf{x},\mathbf{c}_{<t})\mathcal{N}(\mathbf{z}_{t};\mu_{\theta}(k,\mathbf{x},\mathbf{c}_{<t}),\sigma_{\psi}^{2}I)$
    3. 위 모델로부터 log-likelihood에 대한 다음의 variational lower bound를 얻을 수 있음:
       $\log p_{\theta}(\mathbf{c}|\mathbf{x})\geq \sum_{t=1}^{T}\mathbf{E}_{q(k|\mathbf{x},\mathbf{c}_{\leq t})}\left[ -D_{KL}(p_{\psi}(\mathbf{z}_{t}|\mathbf{c}_{t})||p_{\theta}(\mathbf{z}_{t}|\mathbf{x},\mathbf{c}_{<t},k))+\log p_{\theta}(k|\mathbf{x},\mathbf{c}_{<t})+\mathcal{B}(\psi,\mathbf{c}_{t})\right]$
       $\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=-\mathcal{L}_{\text{VB}}(\theta)+\mathcal{B}(\psi,\mathbf{c}_{t})$
  • 결과적으로 latent language model을 training 하기 위한 total loss는: 
    $\mathcal{L}(\theta)=\mathcal{L}_{\text{VB}}(\theta)+\mathcal{L}_{\text{EOS}}(\theta)$
    - 이때 second loss $\mathcal{L}_{\text{EOS}}(\theta)$는 End of Speech $\text{EOS}$를 identify 하기 위한 binary classifier training을 위함
  • CLaM-TTS는 mixture weight, Gaussian mixture distribution의 평균, generation concluding probability를 output 하는 autoregressive latent model을 활용함
    1. 구조적으로는 transformer decoder와 3가지 parallel module을 통합하여 구성됨
       - $p_{\theta}(k|\mathbf{x},\mathbf{c}_{<t})$에 대한 softmax actiavtion을 사용하는 prediction layer
       - $\mu_{\theta}(k, \mathbf{x},\mathbf{c}_{<t})$에 대한 prediction layer
       - $\text{EOS}$ prediction을 위한 binary classifier layer
    2. 추가적으로 Mel-VAE의 pre-trained quantizer $\mathrm{RQ}_{\psi}(\cdot)$도 사용

- Model Architecture and Inference

• Model Architecture
  • Mel-VAE은 Denoising Diffusion Probabilistic Model (DDPM)의 causal 1D convolutional U-Net을 사용함
    - 이때 skip connection과 attention layer를 제거하고 1D ConvNeXt block을 decoder의 final layer에 추가
  • 추가적으로 각 depth에 대해 codebook size가 1024인 32-stage residual vector quantization을 사용
  • Text-to-Code latent language model의 경우, transformer-based encoder-decoer LM을 채택
    - 특히 SoundStorm과 유사하게 pre-trained ByT5-large를 활용하고 text encoder를 frozen 함
• Inference
  • Text-to-Code generation은 3단계로 진행됨
    1. 먼저 time step $t$에서 distribution $p_{\theta}(k|\mathbf{x},\mathbf{<t})$으로부터 $k$를 randomly select 함
    2. 다음으로 $p_{\theta}(\mathbf{z}_{t}|\mathbf{x},\mathbf{c}_{<t},k)$에서 latent vector $\mathbf{z}_{t}$를 random sampling 함
       - 즉, time step $t$에서 discrete code는 learned quantizer $\mathbf{c}_{t}=\mathrm{RQ}_{\psi}(\mathbf{z}_{t})$를 통해 얻어짐
    3. 이후 $\text{EOS}$의 probability가 0.5 이상이면 generation을 종료하고, 그렇지 않으면 step을 진행함
  • 결과적으로 생성된 code는 Mel-VAE decoder를 통해 mel-spectrogram으로 decoding 되고, pre-trained vocoder인 BigVGAN을 통해 raw waveform으로 최종 변환됨

4. Experiments

- Settings

• Dataset : 아래 표 참고 (11 language dataset) 
• Comparisons : YourTTS, VALL-E, Spear-TTS, VoiceBox

사용된 Dataset

- Results

• English-only continuation, cross-sentence task에 대해 CLaM-TTS는 VoiceBox와 비교할만한 성능을 보임

English-only Continuation 성능

English-only Cross-Sentence 성능

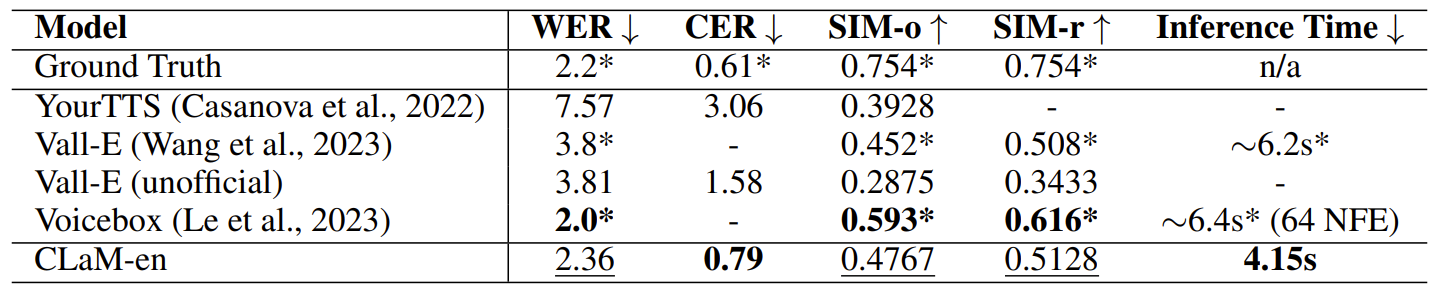
• 주관적 품질 비교에서도 CLaM-TTS는 가장 뛰어난 것으로 나타남

MOS 품질 비교

• 한편으로 Multi-lingual continuation 측면에서도 CLaM-TTS는 우수한 성능을 보임

Multi-lingual Continuation 성능

• Effectiveness of Proposed RVQ
  • Ablation study 측면에서 Mel-VAE에 적용된 RVQ의 효과를 확인해 보면, 논문에서 제안된 RVQ가 baseline RVQ보다 더 효과적인 것으로 나타남
  • 특히 CLaM-TTS의 RVQ는 EnCodec보다 뛰어난 speech reconstruction 성능을 보임 

제안된 RVQ의 효과