[Paper 리뷰] PALLE: Pseudo-Autoregressive Neural Codec Language Models for Efficient Zero-Shot Text-to-Speech Synthesis

PALLE: Pseudo-Autoregressive Neural Codec Language Models for Efficient Zero-Shot Text-to-Speech Synthesis

---

• Zero-Shot Text-to-Speech에서 autoregressive model은 generation speed, non-autoregressive model은 temporal modeling의 한계가 있음
• PALLE
  • Autoregressive의 explicit temporal modeling과 non-autoregressive의 parallel genertion을 combine 한 pseudo-autoregressive approach를 도입
  • Two-stage framework를 기반으로 first stage에서는 pseudo-autoregressive generation을 수행하고 second stage에서는 non-autoregressive refinement를 수행
• 논문 (MM 2025) : Paper Link

---

1. Introduction

• Zero-shot Text-to-Speech (TTS)는 Autoregressive (AR), Non-Autoregressive (NAR) model로 나눌 수 있음
  • 먼저 AR model은 previous output을 condition으로 하여 left-to-right로 speech를 생성함
    - AR model은 strong temporal grounding을 가진다는 장점이 있지만, step 별로 fix 된 prediction size로 인한 추론 속도의 문제가 있음
    
  • 한편으로 NAR model은 Diffusion, Generative Adversarial Network (GAN), Masked Generative Modeling 등을 활용하여 parallel generation을 지원함
    1. 특히 최근의 E2-TTS, F5-TTS는 phoneme-level duration prediction이나 explicit alignment supervision 없이도 text-to-speech alignment가 가능함
    2. BUT, 이러한 NAR model은 temporal modeling의 부족으로 인한 intelligibility의 한계가 있음

-> 그래서 zero-shot TTS에서 AR, NAR modeling의 한계를 개선한 PALLE를 제안

 

• PALLE
  • AR의 temporal modeling과 NAR의 parallel generation을 combine 한 Pseudo-Autoregressive (PAR) codec language modeling paradigm을 적용
    - 특히 pregressive commitment를 통해 span-level causal ordering을 enforce 하여 bidirectional masked generative Transformer에 temporal inductive bias를 도입함
  • 추가적으로 PAR 기반의 two-stage framework를 통해 TTS system을 구축

< Overall of PALLE >

• Codec language modeling을 위해 AR, NAR을 combine 한 zero-shot TTS model
• 결과적으로 기존보다 우수한 성능을 달성

2. Pseudo-Autoregressive Language Modeling

• 논문은 pseudo-Autoregressive (PAR) codec language modeling을 위해 NAR, AR modeling을 unify 함
  - PAR은 NAR의 parallel prediction과 AR의 temporal modeling을 combine 하여 speech의 temporal order를 따르면서 structured parallelism을 지원함

AR, NAR, PAR

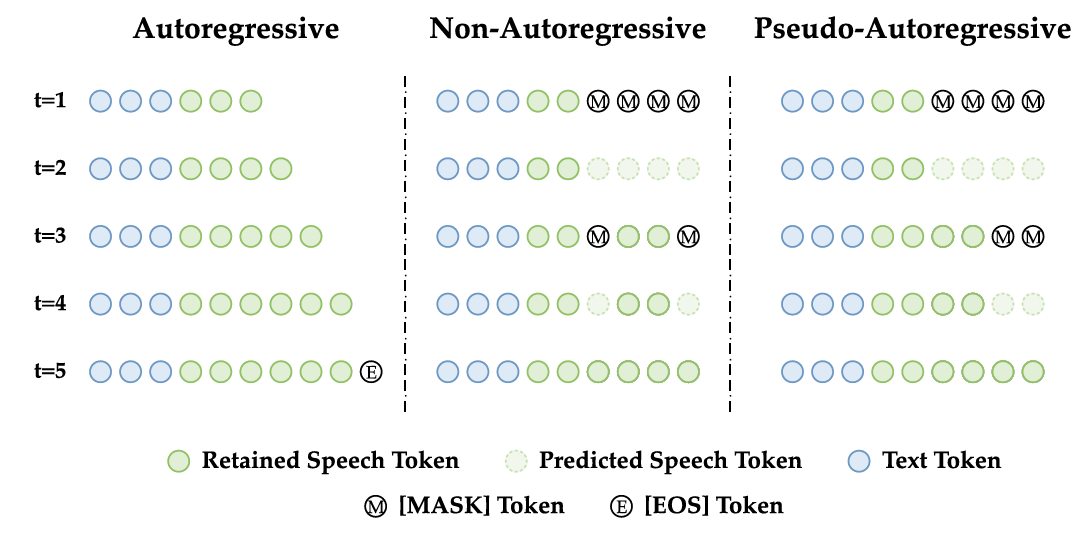
- Formulation

• Speech sample $\mathbf{y}$와 해당 tokenized text transcription $\mathbf{x}$가 주어진다고 하자
  • 그러면 pre-trained speech tokenizer는 speech sample을 $\mathbf{c}=\text{Encode}_{spch}(\mathbf{y})$와 같이 downsampled length $T$의 discrete speech token $\mathbf{c}$로 encoding 함
  • PAR model은 bidirectional masked generative Transformer를 기반으로 함
    1. Training 시에는 Cross-Entropy loss를 사용하여 text content $\mathbf{x}$에 condition 된 speech token $\mathbf{c}$의 likelihood를 maximize 함
    2. 이때 각 step 마다 random starting position에서 end까지 contiguous span에 mask가 적용됨:
       (Eq. 1) $ \mathbf{m}=[\underset{T-\ell}{\underbrace{0,0,...,0}}, \underset{\ell}{\underbrace{1,1,...,1}}]$
       - $\ell$ : masked span length
    3. 그러면 model은 length $k=\lfloor rT\rfloor$의 masked portion $\mathbf{m}\odot\mathbf{c}$의 leftmost span을 predict 하도록 optimize 됨
       - $r\in(0,1)$ : fixed ratio
    4. 해당 prediction은 unmasked protion $(1-\mathbf{m})\odot \mathbf{c}$와 text content $\mathbf{x}$로 condition 되고, 다음 objetive를 maximizing 하는 것과 같음:
       (Eq. 2) $\arg\max_{\theta} p\left([\mathbf{m}\odot \mathbf{c}]_{0:k}|(1-\mathbf{m})\odot \mathbf{c}, \mathbf{x};\theta\right)$
       - $[\cdot ]_{0:k}$ : first $k$ element, $\theta$ : model parameter
    5. Mask starting position은 training 중에 dynamically sampling 되어 model이 다양한 preceding speech context를 기반으로 time-dimension에서 next span을 predict 할 수 있도록 함
  • 추론 시 tokenized text $\mathbf{x}^{gen}$, unseen speaker의 speech prompt $\mathbf{y}^{ref}$, 해당 tokenized text $\mathbf{x}^{ref}$가 주어지면 length $T^{ref}$의 speech token $\mathbf{c}^{ref}=[c'_{0},c'_{1},...,c'_{T^{ref}-1}]$이 추출됨
    1. 이때 target speech token length $T^{gen}$은 arbitrarily determine 되거나 estimate 될 수 있고, 추론은 extended speech token sequence를 initialize 하여 시작됨:
       (Eq. 3) $\mathbf{c}_{(0)}^{ext}=[c'_{0},c'_{1},...,c'_{T^{ref}-1}, \underset{T^{gen}-T^{ref}}{\underbrace{0,0,...,0}}]$
       - Appended $0$은 generate 될 speech token의 placeholder로 사용됨
    2. 각 step $t$에서 모든 token은 parallel predict 되고 leftmost $k'=\min(\lfloor r'T^{gen}\rfloor, N_{left})$ token은 retain 됨
       - $r'\in (0,1)$ : fixed ratio, $N_{left}$ : generate 될 token 수
    3. Prediction은 text prompt $\mathbf{x}^{ref}$, target text $\mathbf{x}^{gen}$, current extended speech token sequence $\mathbf{c}_{(t)}^{ext}$로 condition 되고, binary mask는 다음과 같이 구성됨:
       (Eq. 4) $\mathbf{m}_{(t)}=[\underset{T^{ref}+t\times k'}{\underbrace{0,0,...,0}}, \underset{k'}{\underbrace{1,1,...,1}},0,0,...,0]$
       
    4. Extended speech token sequence는 다음의 iterative rule에 따라 update 됨:
       (Eq. 5) $\mathbf{c}_{(t+1)}^{ext}=(1-\mathbf{m}_{(t)})\odot \mathbf{c}_{(t)}^{ext} +\mathbf{m}_{(t)}\odot \arg\max_{\mathbf{c}_{(t+1)}^{ext}} p\left(\mathbf{c}_{(t+1)}^{ext}| \mathbf{c}_{(t)}^{ext}, \mathbf{x}^{ref},\mathbf{x}^{gen};\theta\right)$
       - First part는 speech prompt와 previously generated span을 포함하고, second part는 currently generated token을 포함함
       - 해당 generation과 selectively updating은 모든 token이 생성될 때까지 continue 됨
  • Final speech token $\mathbf{c}_{(\infty)}^{ext}$는 pre-trained speech detokenizer와 vocoder를 사용하여 $\hat{\mathbf{y}}=\text{Decode}_{spch}(\mathbf{c}_{(\infty)}^{ext})$와 같이 waveform $\hat{\mathbf{y}}$로 convert 됨

- Discussion

• PAR은 general language modeling paradigm으로 정의됨
  - 이는 MaskGCT의 temporal concatenation과 E2-TTS의 feature dimension cocatenation을 모두 accommodate 함

3. Method

- Architecture

• Text가 주어지면 BPE-based text tokenizer가 text를 subword token으로 convert 하고, shared architecture를 가지는 2개의 masked generative Transformer를 통해 해당 token을 process 함
  • First stage에서는 PAR model을 사용하여 speech token을 생성하고 second stage에서는 NAR model을 사용해 speech token을 refine 함
  • 이후 built-in vocoder를 가지는 speech detokenizer를 통해 refined speech token을 waveform으로 convert 함
• Masked Generative Language Model
  • PALLE는 backbone으로 masked generative Transformer를 채택함
  • 이때 model은 equal length를 가지는 padded tokenized text sequence와 masked speech token sequence를 input으로 사용함
    1. Text embedding은 ConvNeXtV2 block 통해 further process 되어 strong temporal modeling을 제공함
    2. 두 sequence 모두 learnable scaling factor와 dropout이 포함된 sinusoidal positional encoding이 add 되고, feature dimension에서 concatenate 된 다음 linear projection layer로 전달됨
    3. 이후 convolutional positional embedding이 projected feature에 add 되어 temporal structure를 encode 함
  • 최종적으로 resulting sequence는 full context에 attend 하는 bidirectional Transformer에 전달됨 
• Speech Tokenizer and Detokenizer
  • 논문은 CosyVoice2의 pre-trained S3Tokenizer를 사용하여 input waveform에서 25Hz rate로 discrete semantic token을 추출함
  • Mel-spectrogram reconstruction 역시 CosyVoice2의 pre-trained Conditional Flow Matching (CFM) model을 활용하여 discrete speech token으로부터 mel-spectrogram을 reconstruct 함
  • 최종적으로 생성된 mel-spectrogram은 pre-trained HiFi-GAN vocoder를 사용하여 waveform으로 convert 됨

Overview

- Training: Conditional Codec Masked Language Modeling

• Speech token sequence를 $\mathbf{c}=[c_{0},c_{1},...,c_{T-1}]$, length $L$의 tokenized transcript를 $\mathbf{x}=[x_{0},x_{1},...,x_{L}]$이라고 하자
• Stage 1
  • PALLE는 first stage에서 E2-TTS의 modality fusion method를 활용하여 PAR modeling을 구축함 
    1. 이때 text token sequence $\mathbf{x}$는 speech token sequence $\mathbf{c}$의 length에 match 하기 위해, $\text{[PAD]}$ filler token으로 padding 되어 embedding 이후의 feature dimension fusion을 지원함
    2. 그러면 padded text sequence $\mathbf{x}^{ext}$는:
       (Eq. 6) $ \mathbf{x}^{ext}=[x_{0},x_{1},...,x_{L-1},\underset{T-L}{\underbrace{ \text{[PAD]},\text{[PAD]},...,\text{[PAD]}}}]$
  • 각 step에서 $\mathbf{c}$ 내 speech token의 contiguous span은 binary mask $\mathbf{m}'$을 사용해 randomly mask 되고, starting position $s$는 uniform distribution에서 sampling 됨:
    (Eq. 7) $s\sim\mathcal{U}\left\{\lfloor 0.3T\rfloor,\lfloor 0.3T\rfloor +1,..., T-\lfloor 0.1T\rfloor -1\right\}$
  • 해당 $s$를 기반으로 binary mask $\mathbf{m}'$은 다음과 같이 정의됨:
    (Eq. 8) $\mathbf{m}'=[\underset{s}{\underbrace{0,0,...,0}},\underset{T-s}{\underbrace{1,1,...,1}}]$
  • Model은 masked speech token sequence에서 size $k=\lfloor 0.1T\rfloor$의 leftmost span $[\mathbf{m}'\odot \mathbf{c}]_{0:k}$를 predict 하도록 optimize 되고, unmasked portion $(1-\mathbf{m}')\odot \mathbf{c}$와 padded text sequence $\mathbf{x}^{ext}$로 condition 됨
  • 결과적으로 Stage 1의 training objective는:
    (Eq. 9) $\arg\max_{\theta} p\left([\mathbf{m}'\odot \mathbf{c}]_{0:k}|(1-\mathbf{m}')\odot \mathbf{c},\mathbf{x}^{ext};\theta\right)$
• Stage 2
  • Stage 1과 마찬가지로 $\mathbf{x}$는 speech token sequence $\mathbf{c}$의 length에 match 하기 위해 filler token $\text{[PAD]}$로 padding 됨 
  • $\lfloor 0.3T\rfloor$ 이상의 speech token은 probability $p=0.1$로 independently mask 되어 binary mask $\mathbf{m}''=\{0\}^{\lfloor 0.3T\rfloor}\oplus \{0,1\}^{T-\lfloor 0.3T\rfloor}$를 생성함
    - $\oplus$ : concatenation, $1$ : masked position
  • 그러면 model은 masked speech token $\mathbf{m}''\odot \mathbf{c}$를 predict 하도록 optimize 되고, unmasked speech token $(1-\mathbf{m}'')\odot \mathbf{c}$와 padded text token sequence $\mathbf{x}^{ext}$로 condition 되어 다음의 objective를 maximize 함:
    (Eq. 10) $\arg\max_{\theta}p\left(\mathbf{m}''\odot \mathbf{c}|(1-\mathbf{m}'')\mathbf{c}, \mathbf{x}^{ext};\theta\right)$

Two-Stage Framework

- Inference: In-Context Learning via Prompting

• Length $L^{gen}$의 tokenized text를 $\mathbf{x}^{gen}=[x_{0}^{g},x_{1}^{g},...,x_{L_{gen}-1}^{g}]$, speech prompt를 $\mathbf{y}^{ref}$, length $L^{ref}$의 tokenized text prompt를 $\mathbf{x}^{ref}=[x_{0}^{r},x_{1}^{r},...,x_{L^{ref}-1}^{r}]$, $\mathbf{y}^{ref}$에 대한 length $T^{ref}$의 speech token을 $\mathbf{c}^{ref}=[c_{0}^{r},c_{1}^{r},...,c_{T^{ref}-1}^{r}]$이라고 하자
• Stage 1
  • Target speech token length $T^{gen}$은 pre-define 되거나 linearly estimate 됨:
    (Eq. 11) $ T^{gen}=T^{ref}\times \left(1+\frac{L^{gen}}{L^{ref}}\right)$
    
  • Prompt speech token sequence $\mathbf{c}^{ref}$는 $T^{gen}$에 match 하기 위해 $\text{[MASK]}$ token으로 masking 됨:
    (Eq. 12) $\mathbf{c}^{ext}=[c_{0}^{r},c_{1}^{r},...,c_{T^{ref}-1}^{r},\underset{T^{gen}-T^{ref}}{\underbrace{ \text{[MASK]},\text{[MASK]},...,\text{[MASK]}}}]$
  • Tokenized text sequence $\mathbf{x}^{ref}, \mathbf{x}^{gen}$은 concatenate 된 다음, $T^{gen}$에 reach 할 때까지 filter token $\text{[PAD]}$로 padding 됨:
    (Eq. 13) $\mathbf{x}^{ext}=[x_{0}^{r},...,x_{L^{ref}-1}^{r},x_{0}^{g},...,x_{L^{gen}-1}^{g}, \underset{T^{gen}-(L^{ref}+L^{gen})}{\underbrace{\text{[PAD]},...,\text{[PAD]}}}]$
  • Model은 time dimension에 따라 speech token을 progressively generate 함
    1. 각 step $t$에서는 모든 token을 parallel predict 하고 size $k'=\min(\lfloor r'T\rfloor, N_{left})$의 leftmost span만 retain 함
       - $r'\in (0,1)$ : fixed ratio, $N_{left}$ : 아직 생성되지 않은 token 수
    2. Prediction은 current extended speech/text token sequence인 $c_{(t)}^{ext}$와 $\mathbf{x}^{ext}$로 condition 됨
    3. Binary mask $\mathbf{m}_{(t)}$는 (Eq. 4), extended speech token sequence는 (Eq. 5)와 같이 iteratively update 됨:
       (Eq. 14) $\mathbf{c}_{(t+1)}^{ext}=(1-\mathbf{m}_{(t)})\odot\mathbf{c}_{(t)}^{ext}+ \mathbf{m}_{(t)}\odot \arg\max_{\mathbf{c}_{(t+1)}^{ext}}p\left( \mathbf{c}_{(t+1)}^{ext}| \mathbf{c}_{(t)}^{ext},\mathbf{x}^{ext};\theta\right)$
• Stage 2
  • Stage 2에서는 Stage 1에서 생성된 initial generation $\mathbf{c}_{(0)}^{'ext}=\mathbf{c}_{(\infty)}^{ext}$에 대해 low-confidence token을 re-masking/re-predicting 하는 방식으로 iteratively refine 함
  • 각 step $t$에서 model은 probability matrix $\mathbf{P}_{(t)}$를 생성함
    1. 이때 entry $P_{(t),n}$은 $\mathbf{c}_{(t)}^{ext}, \mathbf{x}^{ext}$로 condition 되어 $N$ speech token class의 class $n$에 대한 predicted probability를 나타냄:
       (Eq. 15) $ \mathbf{P}_{(t)}=p\left(\mathbf{c}^{'ext}_{(t+1)}|\mathbf{c}_{(t)}^{'ext},\mathbf{x}^{ext} ;\theta\right)\in\mathbb{R}^{T^{gen}\times N}$
    2. Confidence score matrix $\mathbf{C}_{(t)}\in\mathbb{R}^{T^{gen}}$은 해당 distribution의 negative min-entropy로 정의됨:
       (Eq. 16) $\mathbf{C}_{(t)}=\log \mathbf{P}_{(t)}^{max}[:,n]$
       - $\mathbf{P}^{max}_{(t)}$ : predicted distribution의 maximum probability
  • 논문은 confidence score를 rank 하고 pre-defined quantile $\gamma$를 사용하여 re-masking 할 lowest confidence token을 select 함
    1. Binary mask는 $\mathbf{m}_{(t)}\in\{0,1\}^{T^{gen}}$와 같고, 여기서 $1$은 masking position을 나타냄
    2. Extended speech token sequence $\mathbf{c}_{(t)}^{'ext}$는 (Eq. 14)와 같이 iteratively update 됨
       - 이때 same position에 대한 repeated refinement를 방지하기 위해 updated token의 confidence score는 $1$로 permanently setting 됨
  • 최종적으로 final speech token $\mathbf{c}_{(\infty)}^{ext}$는 waveform $\hat{\mathbf{y}}$로 convert 됨

4. Experiments

- Settings

• Dataset : LibriTTS
• Comparisons : VALL-E, E2-TTS, F5-TTS, MaskGCT, CosyVoice, CosyVoice2

- Results

• 전체적으로 PALLE의 성능이 가장 뛰어남

Model 성능 비교

• MOS 측면에서도 PALLE가 가장 우수한 성능을 보임

Subjective Evaluation

• Pseudo-Autoregressive vs. Autoregressive/Non-Autoregressive
  • PAR+NAR을 사용했을 때 최적의 성능을 달성함

PAR vs. AR/NAR

• Ablation Study
  • $0.9\times$에서 $1.3\times$ 사이의 duration multiplier를 사용했을 때 최적의 성능을 달성함

Duration Multiplier

• Inference step이 클수록 더 나은 성능을 얻을 수 있음

Inference Step 별 성능