[Paper 리뷰] VALL-E2: Neural Codec Language Models are Human Parity Zero-Shot Text to Speech Synthesizers

VALL-E2: Neural Codec Language Models are Human Parity Zero-Shot Text to Speech Synthesizers

---

• 기존의 VALL-E를 추가적으로 개선할 수 있음
• VALL-E2
  • Repetition Aware Sampling을 통해 기존 nucleus sampling process를 향상
  • Grouped Code Modeling을 통해 inference speed와 long sequence modeling을 개선
• 논문 (Microsoft 2025) : Paper Link

---

1. Introduction

• Text-to-Speech (TTS)는 text input으로부터 high clarity, intelligibility를 가진 high-quality speech를 생성하는 것을 목표로 함
  • 이때 unseen speaker에 대한 speech를 생성하려면 NaturalSpeech와 같이 zero-shot TTS를 수행해야 함
  • 특히 VALL-E는 3s의 recording 만으로 우수한 zero-shot TTS 성능을 달성함
    1. 구조적으로는 speech signal을 discrete codec code로 represent 하는 neural audio codec model에 해당함
    2. Coarse codec code를 생성하기 위해 Autoregressive (AR) model을 활용하고, fine codec code를 생성하기 위해 Non-Autoregressive (NAR) model을 활용함
  • BUT, VALL-E는 다음의 문제점이 있음:
    1. Stability : 추론 시 random sampling으로 인해 small top-$p$ value에 대해 infinite loop 문제가 발생함
       - ELLA-V와 같이 text-speech alignment information을 활용하면 이를 개선할 수 있지만 architecture가 복잡해지고 data scaling이 어려움
    2. Efficiency : audio codec model에 bound 되어 있어 추론 속도가 느림
       - SoundStorm, VoiceBox와 같이 fully NAR model을 활용할 수 있지만, naturalness 측면에서 한계가 있음

Human Parity Performance

-> 그래서 기존 VALL-E의 문제점을 개선한 VALL-E2를 제안

 

• VALL-E2
  • 기존 VALL-E의 random sampling 대신 Repetition Aware Sampling을 도입하여 decoding stability를 향상
  • Grouped Code Modeling을 활용하여 추론 속도를 향상하고 long context modeling 문제를 mitigate

< Overall of VALL-E2 >

• Repetition Aware Sampling, Grouped Code Modeling을 통해 VALL-E를 개선한 zero-shot TTS language model
• 결과적으로 human parity 성능을 달성

2. Method

- Problem Formulation: Grouped Codec Language Modeling

• VALL-E를 따라 논문은 speech signal을 discrete codec code로 represent 하기 위해 neural audio codec model을 활용하고, TTS를 conditional codec language modeling task로 취급함
  • Efficiency를 향상하기 위해, VALL-E2는 Grouped Codec Language Modeling을 채택하여 codec code sequence를 certain size의 group으로 partition 하고 각 codec code group을 하나의 frame으로 modeling 함
    - 이를 통해 audio codec model의 frame-rate constraint를 제거하고 frame-rate를 정수배로 reduce 할 수 있음
  • TTS training objective에 대해, VALL-E2는 text condition이 주어졌을 때 grouped code sequence의 likelihood를 maximize 하도록 optimize 됨
    1. 먼저 text sequence length $L$에 대해 audio sample $\mathbf{y}$와 해당 tokenized text transcription $\mathbf{x}=[x_{0},x_{1},...,x_{(L-1)}]$이 주어진다고 하자
    2. 그러면 pre-trained audio codec을 사용하여 audio sample $\mathbf{y}$를 codec code sequence $\mathbf{C}^{T\times J}=[\mathbf{c}_{0},\mathbf{c}_{1},...,\mathbf{c}_{(T-1)}]$로 convert 함
       - $J=8$ : codec model의 quantizer 수, $T$ : code sequence length, $\mathbf{c}_{t}$ : 각 time step의 $8$개 code
    3. 이후 group size $G$로 grouped code sequence $\mathbf{C}^{G}=[\mathbf{C}_{0:G},\mathbf{C}_{G:2G}, ...,\mathbf{C}_{(T-G):T}]$로 partition 함
       - $\mathbf{C}_{0:G}$ : group $[\mathbf{c}_{0},\mathbf{c}_{1},...,\mathbf{c}_{(G-1)}]$
       - 이때 일반적으로 utterance start에는 short silence가 존재하므로 code sequence length $T$가 group size의 정수배가 되도록 code sequence start에서 few code를 clip 함
    4. 최종적으로 VALL-E2 model $\theta$를 training 하여 text sequence $\mathbf{x}$에 condition 된 grouped code sequence $\mathbf{C}^{G}$의 negative log-likelihood를 minimize 함:
       (Eq. 1) $ \mathcal{L}=-\log p\left(\mathbf{C}^{G}|\mathbf{x};\theta\right)$
       (Eq. 2) $\,\,\,\,\,\, =-\sum_{t=0}^{T/G-1}\log p\left(\mathbf{C}_{t\cdot G:(t+1)\cdot G}|\mathbf{C}_{<t\cdot G},\mathbf{x};\theta \right)$
       - $\mathbf{C}_{t\cdot G:(t+1)\cdot G}$ : codec code $[\mathbf{c}_{t\cdot G},...,\mathbf{c}_{((t+1)\cdot G-1)}]$의 $t$-th group
       - $\mathbf{C}_{<t\cdot G}$ : previous $(t-1)$ group의 all codec code
  • 추론 시 VALL-E2는 prompt를 통해 zero-shot TTS를 수행함
    1. 먼저 text sequence $\mathbf{x}$와 unseen speaker의 enrolled speech sample $\mathbf{y}'$이 주어지면, grouped code sequence $\mathbf{C}^{P}=\mathbf{C}^{G}_{<T'}=[\mathbf{C}_{0:G},\mathbf{C}_{G:2G},...,\mathbf{C}_{(T'-G):T'}]$을 얻을 수 있음 
    2. 이후 text sequence $\mathbf{x}$와 code prompt $\mathbf{C}^{P}$에 condition 된 target grouped code sequnce $\mathbf{C}^{T}=\mathbf{C}_{\geq T'}^{G}=[\mathbf{C}_{T':(T'+G)},...,\mathbf{C}_{(T-G):T}]$를 생성함:
       (Eq. 3) $\mathbf{C}^{T}=\arg\max_{\mathbf{C}} p\left(\mathbf{C}|\mathbf{C}^{P}, \mathbf{x};\theta\right)$
       (Eq. 4) $\,\,\,\,\,\,\,\,\,\, =\arg\max_{\mathbf{C}}\sum_{t=T'/G}^{T/G-1}\log p\left(\mathbf{C}_{t\cdot G:(t+1)\cdot G}|\mathbf{C}_{<t\cdot G},\mathbf{x};\theta \right)$
       
    3. 최종적으로 neural codec decoder는 target code sequence $\mathbf{C}^{T}$를 target speech waveform으로 convert 함

- VALL-E2 Architecture

• VALL-E2는 Autoregressive (AR) codec language model과 Non-Autoregressive (NAR) codec language model을 사용하는 hierarchical structure를 기반으로 구성됨
  • AR model은 autoregressive manner로 각 frame에 대한 first codec code sequence를 생성하고 NAR model은 preceding code sequence를 기반으로 remaining code sequence를 non-autoregressive manner로 생성함
  • 구조적으로는 text embedding layer, code embedding layer, code prediction layer를 포함한 Transformer architecture를 활용함
    1. 이때 서로 다른 codec quantizer의 code에 대해 distinct embedding을 사용하고, code prediction layer의 parameter를 code embedding layer의 parameter와 share 함
    2. 추가적으로 AR model에 group embedding layer를 추가하여 code embedding을 group embedding으로 project 하고, group 내의 code prediction을 위해 group prediction layer를 도입함
    3. NAR model에서는 predict code sequence ID를 specify 하기 위한 code ID embedding layer를 사용함
  • AR, NAR model은 서로 다른 attention mask strategy를 가짐
    - AR model은 causal attention을 사용하고, NAR model은 full attention을 사용함

- VALL-E2 Training

• VALL-E2 training에는 simple utterance-wise speech-transcription pair data만 필요함
  - 이때 training dataset의 audio, transcription에 대해 audio codec encoder와 text tokenizer를 사용하여 codec code $\mathbf{C}=[\mathbf{c}_{0},\mathbf{c}_{1},...,\mathbf{c}_{(T-1)}]$과 text sequence $\mathbf{x}=[x_{0},x_{1},...,x_{(L-1)}]$을 얻음
• Autoregressive Model Training
  • AR model은 text sequence $\mathbf{x}$를 condition으로 하여 autoregressive manner로 first codec code sequence $\mathbf{c}_{:,0}=[c_{0,0},c_{1,0},...,c_{(T-1),0}]$을 predict 하도록 training 됨
  • 먼저 text embedding sequence $\mathbf{E}^{x}=[\mathbf{e}_{0}^{x},\mathbf{e}^{x}_{1},...,\mathbf{e}^{x}_{(L-1)}]$과 code embedding sequence $\mathbf{E}^{c}=[\mathbf{e}^{c}_{0},\mathbf{e}^{c}_{1},...,\mathbf{e}^{c}_{(T-1)}]$를 text embedding matrix $\mathbf{W}^{x}$, code embedding matrix $\mathbf{W}^{c}$를 통해 얻음:
    (Eq. 5) $\mathbf{e}^{x}_{l}=\mathbf{W}^{x}\odot x_{l}$
    (Eq. 6) $\mathbf{e}^{c}_{t}=\mathbf{W}^{c}\odot c_{t,0}$
    - $l, t$ : text sequence, code sequence의 item index, $\odot$ : index selection 
  • 이후 code embedding sequence를 size $G$의 group으로 partition 하고 hidden dimension에서 각 code embedding group을 concatenate 한 다음,
  • Group embedding matrix $\mathbf{W}^{g}$를 사용하여 group embedding sequence $\mathbf{E}^{g}=[\mathbf{e}^{g}_{0},\mathbf{e}^{g}_{1},...,\mathbf{e}^{g}_{(T/G-1)}]$을 얻음:
    (Eq. 7) $\mathbf{e}_{t}^{g}=\mathbf{e}_{t\cdot G:(t+1)\cdot G}^{c}\cdot \mathbf{W}^{g}$
  • Text embedding sequence $\mathbf{E}^{x}$와 group embedding sequence $\mathbf{E}^{g}$를 concatenate 하고 사이에 special token $\text{<eos>},\text{<bos>}$를 insert 함:
    (Eq. 8) $\mathbf{E}^{0}=\mathbf{E}^{x}||\left[\mathbf{e}_{\text{<eos>}}, \mathbf{e}_{\text{<bos>}}\right]||\mathbf{E}^{g}$
    - $||$ : temporal dimension에서의 concatenation
  • 이후 learnable position embedding을 text embedding sequence와 group embedding sequence에 추가함
    1. AR model은 $\mathbf{E}^{0}$를 input으로 하여 special token $\text{<eos>}$가 end에 append 된 code sequence를 predict 하도록 training 됨
       - 이를 위해 linear mapping group prediction layer와 softmax code prediction layer를 사용함
    2. 이때 causal attention mask로 인해 각 code group $\mathbf{c}_{t\cdot G:(t+1)\cdot G, 0}$은 text sequence $\mathbf{x}$와 previous code $\mathbf{c}_{<t\cdot G,0}$에만 attend 함
  • 결과적으로 AR model parameter $\theta_{AR}$은 text sequence $\mathbf{x}$를 condition으로 first code sequence $\mathbf{c}_{:,0}$의 negative log-likelihood를 minimize 하여 optimize 됨:
    (Eq. 9) $\mathcal{L}_{AR}=-\log p(\mathbf{c}_{:,0}|\mathbf{x};\theta_{AR})$
    (Eq. 10) $\,\,\,\,\,\,\,\,\, =-\sum_{t=0}^{T/G-1}\log p\left(\mathbf{c}_{t\cdot G:(t+1)\cdot G, 0}|\mathbf{c}_{<t\cdot G,0},\mathbf{x};\theta_{AR}\right)$
    (Eq. 11) $\,\,\,\,\,\,\,\,\, =-\sum_{t=0}^{T/G-1}\sum_{t'=t\cdot G}^{(t+1)\cdot G-1}\log p\left(c_{t',0}| \mathbf{c}_{<t\cdot G, 0},\mathbf{x};\theta_{AR}\right)$
    - VALL-E2의 AR model에서 group sequence $\mathbf{c}_{:,0}=[\mathbf{c}_{0:G},\mathbf{c}_{G:2G,0},...,\mathbf{c}_{(T-G):T,0}]$은 autoregressive approach로 modeling 됨
    - 각 group $\mathbf{c}_{t\cdot G:(t+1)\cdot G,0}=[c_{t\cdot G,0},c_{(t\cdot G+1),0},...,c_{((t+1)\cdot G-1),0}]$은 non-autoregressive way로 modeling 됨
• Non-Autoregressive Model Training
  • First code sequence가 주어지면, NAR model은 text sequence $\mathbf{x}$와 preceding code sequence $\mathbf{c}_{:,<j}$를 condition으로 각 codec code ID $j$에 대해 remaining code sequence $\mathbf{c}_{:,j}$를 non-autoregressive manner로 생성하도록 training 됨
    - $j\in [1,...,7]$
  • 추론 시에는 prompt의 모든 8개 code sequence에 access 할 수 있으므로, training 시에는 모든 code sequence $\mathbf{C}$를 acoustic condition $\mathbf{C}_{<T'}$와 target code sequence $\mathbf{C}_{\geq T'}$으로 explicitly split 함
    - 여기서 length $T'$은 randomly sample 됨
  • 이후 model은 text sequence $\mathbf{x}$, acoustic condition $\mathbf{C}_{<T'}$의 모든 $J=8$ code sequence, preceding target code sequence $\mathbf{C}_{\geq T',<j}$를 기반으로 하여
    - Non-autoregressive manner로 각 target code sequence $\mathbf{c}_{\geq T',j}$를 predict 하도록 optimize 됨
  • 먼저 논문은 (Eq. 5)와 같이 text embedding matrix $\mathbf{W}^{x}$를 사용하여 text embedding sequence sequence $\mathbf{E}^{x}=[\mathbf{e}^{x}_{0},\mathbf{e}^{x}_{1},...,\mathbf{e}^{x}_{(L-1)}]$를 얻음
    1. 다음으로 code embedding matrix $\mathbf{W}^{c}$를 사용하여 acoustic condition $\mathbf{C}_{<T'}$과 target code sequence $\mathbf{C}_{\geq T',<j}$에서 code embedding sequence $\mathbf{E}^{c}=[\mathbf{e}_{0}^{c},\mathbf{e}_{1}^{c},...,\mathbf{e}_{(T-1)}^{c}]$를 얻고, code ID dimension에 따라 summing 함:
       (Eq. 12) $\mathbf{e}_{t}^{c}=\left\{\begin{matrix}
       \sum_{k=0}^{7}\mathbf{W}^{c}\odot c_{t,k}, & t<T' \\
       \sum_{k=0}^{j-1}\mathbf{W}^{c}\odot c_{t,k}, & t\geq T' \\
       \end{matrix}\right.$
       - $t$ : time step, $j$ : codec code ID
    2. 이후 code ID embedding matrix $\mathbf{W}^{id}$를 사용하여 codec code ID embedding $\mathbf{e}^{j}$를 얻음:
       (Eq. 13) $\mathbf{e}^{j}=\mathbf{W}^{id}\odot j$
    3. Text embedding sequence $\mathbf{E}^{x}$, code embedding sequence $\mathbf{E}^{c}$, codec code ID embedding $\mathbf{e}^{j}$를 concatenate 하고, special token $\text{<eos>}$를 중간에 insert함:
       (Eq. 14) $\mathbf{E}^{j}=\mathbf{E}^{x}||\left[\mathbf{e}_{\text{<eos>}}\right] ||\mathbf{E}^{c} ||\left[\mathbf{e}_{\text{<eos>}}\right] ||\left[\mathbf{e}^{j}\right]$
       - 이때 AR model과 마찬가지로 learnable position embedding을 text embedding sequence와 code embedding sequence에 add 함
    4. 결과적으로 NAR model은 $\mathbf{E}^{j}$를 전달받아 code prediction layer를 사용하여 각 code ID $j$에 해당하는 code sequence $\mathbf{c}_{:,j}$를 predict 하도록 training 됨
       - 이때 full attention mask를 사용하여 각 token $c_{t,j}$의 prediction은 entire input sequence에 attend 함
  • NAR model은 text sequence $\mathbf{x}$, acoustic condition $\mathbf{C}_{<T'}$의 모든 code sequence, preceding $j$ target code sequence $\mathbf{c}_{\geq T',<j}$를 condition으로 하여,
    • 각 $j$-th target code sequence $\mathbf{c}_{\geq T',j}$의 negative log-likelihood를 minimize 하도록 optimize 됨:
      (Eq. 15) $\mathcal{L}_{NAR}=-\log p\left( \mathbf{C}_{\geq T',\geq 1}|\mathbf{x}, \mathbf{C}_{<T',0};\theta_{NAR}\right)$
      (Eq. 16) $\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, =-\sum_{j=1}^{7}\log p\left(\mathbf{c}_{\geq T',j}|\mathbf{x},\mathbf{C}_{<T'},\mathbf{C}_{\geq T',<j};\theta_{NAR}\right)$
      
    • Training의 computational efficiency를 위해, 모든 $j$ value에 iterating 하여 loss를 calculate 하는 대신 $j\in[1,...,7]$을 randomly select 하여 loss를 통해 optimize 함:
      (Eq. 17) $\mathcal{L}_{NAR\text{_}j}=-\log p\left(\mathbf{c}_{\geq T',j}|\mathbf{x}, \mathbf{C}_{<T'},\mathbf{C}_{\geq T',<j};\theta_{NAR}\right)$

Training Overview

- VALL-E2 Inference

• 추론 시에는 prompt를 사용하여 zero-shot TTS를 수행함
  • Text sentence와 unseen speaker의 enrolled speech sample, 해당 transcription이 주어진다고 하자
    1. 먼저 speech transcription과 text sentence를 concatenate하고 text sequence $\mathbf{x}$를 text tokenizer를 통해 encoding 하여 text condition으로 사용함
    2. Speech sample은 audio codec encoder를 통해 code $\mathbf{C}^{P}=\mathbf{C}_{<T'}=[\mathbf{c}_{0},\mathbf{c}_{1},...,\mathbf{c}_{(T'-1)}]$로 convert 되어 prompt로 사용됨
  • 이후 conditional language model을 prompting 하여 AR, NAR model을 통해 target code $\mathbf{C}_{\geq T'}=[\mathbf{c}_{T'},...,\mathbf{c}_{(T-1)}]$을 생성함
  • 최종적으로 target code는 audio codec decoder를 통해 target speech signal로 synthesize 됨

Inference Overview

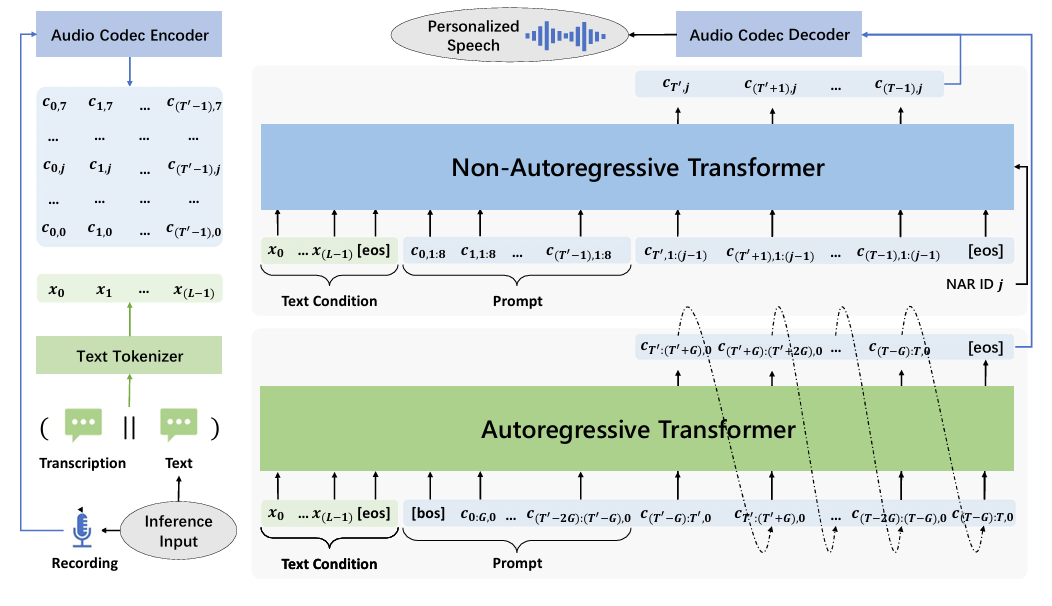
• Autoregressive Model Inference
  • 논문은 먼저 AR model을 사용하여 text sequence $\mathbf{x}$와 code prompt $\mathbf{c}_{<T',0}$에 condition 된 target code $\mathbf{c}_{\geq T',0}$의 first code sequence를 생성함
  • 이때 Grouped Code Modeling을 활용하여 grouped code sequence를 AR model에 feed 하고 각 group의 target code를 autoregressive manner로 생성함:
    (Eq. 18) $ \mathbf{c}_{\geq T',0}=\arg\max_{\mathbf{c}_{\geq T',0}}p\left(\mathbf{c}_{\geq T',0} |\mathbf{x},\mathbf{c}_{<T',0};\theta_{AR}\right)$
    (Eq. 19) $\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, =\arg\max_{\mathbf{c}_{\geq T',0}} \sum_{t=T'/G}^{T/G-1}\log p\left(\mathbf{c}_{t\cdot G:(t+1)\cdot G,0}|\mathbf{x},\mathbf{c}_{<t\cdot G,0} ;\theta_{AR}\right)$
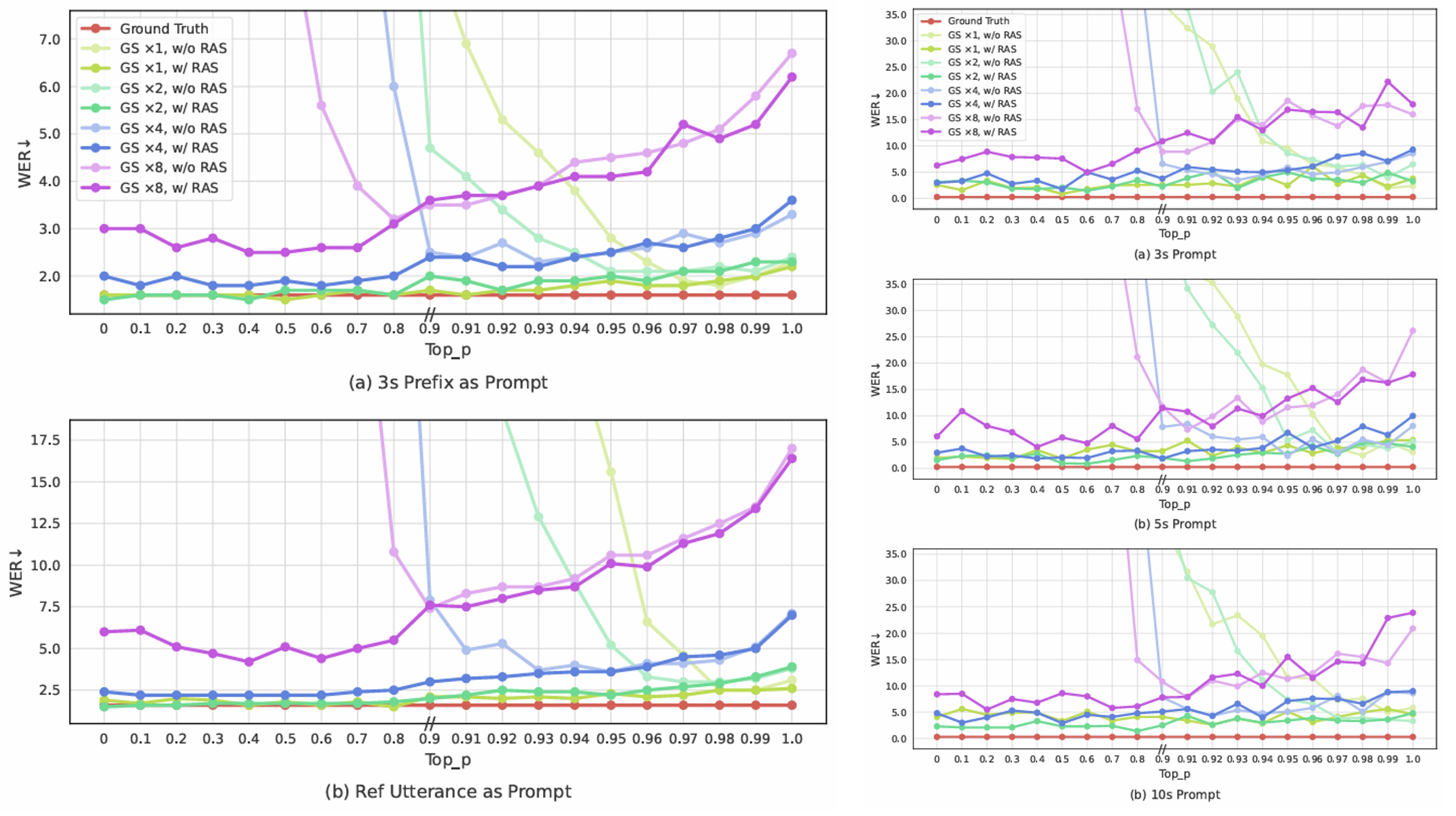
    (Eq. 20) $\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, =\arg\max_{\mathbf{c}\geq T',0}\sum_{t=T'/G}^{T/G-1}\sum_{t'=t\cdot G}^{(t+1)\cdot G-1} \log p\left(c_{t',0}|\mathbf{x},\mathbf{c}_{<t\cdot G,0};\theta_{AR}\right)$
  • VALL-E의 random sampling method와 달리 VALL-E2에서는 decoding stability를 위해 아래 [Algorithm 1]과 같은 Repetition Aware Sampling을 도입함 
    1. 먼저 AR model이 predict 한 probability distribution $p(c_{t'}|\mathbf{x},\mathbf{c}_{<t\cdot G,0};\theta_{AR})$가 주어지면, pre-defined top-$p$ value $v$를 사용하여 nucleus sampling을 통해 target code $c_{t'}$을 생성함
    2. 다음으로 window size $K$를 사용하여 preceding code sequence에서 token $c_{t'}$의 repetition ratio $r$을 calculate 함
    3. 해당 ratio가 pre-defined threshold ratio $t_{n}$을 exceed 하면 $p(c_{t'}|\mathbf{x},\mathbf{c}_{<t\cdot G,0};\theta_{AR})$에서 random sampling을 통해 target code $c_{t'}$을 replace 함
  • 해당 Repetition Aware Sampling을 통해 infinite loop 문제를 해결할 수 있음
    - 특히 repetition aware sampling은 model inference process에 비해 negligible runtime cost를 가지므로 decoding latency는 증가하지 않음
• Non-Autoregressive Model Inference
  • Target code $\mathbf{c}_{\geq T',0}$의 first code sequence가 주어지면, text condition $\mathbf{x}$와 acoustic condition $\mathbf{C}_{<T'}$을 사용하여 NAR model을 추론하고 target code $\mathbf{C}_{\geq T',\geq 1}$의 reamining code sequence를 생성할 수 있음:
    (Eq. 21) $\mathbf{C}_{\geq T',\geq 1}=\arg\max_{\mathbf{C}_{\geq T',\geq 1}} p\left(\mathbf{C}_{\geq T',\geq 1}| \mathbf{x},\mathbf{C}_{<T'}, \mathbf{c}_{\geq T',0};\theta_{NAR}\right)$
    (Eq. 22) $\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,  =\arg\max_{\mathbf{C}_{\geq T',\geq 1}}\sum_{j=1}^{7}\log p\left( \mathbf{c}_{T',j}|\mathbf{x}, \mathbf{C}_{<T'}, \mathbf{C}_{\geq T',<j};\theta_{NAR}\right)$
  • $2\text{-}8$ code sequence를 생성하기 위해, 논문은 NAR model에서 greedy decoding을 사용함
    - 결과적으로 AR model을 통해 얻어진 first codec code와 함께 whole code matrix $\mathbf{C}_{\geq T'}$은 audio codec decoder에서 target speech waveform을 생성하는 데 사용됨

Repetition Aware Sampling

3. Experiments

- Settings

• Dataset : LibriHeavy
• Comparisons : VALL-E

- Results

• VALL-E2는 LibriSpeech, VCTK에서 기존보다 우수한 성능을 달성함

(좌) LibriSpeech (우) VCTK 에서의 성능

• Repetition aware sampling을 사용하면 decoding stability를 향상할 수 있음

(좌) LibriSpeech (우) VCTK 에서의 Decoding Stability

• MOS 측면에서도 VALL-E2는 우수한 결과를 달성함

(상) LibriSpeech (하) VCTK 에서의 MOS

• Ablation Study
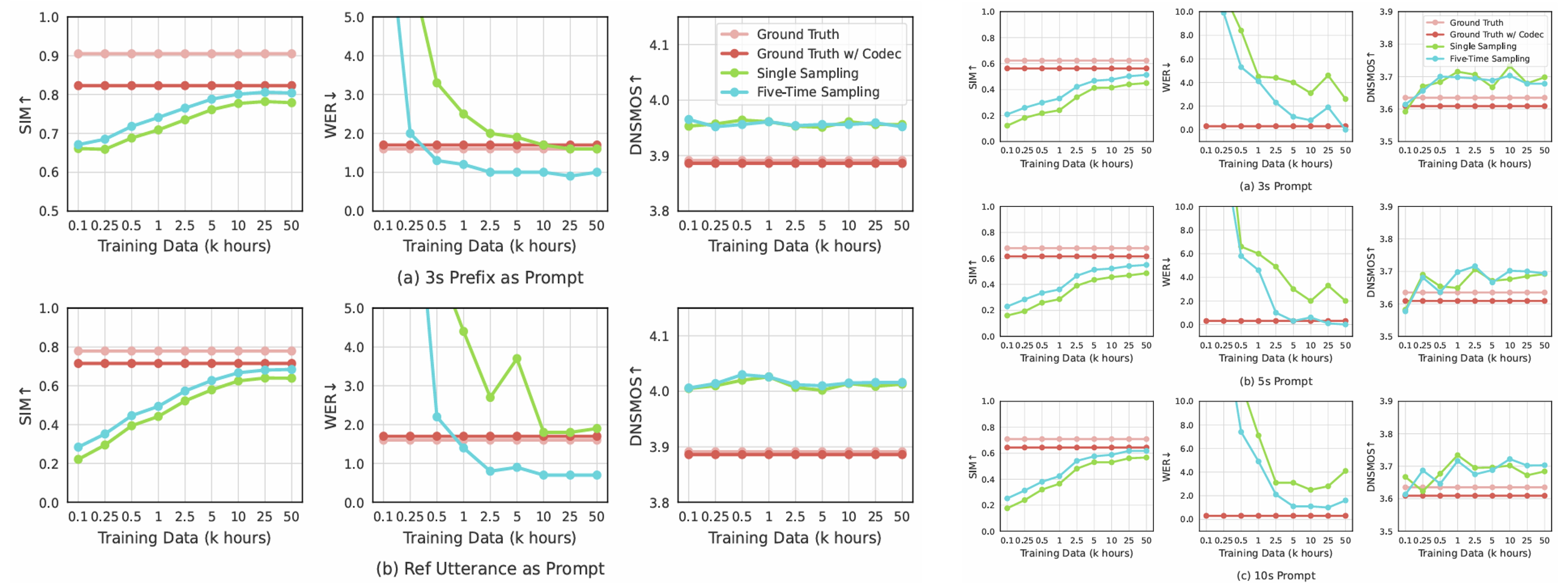
  • Text input, Prompt input 모두 성능 향상에 유효함

(상) LibriSpeech (하) VCTK 에 대한 Ablation Study

• Training data를 scale 하면 더 나은 성능을 달성할 수 있음

(좌) LibriSpeech (우) VCTK 에 대한 Training Data Size 별 성능