[Paper 리뷰] BridgeVoC: Neural Vocoder with Schrodinger Bridge

BridgeVoC: Neural Vocoder with Shrodinger Bridge

---

• Diffusion-based neural vocoder는 mel-spectrogram의 linear-degradation을 neglect 함
• BridgeVoC
  • Time-Frequency domain-based neural vocoder와 Schrodinger Bridge를 연결
  • Mel-spectrogram을 target linear-scale domain으로 project 하고 degraded spectral representation으로 취급
• 논문 (IJCAI 2025) : Paper Link

---

1. Introduction

• Neural vocoder는 acoustic feature로부터 high-quality waveform을 생성할 수 있음
  • 이때 WaveGlow, HiFi-GAN과 같은 Non-Autoregressive (NAR) vocoder는 parallel synthesis를 제공함
  • 최근의 Vocos, APNet과 같은 Time-Frequency (T-F) domain vocoder는 STFT/iSTFT operation을 활용하여 더 빠른 추론 속도와 더 나은 quality를 달성함
  • 한편으로 WaveGrad, DiffWave, PriorGrad와 같은 diffusion-based vocoder는 natural-sounding audio를 얻을 수 있다는 장점이 있음
    1. 특히 diffusion vocoder는 mel-spectrogram에 condition 된 Gaussian noise/prior를 refine 하는 noise-to-data pipeline을 활용함
    2. BUT, noise-to-data process는 추론 속도의 한계가 있음

-> 그래서 T-F domain에서 noise-to-data pipeline을 corrupted/target spectrogram 간의 data-to-data process로 확장한 BrdigeVoC를 제안

 

• BridgeVoC
  • Linear-to-Mel transform으로 derive 된 mel-spectrogram을 Range-Null Decomposition (RND) 기반의 pseudo-inverse를 사용하여 linear-scale domain으로 re-project
    - 이를 통해 target에 대한 strong structural information을 제공하고 이후 mel-spectrogram으로부터 ground-truth mel-spectrogram을 reconstruct 함
  • 특히 Schrodinger Brdige (SB) framework를 활용하여 waveform generation과 restoration을 연결

< Overall of BridgeVoC >

• Schrodinger Bridge를 활용하여 data-to-data pipeline을 구성한 T-F domain-based neural vocoder
• 결과적으로 기존보다 우수한 성능을 달성

2. Motivation

- Signal Models

• T-F domain에서 speech denoising을 위한 signal model을 고려하자
  • 이는 다음과 같이 represent 됨:
    (Eq. 1) $X_{t,f}=S_{t,f}+N_{t,f}$
    - $\{X,S,N\}\in\mathbb{C}^{T\times F}$ : 각각 mixture, target, noise signal, $t,f$ : 각각 time/frequency index
  • Vocoding task를 위한 mel-spectrogram $Y^{mel}\in\mathbb{R}^{T\times F_{mel}}$은 다음 singal model을 통해 얻어짐:
    (Eq. 2) $Y^{mel}=|S|\mathcal{A}$
    - $\mathcal{A}\in\mathbb{R}^{F\times F_{mel}}$ : linear mel-filter로써 compression을 위해 $F_{mel}\ll F$로 설정됨
    - 해당 transformation은 phase를 discard 하고 frequency dimension을 linearly compress 함

- Range-Null Space Decomposition

• Noise-free scenario에서 classical signal compression physical model에서 target $\mathbf{x}\in\mathbb{R}^{D}$와 observed signal $\mathbf{y}\in\mathbb{R}^{d}$는 $\mathbf{y}=\mathbf{Ax}$로 simplify 됨
  • $\mathbf{A}\in\mathbb{R}^{d\times D}$의 pseudo-inverse가 $\mathbf{A}^{\dagger}\in\mathbb{R}^{D\times d}$로 정의된다고 하면 $\mathbf{AA}^{\dagger}\mathbf{A}\equiv \mathbf{A}, d\ll D$를 만족함
  • 그러면 signal $\mathbf{x}$는 2개의 orthogonal sub-space로 decompose 됨:
    (Eq. 3) $\mathbf{x}\equiv \mathbf{A}^{\dagger}\mathbf{Ax}+(\mathbf{I}-\mathbf{A}^{\dagger}\mathbf{A})\mathbf{x}$
    - $\mathbf{A}^{\dagger}\mathbf{Ax}$ : range-space component, $(\mathbf{I}-\mathbf{A}^{\dagger}\mathbf{A})\mathbf{x}$ : null-space component
  • (Eq. 2), (Eq. 3)을 비교해 보면 mel-spectrogram이 range space로 convert 되어 있음
    1. 즉, (Eq. 3)에서 등호의 right-hand side에서 $\mathcal{A}$의 pseudo-inverse $\mathcal{A}^{\dagger}$를 left-multiplying 하여 얻어짐
    2. 이때 null-space component는 unknown이므로 vocoding task는 range-space component가 prior input으로 주어진 target estimation problem으로 formulate 할 수 있음
       - 이는 classical signal recovery problem에 해당함
    3. 그러면 generative approach를 사용하여 remaining null-space component를 effectively recover 할 수 있음
  • 결과적으로 Range-Null Decomposition (RND) theory 측면에서 target signal은 structural sparseness prior에 기반한 linearly-compressed representation으로부터 recover 될 수 있음

- Rank Analysis

• 논문은 RND를 따라 mel-spectrogram을 original linear-scale로 mapping 하기 위해 pseudo-inverse를 사용함 
  • 해당 process는 다음과 같음:
    (Eq. 4) $\hat{Y}=Y^{mel}\mathcal{A}^{\dagger}=|S|\mathcal{AA}^{\dagger}$
    - $\mathcal{A}^{\dagger}\in\mathbb{R}^{F_{m}\times F}$ : pseudo-inverse transform matrix로써 $\mathcal{AA}^{\dagger}\mathcal{A}\equiv \mathcal{A}$를 만족함
    - Linear-scale reprsentation $\hat{Y}\in\mathbb{R}^{T\times F}$는 target signal $S$의 feature dimension과 match 함
  • 여기서 $\hat{Y}$에 zero-phase component를 append 하여 complex form $S^{\dagger}\in\mathbb{C}^{T\times F}$를 얻을 수 있음:
    (Eq. 5) $S^{\dagger}=\hat{Y}+i\cdot \mathbf{0}$
    - $\mathbf{0}\in\mathbb{R}^{T\times F}$ : zero-matrix
  • $S^{\dagger}$를 $S$로 mapping 하는 것은 speech denoising과 유사한 restoration task에 해당하지만, vocoding task는 spectral rank를 reduce 해야 함
    1. Spectral rank change를 나타내기 위해 $\mathcal{R}(\cdot):\mathbb{R}^{T\times F}\rightarrow \mathbb{Z}$를 matrix rank operation으로 정의하면
    2. Basic rank property에 의해 다음을 얻을 수 있음:
       (Eq. 6) $\mathcal{R}(|X|)\approx \mathcal{R}(|S|+|N|)\leq \mathcal{R}(|S|)+\mathcal{R}(|N|)$
       (Eq. 7) $\mathcal{R}(\hat{Y})=\mathcal{R}(|S|\mathcal{AA}^{\dagger})\leq \min\{\mathcal{R}(|S|),\mathcal{R}(\mathcal{AA}^{\dagger})\}$
       - (Eq. 6), (Eq. 7)에서 rank는 signal energy와 closely relate 된 eigenvalue와 연관되어 있으므로 phase component는 omit 함
    3. (Eq. 6)은 mixture spectrum $X$의 rank에 대한 upper bound를 제공함
       - 즉, noise $N$을 add 하면 matrix rank의 upper bound가 증가하고 noise가 strong 할수록 더 높은 upper bound를 가짐
    4. (Eq. 7)은 mel-band 수 $\mathcal{R}(\mathcal{AA}^{\dagger})$가 감소함에 따라 rank $\mathcal{R}(\hat{Y})$도 감소함
  • 결과적으로 noise-induced/mel-oriented degradation 간의 rank distribution disparity는 아래 그림과 같이 나타나고, degraded/target spectrum 간의 rank difference는 다음과 같이 calculate 됨:
    (Eq. 8) $\Delta\mathcal{R}^{denoising}=\mathcal{R}(|X|)-\mathcal{R}(|S|)$
    (Eq. 9) $\Delta\mathcal{R}^{vocoding}=\mathcal{R}(\hat{Y})-\mathcal{R}(|S|)$
  • Noise degradation은 Signal-to-Noise Ratio (SNR)에 따라 mild/moderate/heavy의 3가지 level로 구분됨
    1. Vocoding에서는 서로 다른 spectral compression을 represent 하기 위해 $(40,80,100)$의 mel-band configuration을 사용하고, STFT operation은 257-dimensional feature를 생성함
    2. 이때 noise level이 높을수록 spectral rank도 커지므로 sparsity를 hinder 하고 mel-band compression이 클수록 negative rank difference가 발생함
       - 따라서 matrix rank 측면에서 vocoder는 speech enhancement와 같이 degradation과 target spectra 간의 rank difference를 줄이는 restoration paradigm을 활용할 수 있음

Rank Difference

3. Method

• BridgeVoC는 Schrodinger Brdige (SB)-based T-F domain vocoder에 해당함

- Score-based Generative Models

• Data distribution $p_{data}(x),\,\,x\in\mathbb{R}^{d}$가 주어졌을 때 Score-based Generative Model (SGM)은:
  • Forward Stochastic Differential Equation (SDE)로 정의되는 continuous-time diffusion process로 구축됨:
    (Eq. 10) $ \text{d}x_{t}=f(x_{t},t)\text{d}t+g(t)\text{d}w_{t},\,\,\, x_{0}\sim p_{0}=p_{data}$
    - $t\in[0,T]$ : finite time index, $x_{t}\in\mathbb{R}^{d}$ : process의 state, $f$ : vector-valued drift term, $g$ : scalar-valued diffusion term, $w_{t}\in\mathbb{R}^{d}$ : standard Wiener process
    - 이때 boundary distribution이 Gaussian prior distribution $p_{prior}=\mathcal{N}(0,\sigma^{2}_{T}I)$가 되도록 drift term $f$와 diffusion term $g$를 구성함
  • 그러면 forward SDE에 대한 reverse SDE는 다음과 같이 얻어짐:
    (Eq. 11) $\text{d}x_{t}=\left[f(x_{t},t)-g^{2}(t)\nabla\log p_{t}(x_{t})\right]\text{d}t +g(t)\text{d}\bar{w}_{t},\,\,\, x_{T}\sim p_{T}\approx p_{prior}$
    - $\bar{w}_{t}$ : reverse-time Wiener process, $\nabla \log p_{t}(x_{t})$ : marginal distribution $p_{t}$에 대한 score function
    - $t=0$에서 sampling 된 data를 활용하기 위해, score function을 score network $s_{\theta}(x_{t},t)$로 replace 하고 $t=T$에서 $p_{prior}$로 reversely solve 할 수 있음
  • Score network는 denoising score matching objective를 통해 학습됨:
    (Eq. 12) $\mathbb{E}_{p_{0}(x_{0})p_{t|0}(x_{t}|x_{0}),t}\left[\left|\left| s_{\theta}(x_{t},t)-\nabla\log p_{t|0}(x_{t}|x_{0})\right|\right|_{2}^{2}\right]$
    - 여기서 $t\sim \mathcal{U}(0,T)$이고, $p_{t|0}$는 $x_{0}$에서 $x_{t}$로의 conditional transition distribution으로써 forward SDE를 통해 pre-define 되고 linear drift $f(x_{t},t)=f(t)x_{t}$에 대해서는 analytical 함

Overview

- Schrodinger Bridge

• Schrodinger Bridge (SB)는 constrained boundary를 가지는 path measure를 optimize 하기 위해 사용됨
  • Vocoding task의 경우 target distribution $p_{S}$를 data distribution $p_{data}$, $S^{\dagger}$의 distribution를 prior distribution $p_{S^{\dagger}}$로 취급함
  • Boundary에서 $p$의 marginal distribution $p_{0}, p_{T}$를 고려하면, SB는 Kullback-Leibler (KL) divergence의 minimization으로 정의할 수 있음:
    (Eq. 13) $ \min_{p\in \mathcal{P}_{[0,T]}}D_{KL}(p||p_{ref}),\,\,\, \text{s.t.}\,\,\, p_{0}=p_{S}, p_{T}=p_{S^{\dagger}}$
    - $\mathcal{P}_{[0,T]}$ : reference path measure $p_{ref}$의 finite time index $[0,T]$에 대한 path measure space
  • $p_{ref}$가 (Eq. 10)의 SGM과 동일한 forward SDE로 정의되면 SB problem은 forward-backward SDE와 equivalent 함:
    (Eq. 14) $\text{d}x_{t}=\left[f(x_{t},t)+g^{2}(t)\nabla\log \Psi_{t}(x_{t})\right]\text{d}t+g(t)\text{d}w_{t}, \,\,\, x_{0}\sim p_{S}$
    (Eq. 15) $\text{d}x_{t}=\left[f(x_{t},t)+g^{2}(t)\nabla\log \hat{\Psi}_{t}(x_{t})\right]\text{d}t+g(t)\text{d}\bar{w}_{t}, \,\,\, x_{T}\sim p_{S^{\dagger}}$
    - $f,g,w_{t}$ : (Eq. 10)과 같음
    
  • $\Psi_{t},\hat{\Psi}_{t}$의 optimal forward/reverse drift를 사용하여 SB state $x_{t}$의 marginal distribution은 $p_{t}=\hat{\Psi}_{t}\Psi_{t}$와 같이 express 할 수 있음
    - SB는 fully-tractable 하지 않고 closed-form solution은 $p_{ref}$가 strictly limit 되는 경우에만 존재함

- Schrodinger Bridge Between Paired Data

• Maximum time $T=1$이라고 가정하자
  • Linear drift가 있는 SDE에서 Gaussian-smoothed paired data 간의 tractable SB를 위해 $p_{S}=\mathcal{N}_{\mathbb{C}}(x_{0},\epsilon_{0}^{2}I)$와 $p_{S^{\dagger}}=\mathcal{N}_{\mathbb{C}}(x_{1},e^{2\int_{0}^{1}f(\tau)\text{d}\tau}\epsilon_{0}^{2}I)$의 Gaussian boundary condition을 고려함
  • $\epsilon_{0}\rightarrow 0$일 때 $\hat{\Psi}_{t}, \Psi_{t}$는 target data $x_{0}$와 corrputed data $x_{1}$ 간의 tractable solution으로 수렴함:
    (Eq. 16) $\hat{\Psi}_{t}=\mathcal{N}_{\mathbb{C}}(\alpha_{t}x_{0},\alpha_{t}^{2}\sigma_{t}^{2}I), \,\,\, \Psi_{t}=\mathcal{N}_{\mathbb{C}}(\bar{\alpha}_{t}x_{1},\alpha_{t}^{2}\bar{\sigma}_{t}^{2}I)$
    - $\alpha_{t}=e^{\int_{0}^{t}f(\tau)\text{d}\tau},\bar{\alpha}_{t}=e^{-\int_{t}^{1}f(\tau)\text{d}\tau}$
    - $\sigma^{2}_{t}=\int_{0}^{t}\frac{g^{2}(\tau)}{\alpha_{\tau}^{2}}\text{d}\tau, \bar{\sigma}^{2}_{t}=\int_{t}^{1}\frac{g^{2}(\tau)}{\alpha_{\tau}^{2}}\text{d}\tau$
  • 이는 reference SDE의 $f,g$에 의해 결정되고 SGM의 noise schedule과 analogous 함:
    (Eq. 17) $p_{t}=\Psi_{t}\hat{\Psi}_{t}=\mathcal{N}\left(\frac{\alpha_{t}\bar{\sigma}_{t}^{2}x_{0}+\bar{\alpha}_{t} \sigma^{2}_{t}x_{1}}{\sigma_{1}^{2}},\frac{\alpha_{t}^{2} \bar{\sigma}_{t}^{2}\sigma^{2}_{t}}{\sigma^{2}_{1}}I\right)$
  • Variance Preserving (VP), Variance Exploding (VE), $\text{gmax}$에 대한 noise schedule은 아래 표와 같음
    - $\Delta\beta=\beta_{1}-\beta_{0}$

Noise Schedule

- Loss Function

• 논문은 neural network $B_{\theta}$가 reconstruction, adversarial loss를 training criteria로 사용하여 target data를 directly predict 하도록 함
  • $S$를 target signal, $\tilde{S}=B_{\theta}(x_{t},x_{T},t)$가 neural network의 current estimation이라고 하자
  • Pseudo-inverse를 사용하여 mel-spectrogram을 original uncompressed linear-scale spectrogram으로 re-mapping 한다고 가정하면
    1. Mel-domain에서 amplitude information을 추출하는 경우 original linear-scalin information을 better reconstruct 할 수 있음
    2. 따라서 reconstruction loss는 Mean Squared Error (MSE) loss $\mathcal{L}_{mse}, mel-loss $\mathcal{L}_{mel}$로 구성됨
    3. 이때 MSE loss는 STFT domain에서 $\tilde{S}, S$ 간의 MSE로 정의됨:
       (Eq. 18) $\mathcal{L}_{mse}=\frac{1}{FT}\sum_{f,t}\left|\left| \tilde{S}_{f,t}-S_{f,t}\right|\right|^{2}_{2}$
       - Mel-loss는 APNet을 따름
  • Adversarial loss는 discriminator $D_{m}$과 generator $B_{\theta}$에 대한 hinge GAN loss로 정의됨:
    (Eq. 19) $\mathcal{L}_{d}=\frac{1}{M}\sum_{m=1}^{M}\max(0,1-D_{m}(s))+\max(0,1+D_{m}(\tilde{s}))$
    (Eq. 20) $\mathcal{L}_{g}=\frac{1}{M}\sum_{m=1}^{M}\max(0,1-D_{m}(\tilde{s}))$
    - $\tilde{s}\in \text{iSTFT}(\tilde{S})\in\mathbb{R}^{L}$ : reconstructed waveform
    - $\text{iSTFT}(\cdot)$ : iSTFT operation, $M$ : sub-discriminator 수
    - Discriminator는 HiFi-GAN의 Multi-Period Discriminator, UnivNet의 Multi-resolution Spectrogram Discriminator로 구성됨
  • 추가적으로 feature matching loss는:
    (Eq. 21) $\mathcal{L}_{fm}=\frac{1}{LM}\sum_{l,m}\left|f_{l}^{m}(\tilde{s})-f_{l}^{m}(s)\right|$
    - $f_{l}^{m}(\cdot)$ : $m$-th sub-discriminator의 $l$-th layer feature
  • 결과적으로 얻어지는 final loss는:
    (Eq. 22) $\mathcal{L}_{B}=\mathcal{L}_{mse}+\lambda_{mel}\mathcal{L}_{mel}+\lambda_{g}\mathcal{L}_{g}+\lambda_{fm}\mathcal{L}_{fm}$ 
    - $\lambda_{mel},\lambda_{g},\lambda_{fm}$ : weight hyperparameter

4. Experiments

- Settings

• Dataset : LJSpeech, LibriTTS
• Comparisons : WaveGlow, HiFi-GAN, BigVGAN, iSTFTNet, UnivNet, Avocodo, APNet, Vocos, FreeV, DiffWave, FreGrad, PriorGrad

- Results

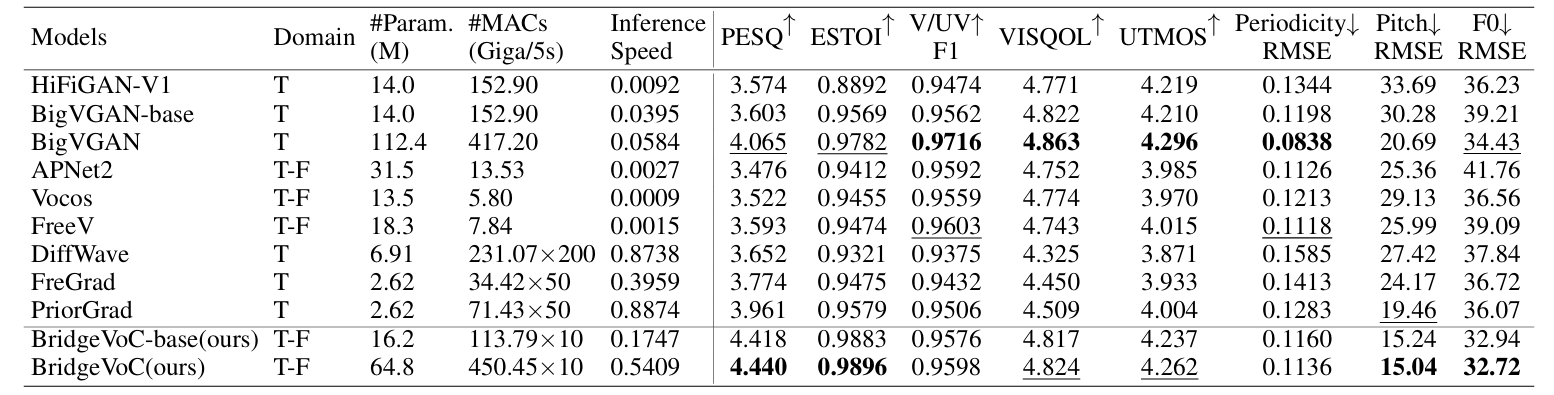
• 전체적으로 BridgeVoC의 성능이 가장 뛰어남

LJSpeech에서의 결과

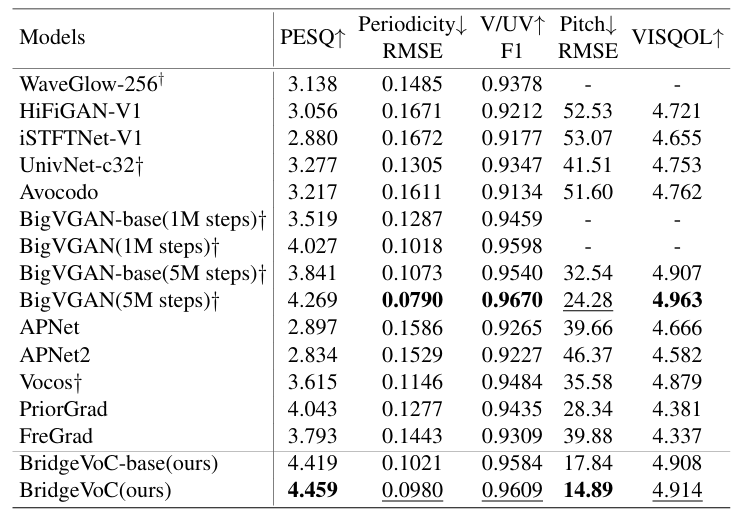
• LibriTTS dataset에 대해서도 BridgeVoC가 가장 우수한 성능을 보임

LibriTTS에서의 결과

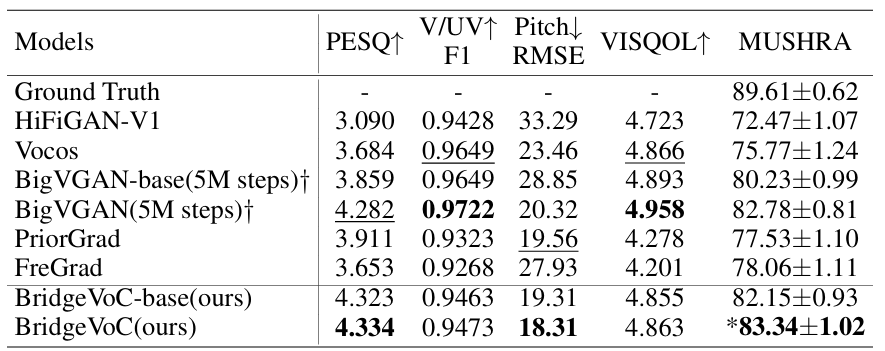
• Out-of-Domain dataset인 VCTK에 대해서도 뛰어난 성능을 보임

VCTK에서의 결과

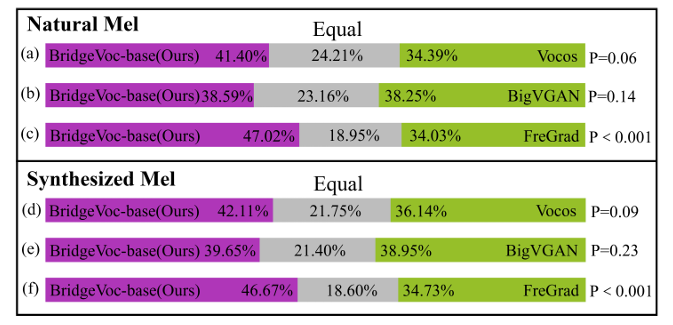
• ABX test 측면에서도 BridgeVoC가 가장 선호됨

ABX Test

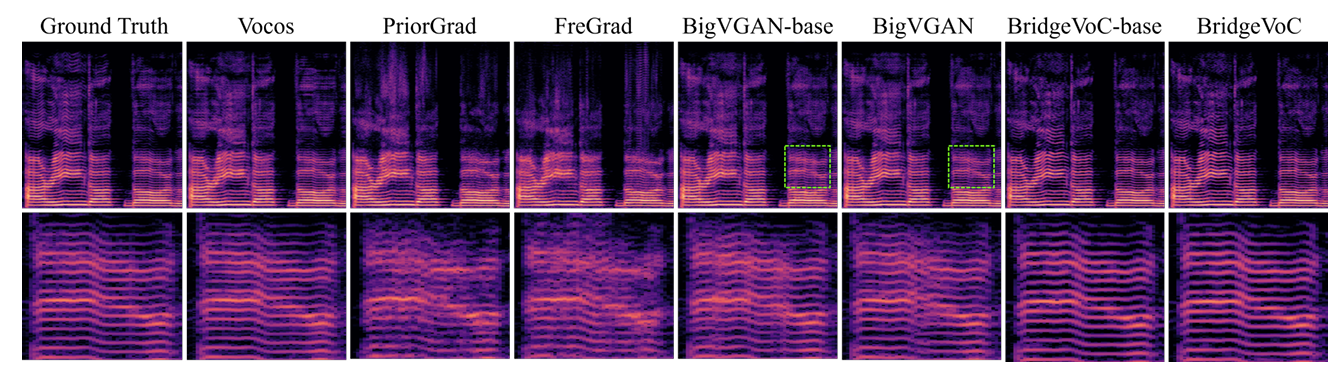
• Spectrogram 측면에서도 BridgeVoC는 harmonic detail을 효과적으로 recover 함

Spectrogram 비교

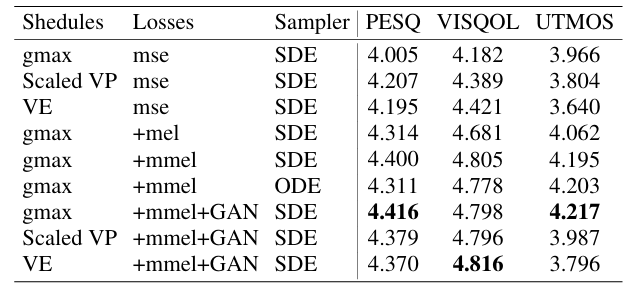
• Ablation Study
  • mmel, GAN loss를 사용하는 경우 최적의 성능을 달성함

Loss Function

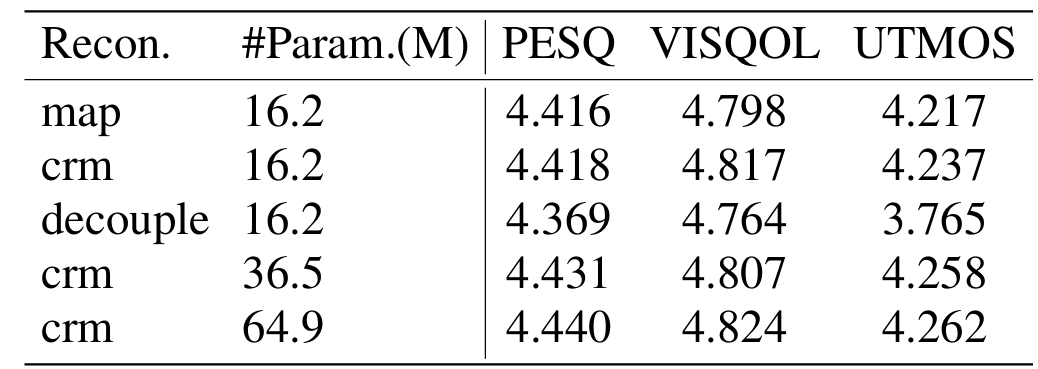
• Signal reconstruction 시 complex masking을 사용하면 더 나은 성능을 달성할 수 있음

Signal Reconstruction

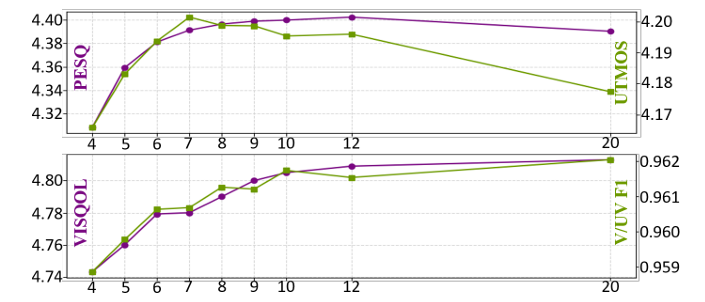
• 7~10의 sampling step을 사용하면 최적의 결과를 얻을 수 있음

Sampling Step