[Paper 리뷰] Quad-Net: Melspectrogram Vocoder with Convolutional Layers Restricted by the Quadrature Mirror Filter for Perfect Reconstruction

Quad-Net: Melspectrogram Vocoder with Convolutional Layers Restricted by the Quadrature Mirror Filter for Perfect Reconstruction

---

• 기존의 neural vocoder는 fixed signal processing filter에 의존하므로 hyperparameter flexibility가 부족함
• Quad-Net
  • Quadrature mirror synthesis filter bank로 shape 된 restricted convolutional layer를 활용
  • Perfect reconstruction filter bank에서 derive 된 perfect reconstruction loss를 통해 model을 optimize 하여 filter length와 data-drivenness를 효과적으로 control
• 논문 (ICASSP 2025) : Paper Link

---

1. Introduction

• Text-to-Speech (TTS), Voice Conversion (VC) 등의 task는 일반적으로 two-stage로 구성됨
  • First stage에서는 practical acoustic feature를 생성하고 second stage에서는 vocoder를 통해 해당 acoustic feature를 raw audio로 변환함
    - 이때 MelGAN, HiFi-GAN과 같은 neural network vocoder를 활용할 수 있음
  • 한편으로 signal processing에서 filter는 signal을 decompose하고 reconstruct 하는데 활용됨
    1. Perfect reconstruction filter bank의 경우 original signal을 separate frequency band에서 parallel downsampled signal로 decompose 한 다음 reconstruction을 수행함
       - 해당 filter를 neural network와 integrate하면 iSTFTNet, Multi-Band MelGAN, Basis-MelGAN 등과 같이 inference speed와 합성 품질을 모두 향상할 수 있음
    2. BUT, 기존 방식은 mathematically restricted parameterized filter가 아닌 data-driven method나 fixed filter에만 의존함

-> 그래서 restricted parameterized filter에 기반한 neural vocoder인 Quad-Net을 제안

 

• Quad-Net
  • Upsampling Multi-Receptive Field Fusion (UMRF) module과 4-channel Perfect Reconstruction Synthesis (4RPS) block을 integrate
    - 구조적으로 4RPS block은 convolution, trimming을 지원하는 2-channel PRS block으로 구성됨
  • Restricted trainable parameter를 가지는 2PRS filter를 통해 다양한 length에 대한 data-driven approach를 제공 

< Overall of Quad-Net >

• 4RPS block을 활용한 restricted parameterized neuarl vocoder
• 결과적으로 기존보다 우수한 성능을 달성

2. Background

- Perfect Reconstruction Filter Banks

• Perfect reconstruction은 signal을 transforming 이후에 original form으로 completely restore 하는 것을 의미함
  • Synthesis filter를 analysis filter의 inverse $h_{0}(-n), h_{1}(-n)$이라고 하자
    1. 아래 (a)에서 2-channel Perfect Reconstruction Filter Bank (PRFB)의 analysis filter bank는 input signal을 2-channel signal로 decompose 한 다음, downsampling을 수행함
    2. (b)에서 synthesis filter bank는 2-channel signal을 upsampling하고 convolution을 통해 combine 되어 original signal을 reconstruct 함
       
  • 해당 과정은 output signal이 distortion 없이 input signal과 closely match 하는 perfect reconstruction을 달성하는 것을 목표로 함
    1. 이때 $z$-transform은:
       (Eq. 1) $ Y(z)=\frac{1}{2}H_{0}(1/z)\left[ H_{0}(z)X(z)+H_{0}(-z)X(-z)\right]+\frac{1}{2}H_{1}(1/z)\left[H_{1}(z)X(z)+H_{1}(-z)X(-z)\right]$
    2. 한편으로 perfect reconstruction을 위해서는 $x,y$가 같아야 하므로 이때 condition은:
       (Eq. 2) $\frac{1}{2}H_{0}(1/z)H_{0}(z)+\frac{1}{2}H_{1}(1/z)H_{1}(z)=1$
       (Eq. 3) $H_{0}(1/z)H_{0}(-z)+H_{1}(1/z)H_{1}(-z)=0$
    3. 그러면 두 filter 간의 quadrature mirror equation은:
       (Eq. 4) $H_{1}(z)=z^{-L}H_{0}(-1/z),\,\,\,\text{with}\,\,L\,\,\text{odd}$
       - $L$ : filter length
    4. (Eq. 4)에 따라 (Eq. 3)은 항상 만족하므로, autocorrelation $r_{0}(n):=h_{0}(n)*h_{0}(-n)$에 대해 (Eq. 2)는:
       (Eq. 5) $R_{0}(z)+R_{0}(-z)=2\Leftrightarrow r_{0}(2n)=\delta(n)$
  • 구조적으로 논문은 neural network를 위해 2-channel PRFB를 elementary cell로 사용하는 4-channel PRFB를 채택함

Perfect Reconstruction (a) Analysis Filter Bank (b) Reconstruction Filter Bank

3. Method

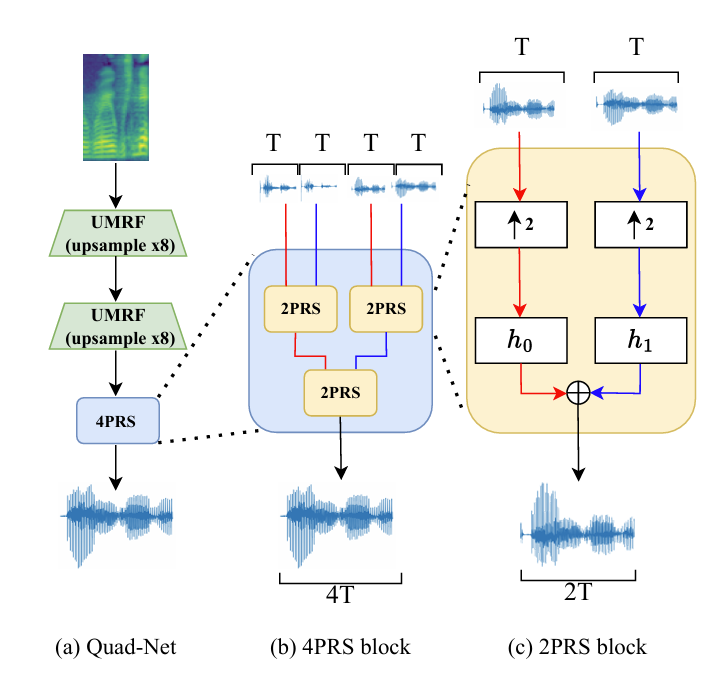
• Quad-Net은 2개의 UMRF block과 3개의 2-channel Perfect Reconstruction Synthesis (2PRS) block을 기반으로 4-channel Perfect Reconstruction Synthesis (4PRS) block을 구성함
  • 여기서 UMRF module은 HiFi-GAN을 따라 mel-spectrogram input을 high-fidelity audio output으로 convert 하는 fully-convolutional network에 해당함
  • 해당 UMRF block을 통해 생성된 4개의 signal은 4PRS block으로 전달됨

Quad-Net

- 4-Channel Perfect Reconstruction Synthesize Block

• 논문은 아래 그림의 (a)와 같은 elementary cell을 활용하여 4PRS block을 구성함
  • (b)에서 signal $x$는 2개의 signal로 decompose 되고 4개의 signal $z_{1},..., z_{4}$로 decompose 된 후 reconstruct 됨
    - 특히 (b)의 elementary cell이 perfect reconstruction condition을 만족하는 경우 $x$는 $y$와 동일함
  • 4PRS block에서 UMRF module의 4-channel $T$-signal은 2개의 2PRS block을 통해 pair로 전달되어 2-channel $2T$-signal을 생성함
    - 최종적으로 해당 signal은 2PRS block을 추가로 통과하여 original signal인 1-channel $4T$-signal을 reconstruct 함
  • 한편으로 2PRS block의 sequence는 두 input signal을 zero-padding을 통해 upsampling 한 다음, quadrature mirror equation에 대한 2개의 filter를 통해 convolution 하고 result를 summation 하는 것을 포함함
    1. 이때 resulting signal length는 input signal의 2배보다 slightly longer 함
       - Convolution으로 인한 boundary problem 때문
    2. 따라서 논문은 2PRS block의 resulting signal이 input signal length의 2배와 match되도록 trimming을 양 side에 적용함
  • 2PRS block은 2-channel PRFB에 대해 다음 3가지 condition을 가짐:
    1. Quadrature Mirror Equation
       - 2PRS block은 (Eq. 4)를 만족해야 함 (즉, $h_{1}(n)=(-1)^{L-n}h_{0}(L-n)$)
    2. Filter Normalization
       - (Eq. 5)에서 $n=0$일 때 derive 되는 condition으로써, 이때 2PRS의 $h_{0}$ filter는:
       (Eq. 6) $r_{0}(0)=\delta(0)\Leftrightarrow h_{0}(n)=\frac{h(n)}{\sqrt{\sum_{i=0}^{L}h(i)^{2}}}$
       - $h(n)$ : $h_{0}, h_{1}$을 control 하는 parameter
       
    3. (Eq. 5)에서 $n$이 $0$이 아닐 때 derive 되는 condition:
       (Eq. 7) $r_{0}(2n)=\delta(n),\,\,(n\neq 0)\Leftrightarrow \sum_{i=1}^{(L-1)/2}r_{0}(2i)^{2}=0$
  • 결과적으로 training은 perfect reconstruction loss $\mathcal{L}_{PR}$을 minimize 하여 얻어짐:
    (Eq. 8) $\mathcal{L}_{PR}=\sum_{j=1}^{(L-1)/2}\left(\sum_{i=0}^{L}h_{0}(i)\times h_{0}(i+2j)\right)^{2}$

(a) 2-Channel PRFB (b) 4-Channel PRFB

- Loss

• 논문은 adversarial loss $\mathcal{L}_{adv}$와 feature matching loss $\mathcal{L}_{FM}$을 활용함
  • 이때 기존 mel-loss를 Multi-Band MelGAN의 multi-resolution STFT loss로 대체함
    1. 해당 loss는 STFT feature의 analysis parameter에 대한 $M$ distinct set을 활용하여 calculate 됨
    2. 추가적으로 논문은 각 $M$ feature에 대해 spectral convergence loss $\mathcal{L}_{sc}$와 log STFT magnitude loss $\mathcal{L}_{mag}$를 calculate 함
    3. Multi-resolution STFT loss $\mathcal{L}_{STFT}$는 모든 $M$ set의 STFT feature에 대해 $\mathcal{L}_{sc},\mathcal{L}_{mag}$를 summation 하여 얻어짐
  • 그러면 final total generator loss $\mathcal{L}_{total}$은:
    (Eq. 9) $\mathcal{L}_{total}=\mathcal{L}_{adv}+\lambda_{FM}\mathcal{L}_{FM}+\lambda_{STFT}\mathcal{L}_{STFT}+\lambda_{PR}\mathcal{L}_{PR}$
    - $\lambda_{FM}=2, \lambda_{STFT}=45$
    - STFT loss analysis parameter의 경우, $(\text{FFT size}, \text{hop size}, \text{window size})$를 각각 $(1024,2048,512), (128, 256, 64), (1024, 2048,512)$로 설정

4. Experiments

- Settings

• Dataset : LJSpeech
• Comparisons : HiFi-GAN, iSTFTNet

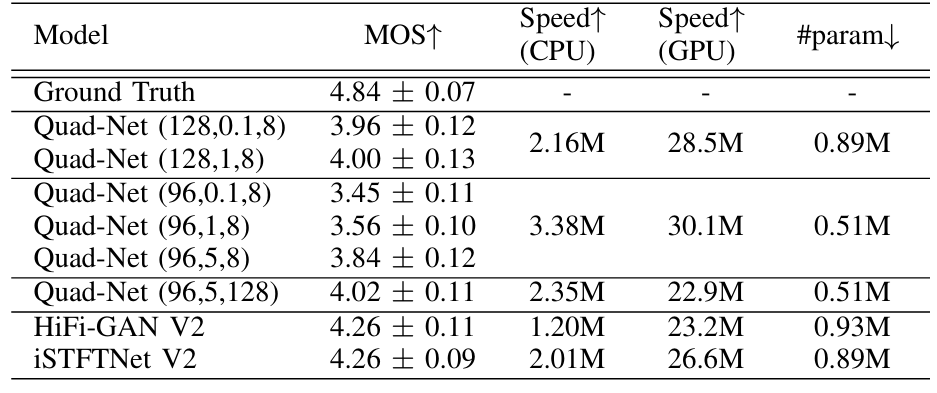
- Results

• Quad-Net은 기존보다 빠른 inference speed와 안정적인 MOS를 달성할 수 있음

전체적인 성능 비교

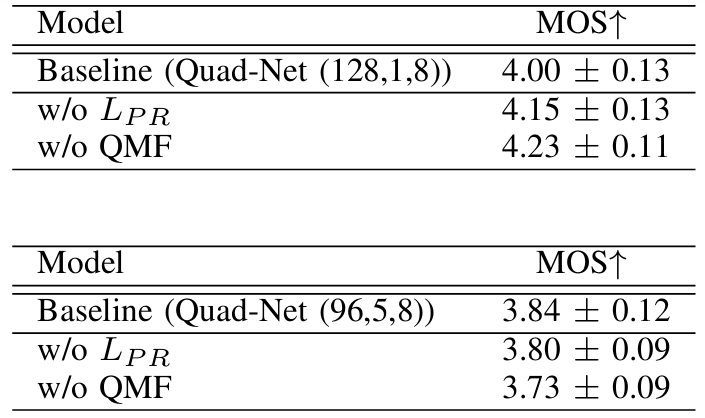
• Ablation Study
  • 각 component를 제거하는 경우 성능 저하가 발생함

Ablation Study

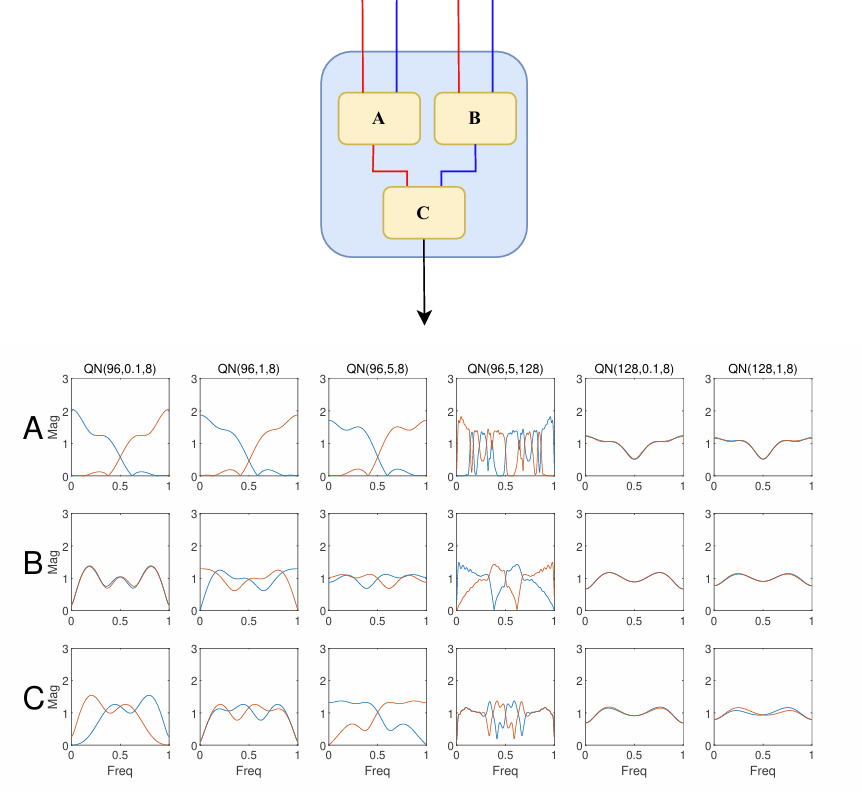
• Filter Analysis
  • 4PRS block에 대한 frequency response를 비교해 보면
  • Quad-Net(96, $\lambda_{PR},8)$에서는 $\lambda_{PR}$이 증가함에 따라 2PRS block의 filter는 bandpass filter와 resemble 함
  • Quad-Net(96,5,128)에서는 complex shape가 나타남

Filter Analysis

• Perfect Reconstruction
  • $\lambda_{PR}=5$인 경우 original speech 수준의 reconstruction이 가능함

Perfect Reconstruction