티스토리 뷰
Paper/Vocoder
[Paper 리뷰] Cauchy Diffusion: A Heavy-Tailed Denoising Diffusion Probabilistic Model for Speech Synthesis
feVeRin 2025. 4. 20. 10:59반응형
Cauchy Diffusion: A Heavy-Tailed Denoising Diffusion Probabilistic Model for Speech Synthesis
- 기존의 denoising diffusion probabilistic model-based vocoder는 prosody diversity를 반영하기 어려움
- Cauchy Diffusion
- Heavy-tailed Cauchy distribution을 통해 imbalanced speech data에 대한 better resilience를 달성
- 결과적으로 diffusion vocoder의 prosody modeling을 향상
- 논문 (AAAI 2025) : Paper Link
1. Introduction
- 최근 Denoising Diffusion Probabilistic Model (DDPM)은 neural vocoder에서 우수한 성능을 보이고 있음
- BUT, DDPM은 imbalanced data를 처리할 때 mode-collapse 문제에 susceptible 함
- 특히 spoken sentence는 다양한 prosody로 인해 상당히 imbalance 하므로 DDPM-based vocoder는 prosody diversity를 효과적으로 반영하지 못함 - 한편으로 Cauchy distribution은 Gaussian distribution과 달리 heavier tail을 가지므로 imbalanced data에 적합함
- 실제로 generative model에 heavy-tailed distribution을 적용하면 synthesized sample의 diversity를 향상할 수 있음
- BUT, DDPM은 imbalanced data를 처리할 때 mode-collapse 문제에 susceptible 함
-> 그래서 Cauchy distribution을 활용하여 DDPM-based vocoder의 prosody modeling을 개선한 Cauchy Diffusion을 제안
- Cauchy Diffusion
- Cauchy distribution을 활용하여 DDPM을 개선하기 위해 Cauchy noise를 사용한 diffusion, generative process를 도입
- 이때 prosody diversity를 향상하기 위해 각 diffusion step에서 noise와 scale이 stochastic sampling을 지원하도록 함 - Ratio distribution을 기반으로 Cauchy distribution을 2개의 Gaussian distribution으로 reprsent 한 다음, same location-scale parameterization 하에서 unify 하여 사용
- 이를 통해 diffusion, generative process에서 Cauchy noise scale은 ratio distribution을 통해 결정될 수 있음 - 추가적으로 Denoising Diffusion Implicit Model (DDIM)의 sampling method를 사용하여 deterministic, stochastic sampling process를 지원
- Cauchy distribution을 활용하여 DDPM을 개선하기 위해 Cauchy noise를 사용한 diffusion, generative process를 도입
< Overall of Cauchy Diffusion >
- Heavy-tailed Cauchy distribution에 기반한 diffusion-based vocoder
- 결과적으로 기존보다 뛰어난 합성 성능을 달성
2. Method
- Cauchy Diffusion은 heavy-tailed Cauchy noise를 활용한 DDPM으로 구성됨
- Background
- 먼저 diffusion model은 unknown data distribution $q(\mathbf{x}_{0})$에서 추출한 sample로부터 $\theta$로 parameterize 된 distribution $p_{\theta}(\mathbf{x}_{0})$을 학습하는 것을 목표로 함
- 여기서 DDPM은 latent variable model로써 다음과 같이 정의됨:
(Eq. 1) $p_{\theta}(\mathbf{x}_{0}):=\int p_{\theta}(\mathbf{x}_{0:T})d\mathbf{x}_{1:T}$
- $\mathbf{x}_{1},...,\mathbf{x}_{T}$ : latent variable - 특히 DDPM은 diffusion process와 reverse process로 구성됨
- Diffusion process는 pre-defined schedule $\beta=\{\beta_{1},...,\beta_{T}\}$에 따라 data에 noise를 gradually add 하는 Markov Chain으로써 다음과 같이 정의됨:
(Eq. 2) $q(\mathbf{x}_{1:T}|\mathbf{x}_{0}):=\prod_{t=1}^{T}q(\mathbf{x}_{t}|\mathbf{x}_{t-1})$ - Reverse process는 pre-defined schedule $\beta$에서 derive 된 schedule로 added noise를 gradually remove 함:
(Eq. 3) $p_{\theta}(\mathbf{x}_{0:T}):=p(\mathbf{x}_{T})\prod_{t=1}^{T}p_{\theta}(\mathbf{x}_{t-1}|\mathbf{x}_{t})$
- Diffusion process는 pre-defined schedule $\beta=\{\beta_{1},...,\beta_{T}\}$에 따라 data에 noise를 gradually add 하는 Markov Chain으로써 다음과 같이 정의됨:
- 여기서 DDPM은 latent variable model로써 다음과 같이 정의됨:
- Cauchy Diffusion Process
- Cauchy distribution은 probability distribution class $\Omega$로 정의되는 location-scale family에 해당함
- 이때 any cumulative distribution function $F\in\Omega$, any real number $a\in\mathbb{R}$, $b>0$에 대해 distribution function $G(x)=F(a+bx)$도 $\Omega$에 속함
- Location-scale distribution은 location과 non-negative scale로 parameterize 되므로, Cauchy diffusion process는:
- 먼저 $\beta_{t},\epsilon_{t}$를 각각 squared scale (pre-defined schedule)과 diffusion step $t$에서 samping 된 standard Cauchy noise라고 하자
- Cauchy distribution은 linear transformation에 대해 close 되어 있으므로 Cauchy distribution의 conditional distribution $q(\mathbf{x}_{t}|\mathbf{x}_{t-1})$은:
(Eq. 4) $\mathbf{x}_{t}=\sqrt{1-\beta_{t}}\mathbf{x}_{t-1}+\sqrt{\beta_{t}}\epsilon_{t}$ - Gaussian DDPM의 reparameterization trick을 Cauchy diffusion process에도 적용할 수 있으므로, $\alpha_{t}:=1=\beta_{t}$, $\bar{\alpha}_{t}:=\prod_{s=1}^{t}\alpha_{s}$라 했을 때 Cauchy diffusion process의 conditional distribution $q(\mathbf{x}_{t}|\mathbf{x}_{0})$는:
(Eq. 5) $\mathbf{x}_{t}=\sqrt{\bar{\alpha}_{t}}\mathbf{x}_{0}+\sqrt{1-\bar{\alpha}_{t}}\epsilon_{t}$
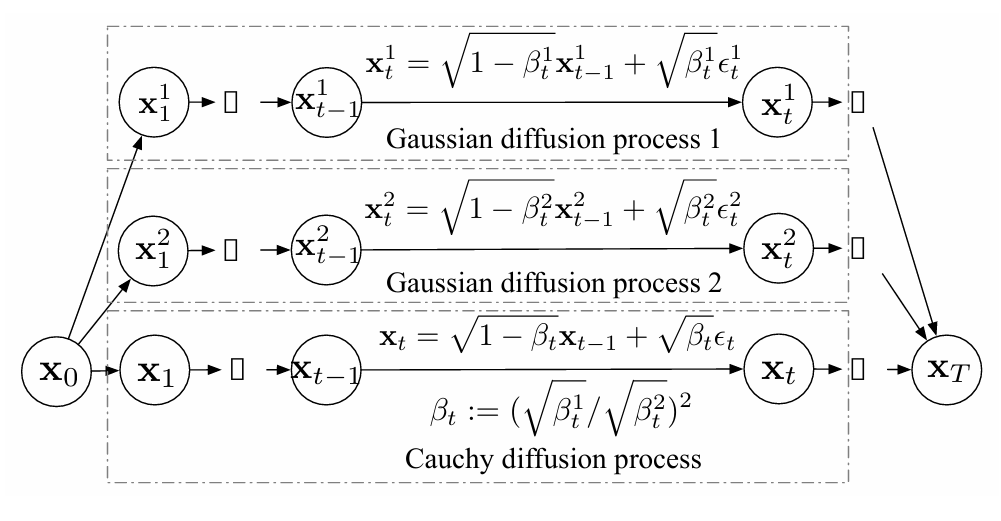
- Cauchy Diffusion Schedule
- Cauchy Diffusion은 generated speech의 prosody diversity를 향상하기 위해 stochastic sampling을 지원하므로, generative process에서 scale prediction이 필요함
- BUT, Cauchy distribution은 Kolmogorv equation을 따르지 않으므로 diffusion process에서 posterior scale을 analytically compute 할 수 없고, generative process에서 scale prediction이 impossible 함
- 결과적으로 linear schedule, consine schedule과 같은 기존의 scheduling을 사용할 수 없으므로 Cauchy Diffusion에 적합한 diffusion schedule이 필요함
- Scale Computation
- Cauchy distribution과 Gaussian distribution은 모두 location-scale family에 속하므로 Gaussian distribution의 variance를 squared scale로 취급하여 parameterization 할 수 있음
- 이때 Cauchy distribution은 zero-mean인 두 normally distributed variable의 ratio이므로, 논문은 Kolmogrov equation을 따르는 두 Gaussian diffusion process의 ratio distribution을 사용하여 Cauchy Diffusion schedule을 구성함
- $\beta^{1}=\{\beta_{1}^{1},...,\beta_{t}^{1},...,\beta_{T}^{1}\}$을 first Gaussian DDPM의 squared scale, $\beta^{2}=\{\beta_{1}^{2},...,\beta_{t}^{2},...,\beta_{T}^{2}\}$을 second Gaussian DDPM의 squared scale이라고 하자
- Diffusion step $t$에서 Cauchy Diffusion의 squared scale은:
(Eq. 6) $\beta_{t}:=\left(\sqrt{\beta_{t}^{1}}/\sqrt{\beta_{t}^{2}}\right)^{2}$
- $\alpha_{t}^{1}:=1-\beta_{t}^{1},\bar{\alpha}_{t}^{1}:=\prod_{i=1}^{t}\alpha_{i}^{1}$을 first Gaussian DDPM, $\alpha_{t}^{2}:=1-\beta_{t}^{2},\bar{\alpha}_{t}^{2}:=\prod_{i=1}^{t}\alpha_{i}^{2}$를 second Gaussian DDPM이라고 하자
- Diffusion step $t$에서 두 Gaussian DDPM의 posterior squared scale은 $\tilde{\beta}_{t}^{1}=(1-\bar{\alpha}_{t-1}^{1})/(1-\bar{\alpha}_{t}^{1})\beta_{t}^{1}$, $\tilde{\beta}_{t}^{2}=(1-\bar{\alpha}_{t-1}^{2})/(1-\bar{\alpha}_{t}^{2})\beta_{t}^{2}$와 같음
- 그러면 diffusion step $t$에서 Cauchy Diffusion의 posterior squared scale은:
(Eq. 7) $\tilde{\beta}_{t}:=\left(\sqrt{\tilde{\beta}_{t}^{1}}/\sqrt{\tilde{\beta}_{t}^{2}}\right)^{2}$
- Reformuation of the Scale Computation
- 두 Gaussian diffusion process의 prior scale을 dividing 하여 Cauchy Diffusion process의 prior scale을 computing 하면 pathological result가 발생함
- 아래 그림의 윗줄과 같이 Cauchy Diffusion process의 prior scale은 unexpectedly high 하므로 거의 모든 지점에서 prior, posterior scale ratio는 0에 approach 함 - 이때 Gaussian diffusion schedule이 아닌 Cauchy Diffusion schedule에 따라 denoising model을 optimize 하므로 prior scale computation을 reformulate 할 수 있음
- 먼저 second Gaussian Diffusion process의 prior scale은:
(Eq. 8) $\sqrt{\beta_{t}^{2}}=\sqrt{\beta_{t}}*\sqrt{\beta_{t}^{1}}$ - Prior scale이 주어지면 second Gaussian distribution process의 posterior scale을 analytically compute 할 수 있고, (Eq. 7)을 사용하여 Cauchy Diffusion process의 posterior scale을 compute 할 수 있음
- 결과적으로 아래 그림의 아랫줄과 같이, 해당 reformulation의 ratio는 healthy 하게 나타남
- 먼저 second Gaussian Diffusion process의 prior scale은:
- 두 Gaussian diffusion process의 prior scale을 dividing 하여 Cauchy Diffusion process의 prior scale을 computing 하면 pathological result가 발생함
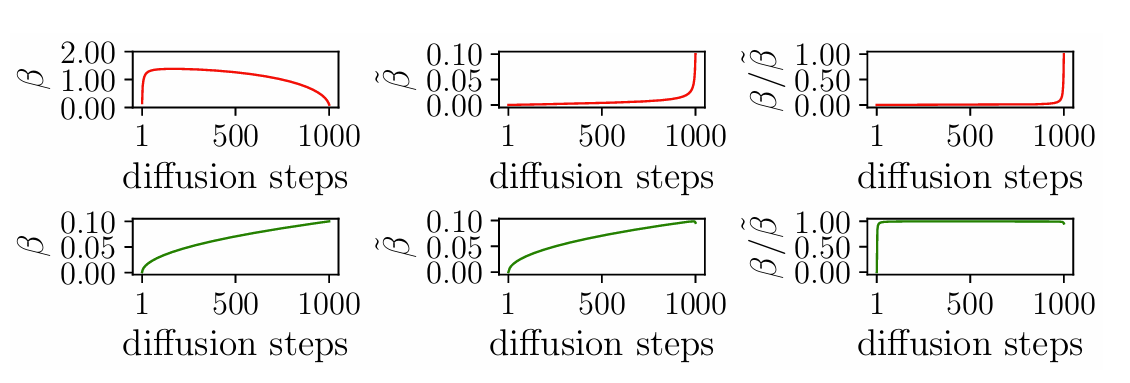
- Training Objective
- Parameter $\theta$는 negative log-likelihood에 대한 variational bound를 optimizing 하여 data distribution $q(\mathbf{x}_{0})$에 대해 fitting 됨
- 여기서 negative log-likelihood의 variational bound는 다음과 같이 formulate 됨:
(Eq. 9) $\mathbb{E}[-\log p_{\theta}(\mathbf{x}_{0})]\leq \mathbb{E}_{q}\left[-\log \frac{p_{\theta}(\mathbf{x}_{0:T})}{q(\mathbf{x}_{1:T}|\mathbf{x}_{0})}\right]$ - Variational bound는 $L:=L_{0}+L_{1}+...+L_{T}$로 decompose 될 수 있음
- $L_{0}:=-\log p_{\theta}(\mathbf{x}_{0}|\mathbf{x}_{1}),L_{t-1}:=D_{KL}\left(q(\mathbf{x}_{t-1}|\mathbf{x}_{t},\mathbf{x}_{0})|| p_{\theta}(\mathbf{x}_{t-1}|\mathbf{x}_{t}) \right),L_{T}:= D_{KL}\left(q(\mathbf{x}_{T}|\mathbf{x}_{0})||p(\mathbf{x}_{T}) \right)$
- $L_{0}$의 evaluation은 task에 따라 달라지고 $L_{T}$는 $\theta$와 independent 하므로 loss term은 parameter $\theta$를 tuning 하는데 중요한 역할을 함 - 한편으로 DDPM에 대해 input $\mathbf{x}_{0}$, added noise $\epsilon_{t}$, diffusion step $t$의 corrupted input $\mathbf{x}_{t}$와 같은 prediction task를 고려할 수 있음
- Cauchy Diffusion은 Gaussian DDPM과 동일한 diffusion process를 share 하므로 added Cauchy noise $\epsilon_{t}$를 predict 하고, (Eq. 10)을 사용하여 주어진 $\mathbf{x}_{t}$에 대한 input $\mathbf{x}_{0}$를 calculate 함:
(Eq. 10) $\mathbf{x}_{0}=\frac{1}{\alpha_{t}}\left(\mathbf{x}_{t}-\frac{\beta_{t}}{\sqrt{1-\bar{\alpha}_{t}}}\epsilon_{t}\right)$ - Added Cauchy noise를 predict 하는 objective는:
(Eq. 11) $\mathcal{L}_{\gamma}(\epsilon_{\theta}):=\sum_{t=1}^{T}\gamma_{t}\mathbb{E}_{\mathbf{x}_{0},t}\left[ \left|\left| \epsilon_{\theta}\left(\sqrt{\bar{\alpha}_{t}}\mathbf{x}_{0}+\sqrt{1-\bar{\alpha}_{t}}\epsilon_{t},t \right)-\epsilon_{t}\right|\right|_{2}^{2}\right]$
- $\epsilon_{t}$ : sampled Cauchy noise, $ \epsilon_{\theta}\left(\sqrt{\bar{\alpha}_{t}}\mathbf{x}_{0}+ \sqrt{1-\bar{\alpha}_{t}}\epsilon_{t},t\right)$ : diffusion step $t$에서 predict 된 Cauchy noise - Coefficient $\gamma_{t}=1$로 설정하면 objective function은 다음과 같이 simplifiy 됨:
(Eq. 12) $\mathcal{L}(\epsilon_{\theta}):=\sum_{t=1}^{T}\mathbb{E}_{\mathbf{x}_{0},t}\left[ \left|\left| \epsilon_{\theta}\left(\sqrt{\bar{\alpha}_{t}}\mathbf{x}_{0}+\sqrt{1-\bar{\alpha}_{t}}\epsilon_{t},t \right)-\epsilon_{t}\right|\right|_{2}^{2}\right]$
- Cauchy Diffusion은 Gaussian DDPM과 동일한 diffusion process를 share 하므로 added Cauchy noise $\epsilon_{t}$를 predict 하고, (Eq. 10)을 사용하여 주어진 $\mathbf{x}_{t}$에 대한 input $\mathbf{x}_{0}$를 calculate 함:
- 해당 simplified objective는 scale에 대한 error signal을 제공하지 못하므로 added noise와 squared scale을 simultaneously predict 할 수 있음
- 여기서 두 Gaussian distribution 간의 KL-divergence를 estimate 하려면 Gaussian distribution의 posterior location을 analytically compute 해야 함
- BUT, Cauchy Diffusion은 Kolmogorov equation을 따르지 않으므로 posterior location을 analytically compute 할 수 없음
- 따라서 논문은 stop-gradient operation을 기반으로 location이 0인 두 distribution 간의 KL-divergence를 compute 함
- 이는 Cauchy Diffusion의 posterior squared scale (Eq. 7)을 사용하여 estimate 될 수 있으므로 viable 함
- 결과적으로 두 Cauchy distribution 간의 KL-divergence term $L_{t}$는:
(Eq. 13) $L_{t}:=\log \frac{\left(\tilde{\beta}_{t}+ \beta_{\theta}\left( \sqrt{\bar{\alpha}_{t}}\mathbf{x}_{0} +\sqrt{1-\bar{\alpha}_{t}}\epsilon_{t},t\right)\right)^{2}}{4\tilde{\beta}_{t}\beta_{\theta}\left(\sqrt{\bar{\alpha}_{t}}\mathbf{x}_{0}+ \sqrt{1-\bar{\alpha}_{t}}\epsilon_{t},t\right)}$
- $\beta_{\theta}\left(\sqrt{\bar{\alpha}_{t}}\mathbf{x}_{0}+ \sqrt{1-\bar{\alpha}_{t}}\epsilon_{t},t\right)$ : predicted Cauchy squared scale - 추가적으로 log-domain에서 Cauchy Diffusion model의 squared scale을 interpolate 하면:
(Eq. 14) $\beta_{\theta}\left(\sqrt{\bar{\alpha}_{t}}\mathbf{x}_{0}+ \sqrt{1-\bar{\alpha}_{t}}\epsilon_{t},t\right)=\exp \left(\text{sigmoid}(v)\log \beta_{t-1}+(1-\text{sigmoid}(v))\log \tilde{\beta}_{t-1}\right)$
- $v$ : denoising network output - 그러면 KL-divergence loss는:
(Eq. 15) $\mathcal{L}(\beta_{\theta}):=\sum_{t=1}^{T-1}L_{t}$
- 최종적으로 얻어지는 Cauchy Diffusion의 training objective는:
(Eq. 16) $\mathcal{L}:=\mathcal{L}(\epsilon_{\theta})+\lambda\mathcal{L}(\beta_{\theta})$
- $\lambda$ : predicted Cauchy noise, squared scale 간의 trade-off
- 여기서 negative log-likelihood의 variational bound는 다음과 같이 formulate 됨:
- Sampling Approach of Cauchy Diffusion
- Cauchy Diffusion에 대한 stochastic sampling은 deterministic sampling 보다 더 나은 diversity를 제공함
- BUT, 기존 sampling approach는 Cauchy Diffusion model이 지원하지 않는 posterior location을 timating 해야 하므로 사용할 수 없음
- 대신 Cauchy Diffusion은 DDIM의 deterministic, stochastic sampling을 활용함
- 해당 sampling method는 predicted $\mathbf{x}_{0}$, $\mathbf{x}_{t}$로의 direction pointing, random noise로 구성됨
- 특히 DDPM의 training objective는 distribution $q(\mathbf{x}_{1:T}|\mathbf{x}_{0})$ 대신 marginal $q(\mathbf{x}_{t}|\mathbf{x}_{0})$에 의존하므로 non-Markovian diffusion process를 통해 generalize 됨 - Cauchy Diffusion은 added Cauchy noise와 해당 scale을 predict 하므로 sampling process는 다음과 같이 정의됨:
(Eq. 17) $\mathbf{x}_{t-1}=\sqrt{\bar{\alpha}_{t-1}}\left(\frac{\mathbf{x}_{t}-\sqrt{1-\bar{\alpha}_{t}}\epsilon_{\theta}}{\sqrt{\bar{\alpha}_{t}}}\right)+\sqrt{1-\bar{\alpha}_{t}- \eta\beta_{\theta}}\epsilon_{\theta}+\sqrt{\eta\beta_{\theta}}\epsilon_{t}$
- $\epsilon_{\theta},\beta_{\theta}$ : 각각 predicted Cauchy noise, squared scale
- $\eta$ : scaling factor로써 sampling procedure 동안 predicted squared scale의 usage를 결정함
- $\eta=0$이면 deterministic sampling이 사용되고, $\eta=1$이면 stochastic sampling이 사용됨
- 해당 sampling method는 predicted $\mathbf{x}_{0}$, $\mathbf{x}_{t}$로의 direction pointing, random noise로 구성됨
3. Experiments
- Settings
- Dataset : LJSpeech, VCTK
- Comparisons : WaveGlow, HiFi-GAN, UnivNet, WaveGrad, DiffWave, PriorGrad, FastDiff
- Results
- LJSpeech에 대해 Cauchy Diffusion이 가장 우수한 성능을 달성함
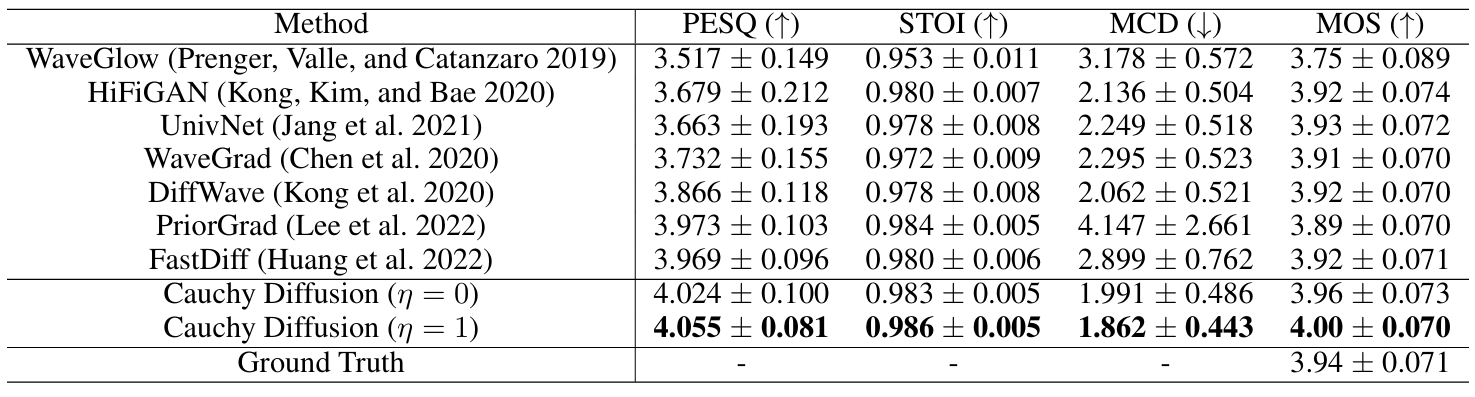
- VCTK도 마찬가지로 Cauchy Diffusion의 성능이 가장 뛰어남
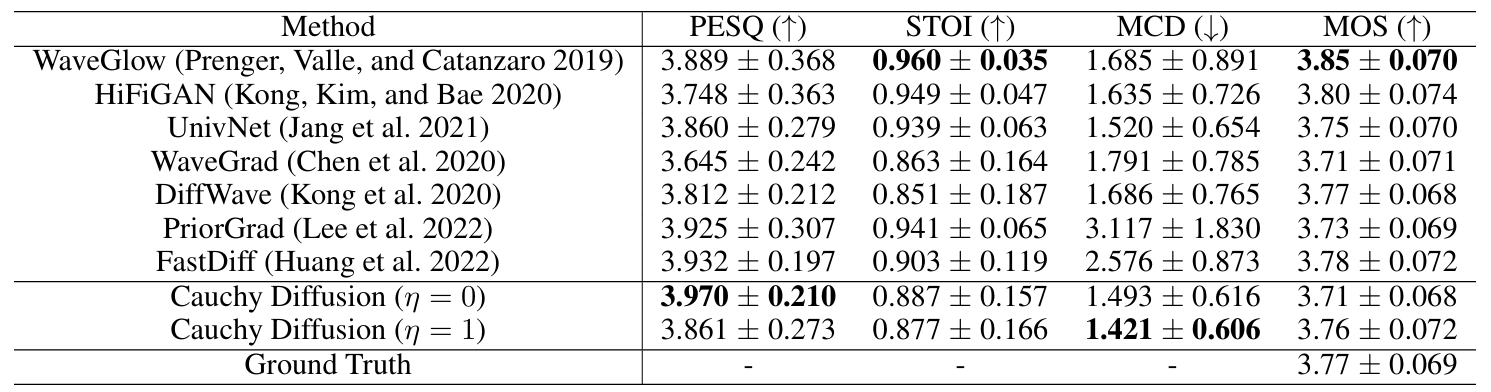
- Noise Clamp Value (NCV)
- NCV가 클수록 model convergence가 느려짐
- 특히 large NCV model은 small NCV model 보다 열등한 성능을 보이므로, Cauchy noise value를 적절히 clamping 하는 것이 필요함
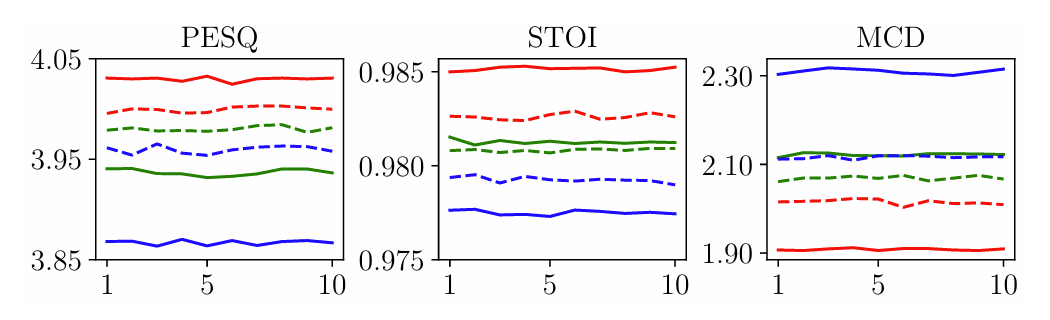
- Ablation Study
- Cauchy Diffusion은 $\eta=1,\text{NCV}=5, \lambda=10, T=1000$일 때 최적의 성능을 달성함
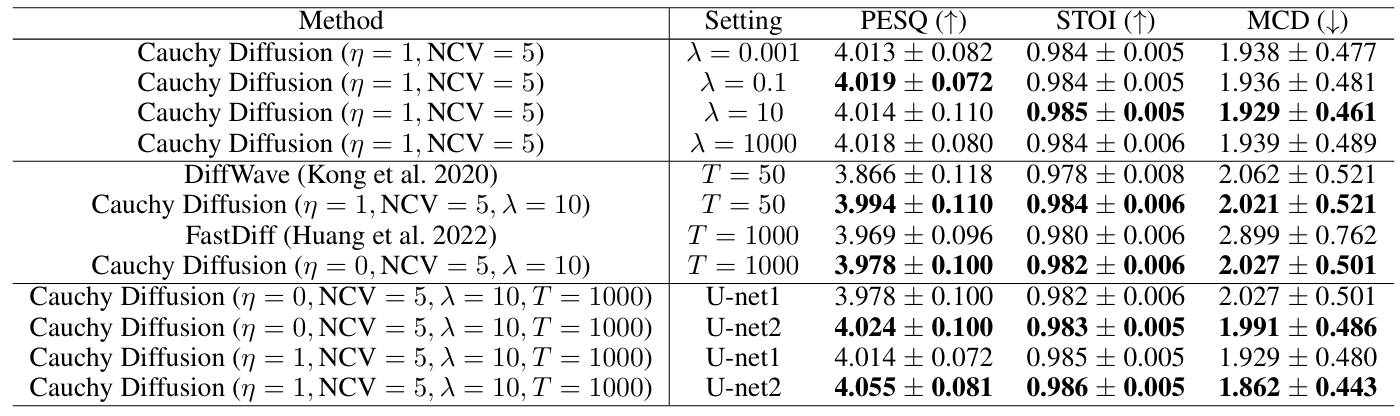
반응형
'Paper > Vocoder' 카테고리의 다른 글
댓글
