티스토리 뷰
Paper/Vocoder
[Paper 리뷰] WaveFM: A High-Fidelity and Efficient Vocoder based on Flow Matching
feVeRin 2025. 3. 30. 12:44반응형
WaveFM: A High-Fidelity and Efficient Vocoder based on Flow Matching
- Flow Matching은 diffusion model에 대한 robust training을 제공하지만 neural vocoder에 directly applying 하면 audio quality가 저하됨
- WaveFM
- Standard Gaussian prior 대신 mel-conditioned prior distribution을 채택하여 transportation cost를 minimize
- Refined multi-resolution STFT loss를 결합하여 audio quality를 향상
- 추가적으로 inference speed 향상을 위해 consistency distillation method를 적용
- 논문 (NAACL 2025) : Paper Link
1. Introduction
- Real-time high-fidelity speech synthesis를 위해 Flow-based, Generative Adversarial Network (GAN)-based, Diffusion-based model과 같은 non-autoregressive model이 주로 활용됨
- Flow-based model은 WaveFlow, WaveGlow와 같이 selected prior distribution에서 waveform을 생성하기 위해 invertible nerual network를 활용하여 log-likelihood를 estimate 하는 방식을 사용함
- BUT, invertibility와 determinant evaluation으로 인해 flexibility의 한계가 있음 - MelGAN, HiFi-GAN, BigVGAN과 같은 GAN-based model은 large receptive field와 다양한 discriminator를 활용해 high-fidelity speech를 생성할 수 있음
- 한편으로 DiffWave, BDDM, FreGrad 등은 Denoising Diffusion Probabilistic Model (DDPM)에 기반한 parameter-free noise-adding diffusion process를 활용하여 high-fidelity speech를 생성함
- BUT, diffusion model은 training 중에 discriminator와 같은 auxiliary network가 필요하지 않다는 장점이 있지만 inference phase가 상당히 time-consuming 하다는 단점이 있음
- 한편으로 Consistency Model은 각 step에서 Probability Flow-Ordinary Differential Equation (PF-ODE)의 endpoint를 directly predict 하는 방식으로 single-step inference를 지원할 수 있음
- 즉, ODE trajectory를 따라 align 하여 higher distillation efficiency를 달성할 수 있으므로 entire ODE를 numerically solve 할 필요가 없음
- Flow-based model은 WaveFlow, WaveGlow와 같이 selected prior distribution에서 waveform을 생성하기 위해 invertible nerual network를 활용하여 log-likelihood를 estimate 하는 방식을 사용함
-> 그래서 consistency distillation을 통해 efficient diffusion-based speech synthesis를 지원하는 WaveFM을 제안
- WaveFM
- Mel-spectrogram에 대한 appropiratly conditioned distribution을 활용하여 sample quality를 개선
- Waveform을 directly predict 하는 reparameterized flow matching method를 채택하고 auxiliary loss를 적용해 model 성능을 향상
- 특히 phase angle에 대한 model output을 supervise 하는 multi-resolution phase loss를 integrate 함
- Gradient, Laplacian operator를 real/generated spectrogram에 적용해 spectrogram에서 edge detail과 structural pattern을 효과적으로 반영함
- 추가적으로 tailored consistency distillation method를 통해 audio quality는 유지하면서 inference speed를 further accelerate
< Overall of WaveFM >
- Consistency Distillation과 Flow Matching을 활용한 efficient, high-fidelity vocoder
- 결과적으로 기존 diffusion-based model 보다 더 우수한 합성 품질과 빠른 inference speed를 달성
2. Background
- Flow Matching and Rectified Flow Models
- Flow Matching과 Rectified Flow는 similar training objective를 share 하고 diffusion model도 해당 framework 내에서 interpret 될 수 있음
- [Theorem 1] $x_{t}$를 $t\in[0,1]$에 대한 continuously differentiable random process, $p(x,t)$를 probability density function이라고 하자. Prior distribution을 $x_{0}$, ground-truth를 $x_{1}$이라고 할 때, conditional expectation $\mathbb{E}\left[\left.\frac{\text{d}x_{t}}{\text{d}t}\right|x_{t}=x\right]$이 locally Lipschitz라면:
(Eq. 1) $v(x,t)=\mathbb{E}\left[\left.\frac{\text{d}x_{t}}{\text{d}t}\right|x_{t}=x\right]$
이다. - 그러면 data distribution $x_{1}$의 sample은 prior distribution $x_{0}$에서 sampling 한 다음, time $t=0$에서 initial value $x_{0}$를 사용하여 다음의 ODE를 solve 하여 얻어짐:
(Eq. 2) $\frac{\text{d}x}{\text{d}t}=v(x,t)$ - 여기서 conditional expectation은 simple Mean Square training objective로 나타낼 수 있음:
(Eq. 3) $\min_{v}\mathbb{E}\left|\left| \frac{\text{d}x_{t}}{\text{d}t}-v(x_{t},t)\right|\right|^{2}$ - 일반적으로 straight trajectory는 lower transportation cost를 의미하므로, neural network $v(x,t)$에 대한 다음 objective로 이어짐:
(Eq. 4) $x_{t}=tx_{1}+(1-t)x_{0}, \,\,\, t\in[0,1]$ - Training process 이후 data sample은 [Theorem 1]에 따라 ODE를 numerically solve 하여 얻어짐:
(Eq. 5) $\min_{v}\mathbb{E}\left|\left|x_{1}-x_{0}-v(x_{t},t)\right|\right|^{2}$
- [Theorem 1] $x_{t}$를 $t\in[0,1]$에 대한 continuously differentiable random process, $p(x,t)$를 probability density function이라고 하자. Prior distribution을 $x_{0}$, ground-truth를 $x_{1}$이라고 할 때, conditional expectation $\mathbb{E}\left[\left.\frac{\text{d}x_{t}}{\text{d}t}\right|x_{t}=x\right]$이 locally Lipschitz라면:
- Consistency Distillation
- Consistency Distillation (CD)는 diffusion model을 distillating 하여 one-step generation을 지원함
- 기존에는 다음의 forward Stochastic Differential Equation (SDE)를 통해 data를 diffuse 함:
(Eq. 6) $\text{d}x=\sqrt{2t}\text{d}w,\,\,\,t\in[\epsilon ,T]$
- $\epsilon=0.002$, $T=80$ - 이때 backward SDE와 PF-ODE는:
(Eq. 7) $\text{d}x=-2t\nabla_{x}\log p(x,t)\text{d}t+\sqrt{2t}\text{d}w$
(Eq. 8) $\text{d}x=-t\nabla_{x}\log p(x,t)\text{d}t$ - 한편으로 CD에서 time step은 다음과 같이 discretize 됨:
(Eq. 9) $t_{i}=\epsilon^{1/\rho}+\frac{i-1}{N-1}(T^{1/\rho}-\epsilon^{1/\rho})$
- $N$ : total discretization step 수, $\rho=7$, $i\in\{1,...,N\}$ - Forward SDE에 따라,
- CD는 $n\in\mathcal{U}\{1,2,...,N-1\}, x_{t_{n+1}}\sim\mathcal{N}(x_{\text{clean}},t^{2}_{n+1}I)$를 sample 하고 pre-trained teacher score network를 사용하여 PF-ODE를 numerically solve 해 $\hat{x}_{t_{n}}$을 얻음
- 이를 위해 ODE solver를 채택할 수 있음 - CD student network는 any position/time에서 PF-ODE trajectory의 time $t=\epsilon$에서 endpoint를 predict 하는 것을 목표로 함:
(Eq. 10) $f_{\theta}(x,t)=c_{\text{skip}}(t)x+c_{\text{out}}(t)F_{\theta}(x,t)$
- $c_{\text{skip}}(t)=\frac{\sigma^{2}_{\text{data}}}{(t-\epsilon )^{2}+\sigma_{\text{data}}^{2}}, c_{\text{out}}=\frac{\sigma_{\text{data}}(t-\epsilon )}{\sqrt{\sigma_{\text{data}}^{2}+t^{2}}}$
- $\sigma_{\text{data}}=0.5$, $F_{\theta}(x,t)$ : neural network - 그러면 CD의 loss function은:
(Eq. 11) $\lambda(t_{n})d\left(f_{\theta}(x_{t_{n+1}},t_{n+1}),f_{\theta^{-}}(\hat{x}_{t_{n}},t_{n})\right)$
- $\lambda(t_{n})$ : scale function, $d(\cdot, \cdot)$ : $L2$ distance와 같은 distance function - Parameter $\theta^{-}$는 Exponential Moving Average (EMA)를 통해 update 됨:
(Eq. 12) $\theta^{-}\leftarrow \text{stopgrad}(\mu\theta^{-}+(1-\mu)\theta)$
- $\mu$ : EMA decay rate
- CD는 $n\in\mathcal{U}\{1,2,...,N-1\}, x_{t_{n+1}}\sim\mathcal{N}(x_{\text{clean}},t^{2}_{n+1}I)$를 sample 하고 pre-trained teacher score network를 사용하여 PF-ODE를 numerically solve 해 $\hat{x}_{t_{n}}$을 얻음
- 기존에는 다음의 forward Stochastic Differential Equation (SDE)를 통해 data를 diffuse 함:
3. Method
- Mel-Conditioned Prior Distribution
- PriorGrad, SpecGrad와 같이 mel-conditioned prior distribution은 diffusion model에서 자주 활용되지만, 실제로는 diffusion training objective stabilizing으로 인해 audio distribution에 approximate 하지 못함
- 대표적으로 PriorGrad는 $\mathcal{N}(\mu,\Sigma)$를 diffusion prior distribution으로 사용하고, 이때 training objective는:
(Eq. 13) $x_{t}=\sqrt{\bar{\alpha}_{t}}(x_{0}-\mu)+\sqrt{1-\bar{\alpha}_{t}^{2}}\epsilon $
(Eq. 14) $\min_{\epsilon}(\epsilon -\epsilon (x_{t},t))^{\top}\Sigma^{-1}(\epsilon -\epsilon_{\theta}(x_{t},t))$
- $x_{0}\sim p_{\text{data}}$,$\epsilon\sim\mathcal{N}(0,\Sigma)$
- $\mu=0$, $\Sigma$ : mel-spectrogram에서 derive 된 diagonal matrix - 해당 training process를 stabilize 하기 위해서는 standard deviation을 $[0.1,1]$로 clamp 해야 하므로, prior와 audio distribution 간의 distance가 증가함
- BUT, [Theorem 1]에 따라 flow matching model training은 analytical form 없이 2개의 marginal distribution에서 sampling을 수행하기만 하면 됨 - 즉, WaveFM은 training stability를 compromise 하지 않고도 smaller variance의 prior distribution을 활용할 수 있음
- 먼저 diagonal $\Sigma$를 가지는 prior distribution $\mathcal{N}(0,\Sigma)$를 choice 하자
- 이때 raw value가 $[0,32768]$의 wide range에 span 되어 있으므로 neural network의 input으로 logarithmic mel-spectrogram을 사용함
- Mel-spectrogram은 audio signal의 energy를 capture 하므로 frequency dimension에 대한 summation의 square root는 prior distribution의 standard deviation으로 적합함 - 다음으로 $[0,1]$ 내에 위치시키기 위해 $\sqrt{\text{mel-bands}\times 32768}$로 divide 하여 normalize 하고 linear interpolation을 적용하여 audio shape에 align 함
- Minimum value는 $10^{-3}$으로 clamp 됨
- Mel-spectrogram value는 일반적으로 potential maximum value보다 훨씬 smaller 하므로 standard deviation은 nearly silent region에서 $10^{-3}$에 approach 할 수 있음
- 결과적으로 이는 WaveFM의 prior distribution이 audio distribution과 closely align 되어 있음을 의미함
- 대표적으로 PriorGrad는 $\mathcal{N}(\mu,\Sigma)$를 diffusion prior distribution으로 사용하고, 이때 training objective는:
- Training Objective
- (Eq. 5)의 original objective는 random derivative를 estimate 하는 것을 목표로 하므로, mel-spectrogram loss와 같은 auxiliary loss의 incorporation을 어렵게 함
- 나아가 random noise의 periodic pattern distrubing으로 인해 periodic inductive bias를 포함하는 neural network를 사용하지 못함
- 특히 경험적으로 해당 original objective는 sample quality를 저해함 - 반면 WaveFM은 neural network가 random derivative를 predict 하는 대신 noise로부터 audio를 directly generate 하는 것을 목표로 함
- 따라서 논문은 original Mean Square obejctive를 다음과 같이 reparameterize 함:
(Eq. 15) $x_{1}-x_{0}=\frac{x_{1}-x_{t}}{1-t},\,\,\,t\in[0,1)$
(Eq. 16) $v(x_{t},t)=\mathbb{E}[x_{1}-x_{0}|x_{t}]=\frac{\mathbb{E}[x_{1}|x_{t}]-x-{t}}{1-t}$
(Eq. 17) $\Leftrightarrow \min_{v'}\frac{\mathbb{E}||x_{1}-v'(x_{t},t)||^{2}}{1-t},\,\,\,t\in[0,1)$ - 이를 기반으로 neural network는 GAN과 유사하게 mel-spectrogram에서 clean audio를 predict 할 수 있고, 다음의 auxiliary loss를 straight-forward add 할 수 있음:
(Eq. 18) $\min_{v'}\left(\frac{1}{1-t}\mathbb{E}|| x_{1}-v'(x_{t},t)||^{2}+\lambda_{0}\mathbb{E}[\text{STFTLoss}(x_{1},v'(x_{t},t))]+\lambda_{1}\mathbb{E} \frac{|| \text{mel}(x_{1})-\text{mel}(v'(x_{t},t))||_{1}}{M}\right)$
- $\lambda_{0}=0.02, \lambda_{1}=0.02$, $M$ : mel-spectrogram의 element 수
- $\frac{1}{1-t}$에서 infinity approaching을 방지하기 위해 coefficient를 $t\in[0.9,1)$에 대해 10으로 설정
- 따라서 논문은 original Mean Square obejctive를 다음과 같이 reparameterize 함:
- First auxiliary loss는 Parallel WaveGAN의 multi-resolution STFT loss로써, clean/generated audio의 3가지 resolution에 대해 STFT를 적용하여 얻어짐
- 여기서 FFT, hop, window size는 각각 $(1024,2048,512), (120,240,50), (600,1200,240)$
- 한편으로 spectral convergence loss $\mathcal{L}_{\text{sc}}$와 log-STFT magnitude loss $\mathcal{L}_{\text{mag}}$는:
(Eq. 19) $\mathcal{L}_{\text{sc}}(x,\hat{x})=\frac{||\,|\text{STFT}(x)|-|\text{STFT}(\hat{x})| \, ||_{F}}{|| \,|\text{STFT}(x)|\, ||_{F}}$
(Eq. 20) $\mathcal{L}_{\text{mag}}(x,\hat{x})=\frac{1}{N}\left|\left| \log \frac{|\text{STFT}(x)|}{|\text{STFT}(\hat{x})|}\right|\right|_{1}$
- $x, \hat{x}$ : clean/generated audio, $N$ : STFT spectrogram의 element 수
- $||\cdot||_{F},||\cdot||_{1}$ : 각각 Frobenius norm, $L1$ norm
- Norm 내의 STFT-shaped matrix에 대한 operator는 element-wise로 동작함 - 결과적으로 total loss function은:
(Eq. 21) $\text{STFTLoss}(x,\hat{x})=\frac{1}{3}\sum_{m=1}^{3}(\mathcal{L}_{\text{sc}}^{(m)}+\mathcal{L}_{\text{mag}}^{(m)})(x,\hat{x})$ - 여기서 original multi-resolution STFT loss는 STFT spectrogram의 magnitude information 만을 사용하므로, $\mathcal{L}_{\text{sc}}$를 phase angle loss $\mathcal{L}_{\text{pha}}$로 replace 함:
(Eq. 22) $\Delta P=\text{Phase}(\text{STFT}(x))-\text{Phase}(\text{STFT}(\hat{x}))$
(Eq. 23) $\mathcal{L}_{\text{pha}}(x,\hat{x})=\frac{|| \text{atan2}(\sin\Delta P, \cos\Delta P)||_{1}}{N}$
- $\text{atan2}$ : phase difference를 $(-\pi,\pi]$로 wrapping 하는 역할 - 이때 phase angle은 excessively large gradient를 생성할 수 있으므로, squared magnitude가 $1\times 10^{-6}$ 보다 작은 phase angle loss는 compute 하지 않음
- 추가적으로 $\mathcal{L}^{(m)}_{\text{mag}}$를 compute 하기 위해 squared magnitude에 $1\times 10^{-6}$의 small constant를 add 하고, FFT, hop, window size를 각각 $(1024, 2048, 512), (128, 256, 64), (512, 1024, 256)$으로 adjust 함
- 최종적으로 multi-resolution STFT loss를 더욱 향상하기 위해 clean/generated spectrogram magnitude에 temporal gradient, frequency gradient, Laplacian operator를 적용함:
(Eq. 24) $\displaystyle{ \frac{1}{4}\begin{bmatrix}
-1 & 1 \\
-2 & 2 \\
-1 & 1 \\
\end{bmatrix},\,\,\, \frac{1}{4}\begin{bmatrix}
-1 & -2 & -1 \\
1 & 2 & 1 \\
\end{bmatrix},\,\,\, \frac{1}{8}\begin{bmatrix}
-1 & -1 & -1 \\
-1 & 8 & -1 \\
-1 & -1 & -1 \\
\end{bmatrix}}$
- 이후 각각 $4,4,2$로 scale 된 mean squared error를 compute 하여 model이 spectrogram 내에서 regular pattern을 학습하도록 함
- 결과적으로 해당 operator를 통해 spectrogram의 edge information에 대한 visibility를 향상하여 finer detail을 효과적으로 capture 할 수 있음 - 실제로 앞선 multi-resolution STFT loss를 적용하면 WaveFM의 one-step generation quality를 개선할 수 있음
- 특히 아래 그림과 같이 original loss를 사용하여 생성된 spectrogram은 WaveFM의 spectrogram에 비해 lower accuracy를 보임 - 추가적으로 second auxiliary loss function으로 mel-spectrogram의 average $L1$ loss를 채택해 quality를 향상함
- 나아가 random noise의 periodic pattern distrubing으로 인해 periodic inductive bias를 포함하는 neural network를 사용하지 못함

- 한편으로 WaveFM의 reparameterization은 time $t=1$에서 diverge 함
- 따라서 논문은 distillation 과정에서 $t$의 range를 $[0,0.99]$로 restrict 함
- Waveform이 already sufficiently clean 하므로 large $t$는 효과적이지 않기 때문 - 결과적으로 WaveFM training은 [Algorithm 1]과 같이 수행됨
- $\text{prior}(m)$ : mel-spectrogram $m$에서 derive 된 diagonal covariance matrix
- $v_{\theta}$ : reparameterized $v'$
- 따라서 논문은 distillation 과정에서 $t$의 range를 $[0,0.99]$로 restrict 함

- Distillation Objective
- Numerical ODE solver를 사용하는 기존 inference method는 waveform 생성을 위해 상당한 step이 필요함
- 따라서 논문은 [Algorithm 2]와 같이 SDE에 대한 Consistency Distillation을 도입함
- 먼저 student network는 pre-trained model로 initialize 되고 student network parameter의 EMA를 계산하여 distillation procedure를 stabilizing 하는데 필요한 consistency training target을 생성함
- 이때 distillation process는 $\mathcal{U}(0,0.99)$가 아닌 $[0,0.99]$ range 내의 truncated $\mathcal{N}(0,0.33^{2})$에서 $t$를 sampling 함
- One-step generation에서 near $t=0$의 time step error가 더 critical 하기 때문
- 먼저 student network는 pre-trained model로 initialize 되고 student network parameter의 EMA를 계산하여 distillation procedure를 stabilizing 하는데 필요한 consistency training target을 생성함
- 한편으로 [Algorithm 2]에서 distance function $d(\cdot,\cdot)$은 network output과 target 간의 training loss를 의미하고, 앞선 결과와 같이 4개의 term으로 구성됨
- $\text{ODESOLVE}$의 경우, any numerical solver를 사용할 수 있음
- 논문은 Euler method를 채택 - 이때 original objective를 reparameterize 하므로 numerical ODE solver에 대한 original function을 reconstruct 할 수 있어야 함
- $\text{ODESOLVE}$의 경우, any numerical solver를 사용할 수 있음
- 논문은 consistency function을 continuously differentiable manner로 parameterizing 하지 않고, $1$에 close 한 time point에서 clean audio를 target으로 설정한 다음 neural network를 통해 smaller time point의 결과를 predict 함
- 이는 기존 consistency model과 같이 parameterize 하면 generated audio quality가 degraded 되기 때문 - 결과적으로 WaveFM의 consistency distillation은 dynamic prior distribution과 compatible 하므로, fixed prior distribution에 의존하는 기존 consistency model과는 달리 prior sampling만 필요함
- 따라서 논문은 [Algorithm 2]와 같이 SDE에 대한 Consistency Distillation을 도입함

- Network Architecture
- Function $v(x,t)$는 19.5M parameter의 asymmetric U-Net model을 기반으로 HiFi-GAN의 multi-receptive field module을 채택함
- ResBlock에서 Conv1D는 'same' padding을 사용하고, 각 ResLayer는 kernel list, dilation list로 정의됨
- 여기서 kernel list, dilation list의 outer product는 ResBlock matrix와 각 ResBlock의 convolutional layer에 대한 kernel width, dilation을 정의함 - Mel-spectrogram은 detailed condition을 제공하므로 neural network는 mel-spectrogram을 upsampling 하고 waveform을 step-by-step refine 해야 함
- 따라서 WaveFM은 U-Net upsampling process를 활용하고 larger kernel size를 가지는 dilated convolutional layer를 채택하여 mel-spectrogram으로부터 audio를 reconstrcut 함
- 반면 downsampling process는 simpler convolutional layer로 구성됨 - 결과적으로 아래 그림과 같이 $4\times 1$ ResBlock matrix를 포함하는 downsampling ResLayer와 $3\times 3$ ResBlock matrix를 포함하는 upsampling ResLayer를 구축함
- 따라서 WaveFM은 U-Net upsampling process를 활용하고 larger kernel size를 가지는 dilated convolutional layer를 채택하여 mel-spectrogram으로부터 audio를 reconstrcut 함
- Multi-receptive field module에서 channel-wise log-scale parameter $\alpha,\beta$로 정의된 snake-beta activation을 사용함:
(Eq. 25) $\text{snake}(x)=x+\frac{1}{e^{\beta}+\epsilon}\sin^{2}(e^{\alpha}x)$
- (Eq. 25)는 BigVGAN을 따름
- $\epsilon=10^{-8}$ : numerical stability를 위해 사용되는 value - Down/upsampling process는 각각 strided/transposed convolution을 사용함
- 해당 architecture를 통해 mel-spectrogram으로부터 waveform을 directly generate 함 - Time representation의 경우 $t\in[0,1]$을 100으로 scale 하여, diffusion model과 magnitude를 align 한 다음, 128-dimensional positional encoding vector에 embedding 함:
(Eq. 26) $\left[\sin\left(100t\cdot 10^{\frac{0\times 4}{63}}\right),..., \sin\left(100t\cdot 10^{\frac{63\times 4}{63}}\right),\cos\left(100t \cdot 10^{\frac{0\times 4}{63}}\right),..., \cos\left(100t \cdot 10^{\frac{63\times 4}{63}}\right)\right]$
- (Eq. 26)은 DiffWave를 따름
- 해당 128-dimensional time embedding은 2개의 linear-SiLU layer를 통해 512-dimension으로 expand 된 다음, 각 resolution을 desired shape로 reshape 하고, downsampling process에서 hidden layer에 add 됨
- ResBlock에서 Conv1D는 'same' padding을 사용하고, 각 ResLayer는 kernel list, dilation list로 정의됨

4. Experiments
- Settings
- Dataset : LibriTTS, MUSDB18-HQ
- Comparisons : HiFi-GAN, BigVGAN, DiffWave, PriorGrad, FreGrad, FastDiff
- Results
- LibriTTS dataset에 대해 WaveFM이 가장 뛰어난 성능을 보임

- MUSDB18-HQ dataset에 대해서도 WaveFM이 가장 우수함
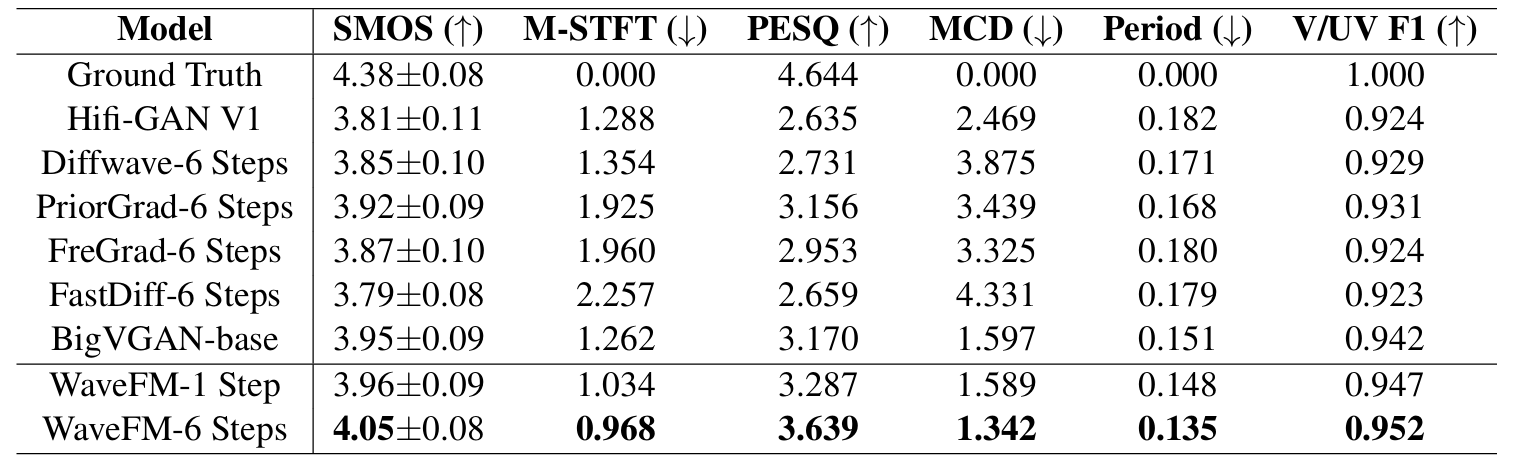
- WaveFM은 HiFi-GAN 수준의 Real Time Factor (RTF)를 달성할 수 있음

- Out-of-Distribution Situation
- WaveFM의 mel-spectrogram은 ground-truth와 더 closer 함
- 특히 PriorGrad는 low-frequency component를 overestimate 하고 BigVGAN은 clean spectrogram에서 regular component를 generate 하지 못함

- Ablation Study
- WaveFM의 각 component를 제거하는 경우 성능 저하가 발생함
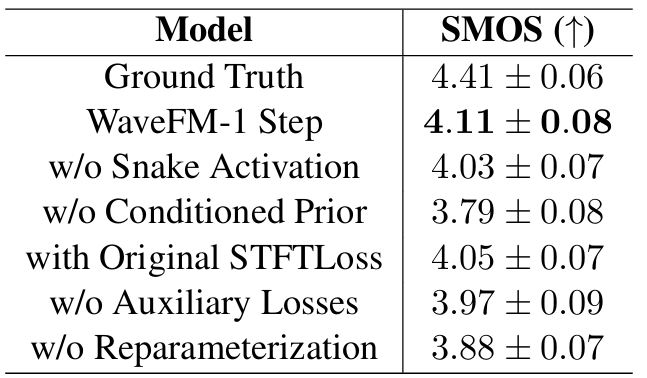
반응형
'Paper > Vocoder' 카테고리의 다른 글
댓글
