[Paper 리뷰] Vocos: Closing the Gap Between Time-domain and Fourier-based Neural Vocoders for High-Quality Audio Synthesis

Vocos: Closing the Gap Between Time-domain and Fourier-based Neural Vocoders for High-Quality Audio Synthesis

---

• 기존의 neural vocoder는 time-domain에서 동작하는 Generative Adversarial Network을 활용함
• BUT, 해당 방식은 time-frequency representation이 제공하는 inductive bias를 무시하므로 redundant, computationally-intense 한 upsampling operation이 요구됨
• Vocos
  • 더 빠른 계산과 human perception과의 align의 이점을 활용할 수 있는 Fourier-based time-frequency representation을 활용
  • Complex-valued spectrogram reconstruction 과정에서 발생하는 phase recovery 문제를 해결하기 위해, 모델이 Fourier spectral coefficient를 직접 생성하도록 함
• 논문 (ICLR 2024) : Paper Link

---

1. Introduction

• 기존의 neural vocoder는 time-domain에서 audio sample distribution을 모델링하여 음성 합성을 수행함
  • 이때 time-domain vocoder는 크게 autoregressive, non-autoregressive model로 나누어짐
    1. WaveNet과 같은 autoregressive model은 sample을 sequential 하게 생성하여, 이전에 생성된 모든 sample에 대해 새로운 sample을 conditioning 함
    2. Non-autoregressive model은 모든 sample을 independent 하게 생성하므로 parallelizing이 가능함
       - BUT, 이러한 time-domain audio 합성에서는 signal의 spectral representation을 생성하는 것이 어려움
  • 특히 Short-Time Fourier Transform (STFT)는 original signal을 완벽하게 reconstruct 하는 것이 가능하지만, 대부분의 경우에서 STFT의 magnitude만 사용하므로 information loss가 발생함
    - STFT의 magnitude는 duration 동안 다양한 frequency component의 amplitude를 explicit 하게 나타내지만, phase information은 비직관적이기 때문에 manipulation 시 unpredictable 한 결과를 발생시키기 때문
  • 따라서 phase distribution을 모델링하는 것은 time-frequency domain의 intricate nature로 인해 한계가 있음
    1. 아래 그림과 같이 phase spectrum은 periodic structure로 인해 $(-\pi,\pi]$ range 내에서 principal value를 wrapping 하게 만듦
       
    2. (b)와 같이 phase wrapping은 $-\pi$와 $\pi$ 주변에서 observe 되는 discontinuity를 발생시키지만, complex plane에서 해당 discontinuity는 continuous rotation을 나타냄
    3. (c)의 instantaneous phase는 $\varphi(t)=\arg\{\hat{s}(t)\}$로 계산됨
       - $\hat{s}(t)$ : $s(t)=\sin(\omega t)$의 Hilbert transform
  • BUT, 위의 어려움에도 불구하고 phase spectrum에 대한 효과적인 추정이 가능하면 audio에 대한 perceptual quality를 크게 향상할 수 있음

(a) Time-Varying Frequency (b) Phase Wrapping using Sinusoidal Signal (c) Instantaneous Phase

-> 그래서 audio 합성 성능 향상을 위해 Fourier-related coefficient 모델링을 generative model에 반영한 Vocos를 제안

 

• Vocos
  • Audio의 complex STFT coefficient를 생성하도록 train 된 Generative Adversarial Network (GAN)-based vocoder
    - Upsampling 시 transposed convolution을 사용하는 기존 time-domain vocoder와 달리, 모든 layer에 대해 동일한 feature temporal resolution을 유지하고 Inverse STFT (iSTFT)를 통해 upsampling을 수행함
  • Phase angle 추정을 위해 unit circle로 정의된 activation function을 채택
    - 이를 통해 implicit phase wrapping을 incorporate 하여 모든 phase angle에서 meaningful value를 보장함
  • Network 전체에 걸쳐 low temporal resolution을 유지하기 위해, 기존 time-domain vocoder에서 사용되는 dilated convolution 대신 ConvNeXt block을 도입함

< Overall of Vocos >

• Complex-valued spectrogram reconstruction 과정에서 발생하는 phase reconstruction 문제를 해결하기 위해, 모델이 Fourier spectral coefficient를 직접 생성하도록 함
• 이때 upsampling을 위해 time-frequency domain에 대한 iSTFT와 ConvNeXt block을 도입
• 결과적으로 기존 vocoder보다 뛰어난 합성 성능을 달성

2. Method

- Overview 

• Vocos는 GAN을 기반으로하여 generator의 target data distribution으로써 Fourier-based time-frequency representation을 사용함
  • 이때 Vocos는 transposed convolution을 사용하지 않고, 대신 iSTFT를 통해 upsampling을 수행함
    
    1. 기존 time-domain vocoder의 경우, transposed convolution으로 input feature를 target waveform의 resolution으로 변환하기 위해 수백 번의 upscaling이 요구됨
    2. 반면 Vocos는 iSTFT를 사용하므로 network 전체에 대해 동일한 temporal resolution을 유지하는 isotropic architecture를 활용할 수 있음
  • 특히 transposed convolution은 aliasing artifact를 발생시키므로, Vocos는 learnable upsampling layer를 제거하고 well-established iSTFT를 사용함으로써 original-scale waveform을 artifact 없이 reconstruction 할 수 있음
    - 여기서 mel-spectrogram을 audio signal로 변환할 때, temporal resolution은 STFT hop size로 결정됨
  • 결과적으로 Vocos는 다음의 STFT를 사용하여 time-frequency domain의 audio signal을 represent함:
    (Eq. 1) $\mathrm{STFT}_{x}[m,k]=\sum_{n=0}^{N-1}x[n]w[n-m]e^{-j2\pi kn/N}$
    - STFT는 signal의 successive windowed section에 Fourier transform을 적용함
    - 실제로 STFT는 window function이 time에 따라 hop 되어 만들어진 overlapping, windowed data의 frame에 대해 Fast Fourier Transform (FFT) sequence를 적용하여 계산됨
    

(a) 기존 Time-domain GAN Vocoder (b) Vocos

- Model

• Backbone
  • Vocos는 ConvNeXt를 generator의 backbone으로 사용함
  • 이를 위해 먼저 input feature를 hidden dimensionality로 embed 한 다음, 1D convolutional stack을 적용함
    - 이때 각 block은 depthwise convolution로 구성되고 pointwise convolution을 사용하여 feature를 더 높은 dimensionality로 project 하는 inverted bottleneck이 추가됨
  • GELU activation은 bottleneck 내에서 사용되고, 각 block 사이에는 Layer Normalization이 적용됨
• Head
  • Real-valued signal의 Fourier transform은 conjugate symmetric 하므로, single-side band spectrum만 사용하여 frame당 $n_{fft}/2+1$의 coefficient를 얻음
  • 여기서 phase, magnitude value를 output 하기 위해 model을 parameterize 하면, hidden-dim activation은 $n_{fft}/2+2$ channel을 사용하여 tensor $\mathbf{h}$에 project 되고 다음과 같이 split 됨:
    (Eq. 2) $\mathbf{m},\mathbf{p}=\mathbf{h}[1:(n_{fft}/2+1)],\mathbf{h}[(n_{fft}/2+2):n]$
    - Magnitude를 나타내기 위해 $\mathbf{m}$에 exponential function을 적용함: $M=\exp(\mathbf{m})$
  • $\mathbf{p}$의 cosine과 sine을 계산하여 각각 $\mathbf{x},\mathbf{y}$를 얻고, $\mathbf{p}$를 unit circle에 mapping 하면:
    (Eq. 3) $\mathbf{x}=\cos(\mathbf{p})$
    (Eq. 4) $\mathbf{y}=\sin(\mathbf{p})$
  • 최종적으로 complexed-value coefficient는 $\mathrm{STFT} = M\cdot (\mathbf{x}+j\mathbf{y})$로 얻어짐
    - 해당 formulation을 통해 임의의 real argument $\mathbf{p}$에 대해 phase angle $\varphi = \mathrm{atan2}(\mathbf{y},\mathbf{x})$를 express 할 수 있음
    - 결과적으로 $\varphi$가 desired range $(-\pi,\pi]$에 correctly wrapped 되도록 보장 가능
• Discriminator
  • HiFi-GAN의 Multi-Period Discriminator (MPD)와 UnivNet의 Multi-Resolution Discriminator (MRD)를 사용

- Loss

• Vocos의 training objective는 reconstruction loss, adversarial loss, feature matching loss로 구성됨
  • 이때 least squares GAN objective 대신 hinge loss를 활용함:
    (Eq. 5) $\ell_{G}(\hat{x})=\frac{1}{K}\sum_{k}\max(0,1-D_{k}(\hat{x}))$
    (Eq. 6) $\ell_{D}(x,\hat{x})=\frac{1}{K}\sum_{k}\max(0,1-D_{k}(x))+\max(0,1+D_{k}(\hat{x}))$
    - $D_{k}$ : $k$-th sub-discriminator 
    
  • 그러면 reconstruction loss $L_{mel}$은 ground-truth sample $x$와 합성된 sample $\hat{x}$간의 mel-scaled magnitude spectrogram의 $L1$ distance로 정의됨:
    $L_{mel}=|| \mathcal{M}(x)-\mathcal{M}(\hat{x})||_{1}$
    
  • Feature matching loss $L_{feat}$는 $k$-th sub-discriminator의 $l$-th feature map 간 distance의 평균으로 계산됨:
    $L_{feat}=\frac{1}{KL}\sum_{k}\sum_{l}|| D_{k}^{l}(x)-D_{k}^{l}(\hat{x})||_{1}$
    

3. Experiments

- Settings

• Dataset : LibriTTS 
• Comparisons : HiFi-GAN, iSTFTNet, BigVGAN

- Results

• Objective Evaluation
  • 거의 모든 metric에서 제안된 Vocos가 가장 우수한 성능을 보임
  • 추가적으로 ablation study 측면에서 다음을 비교해 보면,
    1. Vocos with Absolute Phase
       - $[-\pi, \pi]$ range로 scale 된 tanh nonlinearity를 사용해 phase angle을 예측하는 경우, phase에 periodic nature를 제공하지 못하므로 품질 저하가 발생함
       - 즉, Vocos의 implicit phase wrapping이 성능 개선에 효과적이라는 것을 의미
    2. Vocos with Snake Activation
       - BigVGAN과 같은 time-domain vocoder에서는 Snake activation이 효과적이지만 Vocos에서는 유의미한 개선을 보이지 못함
       - Snake activation은 time-domain에 periodicity를 반영하기 위해 사용되는데, Vocos는 Fourier basis function을 통해 periodicity를 충분히 explicit 하게 반영하고 있기 때문
    3. Vocos without ConvNeXt
       - ConvNeXt block을 dilated convolution이 있는 ResBlock으로 대체하는 경우 성능 저하가 발생함
       - 즉, Vocos에서 ConvNeXt block은 성능 향상에 유효함

정량적 성능 비교

• Subjective Evaluation
  • MOS, SMOS 측면에서도 제안된 Vocos는 뛰어난 성능을 보임

정성적 성능 비교

• Out-of-Distribution Data
  • Unseen acoustic condition에 대한 generalizability를 확인해 보기 위해, MUSDB18 dataset에 대한 평가를 수행
  • 결과적으로 Vocos는 out-of-distribution data에 대해서도 우수한 합성 성능을 달성함
  • Mel-sepctrogram 측면에서 Vocos는 artifact 없이 harmonics를 더 정확하게 reconstruction 하는 것으로 나타남

MUSDB18에 대한 성능 비교

Mel-Spectrogram 비교

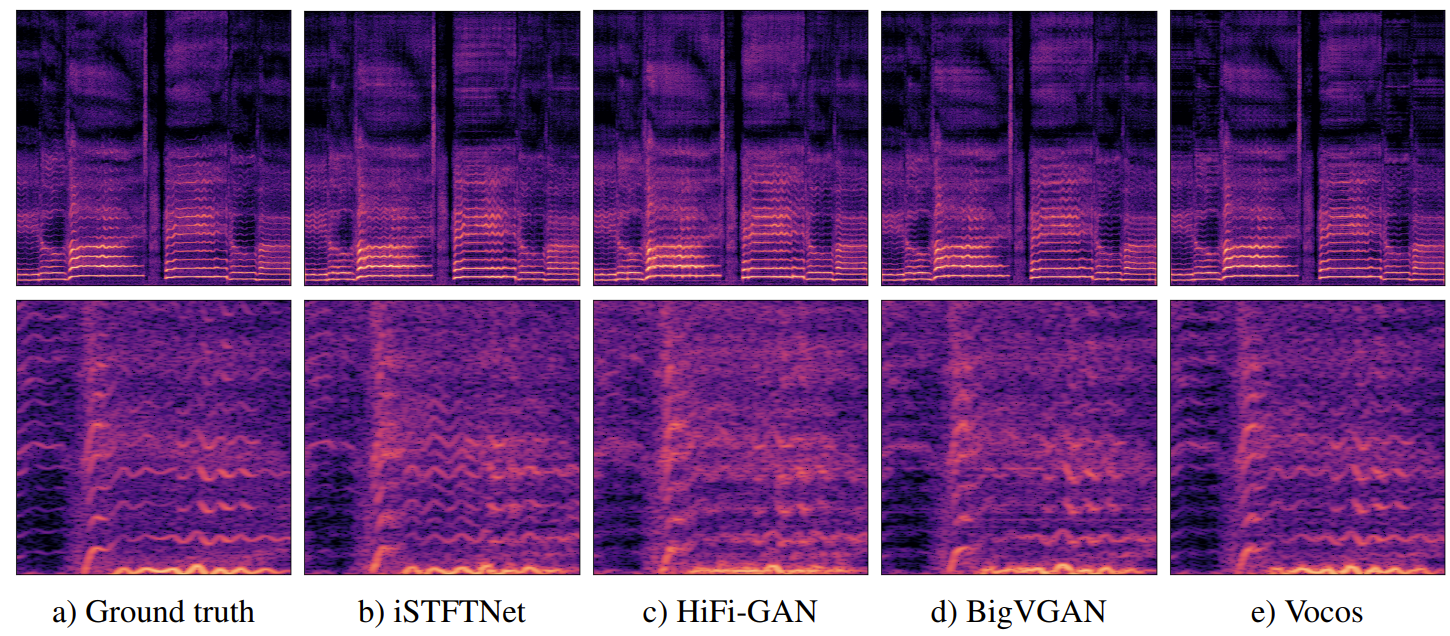
• Audio Reconstruction
  • 추가적으로 neural codec과 audio reconstruction 성능을 비교해 보면
  • Vocos는 EnCodec 보다 다양한 bandwidth에서 더 뛰어난 reconstruction 성능을 보임

다양한 bandwidth에 대한 정량적 성능 비교

다양한 bandwidth에 대한 정성적 성능 비교

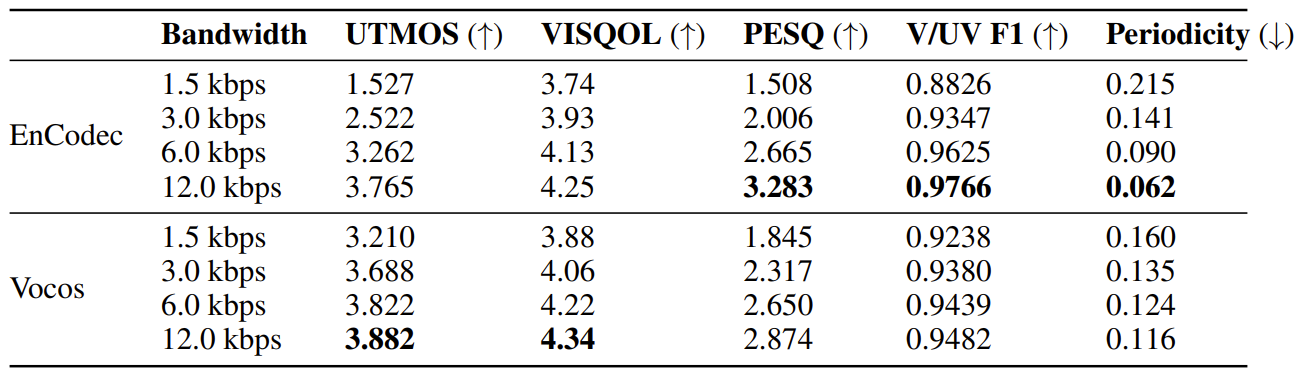
• Inference Speed
  • 추론 속도 측면에서 Vocos는 HiFi-GAN 보다 13배, BigVGAN 보다 70배 빠르게 동작할 수 있음
  • 이는 transposed convolution 대신 iSTFT를 사용하기 때문
  • 한편으로 Vocos의 ConvNeXt block을 depthwise separable convolution으로 대체하는 경우 추가적인 속도 향상을 달성할 수 있음

추론 속도 비교