티스토리 뷰
Paper/Vocoder
[Paper 리뷰] RNDVoC: Learning Neural Vocoder from Range-Null Space Decomposition
feVeRin 2025. 10. 1. 17:00반응형
RNDVoC: Learning Neural Vocoder from Range-Null Space Decomposition
- Neural vocoder는 parameter-performance trade-off가 존재함
- RNDVoC
- Range-Null Decomposition과 vocoder task를 bridge 하여 target spectrogram reconstruction을 range-space와 null-space 간의 superimposition으로 decompose
- 추가적으로 sub-band, sequential modeling을 위해 cross-/narrow-band module을 활용한 dual-path framework를 구성
- 논문 (IJCAI 2025) : Paper Link
1. Introduction
- Vocoder는 audible time-domain waveform을 reconstruct 하는 것을 목표로 함
- 특히 MelGAN, HiFi-GAN과 같은 non-autoregressive Generative Adversarial Network (GAN)-based vocoder는 reconstruction 측면에서 우수한 성능을 달성함
- 최근의 Vocos와 같은 time-frequency (T-F) domain-based vocoder는 inference speed를 크게 향상함
- BUT, 해당 neural vocoder는 다음의 한계점을 가지고 있음:
- Parameter-performance trade-off
- 대표적으로 BigVGAN은 우수한 성능에도 불구하고 112M의 상당한 parameter 수를 가짐
- Black-box modeling으로 인해 mel-spectrogram의 linear degradation을 neglect 하기 때문 - T-F domain vocoder는 inference efficency의 장점이 있지만 합성 품질이 낮음
- Acoustic feature는 specific frequency region에 존재하지만, T-F domain vocoder의 full-band modeling으로 인해 T-F spectrum의 hierarchical characteristic이 neglect 되기 때문
- Parameter-performance trade-off
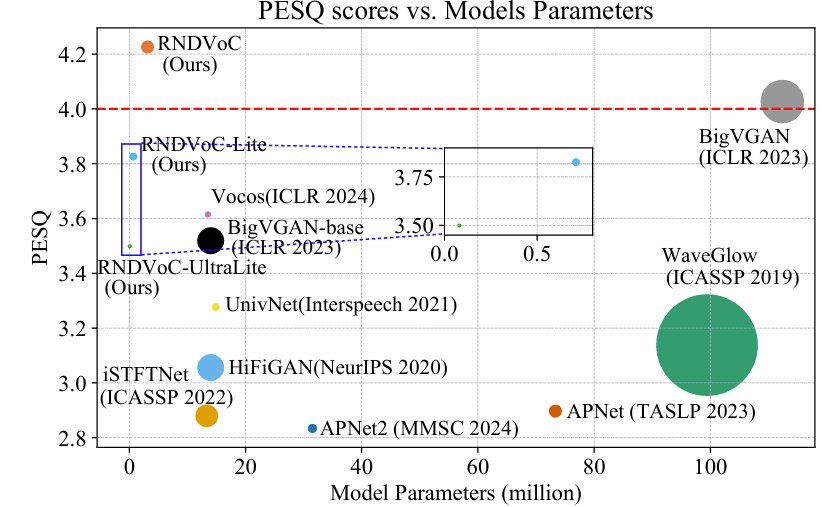
-> 그래서 T-F domain vocoder의 한계점을 개선한 RNDVoC를 제안
- RNDVoC
- Mel-spectrogram formulation을 Range-Null Decomposition (RND) theory와 연결
- Target spectrum reconstruction을 Range-Space Modeling (RSM), Null-Space Modeling (NSM)으로 decompose 함 - 추가적으로 dual-path structure를 통해 sub-band, sequential modeling을 지원
- Mel-spectrogram formulation을 Range-Null Decomposition (RND) theory와 연결
< Overall of RNDVoC >
- RND theory를 활용한 T-F domain neural vocoder
- 결과적으로 기존보다 더 적은 parameter로 더 나은 합성 품질을 달성
2. Method
- Range-Null Space Decomposition
- Range-Null Decomposition (RND)는 다음과 같이 formulate 됨
- Classical signal compression physical model의 경우:
(Eq. 1) $ \mathbf{y}=\mathbf{Ax}+\mathbf{n}$
- $\mathbf{x}\in\mathbb{R}^{D}, \{\mathbf{y}, \mathbf{n}\}\in\mathbb{R}^{d}$ : 각각 target, observed, noise signal
- $\mathbf{A}\in\mathbb{R}^{d\times D}$ : compression matrix, $d\ll D$ - Noise-free scenario에서 (Eq. 1)은 $\mathbf{y}=\mathbf{Ax}$로 simplify 될 수 있음
- $\mathbf{A}$의 pseudo-inverse $\mathbf{A}^{\dagger}\in\mathbb{R}^{D\times d}$가 $\mathbf{AA}^{\dagger}\mathbf{A}\equiv \mathbf{A}$를 만족하면, $\mathbf{x}$는 2개의 orthogonal subspace로 decompose 됨:
(Eq. 2) $\mathbf{x}\equiv\mathbf{A}^{\dagger}\mathbf{Ax}+(\mathbf{I}-\mathbf{A}^{\dagger}\mathbf{A})\mathbf{x}$
- 이때 하나는 $\mathbf{A}$의 range-space에 속하고 다른 하나는 null-space에 속함
- $\mathbf{A}^{\dagger}\mathbf{Ax}$ : range-space component, $(\mathbf{I}-\mathbf{A}^{\dagger}\mathbf{A})\mathbf{x}$ : remaining null-space component - $\mathbf{x}$의 practical solution $\tilde{\mathbf{x}}$는 2가지 consistency condition을 만족해야 함:
- Degradation Consistency $\mathbf{A}\tilde{\mathbf{x}}\equiv \mathbf{y}$
- Compressed signal space에 embed 된 original information은 reconstruction 이후에도 unalter 되어야 함 - Data Consistency $\tilde{\mathbf{x}}\sim p(\mathbf{x})$
- Estimation $\tilde{x}$는 $\mathbf{x}$와 동일한 data distribution을 가져야 함
- Degradation Consistency $\mathbf{A}\tilde{\mathbf{x}}\equiv \mathbf{y}$
- 앞선 constraint를 기반으로 solution은 다음과 같이 얻어짐:
(Eq. 3) $\tilde{\mathbf{x}}\equiv\mathbf{A}^{\dagger}\mathbf{y}+(\mathbf{I}-\mathbf{A}^{\dagger}\mathbf{A})\hat{\mathbf{x}}$
- $\mathbf{A}^{\dagger}\mathbf{y}, (\mathbf{I}-\mathbf{A}^{\dagger}\mathbf{A})\hat{\mathbf{x}}$ : 각각 range-space, null-space - 이때 orthogonality로 인해 $\tilde{\mathbf{x}}$는 first condition $\mathbf{A}\tilde{\mathbf{x}}\equiv \mathbf{AA}^{\dagger}\mathbf{Ax}+\mathbf{A}(\mathbf{I}-\mathbf{A}^{\dagger}\mathbf{A})\hat{\mathbf{x}}\equiv\mathbf{Ax}+\mathbf{0}\equiv \mathbf{y}$를 만족함
- 따라서 second condition을 만족하기 위해서는 learnable network로 implement 되는 $\hat{\mathbf{x}}$의 estimation만 고려하면 됨
- Classical signal compression physical model의 경우:

- Revisit Neural Vocoder Tasks
- 논문에서는 vocoder의 acoustic feature로 mel-spectrogram을 채택함
- 먼저 log-scale mel-spectrogram의 degradation process는:
(Eq. 4) $ \mathbf{X}^{mel}=\log (\mathcal{A}|\mathbf{S}|)$
- $\mathbf{X}^{mel}\in\mathbb{R}^{F_{m}\times T}, |\mathbf{S}|\in\mathbb{R}^{F\times T}$ : 각각 mel, target spectrogram
- $\{F_{m},F\}$ : 각각 mel-/linear-scale의 frequency size, $T$ : frame size, $\mathcal{A}\in\mathbb{R}^{F_{m}\times F}$ : mel-filter - (Eq. 4)는 phase information discarding과 linear operation을 통한 magnitude compression의 2가지 degradation operation을 포함하고 있음
- 따라서 inverse process에는 phase spectrum estimation, compressed observation으로부터의 magnitude spectrum recovering이 포함됨 - 특히 기존 vocoder에서 neural network는 black-box로 동작하고, 다음과 같이 target waveform/T-F spectrum과 mel-feature 간의 relation을 establish 함:
(Eq. 5) $\tilde{\mathbf{s}}=\mathcal{F}_{T}(\mathbf{X}^{mel},\Theta_{1}),\,\,\, \left\{|\tilde{\mathbf{s}}|,\tilde{\Phi}\right\}=\mathcal{F}_{TF}(\mathbf{X}^{mel},\Theta_{2})$
- $\mathcal{F}_{T}(\cdot,\Theta_{1}), \mathcal{F}_{TF}(\cdot, \Theta_{2})$ : 각각 time-domain, T-F domain neural vocoder의 mapping function
- $\tilde{\mathbf{s}}$ : estimated time-domain waveform, $\{|\tilde{\mathbf{S}}|, \tilde{\Phi}\}$ : 각각 estimated spectral magnitude, phase - (Eq. 4)에서 $\bar{\mathbf{X}}^{mel}=\exp(\mathbf{X}^{mel})=\mathcal{A}|\mathbf{X}|$와 같이 log-operation이 absorb 되는 경우, (Eq. 1)의 noise-free case와 유사한 format을 가짐
- 즉, original magnitude spectrum recovery는 classical Compressive Sensing (CS)으로 formulate 할 수 있음
- 여기서 논문은 linearly-compressed representation으로부터 target signal을 reconstruct 함 - 결과적으로 (Eq. 3)의 explicit decomposition을 따라 (Eq. 5)의 target spectrum generation을 rewrite 하면:
(Eq. 6) $ |\tilde{\mathbf{S}}|_{range}=\mathcal{F}_{range}(\bar{\mathbf{X}}^{mel})=\mathcal{A}^{\dagger}\bar{\mathbf{X}}^{mel}$
(Eq. 7) $ \left\{|\tilde{\mathbf{S}}|_{null},\tilde{\Phi}\right\}=\mathcal{F}_{null}\left(|\tilde{\mathbf{S}}|_{range}\right)$
(Eq. 8) $ |\tilde{\mathbf{S}}|=|\tilde{\mathbf{S}}|_{range}+(\mathbf{I}-\mathcal{A}^{\dagger}\mathcal{A}) |\tilde{\mathbf{S}}|_{null}$
$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, =\mathcal{A}^{\dagger}\mathcal{A}|\mathbf{S}|+(\mathbf{I}-\mathcal{A}^{\dagger}\mathcal{A}) |\tilde{\mathbf{S}}|_{null}$
(Eq. 9) $\tilde{\mathbf{S}}=|\tilde{\mathbf{S}}|e^{j\tilde{\Phi}}$
- $\mathcal{F}_{range}(\cdot), \mathcal{F}_{null}(\cdot)$ : 각각 range-/null-space, $\mathcal{A}^{\dagger}\in\mathbb{R}^{F\times F_{m}}$ : $\mathcal{A}$의 pseudo-inverse - $\mathcal{F}_{range}$에서는 mel-domain의 original acoustic feature가 pseudo-inverse operation을 통해 target domain으로 transform 됨
- $\mathcal{F}_{null}$에서는 remaining magnitude detail이 estimate 되어 overall spectral reconstruction을 supplement 함
- 즉, original magnitude spectrum recovery는 classical Compressive Sensing (CS)으로 formulate 할 수 있음
- 기존 방식과 비교하여 (Eq. 8)의 reconstruction은 다음의 장점을 가짐:
- Mel-spectrum의 linear degradation을 prior로 fully utilize 하여 2개의 orthogonal sub-space를 establish 함으로써 overall framework의 interpretability를 향상함
- Degradation consistency로 인해 mel-spectrogram에 embed 된 original acoustic feature를 well-preserve 할 수 있으므로 reconstructed signal의 acoustic distortion을 mitigate 할 수 있음
- 이때 spectral magnitude 만이 degradation formulation에 involve 하므로 논문은 (Eq. 7)과 같이 phase component를 estimate 하기 위해 $\mathcal{F}_{null}$을 enforce 함
- 특히 empirical trick으로 pseudo-inverse strategy를 활용하는 FreeV와 달리, 논문의 pseudo-inverse operation은 intuitive physical explanation을 endow 할 수 있음
- 먼저 log-scale mel-spectrogram의 degradation process는:
- Architecture Design of RNDVoC
- 논문은 2개의 orthogonal sub-space를 explicitly decouple 하고 estimation을 위한 network module을 도입함
- 먼저 input mel-spectrogram은 Range-Space Module (RSM)을 통해 처리됨
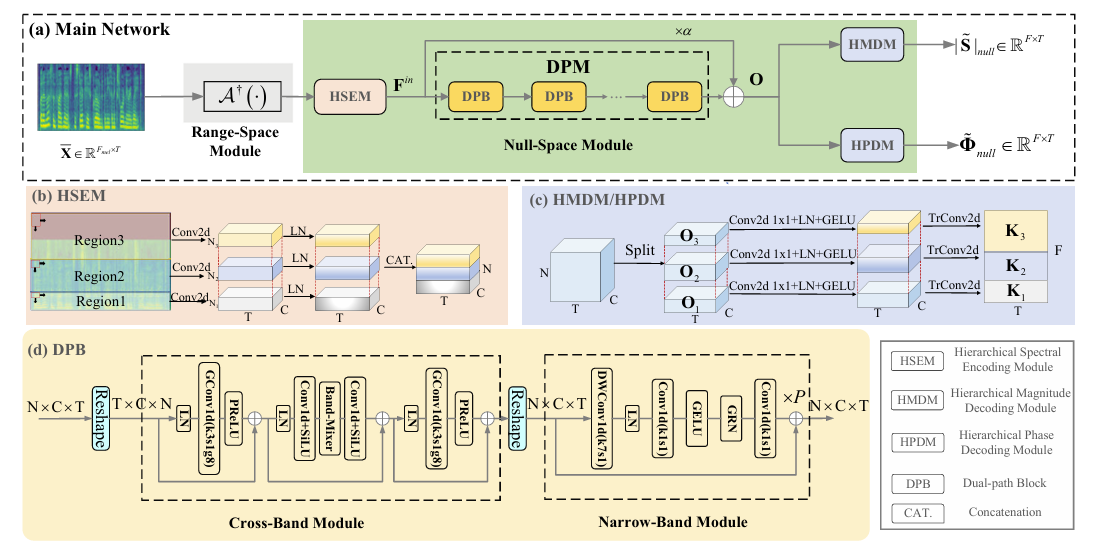
- 이때 mel을 linear-scale domain으로 shift 하기 위해 pseudo-inverse operation을 적용함 - 이후 Hierarchical Spectral Encoding Module (HSEM), Dual-Path Module (DPM), Hierarchical Magnitude/Phase Decoding Module (HMDM/HPDM)으로 구성된 Null-Space Module (NSM)이 적용됨
- 먼저 input mel-spectrogram은 Range-Space Module (RSM)을 통해 처리됨
- Hierarchical Spectral Encoder and Decoder
- HSEM은 input $|\tilde{\mathbf{S}}|_{range}\in\mathbb{R}^{F\times T}$를 $I$ region으로 split 함
- $i$-th spectral region은 $|\tilde{\mathbf{S}}|_{range, i}\in\mathbb{R}^{F_{i}\times T}$와 같음 - 이때 fundamental frequency $F0$와 같은 major acoustic feature는 low/mid frequency region에 존재하므로, 논문은 fine-to-coarse principle을 region division에 적용함
- 즉, region index가 증가함에 따라 $F_{i}$를 gradually increase 함 - 각 spectral region에 대해 spectral compression을 위한 $\text{Conv2d}$와 Layer-Normalization ($\text{LN}$)이 적용됨:
(Eq. 10) $\mathbf{F}_{i}^{in}=\text{LN}\left(\text{Conv2d}\left( |\tilde{\mathbf{S}}|_{range,i}\right)\right)\in\mathbb{R}^{N_{i}\times C\times T}$
- $\mathbf{F}_{i}^{in}$ : $i$-th region의 compressed spectral feature, $\{N_{i},C\}$ : 각각 sub-band, channel size - Decoding 시에는 magnitude, phase estimation을 위해 2개의 branch가 사용됨
- 먼저 input feature $\mathbf{O}\in\mathbb{R}^{N\times C\times T}$를 $I$ region $\{\mathbf{O}_{1},...,\mathbf{O}_{I}\}$로 split 함
- 다음으로 각 region에 separate point-wise $\text{Conv2d}$ layer, $\text{LN}$, $\text{GELU}$ activation을 적용하고, 이후 $\text{TrConv2d}$를 사용하여 spectral target을 recover 함:
(Eq. 11) $\mathbf{K}_{i}=\text{TrConv2d}\left(\text{GELU}\left(\text{LN}\left( \text{Conv2d}1\times1\left( \mathbf{O}_{i}\right)\right)\right)\right)$ - 이후 magnitude branch에서는 non-negativity를 보장하기 위해 $\exp(\cdot)$이 사용되고, phase branch에서는 $\mathbf{K}_{i}$가 real/imaginary component로 split 된 다음 phase calculation을 위해 $\text{Atan2}(\cdot)$이 적용됨
- 해당 방식은 spectrum을 $N$ non-uniform sub-band로 split 하는 기존 band-split strategy과 비교하여 $N$ 보다 적은 $I$ region을 사용하므로 더 빠른 inference가 가능함
- 추가적으로 하나의 spectral region 내에서 network weight가 share 되므로 더 적은 trainable parameter를 요구함
- HSEM은 input $|\tilde{\mathbf{S}}|_{range}\in\mathbb{R}^{F\times T}$를 $I$ region으로 split 함
- Dual-Path Block
- Spectral information modeling을 위해 $B=6$의 Dual-Path Block (DPB)를 stack 함
- 구조적으로는 narrow-/cross-band module로 구성되고, 각각 sub-band/time modeling을 수행함 - 먼저 input feature $\mathbf{F}^{(b)}\in\mathbb{R}^{N\times C\times T}$는 Cross-Band Module (CBM)으로 전달됨
- 이때 CBM은 LN을 적용한 다음, sub-band axis를 따라 kernel 3의 group convolution과 PReLU를 활용하여 neighboring sub-band 간의 correlation을 modeling 함:
(Eq. 12) $\mathbf{F}^{(b)'}=\mathbf{F}^{(b)}+\text{PReLU}\left(\text{GConv1d}\left( \text{LN}\left( \mathbf{F}^{(b)}\right)\right)\right)$ - 다음으로 $\text{Conv1d}$ layer와 $\text{SiLU}$ activation을 사용하여 $C$ 보다 $4\times$ 작은 channel size $C'$으로 squeeze 함
- 이때 global sub-band shuffling을 위해 linear matrix operation으로 instantiate 되는 $\text{BandMixer}$와 channel size recovering을 위한 $\text{Conv1d}, \text{SiLU}$ layer가 추가됨:
(Eq. 13) $\mathbf{F}^{(b)''}=\mathbf{F}^{(b)'}+\text{SiLU}\left(\text{Conv1d}\left( \text{BandMixer}\left(\text{SiLU}\left( \text{Conv1d}\left( \text{LN}\left(\mathbf{F}^{(b)'}\right)\right)\right)\right)\right)\right)$ - 최종적으로 adjacent sub-band 간의 correlation을 반영하기 위해, kernel size 3의 group convolution이 residual connection과 함께 추가적으로 적용됨:
(Eq. 14) $\mathbf{F}^{(b+1)}=\mathbf{F}^{(b)''}+\text{PReLU}\left(\text{GConv1d}\left(\text{LN} \left(\mathbf{F}^{(b)''}\right)\right)\right)$
- 이때 CBM은 LN을 적용한 다음, sub-band axis를 따라 kernel 3의 group convolution과 PReLU를 활용하여 neighboring sub-band 간의 correlation을 modeling 함:
- Narrow-Band Module (NBM)의 경우 Vocos를 따라 adjacent frame 간의 long-term relation을 gradually capture 할 수 있는 $P=2$의 ConvNextv2 block을 stack 함
- 이때 full-band modeling과 달리 모든 sub-band는 network parameter를 share 하고, computational cost를 줄이기 위해 input/hidden layer channel은 $C$로 유지됨
- Spectral information modeling을 위해 $B=6$의 Dual-Path Block (DPB)를 stack 함
- Loss Function
- APNet을 따라 논문은 reconstruction loss, adversarial loss를 training에 사용함
- Reconstruction loss는 log-amplitude loss $\mathcal{L}_{a}$, phase loss $\mathcal{L}_{p}$, real-imaginary loss $\mathcal{L}_{ri}$, mel-loss $\mathcal{L}_{mel}$, consistency loss $\mathcal{L}_{c}$로 구성됨:
(Eq. 15) $\mathcal{L}_{rec}=\lambda_{a}\mathcal{L}_{a}+ \lambda_{p}\mathcal{L}_{p}+\lambda_{ri}\mathcal{L}_{ri}+\lambda_{mel}\mathcal{L}_{mel}+\lambda_{c}\mathcal{L}_{c}$
- $\{\lambda_{a},\lambda_{p},\lambda_{ri},\lambda_{mel},\lambda_{c}\}$ : hyperparameter - 기존 APNet에서는 Instantaneous Phase (IP), Group Delay (GD), Instantaneous Frequency (IF)를 specially-designed sparse matrix를 통해 추출함
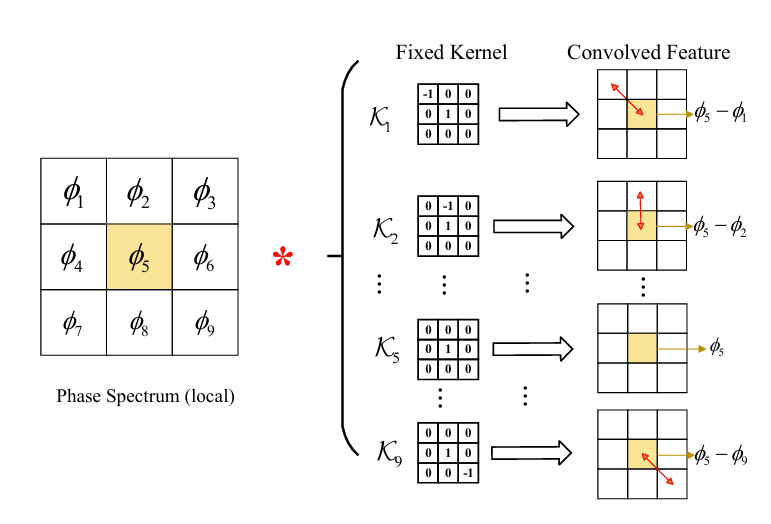
- BUT, 논문에서는 sparse matrix로 인해 해당 computation이 time-consuming 하고 phase differential operation이 2가지 direction만 고려하므로 phase relation을 capture 하는데 한계가 있음 - 이를 해결하기 위해 논문은 Omnidirectional Phase Loss를 도입함
- Adjacent 8 T-F bin의 differential relation을 traverse 하기 위해 fixed parameter를 가진 9개의 $3\times 3$ kernel $\mathcal{K}=\text{Cat}(\mathcal{K}_{1},...,\mathcal{K}_{9})\in\mathbb{R}^{9\times 3\times 3}$을 구성함
- 이때 5-th kernel은 IP를 return 함 - 이를 통해 simple convolution operation 만으로도 phase differential operation을 수행할 수 있음:
(Eq. 16) $ \Delta\Phi=\Phi*\mathcal{K},\,\,\,\Delta\tilde{\Phi}=\tilde{\Phi}*\mathcal{K}$
- $\{\Delta \Phi, \Delta\tilde{\Phi}\}\in \mathbb{R}^{9\times F\times T}$, $*$ : convolution operation - 그러면 anti-wrapping loss를 활용하여 phase loss를 얻을 수 있음
- Adjacent 8 T-F bin의 differential relation을 traverse 하기 위해 fixed parameter를 가진 9개의 $3\times 3$ kernel $\mathcal{K}=\text{Cat}(\mathcal{K}_{1},...,\mathcal{K}_{9})\in\mathbb{R}^{9\times 3\times 3}$을 구성함
- Adversarial loss의 경우 HiFi-GAN의 Multi-Period Discriminator (MPD)와 UnivNet의 Multi-Resolution Spectrogram Discriminator (MRSD)를 사용함
- 이때 hinge GAN loss를 활용하여 얻어지는 discriminator의 adversarial loss는:
(Eq. 17) $\mathcal{L}_{D}=\frac{1}{M}\sum_{m=1}^{M}\max(0,1-D_{m}(\mathbf{s}))+\max(0,1+D_{m}(\tilde{\mathbf{s}}))$
- $D_{m}$ : $m$-th discriminator - Generator의 adversarial loss는:
(Eq. 18) $\mathcal{L}_{g}=\frac{1}{M}\sum_{m=1}^{M}\max(0,1-D_{m}(\tilde{\mathbf{s}}))$ - 추가적으로 Feature Matching loss도 고려할 수 있음:
(Eq. 19) $\mathcal{L}_{fm}=\frac{1}{LM}\sum_{l,m}\left|\mathbf{f}_{l}^{m}(\tilde{\mathbf{s}})- \mathbf{f}_{l}^{m}(\mathbf{s})\right|$
- $\mathbf{f}_{l}^{m}(\cdot)$ : $m$-th sub-discriminator의 $l$-th feature
- 이때 hinge GAN loss를 활용하여 얻어지는 discriminator의 adversarial loss는:
- 결과적으로 얻어지는 final generator loss는:
(Eq. 20) $\mathcal{L}_{G}=\mathcal{L}_{rec}+\lambda_{g}\mathcal{L}_{g}+\lambda_{fm}\mathcal{L}_{fm}$
- $\{\lambda_{g},\lambda_{fm}\}$ : hyperparameter
- Reconstruction loss는 log-amplitude loss $\mathcal{L}_{a}$, phase loss $\mathcal{L}_{p}$, real-imaginary loss $\mathcal{L}_{ri}$, mel-loss $\mathcal{L}_{mel}$, consistency loss $\mathcal{L}_{c}$로 구성됨:
3. Experiments
- Settings
- Dataset : LJSpeech, LibriTTS
- Comparisons : WaveGlow, HiFi-GAN, iSTFTNet, UnivNet, Avocodo, BigVGAN, APNet, FreeV, Vocos
- Results
- 전체적으로 RNDVoC는 우수한 성능을 보임

- LibriTTS에서도 우수한 성능을 달성함

- MUSHRA test 측면에서도 뛰어난 성능을 달성함

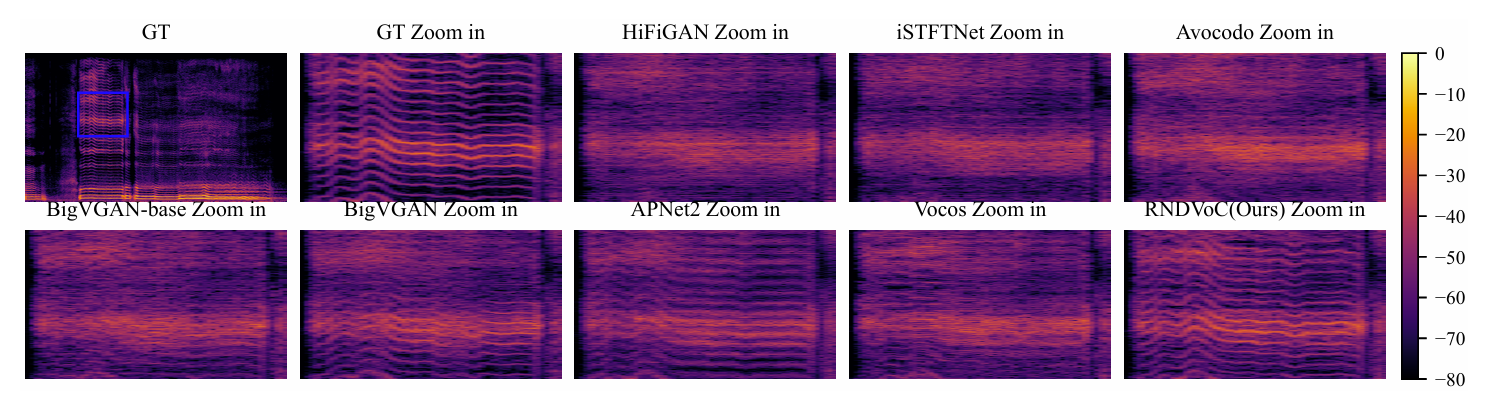
- RNDVoC는 harmonic detail을 효과적으로 recover 할 수 있음
- Ablation Study
- 각 component를 제거하는 경우 성능 저하가 발생함
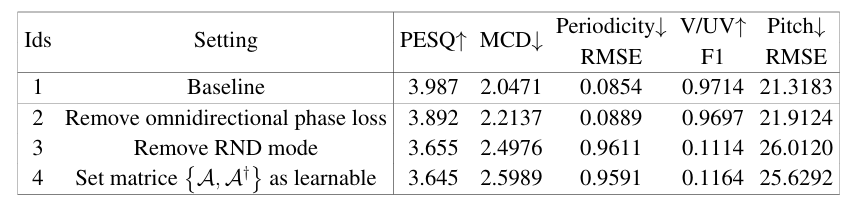
- $\{\mathcal{A}^{\dagger},\mathcal{A}\}$가 fix 되었을 때 range-space와 null-space를 비교해 보면
- Null-space $(\mathbf{I}-\mathcal{A}^{\dagger}\mathcal{A})|\tilde{\mathbf{S}}|_{null}$은 sparse, detailed harmonic structure를 capture 함
- Learnable scenario에서는 null-space estimation이 sparse 하지 않고 orthogonality property가 hold 되지 않음

- Lightweight Design
- RNDVoC-Lite와 RNDVoC-UltraLite는 더 적은 parameter로 HiFi-GAN 보다 나은 성능을 달성함
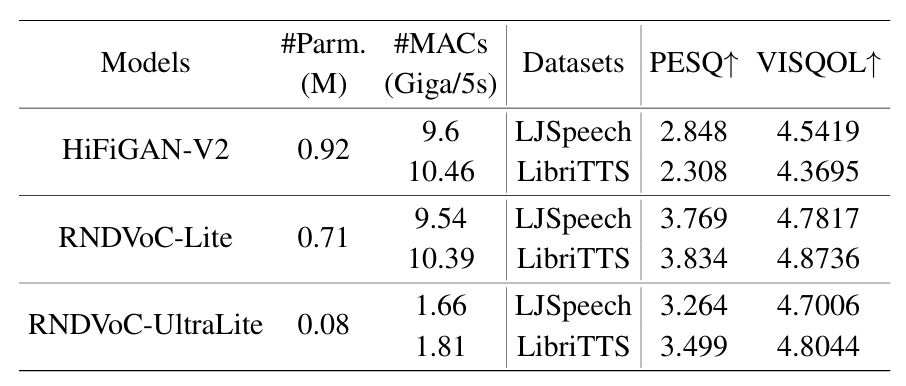
- Spectrogram 측면에서도 lightweight model은 harmonic detail을 효과적으로 반영함
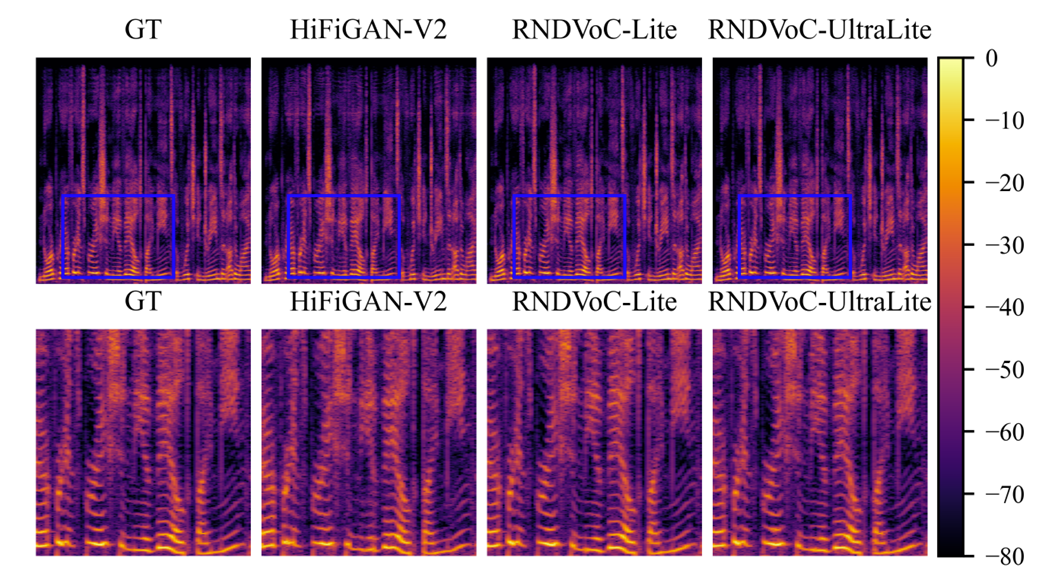
반응형
'Paper > Vocoder' 카테고리의 다른 글
댓글

