[Paper 리뷰] Denoising Diffusion Probabilistic Models

Denoising Diffusion Probabilistic Models

---

• Nonequilibrium thermodynamics에서 영감을 받은 latent variable model인 diffusion probabilistic model을 사용하여 고품질의 이미지 합성을 시도
• Denoising Diffusion Probabilistic Model (DDPM)
  • Diffusion probabilistic model과 Langevin dynamics를 연결하는 denoising score matching을 활용
  • Autoregressive decoding의 generalization으로 해석될 수 있는 progressive lossy decompression을 허용
• 논문 (NeurIPS 2020) : Paper Link

---

1. Introduction

• 다양한 생성 모델이 고품질의 이미지 합성 능력을 보여주고 있음
  • Generative Adversarial Network (GAN), Autoregressive model, Flow, Variational AutoEncoder (VAE)가 대표적
    - 특히 energy-based 모델링과 score matching은 GAN과 비교할만한 합성 품질을 보이고 있음
  • 그중 논문은 diffusion probabilistic model을 활용함
    1. Diffusion model은 finite time 이후에 data와 일치하는 sample을 생성하기 위해, variational inference를 사용하여 학습되는 parameterized Markov chain
    2. 이때 chanin의 transition은 signal이 destory 될 때까지 sampling의 반대 방향으로 data에 점진적으로 noise를 추가하는 diffusion process를 reverse 하는 방식을 학습함
    3. Diffusion이 소량의 Gaussain noise로 구성된 경우, sampling chain transition을 conditional Gaussian으로 설정하여 간단한 neural network parameterization이 가능
  • 위와 같이 diffusion model은 정의하기 쉽지만, 아직까지 고품질 sample을 합성할 수 있다는 보장이 없음
    - 추가적으로 diffusion model의 특정한 parameterization은 여러 noise level에 대한 denoising score matching과 sampling 과정에서의 annealed Langevin dynamics와의 equivalence를 보임

-> 그래서 denoising score matching과 Lagnevin dynamics를 연결하는 Denoising Diffusion Probabilistic Model을 제시

 

• Denoising Diffusion Probabilistic Model (DDPM)
  • Denoising scroe matching과 Lagnevin dynamics를 연결하여 고품질의 이미지 합성 능력을 달성 
  • 특히 DDPM의 lossless codelength는 impreceptible image detail을 설명하는 데 사용되는 것으로 나타남
    
  • Lossy compression을 통해 해당 특성에 대한 정교한 분석을 제시하고 diffusion model의 sampling 과정이 autoregressive decoding과 유사하게 generalize 될 수 있음을 보임

< Overall of DDPM >

• Diffusion probabilistic model과 Langevin dynamics를 연결하는 denoising score matching을 활용
• Autoregressive decoding의 generalization으로 해석될 수 있는 progressive lossy decompression을 허용

2. Background

• Diffusion model은 $p_{\theta }(x_0):=\int p_{\theta }(x_{0:T})\mathrm{d}{x}_{1:T}$ 형식의 latent variable model
  • $x_1,...,x_T$ : data $x_0\sim q(x_0)$와 동일한 dimensionality의 latents
  • Joint 분포 $p_{\theta }(x_{0:T})$는 reverse process라고 하고, $p(x_T)=\mathcal{N}(x_T;0,I)$에서 시작하는 learned Gaussian transition을 가지는 Markov chain으로 정의됨:
    (Eq. 1) $p_{\theta }(x_{0:T}):=p(x_T)\prod _{t=1}^T{p}_{\theta }(x_{t-1}|x_t),p_{\theta }(x_{t-1}|x_t):=\mathcal{N}(x_{t-1};{\mu }_{\theta }(x_t,t),{\mathrm{\Sigma }}_{\theta }(x_t,t))$
  • Diffusion model과 다른 latent variable model 간의 차이점은,
    - Forward/diffusion process라고 하는 근사 posterior $q(x_{1:T}|x_0)$가 variance schedule ${\beta }_1,...,{\beta }_T$에 따라 data에 Gaussian noise를 점진적으로 추가하는 Markov chain으로 fix 된다는 것:
    (Eq. 2) $q(x_{1:T}|x_0):=\prod _{t=1}^{T}q(x_t|x_{t-1}),q(x_t|x_{t-1}):=\mathcal{N}(x_t;\sqrt{1-{\beta }_t}{x}_{t-1},{\beta }_{t}I)$ 
  • Diffusion model의 training은 negative log-likelihood에 대한 variational bound를 최적화하는 것으로 수행됨:
    (Eq. 3) $\mathbb{E}[-\log p_{\theta }(x_0)]\le {\mathbb{E}}_q[-\log \frac{p_{\theta }(x_{0:T})}{q(x_{1:T}|x_0)}]={\mathbb{E}}_q[-\log p(x_T)-\sum _{t\ge 1}\log \frac{p_{\theta }(x_{t-1}|x_t)}{q(x_t|x_{t-1})}]=:L$
    - Forward process variance ${\beta }_t$는 reparameterization을 통해 학습되거나 hyperparameter로 constant 하게 설정되고,
    - Reverse process의 expressiveness는 $p_{\theta }(x_{t-1}|x_t)$에서 Gaussian conditional을 선택함으로써 보장됨
    - 이는 ${\beta }_t$가 작을 때, 두 process 모두 동일한 functional form을 가지기 때문
  • Forward process의 주요한 property는 closed form의 arbitrary timestep $t$에서 $x_t$의 sampling을 허용한다는 것:
    (Eq. 4) $q(x_t|x_0)=\mathcal{N}(x_t;\sqrt{{\overline{\alpha }}_t}{x}_0,(1-{\overline{\alpha }}_t)I)$
    - ${\alpha }_t:=1-{\beta }_t$, ${\overline{\alpha }}_t:=\prod _{s=1}^t{\alpha }_s$
  • 따라서 stochastic gradient descent를 사용하여 $L$의 random term을 최적화함으로써 효율적인 training이 가능함
    - 즉, (Eq. 3)의 $L$을 아래와 같이 rewriting 하면, variance reduction이 가능:
    (Eq. 5) ${\mathbb{E}}_q[\underset{L_T}{\underbrace{D_{KL}(q(x_T|x_0)||p(x_T))}}+\sum _{t>1}\underset{L_{t-1}}{\underbrace{D_{KL}(q(x_{t-1}|x_t,x_0)||p_{\theta }(x_{t-1}|x_t))}}\underset{L_0}{\underbrace{-\log p_{\theta }(x_0|x_1)}}]$
  • (Eq. 5)는 KL-divergence를 사용하여 $p_{\theta }(x_{t-1}|x_t)$를 $x_0$에 대해 condition 할 때 tractable forward process posterior를 통해 직접적으로 비교됨:
    (Eq. 6) $q(x_{t-1}|x_t,x_0)=\mathcal{N}(x_{t-1};{\tilde{\mu }}_t(x_t,x_0),{\tilde{\beta }}_{t}I)$
    (Eq. 7) ${\tilde{\mu }}_t(x_t,x_0):=\frac{\sqrt{{\overline{\alpha }}_{t-1}}{\beta }_t}{1-{\overline{\alpha }}_t}{x}_0+\frac{\sqrt{{\alpha }_t}(1-{\overline{\alpha }}_{t-1})}{1-{\overline{\alpha }}_t}{x}_t,{\tilde{\beta }}_t:=\frac{1-{\overline{\alpha }}_{t-1}}{1-{\overline{\alpha }}_t}{\beta }_t$
    
  • 결과적으로, (Eq. 5)의 모든 KL-divergence는 Gaussian 간의 비교이므로 Monte Carlo 추정 대신, closed form을 사용하여 Rao-Blackwellized 방식으로 계산할 수 있음

3. Diffusion Models and Denoising Autoencoders

• Diffusion model은 latent variable model의 restricted class로 볼 수 있지만, 구현시 많은 자유도를 허용함
  • 따라서 forward process의 variance ${\beta }_t$와 reverse process의 model architecture, Gaussian 분포 parameterization을 choice 해야 함
  • 이러한 choice를 guide 하기 위해, diffusion model에 대한 simplified, weighted variational bound objective와 denoising score matching 간의 explicit 한 연결을 설정
    - 이를 위해 (Eq. 5)의 각 term을 categorize 하여 이를 유도함

Overall of Diffusion Model

- Forward Process and $L_T$

• DDPM은 forward process variance ${\beta }_t$가 reparameterization을 통해 learnable 하다는 점을 무시하고, constant로 fix 함
  • 따라서 근사 posterior $q$에는 learnable parameter가 존재하지 않고 $L_T$는 constant 이므로, training 시 무시 가능함

- Reverse Process and $L_{1:T-1}$

• 이를 기반으로 $1<t\le T$에 대해 $p_{\theta }(x_{t-1}|x_t)=\mathcal{N}(x_{t-1};{\mu }_{\theta }(x_t,t),{\mathrm{\Sigma }}_{\theta }(x_t,t))$에서의 choice를 살펴보면,
  • ${\mathrm{\Sigma }}_{\theta }(x_t,t)={\sigma }_t^{2}I$를 untrained time dependent constant라고 했을 때, ${\sigma }_t^2={\beta }_t$와 ${\sigma }_t^2={\tilde{\beta }}_t=\frac{1-{\overline{\alpha }}_{t-1}}{1-{\overline{\alpha }}_t}{\beta }_t$ 모두 유사한 결과를 보임
    - 이때 첫 번째 choice는 $x_0\sim \mathcal{N}(0,I)$에 optimal 하고 두 번째 choice는 deterministic 한 하나의 point로 설정된 $x_0$에 optimal 함
    - 이는 coordinatewise unit variance가 있는 data에 대한 reverse process entropy의 uppper/lower bound에 해당
  • 따라서 평균 ${\mu }_{\theta }(x_t,t)$를 나타내기 위해 아래의 $L_t$ analysis를 기반으로 specific parameterization을 제안
    1. 먼저 $p_{\theta }(x_{t-1}|x_t)=\mathcal{N}(x_{t-1};{\mu }_{\theta }(x_t,t),{\sigma }_t^{2}I)$에 대해, 다음과 같이 나타낼 수 있음:
       (Eq. 8) $L_{t-1}={\mathbb{E}}_q[\frac{1}{2{\sigma }_t^2}||{\tilde{\mu }}_t(x_t,x_0)-{\mu }_{\theta }(x_t,t)|{|}^2]+C$
       - $C$ : $\theta$에 nondependent 한 constant
       - 여기서 ${\mu }_{\theta }$의 straightforward parameterization은 forward process posterior 평균인 ${\tilde{\mu }}_t$를 예측하는 모델
    2. 이때 (Eq. 4)를 $x_t(x_0,ϵ)=\sqrt{{\overline{\alpha }}_t}{x}_0+\sqrt{1-{\overline{\alpha }}_t}ϵ,ϵ\sim \mathcal{N}(0,I)$로 reparameterization 하고 forward process posterior formula (Eq. 7)을 적용하여 (Eq. 8)을 확장할 수 있음:
       (Eq. 9) $L_{t-1}-C={\mathbb{E}}_{x_0,ϵ}\left[\frac{1}{2{\sigma }_t^2}\left||{\tilde{\mu }}_t(x_t(x_0,ϵ),\frac{1}{\sqrt{{\overline{\alpha }}_t}}(x_t(x_0,ϵ)-\sqrt{1-{\overline{\alpha }}_t}ϵ))-{\mu }_{\theta }(x_t(x_0,ϵ),t)|\right|\right]$
       (Eq. 10) $={\mathbb{E}}_{x_0,ϵ}\left[\frac{1}{2{\sigma }_t^2}{\left||\frac{1}{{\sqrt{\alpha }}_t}(x_t(x_0,ϵ)-\frac{{\beta }_t}{\sqrt{1-{\overline{\alpha }}_t}}ϵ)-{\mu }_{\theta }(x_t(x_0,ϵ),t)|\right|}^2\right]$
       - (Eq. 10)은 ${\mu }_{\theta }$가 주어진 $x_t$에서 $\frac{1}{{\sqrt{\alpha }}_t}(x_t-\frac{{\beta }_t}{\sqrt{1-{\overline{\alpha }}_t}}ϵ)$를 예측해야 하는 것을 나타냄
    3. $x_t$는 model input으로 사용할 수 있으므로, parameterization을 choice 할 수 있음:
       (Eq. 11) ${\mu }_{\theta }(x_t,t)={\tilde{\mu }}_{\theta }(x_t,\frac{1}{\sqrt{{\overline{\alpha }}_t}}(x_t-\sqrt{1-{\overline{\alpha }}_t}{ϵ}_{\theta }(x_t)))=\frac{1}{{\sqrt{\alpha }}_t}(x_t-\frac{{\beta }_t}{\sqrt{1-{\overline{\alpha }}_t}}{ϵ}_{\theta }(x_t,t))$
       - $\theta$ : $x_t$로부터 $ϵ$을 예측하는 function approximator
       - 이때 $x_{t-1}\sim p_{\theta }(x_{t-1}|x_t)$를 sampling 하는 것은, $z\sim \mathcal{N}(0,I)$에서 $x_{t-1}=\frac{1}{{\sqrt{\alpha }}_t}(x_t-\frac{{\beta }_t}{\sqrt{1-{\overline{\alpha }}_t}}{ϵ}_{\theta }(x_t,t))+{\sigma }_{t}z$를 계산하는 것과 같음
  • [Algorithm 2]의 전체 sampling 과정은 data density의 learned gradient로써 ${ϵ}_{\theta }$를 사용하는 Langevin dynamics와 같음
    1. 추가적으로 (Eq. 11)의 reparameterization을 사용하면 (Eq. 10)은 아래와 같이 simplify 됨:
       (Eq. 12) ${\mathbb{E}}_{x_0,ϵ}[\frac{{\beta }_t^2}{2{\sigma }_t^2{\alpha }_t(1-{\overline{\alpha }}_t)}||ϵ-{ϵ}_{\theta }(\sqrt{{\overline{\alpha }}_t}{x}_0+\sqrt{1-{\overline{\alpha }}_t}ϵ,t)|{|}^2]$
    2. 이는 $t$로 index 된 여러 noise scale에 대한 denoising score matching과 유사함
       - 다시 말해, (Eq. 12)는 Langevin-like reverse process (Eq. 11)에 대한 variational bound와 같음
       - 따라서 denoising score matching과 유사한 objective를 최적화하는 것은, Langevin dynamics와 유사한 sampling chain의 finite-time margnial을 fit 하기 위해 variational inference를 사용하는 것과 equivalent 함
  • 요약하자면, reverse process mean function approximator ${\mu }_{\theta }$를 training 하여 ${\tilde{\mu }}_t$를 예측하거나, parameterization을 수정하여 $ϵ$을 예측하도록 training 할 수 있음
    - 이때 $ϵ$-prediction parameterization은 Langevin dynamics와 유사하므로, denoising score matching과 유사한 objective에 대해 diffusion model의 variational bound를 simplify 할 수 있음

Training, Sampling Algorithm

- Data Scaling, Reverse Process Decoder, and $L_0$

• 이미지 data는 $[-1,1]$로 linearly scale 된 $\{0,1,...,255\}$의 interger로 구성된다고 하자
  • 이는 neural network의 reverse process가 standard normal prior $p(x_T)$에서 시작하여 consistently scaled input에서 동작하도록 함
  • Discrete log-likelihood를 얻기 위해, reverse process의 마지막 term을 Gaussian $\mathcal{N}(x_0;{\mu }_{\theta }(x_1,1),{\sigma }_1^{2}I)$에서 파생된 independent discrete decoder로 설정:
    (Eq. 13) $p_{\theta }(x_0|x_1)=\prod _{i=1}^D{\int }_{{\delta }_{-}(x_0^i)}^{{\delta }_{+}(x_0^i)}\mathcal{N}(x;{\mu }_{\theta }^i(x_1,1),{\sigma }_1^2)\mathrm{d}x$
    - ${\delta }_{+}(x)=\{\begin{array}{cc}\mathrm{\infty }& \mathrm{if}x=1\\ x+\frac{1}{255}& \mathrm{if}x<1\end{array}$, ${\delta }_{-}(x)=\{\begin{array}{cc}-\mathrm{\infty }& \text{if}x=-1\\ x-\frac{1}{255}& \text{if}x>-1\end{array}$
    - $D$ : data dimensionality, $i$ : extraction of one coordinate
  • 위 방식은 data에 noise를 추가하거나 scaling의 Jacobian을 log-likelihood에 통합할 필요 없이, variational bound가 discrete data의 lossless codelength 임을 보장함
    - 이는 VAE decoder나 Autoregressive model에서 사용되는 discrete continuous 분포와 유사함
    - 결과적으로 sampling이 끝나면, ${\mu }_{\theta }(x_1,1)$을 noiselessly 하게 나타낼 수 있음

- Simplified Training Objective

• 앞서 정의된 reverse process와 decoder를 사용하면, (Eq. 12)와 (Eq. 13)에서 파생된 term으로 구성된 variational bound는 $\theta$에 대해 differentiable 하므로 trainable 함
  • 이때 아래의 variational bound의 variant를 사용하는 것이 sample 품질에 더 유리하고 더 간단함:
    (Eq. 14) $L_{simple}(\theta ):={\mathbb{E}}_{t,x_0,ϵ}[||ϵ-{ϵ}_{\theta }(\sqrt{{\overline{\alpha }}_t}{x}_0+\sqrt{1-{\overline{\alpha }}_t}ϵ,t)|{|}^2]$
    - $t$는 $[1,T]$ 범위에 대해 uniform 함
    
  • $t=1$인 경우, ${\sigma }_1^2$과 edge effect를 무시하고 Gaussian probability density function과 bin width의 곱으로 근사된 discrete decoder (Eq. 13)의 적분을 가지는 $L_0$에 해당함
  • $t>1$인 경우, NCSN denoising score matching model에서 사용하는 loss weighting과 유사한 (Eq. 12)의 unweighted version에 해당함
    - Forward process variance ${\beta }_t$가 fix 되어 있으므로 $L_T$는 나타나지 않음
    - 결과적으로 [Algorithm 1]은 이러한 simplified objective를 사용하여 training을 수행함
• Simplified objective (Eq. 14)는 (Eq. 12)의 weight를 제거하므로 standard variational bound와 비교하여 reconstruction의 다양성을 증가시킬 수 있음
  • 특히 diffusion process 설정은 작은 $t$에 해당하는 down-weight loss term에 대한 simplified objective를 제공
    
  • 이러한 term은 아주 적은 양의 noise로 data를 denoising 하도록 network를 학습시키므로, network가 더 큰 $t$ term에서 더 어려운 denoising 작업에 집중할 수 있도록 down-weight 하는 것이 좋음
    
  • 결과적으로 이러한 reweighting을 통해 DDPM은 더 우수한 sample 품질을 얻을 수 있음

4. Experiments

- Settings

• Dataset : CIFAR10, LSUN, CelebA-HQ
• Comparisons : EBM, JEM, BigGAN, StyleGAN, Gated PixelCNN, Sparse Transformer, PixelIQN, NCSN, SNGAN

- Results

• Sample Quality
  • CIFAR10에 대한 Inception score, FID, negative log-likelihood (lossless codelength)를 비교해 보면
  • DDPM이 가장 우수한 성능을 보이는 것으로 나타남

합성 품질 비교

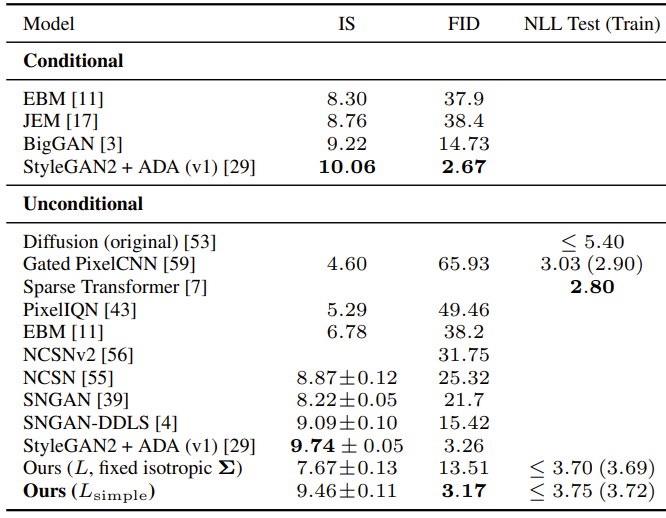
• 특히 simple objective $L_{simple}$을 사용한 DDPM은 true variational bound에 대해 더 나은 codelength를 생성하고 더 우수한 합성 품질을 달성함

CelebA-HQ, CIFAR10에 대한 DDPM 합성 sample

LSUN에 대한 DDPM 합성 Sample

• Reverse Process Parameterization and Training Objective Ablation
  • $\tilde{\mu }$의 예측은 (Eq. 14)의 unweighted mean squared error 대신 true variational bound에 대해 학습될 때만 잘 작동함
  • Reverse variance를 학습하면 fixed variance에 비해 학습이 unstable 하고 품질이 저하되는 것으로 나타남
  • 따라서 논문에서 제안한 바와 같이, fixed variance와 simplified objective를 사용하면 더 우수한 성능을 얻을 수 있음

Reverse Process Parameterization과 Training Objective Ablation 결과

• Progressive Coding
  • DDPM의 lossless codelength는 energy-based model과 annealed importance를 사용하는 score matching 방법들 보다는 좋은 결과를 보이지만, 다른 likelihood-based model 보다는 경쟁력이 떨어짐
    - 그럼에도 불구하고 DDPM은 우수한 합성 품질을 보이기 때문에, diffusion model에는 lossy compressor를 만드는 inductive bias가 존재한다고 볼 수 있음
  • Variational bound term $L_1+...+L_T$를 rate로 $L_0$를 distortion으로 처리하면, DDPM은 CIFAR10에 대해 1.78 bits/dim을 보임
    - 이는 0에서 255까지의 범위에서 0.95의 mean squared error에 해당함
    - 다시 말해, lossless codelength의 절반 이상은 imperceptible distortion을 나타냄

Total Expected Codelength의 계산 과정

• Progressive Lossy Compression
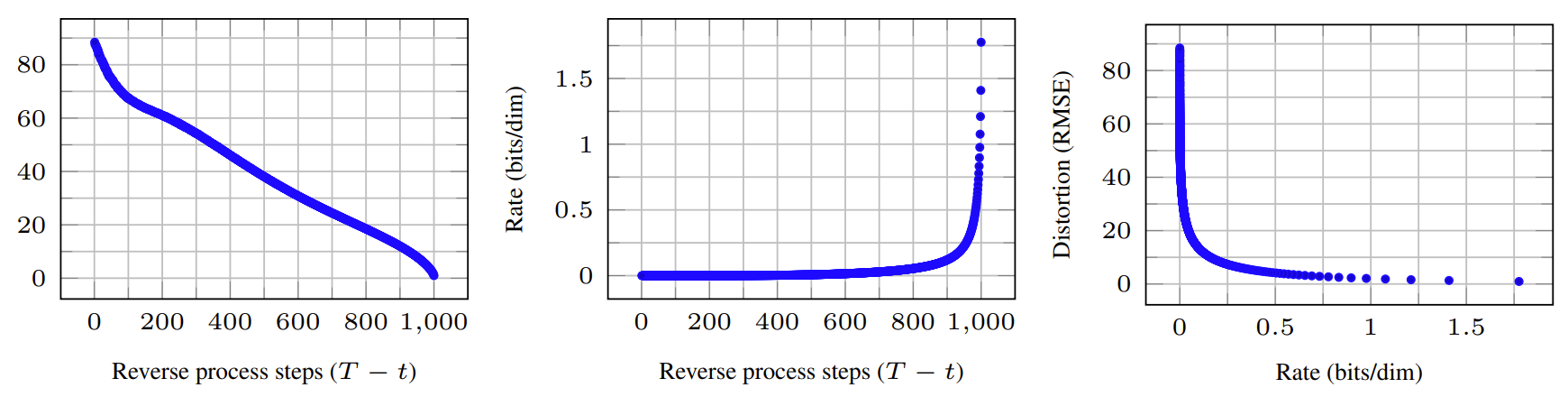
  • (Eq. 5)를 반영하는 progressive lossy code를 DDPM에 도입하여 rate-distortion behavior를 조사
  • 이때 receiver는 모든 $t$에서 partial information $x_t$를 가지고 아래와 같이 점진적으로 추정할 수 있음:
    (Eq. 15) $x_0\approx {\hat{x}}_0=(x_t-\sqrt{1-{\overline{\alpha }}_t}{ϵ}_{\theta }(x_t))/\sqrt{{\overline{\alpha }}_t}$
  • 결과적으로 CIFAR10에 대한 rate-distortion plot을 확인해 보면, distortion은 low-rate region에서 급격하게 감소하는 것으로 나타남
    - 이는 대부분의 bit가 imperceptible distortion에 할당되었다는 것을 의미 

Rate-Distortion Plot

• Progressive Generation
  • Random bit의 progressive decompression을 통한 unconditional generation process를 실험해 보면
  • Large scale의 이미지 feature가 가장 먼저 나타나고 detailed feature는 나중에 나타남

CIFAR10에 대한 Progressive Generation 결과

• $t$에 대해 $x_t$를 frozen 했을 때 $x_0\sim p_{\theta }(x_0|x_t)$의 결과를 확인해 보면,
  • $t$가 작으면 fine detail을 제외한 나머지 모든 detail이 preserve 되고, $t$가 크면 large sacel feature만 preserve 됨
  • 이는 conceptual compression으로도 볼 수 있음

$t$별 sampling의 차이 비교

• Connection to Autoregressive Decoding
  • (Eq. 5)의 variational bound는 다음과 같이 rewritten 할 수 있음:
    (Eq. 16) $L=D_{KL}(q(x_T)||p(x_T))+{\mathbb{E}}_q[\sum _{t\ge 1}{D}_{KL}(q(x_{t-1}|x_t)||p_{\theta }(x_{t-1}|x_t))]+H(x_0)$
    - $q(x_t|x_{t-1})$이 $t$-th coordinate를 mask 하도록 하고, blank 이미지에 모든 mass를 place 하도록 $p(x_T)$를 설정하고, $p_{\theta }(x_{t-1}|x_t)$를 취해 fully expressive conditional 분포로 표현할 수 있음
  • 따라서 Gaussian diffusion model (Eq. 2)를 data coordinate의 reordering으로 표현할 수 없는, generalized bit ordering을 가진 autoregressive model로써 interpret 할 수 있음
    - 이러한 reordering은 sample 품질에 영향을 주는 inductive bias를 제공하므로, DDPM의 Gaussian diffusion도 마찬가지로 유사한 목적을 가짐
• Interpolation
  • $q$를 stochastic encoder로 사용하여 latent space에서 source image $x_0,x_0^{\prime }\sim q(x_0)$를 interpolate 할 수 있음
  • 결과적으로 reverse process를 통해 고품질의 reconstruction과 pose, skin tone, hairstyle, background 등을 부드럽게 변화시키는 plausible interpolation이 생성됨
    - 다만 eyewear의 경우 이러한 interpolation이 나타나지 않음
    - 추가적으로 $t$가 클수록 더 coarse 하고 다양한 interpolation이 나타남

Interpolation 결과