티스토리 뷰
Paper/Vocoder
[Paper 리뷰] SpecGrad: Diffusion Probabilistic Model based Neural Vocoder with Adaptive Noise Spectral Shaping
feVeRin 2024. 1. 16. 15:38반응형
SpecGrad: Diffusion Probabilistic Model based Neural Vocoder with Adaptive Noise Spectral Shaping
- Denoising Diffusion Probabilistic Model을 사용하는 neural vocoder는 주어진 acoustic feature에 대한 diffusion noise 분포를 조절함
- SpecGrad
- Time-varying spectral envelope가 conditioning log mel-spectrogram에 가까워지도록 diffusion noise를 조절하는 neural vocoder
- Time-varying filter를 통한 high-frequency band에서의 품질 상승
- 논문 (INTERSPEECH 2022) : Paper Link
1. Introduction
- Neural vocoder는 acoustic feature가 주어졌을 때, 그에 맞는 speech waveform을 생성하는 것을 목표로 함
- 특히 vocoder는 Text-to-Speech (TTS), Speech Enhancement의 필수 요소로써 낮은 계산 비용으로 high-fidelity의 waveform을 합성하는 것이 중요함
- Denoising Diffusion Probabilistic Model (DDPM)은 높은 합성 품질과 제어 가능한 계산 비용으로 주목을 받고 있음
- DDPM은 denoising process로 random signal을 speech waveform으로 반복적으로 변환하는 방식을 활용
- BUT, DDPM은 high-fidelity의 waveform을 얻으려면 많은 반복을 필요로 함
-> 따라서, 합성 품질을 유지하면서 반복 수를 줄이기 위해 noise schedule을 주로 활용
- PriorGrad는 acoustic model의 prior 분포를 활용하여 DDPM vocoder를 개선
- Conditioning log mel-spectrogram을 기반으로 diffusion noise를 조절하는 방식
- 이때 diffusion 분포는 대각 성분이 mel-spectrogram의 frame-wise energy인 대각 공분산 matrix를 사용하는 Gaussian 분포 - 해당 분포는 대각 공분산 matrix가 time-domain에서 waveform의 power를 나타내므로,
- 결과적으로 각 sample point에 대한 noise schedule의 scaling으로 고려할 수 있음
- Conditioning log mel-spectrogram을 기반으로 diffusion noise를 조절하는 방식
-> 그래서 conditioning log mel-spectrogram에 diffusion noise의 spectral envelope를 적합하는 SpecGrad를 제안
- SpecGrad
- DDPM의 diffusion noise 생성과 cost function에서 사용되는 decomposed 공분산 matrix로부터,
- Time-Frequency (T-F) domain에서 time-varying filtering을 적용
- 이를 통해 diffusion noise의 spectral envelope에 대한 공분산 matrix를 설계
< Overall of SpecGrad >
- Spectral envelope가 conditioning log mel-spectrogram에 가까워지도록 diffusion noise를 조절하는 neural vocoder
- Time-varying filter를 도입하여 spectral envelope의 공분산 matrix를 설계
- 결과적으로 기존 DDPM 기반 neural vocoder 보다 우수한 합성 품질을 달성

2. Conventional Methods
- DDPM-based Neural Vocoder
- $D$-point speech waveform $x_{0} \in \mathbb{R}^{D}$가 conditioning log mel-spectrogram $c = (c_{1}, ..., c_{K}) \in \mathbb{R}^{FK}$로부터 생성된다고 하자
- 이때 $c_{k} \in \mathbb{R}^{F}$는 $k$-th time에 대한 $F$-point log mel-spectrogram이고, $K$는 time frame의 수
- 이때 $x_{0}$를 $q(x_{0}|c)$로 나타내는 확률 밀도 함수(PDF)를 찾는 것을 목표로 함 - 따라서, DDPM-based neural vocoder는 $q(x_{T}) = \mathcal{N}(0,I)$에서 시작하여 learned Gaussian transition을 가지는 $x_{t} \in \mathbb{R}^{D}$ Markov chain을 활용하는 latent variable model:
(Eq. 1) $q(x_{0}|c)=\int_{\mathbb{R}^{DT}} q(x_{T})\prod_{t=1}^{T}q(x_{t-1}|x_{t},c)d{x_{1}} \dotsb dx_{T}$
- 이때, $q(x_{t-1} | x_{t},c)$를 모델링하기 위해서, $x_{0}$는 $x_{T}$에서 $x_{t}$로부터 $x_{t-1}$의 recursive sampling을 통해 얻어짐
- 이때 $c_{k} \in \mathbb{R}^{F}$는 $k$-th time에 대한 $F$-point log mel-spectrogram이고, $K$는 time frame의 수
- DDPM에서 $x_{t-1}$은 $p(x_{t}|x_{t-1}) = \mathcal{N} ( \sqrt{1-\beta_{t}}x_{t-1}, \beta_{t}I )$에 의해 주어지는 noise schedule $\{ \beta_{1}, ..., \beta_{T} \}$에 따라 Gaussian noise를 점진적으로 추가하는 diffusion process에 의해 생성됨
- 이때, 임의의 time step $t$에서 $x_{t}$를 아래 식을 통해 closed form으로 sampling 가능:
(Eq. 2) $x_{t} = \sqrt{\bar{\alpha}_{t}}x_{0} + \sqrt{1-\bar{\alpha_{t}}}\epsilon$
- $\alpha_{t} = 1 - \beta_{t}$, $\bar{\alpha}_{t} = \prod_{s=1}^{t} \alpha_{s}$, $\epsilon \sim \mathcal{N}(0,I)$ - 여기서 DDPM-based neural vocoder는 $x_{t}$에서 $\epsilon$을 $\epsilon = \mathcal{F}_{\theta} (x_{t}, c, \beta_{t})$로 예측하는 parameter $\theta$를 가지는 Deep Neural Network (DNN) $\mathcal{F}$를 사용
- 만약 $\beta_{t}$가 충분히 작다면, $q(x_{t-1}|x_{t},c)$는 $\mathcal{N}(\mu_{t}, \gamma_{t}I)$로 주어지고, 이때 $\mu_{t}$는:
(Eq. 3) $\mu_{t} = \frac{1}{\sqrt{\alpha_{t}}} \left( x_{t} - \frac{1-\alpha_{t}}{\sqrt{1-\bar{\alpha_{t}}}} \mathcal{F}_{\theta} (x_{t}, c, \beta_{t}) \right) $
- $\gamma_{t} = \frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_{t}}\beta_{t}$ - 이후 DNN $\mathcal{F}$는 Evidence Lower BOund (ELBO)를 최대화함으로써 학습될 수 있지만, 대부분의 DDPM-neural vocoder는 단순화된 loss를 사용함
- 대표적으로 WaveGrad는 $\ell_{1}$ norm을 사용:
(Eq. 4) $\mathcal{L}^{WG} = || \epsilon-\mathcal{F}_{\theta}(x_{t},c,\beta_{t})||_{1}$
- $|| \cdot ||_{p}$ : $\ell_{p}$ norm
- 이때, 임의의 time step $t$에서 $x_{t}$를 아래 식을 통해 closed form으로 sampling 가능:
- PriorGrad
- PriorGrad는 adaptive prior $\mathcal{N}(0, \Sigma)$를 도입한 DDPM-based neural vocoder
- 이때 $\Sigma$는 conditioning log mel-spectrogram $c$로부터 계산됨
- PriorGrad의 특징
- 모든 diffusion step에 대해서 $\epsilon$은 $\mathcal {N}(0, I)$로부터 sampling 됨
- $\Sigma$에 따른 Mahalanobis distance를 loss로 사용:
(Eq. 5) $\mathcal{L}^{PG} = (\epsilon - \mathcal{F}_{\theta} (x_{t}, c, \beta_{t}))^{T}\Sigma^{-1}(\epsilon - \mathcal{F}_{\theta}(x_{t}, c, \beta_{t}))$
- $^{T}$ : transpose
- PriorGrad에서 공분산 matrix는 $\Sigma = diag [ ( \sigma_{1}^{2}, \sigma_{2}^{2}, ..., \sigma_{D}^{2})]$으로 나타냄
- $\sigma_{d}^{2}$ : $c_{k}$의 normalized frame-wise energy를 interpolating 하여 계산된 $d$-th sample의 signal power
- $diag$ : 대각 성분이 input vector인 diagonal matrix
3. Proposed Method
- SpecGrad
- PriorGrad의 성능은 공분산 matrix $\Sigma$에 의해 결정됨
- 특히 PriorGrad의 ELBO는 $\Sigma$가 $x_{0}$의 공분산에 가까울수록 작아짐
- 이러한 $\Sigma$를 얻기 위해서는 amplitude spectrum $\epsilon$을 $x_{0}$와 유사하게 만들어야 함
- 따라서, SpecGrad는 spectral envelope를 $\Sigma$에 통합하는 방식을 제안함
- $\Sigma$는 positive semi-definite이므로, $\Sigma = LL^{T}$로 decompose 될 수 있음
- $\mathcal{N}(0,\Sigma)$에서 sampling은 $\tilde{\epsilon} \sim \mathcal{N}(0,I)$와 (Eq. 5)에 따라 $\epsilon = L\tilde{\epsilon}$으로 표현할 수 있고, 이를 다시 쓰면:
(Eq. 6) $\mathcal{L}^{SG} = || L^{-1}(\epsilon - \mathcal{F}_{\theta} (x_{t}, c,\beta_{t})) ||_{2}^{2}$ - 이때 SpecGrad는 낮은 계산 비용으로 high-fidelity의 waveform을 생성하는 $L \in \mathbb{R}^{D \times D}$을 설계하는 것을 목표로 함
- $L$에 대해서 요구되는 property는:
- $\epsilon \,\, (=L\tilde{\epsilon})$의 amplitude spectrum은 $x_{0}$에 근사해야 함
- ELBO를 최소화하는데 필수적이기 때문 - $L$과 $L^{-1}$간의 곱은 계산 효율적이어야 함
- $L$과 $L^{-1}$이 학습과정에서 반복적으로 사용되고, 첫 번째 property로 인해 training sample $x_{0}$에 의존적이기 때문
- $\epsilon \,\, (=L\tilde{\epsilon})$의 amplitude spectrum은 $x_{0}$에 근사해야 함
- $\mathcal{N}(0,\Sigma)$에서 sampling은 $\tilde{\epsilon} \sim \mathcal{N}(0,I)$와 (Eq. 5)에 따라 $\epsilon = L\tilde{\epsilon}$으로 표현할 수 있고, 이를 다시 쓰면:
- 위의 요구사항을 만족하기 위해, SpecGrad는 T-F domain에 time-varying filter를 적용함
- Window size $N$을 가지는 STFT를 $NK \times D$의 matrix $G$로 표현할 때, T-F domain에서의 time-varying filter는:
(Eq. 7) $L = G^{+}MG$
- $M = diag [(m_{1,1}, ..., m_{N,K})] \in \mathbb{C}^{NK \times NK}$ : filter $m_{n,k}$를 정의하는 diagonal matrix
- $m_{n,k} \neq 0$ : $(n,k)$-th T-F bin에 곱해지는 coefficient
- $G^{+}$ : dual window를 적용한 inverse STFT의 matrix representation - 이를 통해 $L$ design 문제를 filter design 문제로 recast 할 수 있음
- 따라서 $\epsilon \,\, (=L\tilde{\epsilon})$이 $x_{0}$의 spectral envelope에 근사하도록 $M$을 설계
- 이때, $L^{-1}$을 $L^{-1} \approx G^{+} M^{-1}G$로 근사 - $M$과 $M^{-1}$이 diagonal 하므로, $L$과 근사된 $L^{-1}$은 FFT를 사용하여 $O(KN \, log \, N)$ 내에 연산될 수 있음
- 이때 $K$개의 FFT를 병렬로 계산할 수 있으므로, (Eq. 7)에 대한 계산 비용은 완화될 수 있음
- Window size $N$을 가지는 STFT를 $NK \times D$의 matrix $G$로 표현할 때, T-F domain에서의 time-varying filter는:
- Implementation
- SpecGrad는 아래의 [Alogrithm 1]과 [Algorithm 2]에 따라 학습/추론됨
- 이때 DDPM neural vocoder와 PriorGrad의 차이는, diffusion noise sampling $G^{+}MG\tilde{\epsilon}$과 loss function (Eq. 6) 뿐 임
- 따라서 SpecGrad는 noise schedule를 활용할 수 있고, 결과적으로 SpecGrad는 WaveGrad의 추론 속도는 거의 동일함 - SpecGrad는 T-F domain filter $M$을 계산하기 위해, cepstrum을 통해 spectral envelope를 추정함
- 대응하는 power spectrogram을 계산하기 위해 mel-compression matrix에 대한 pseudo-inverse를 conditioning log mel-spcetrogram $c$에 적용
- $r$-th order lifter를 적용하여 각 time frame에 대한 spectral envelope를 계산
- 이때 학습과정에서 numerical stability를 위해 0.01을 추정된 envelope에 더함 - $k$-th time frame에 대한 coefficient $m_{1,k}, ..., m_{N,k}$는 얻어진 envelope에 대한 minimum phase response로 계산
- Filter $M$을 구성하기 위해서 다른 방법을 사용할 수도 있음
- 다만 spectrogram을 직접 사용하는 것보다 제안된 envelope 추정을 활용하는 것이 더 만족스러운 결과를 제공함
- 이때 DDPM neural vocoder와 PriorGrad의 차이는, diffusion noise sampling $G^{+}MG\tilde{\epsilon}$과 loss function (Eq. 6) 뿐 임


3. Experiments
- Settings
- Dataset : Internal speech dataset
- Comparisons : WaveGrad, PriorGrad
- Inference Noise Schedule : 아래 표 참조

- Results
- SpecGrad는 주관적/객관적 성능 평가에서 모두 WaveGrad, PriorGrad 보다 우수한 성능을 보임
- 특히 noise schedule 선택에 관계없이 SpecGrad의 성능이 가장 우수함


- Side-by-Side test를 수행했을 때도 마찬가지로, SpecGrad의 성능이 WaveGrad, PriorGrad보다 우수한 것으로 나타남
- SpecGrad는 conditioning log mel-spectrogram에 따라 high-frequecny component를 줄일 수 있기 때문
- 결과적으로 frequency가 높아질수록 추정된 noise를 제거하는 양이 적어지기 때문에 artifact 방지가 가능

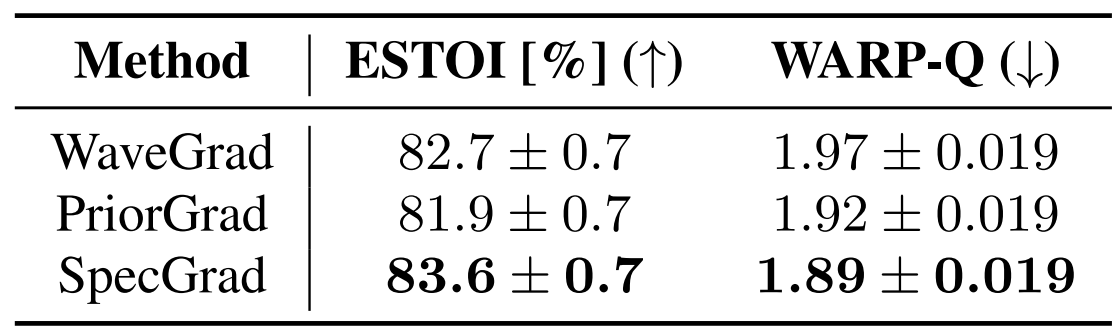
- Evaluation as Speech Enhancement Backend
- SpecGrad에 대한 robustness를 알아보기 위해, DDPM-based Vocoder를 speech enhancement의 backend로 사용
- 결과적으로, SpecGrad의 성능이 WaveGrad, PriorGrad보다 우수하게 나타남
반응형
'Paper > Vocoder' 카테고리의 다른 글
댓글

