[Paper 리뷰] PeriodWave: Multi-Period Flow Matching for High-Fidelity Waveform Generation

PeriodWave: Multi-Period Flow Matching for High-Fidelity Waveform Generation

---

• High-resolution waveform signal의 natural periodic feature를 explicitly disentangle 할 수 있는 generator가 필요함
• PeriodWave
  • Vector field를 추정할 때 waveform signal의 periodic feature를 capture 하는 period-aware flow matching estimator를 도입
  • Waveform signal의 periodic feature를 capture 하는 multi-period estimator를 활용
  • 추가적으로 waveform generation에서 high-frequency noise를 reduce 할 수 있는 FreeU를 도입
• 논문 (ICLR 2025) : Paper Link

---

1. Introduction

• Neural vocoder는 mel-spectrogram/linguistic representation과 같은 low-resolution acoustic representation을 high-resolution waveform으로 변환함
  • 특히 Universal vocoder는 일반적인 acoustic feature인 mel-spectrogram 외에도 SoundStream, DAC 등과 같은 highly compressed representation에서 high-fidelity waveform을 생성하는 것을 목표로 함
    - 그 외에도 unseen voice, instruments, dynamic environment와 같은 Out-Of-Distribution (OOD) scenario에 대해서도 generalize 되어야 함
  • 기존의 Generative Adversarial Network (GAN)-based model은 waveform signal의 different character를 capture 하는 discriminator를 도입하여 waveform generation을 수행함
    1. 대표적으로 MelGAN은 multi-scale discriminator, HiFi-GAN은 multi-period discriminator, UnivNet은 multi-resolution spectrogram discriminator을 도입함
    2. 그 외에도 BigVGAN은 OOD modeling을 위해 snake activation을 활용하고, Vocos는 time-axis representation에 대한 upsampling 의존성을 줄여 efficiency를 향상함
  • BUT, 해당 GAN-based model은 high-fiedlity waveform 생성에서 다음의 한계점을 가짐:
    1. Audio quality를 향상하기 위해서는 많은 discriminator가 필요하므로 training time이 증가함 
    2. Multiple loss term 간의 balancing을 위한 hyper-parameter tuning이 필요함 
    3. Train-inference mismatch scenario에서는 metallic sound나 hissing noise가 발생할 수 있음 
  • 한편으로 high-resolution waveform modeling을 위해 diffusion을 활용할 수도 있음
    1. DiffWave, WaveGrad와 같은 기존의 diffusion-based modeling은 high-frequency information modeling이 어렵고 high-fidelity waveform을 얻기 위해서는 많은 iterative step이 필요함
    2. 특히 PriorGrad, FastDiff의 data-driven prior나 noise schedule predictor를 통해 iteration step 문제는 개선할 수 있음
       - BUT, 여전히 high-frequency modeling은 한계가 존재함

-> 그래서 high-resolution waveform signal의 natural periodic feature를 반영할 수 있는 PeriodWave를 제안

 

• PeriodWave
  • Optimal transport path를 통해 vector field를 추정하는 Conditional Flow Matching을 채택
  • 추가적으로 overlap을 회피하기 위해 prime number 기반의 Multi-Period Estimator를 활용하고 inference speed 향상을 위해 period-wise batch inference와 period-conditional universal estimator를 적용
  • High-frequency information modeling의 경우, Discrete Wavelet Transformation (DWT)와 FreeU를 도입

< Overall of PeriodWave >

• 다양한 implicit periodic representation을 반영할 수 있는 waveform generation model
• 결과적으로 기존보다 뛰어난 합성 품질을 달성

2. Method

• Flow matching model은 Continuous Normalizing Flow (CNF)에 대한 swift, simulation-free training이 가능하고 readily incorporable 한 Optimal Transport (OT) trajectory를 제공함
  - 따라서 논문은 waveform distribution에서 complex transformation을 manage 하기 위해 flow matching model을 도입함

PeriodWave Architecture

- Preliminary: Flow Matching with Optimal Transport Path

• Data space $\mathbb{R}^{d}$의 unknown distribution $q(x)$로부터 sampling 된 observation $x\in\mathbb{R}^{d}$가 있다고 하자
  • 그러면 CNF는 time-dependent vector field $v_{t}$를 사용하여 simple prior $p_{0}$를 target distribution $p_{1}\approx q$로 transform 함
  • 여기서 flow $\phi_{t}$는 다음의 Ordinary Differential Equation (ODE)로 정의됨:
    (Eq. 1) $\frac{d}{dt}\phi_{t}(x)=v_{t}(\phi_{t}(x);\theta),\,\,\,\phi_{0}(x)=x,\,\,\,x\sim p_{0}$
    
  • Flow matching objective는 vector field $v_{t}(x)$를 desired probability path $p_{t}$를 생성하는 ideal vector field $u_{t}(x)$에 match 하는 것을 목표로 함
    
    1. 결과적으로 flow matching objective는 loss function $\mathcal{L}_{FM}(\theta)$를 minimize 하는 것을 포함함
    2. 즉, model의 vector field $v_{\theta}(t,x)$를 target vector field $u_{t}(x)$로 regress 하는 것과 같음:
       (Eq. 2) $\mathcal{L}_{FM}(\theta)=\mathbb{E}_{t\sim[0,1],x\sim p_{t}(x)}||v_{\theta}(t,x)-u_{t}(x)||_{2}^{2}$
    3. 이때 $u_{t},p_{t}$에 access 하는 것은 impractical 하므로 Conditional Flow Matching (CFM)을 사용함:
       (Eq. 3) $\mathcal{L}_{CFM}(\theta)=\mathbb{E}_{t\sim[0,1],x\sim p_{t}(x|z)}||v_{\theta}(t,x)-u_{t}(x|z)||_{2}^{2}$
    4. Noise condition $x_{0}\sim\mathcal{N}(0,1)$로 generalize 하면, OT-CFM loss는:
       (Eq. 4) $\mathcal{L}_{OT\text{-}CFM}(\theta)=\mathbb{E}_{t,q(x_{1}),p_{0}(x_{0})}||u_{t}^{OT}(\phi_{t}^{OT}(x_{0})|x_{1})-v_{t}(\phi_{t}^{OT}(x_{0})|\mu;\theta)||^{2}$
       - $\phi_{t}^{OT}(x_{0})=(1-(1-\sigma_{\min})t)x_{0}+tx_{1}$
       - $u_{t}^{OT}(\phi_{t}^{OT}(x_{0})|x_{1})=x_{1}-(1-\sigma_{\min})x_{0}$
  • 해당 approach를 통해 data transformation을 efficiently manage 하고 optimal transport path를 integrate 하여 training speed, efficiency를 향상할 수 있음

CFM, ODE Solver를 통한 Waveform Generation

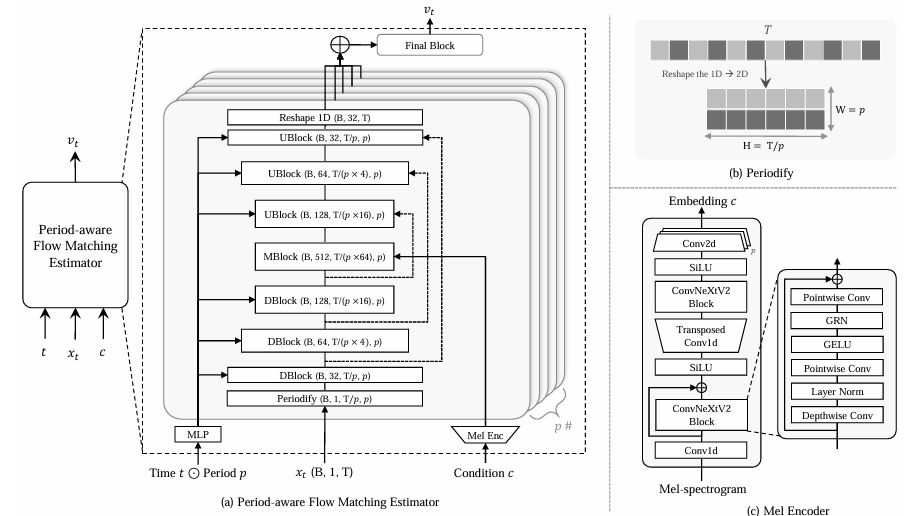
- Period-Aware Flow Matching Estimator

• High-quality waveform generation을 위한 vector field estimating 시 different periodic feature를 reflect 할 수 있는 Period-Aware Flow Matching Estimator를 도입함
  • 먼저, time-specific vector field estimation을 위해 time-conditional UNet-based structure를 사용함
    - 특히 기존의 UNet-based decoder와 달리 서로 다른 period를 가지는 reshaped input signal의 mixture를 사용함
    - 이때 HiFi-GAN과 유사하게 length $T$의 $p_{t}(x)$에서 sampling 된 1D data를 height $T/p$, width $p$로 reshape 하는 Periodify process를 적용함
  • 이후 single estimator에서 period-aware feature extraction을 위해 reshaped sample의 specific period를 indicate 하도록 period embedding을 condition 함
    1. Input signal에서 overlap을 방지하고 different periodic feature를 capture 하기 위해 $[1,2,3,5,7]$의 period를 사용
    2. 구조적으로는 down/upsampling layer와 ResNet block의 2D convolution을 채택하고, $3$의 kernel size와 각 UNet block에 대한 dilation은 $1,2$를 사용함
       - 여기서 각 signal을 $[4,4,4]$로 downsampling 하여 middle block representation이 height $T/(p\times 64)$, width $p$를 가지도록 함
  • 각 period의 representation을 추출한 다음, 2D representation을 각 period path에 대한 1D signal의 original shape로 reshape 하고 모든 period path의 representation을 summation 함
    - Final block은 period representation mixture에서 vector field를 추정함
  • Mel-spectrogram conditional generation의 경우, mel-spectrogram에서 추출한 conditional representation만 각 period path의 UNet middle layer representation에 add 함
    1. 구조적으로는 time-frequency modeling을 위한 conditional information을 추출하기 위해, ConvNeXt-V2-based Mel encoder를 도입함
    2. 특히 논문은 기존 Vocos에서 채택된 ConvNeXt 대신 ConvNeXt-V2 block을 활용하여 Mel encoder를 구성하고, 해당 block output을 Period-Aware Flow Matching Estimator에 전달함
       - 여기서 $256$ hop size를 사용하므로 mel-spectrogram length는 $T/256$이 됨
       - Conditional representation을 align 하기 위해 $4\times$ upsampling 하고 $[1,2,3,5,7]$ period로 downsampling 하여 $T/(p\times 64)$의 shape를 얻음
  • 추가적으로 inference speed를 향상하기 위해 다음의 방법을 적용함:
    1. Period-wise batch inference : Period-conditional universal estimator를 통해 multiple period에 대해 parallel feed-forward 함
    2. Time-shared conditional Representation : Mel-spectrogram으로부터 추출하여 모든 step에서 사용함

Overall of PeriodWave

- Flow Matching for Waveform Generation

• Waveform generation을 위해 flow matching을 활용하는 경우 다음을 고려해야 함
  1. 먼저 $x_{0}$에 대한 적절한 noise scale을 설정해야 함
     • 일반적으로 waveform signal은 $[-1,1]$ (즉, standard normal distribution $\mathcal{N}(0,1)$)로 range 되므로 optimal path에서 큰 값을 가짐
       - 이로 인해 high-frequency information distrotion이 발생하므로 generated sample에는 low-frequency information만 포함됨
     • 따라서 논문은 small value $\alpha$를 multiplying 하여 $x_{0}$를 scale down 함
  2. Small $\alpha$를 적용하더라도 generated sample에는 small white noise가 포함될 수 있음 
     • 이를 해결하기 위해 논문은 $x_{0}$에 temperature $\tau$를 additionally multiplying 하여 사용함 
     • 추가적으로 PriorGrad의 data-dependent prior를 적용하여 flow matching-based generative model을 구성함
       - 이때 PeriodWave는 mel-spectrogram을 frequency-axis를 따라 averaging 하여 simply extract 될 수 있는 energy-based prior를 활용함
       
  3. 결과적으로 $p_{0}(x)$의 distribution에 대해 $\mathcal{N}(0,\Sigma)$를 설정하고 $\Sigma$에 small value $0.5$를 multiply 함
     - 이를 통해 sample quality를 개선하고 training speed를 높일 수 있음

- High-Frequency Information Modeling for Flow Matching

• Flow matching-based waveform generation model은 high-frequency information을 제공하기 어려우므로, 논문은 다음의 approach를 도입함
  1. Multi-band Flow Matching with Discrete Wavelet Transform
     • 논문은 signal을 disentangle 하고 information losing 없이 original signal을 reproduce 할 수 있는 Discrete Wavelet Transform-based Multi-band modeling method를 도입함 
     • 해당 PeriodWave-MB는 $[0\text{-}3, 3\text{-}6, 6\text{-}9, 9\text{-}12 \text{ kHz}]$의 각 band에 대한 multiple vector field estimator로 구성됨 
       - 이때 lower band를 생성한 다음 생성된 lower band를 $x_{0}$에 concatenate 해 higher band를 생성함
       - 이를 통해 small sampling step에서도 quality를 향상할 수 있음
     • Training 중에는 conditional information에 대한 ground-truth Discrete Wavelet Transform component를 활용함
       - 여기서 overlapped frequencey band $[0\text{-}61, 60\text{-}81, 80\text{-}93, 91\text{-}100 \text{ bins}]$를 포함하는 frequency axis를 따라 mel-spectrogram을 averaging 하여 band-wise data-dependent prior를 구성함
     • 추가적으로 first down/up-sampling을 DWT/iDWT로 대체하여 각 signal을 $[1,4,4]$ downsample 하고 time resolution을 reducing 하여 computational cost를 줄임 
  2. Flow Matching with FreeU
     • FreeU에서 skip connection의 feature는 UNet-based diffusion model에서 high-frequency information을 포함하고 있음
     • 마찬가지로 high-resolution waveform generation에서도 skip feature는 high-frequency information을 포함함
       - 특히 initial sampling step에서 UBlock에 noisy high-frequency information을 제공하므로 accumulate high-frequency noise는 waveform의 high-frequency information modeling을 방해함
     • 따라서 논문은 FreeU을 채택하여 skip feature $z_{skip}$를 scaling down 하고 backbone feature $x$를 scaling up 함:
       (Eq. 5) $x=\alpha\cdot z_{skip}+\beta\cdot x$
       - $\alpha=0.9, \beta=1.1$
       - Backbone feature를 scale up 하면 ground-truth mel-spectrogram에 포함된 noisy sound를 줄여 perceptual quality를 향상할 수 있음

3. Experiments

- Settings

• Dataset : LJSpeech, LibriTTS
• Comparisons : HiFi-GAN, BigVGAN, PriorGrad, FreGrad, WaveGlow, WaveFlow, UnivNet, Vocos

- Results

• PeriodWave는 기존보다 뛰어난 성능을 보임

LJSpeech에서의 성능

LibriTTS에서의 성능

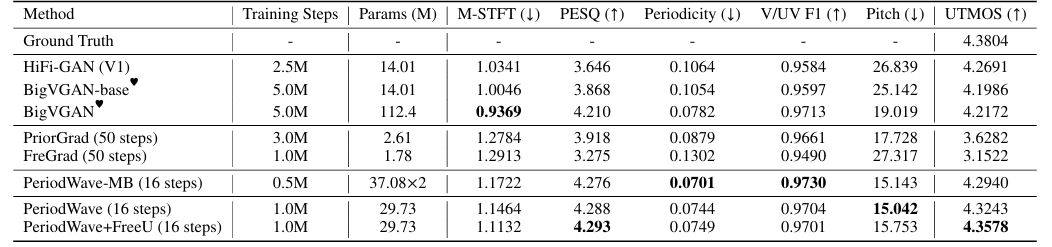
• Training step이 증가할수록 PeriodWave의 성능도 증가함

Training Step별 성능

• Sampling Robustness, Diversity, and Controllability
  • $\tau=0.667$의 temperature를 사용하는 경우 최적의 성능을 달성할 수 있음

Temperature $\tau$별 성능

• OOD Robustness
  • PeriodWave는 OOD dataset인 MUSDB18-HQ에 대해서도 robust 한 성능을 보임

MUSDB18-HQ에서의 성능

MUSDB18-HQ에서의 MOS 비교

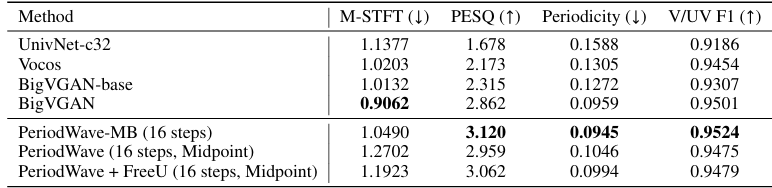
- Ablation Study

• Different Periods
  • Period가 $1$인 model의 성능이 가장 낮고, period 수가 증가할수록 성능이 일관적으로 향상됨
  • 특히 $[1,2,3,5,7]$과  같은 prime number의 period를 사용하는 경우 UTMOS를 보다 향상할 수 있음

Period별 성능

• CFM vs. Diffusion
  • PriorGrad의 prior-based diffusion과 비교하여 CFM이 더 나은 성능을 보임

CFM vs. Diffusion

• Multi-Speaker Text-to-Speech
  • BigVGAN, BigVSAN과 비교해 보면, PeriodWave가 더 우수한 MOS, UTMOS를 달성함

TTS 결과 비교

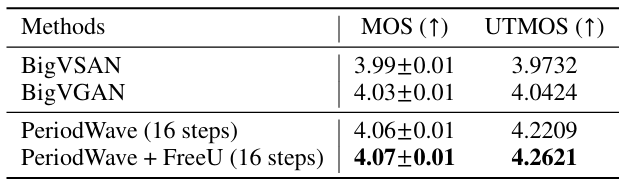
• Audio Generation from Discrete Token
  • Discrete token coding 측면에서도 PeriodWave는 뛰어난 성능을 보임

Discrete Token Parallel Generation

Discrete Token Streaming Generation