[Paper 리뷰] From Discrete Tokens to High-Fidelity Audio Using Multi-Band Diffusion

From Discrete Tokens to High-Fidelity Audio Using Multi-Band Diffusion

---

• Diffusion을 highly compressed representation으로 condition 된 audio waveform을 합성하는 데 사용할 수 있음
• MBD
  • Low-bitrate discrete representation에서 any type audio modality를 생성
  • 이를 위해 Multi-band diffusion-based framework를 활용
• 논문 (NeurIPS 2023) : Paper Link

---

1. Introduction

• MelGAN과 같은 neural-based vocoder는 high-quality sample을 합성할 수 있음
  • 특히 HuBERT와 같은 Self-Supervised Learning (SSL) method는 emotion, prosody information 등을 포함한 rich contextual representation을 얻는데 효과적임
    - 여기서 해당 representation을 활용하면 waveform quality를 더욱 향상할 수 있음
  • 이를 위해 기존에는 two-stage training pipeline을 활용하여 SSL audio representation을 먼저 학습하고, HiFi-GAN과 같은 Generative Adversarial Network (GAN) architecture를 통해 decoding을 수행함
    - BUT, 해당 방식은 training이 unstable 하고 output waveform에 audible artifact가 발생할 수 있음
  • 한편으로 SoundStream, DAC와 같은 compress model은 meaningful representation을 학습하기 위해 reconstruction loss를 활용함
    - 해당 compress model은 end-to-end 방식으로 training 되므로 다양한 audio domain에 적용될 수 있음

-> 그래서 discrete compressed representation으로부터 general audio에 대한 high-fidelity sample을 생성하는 MBD를 제안

 

• MBD
  • 서로 다른 frequency band를 independently process 하여 accumulative entangled error를 줄이는 Band-Specific Diffusion Model을 채택
  • Prior Gaussian distribution과 서로 다른 frequency band 간의 discrepancy를 reduce 하는 Frequency Equalizer (EQ) Process를 도입
  • Rich harmonic content를 가지는 audio data를 위해 Power Noise Scheduler를 설계

< Overall of MBD >

• Band-Specific Diffuion과 Frequency EQ Processor를 활용한 diffusion-based audio model
• 결과적으로 speech, music 등의 다양한 audio domain에서 기존보다 우수한 성능을 달성

2. Method

- Background

• DDPM을 따라 Markov chain $q$로 주어지는 diffusion process를 고려하자
  • 여기서 Gaussian noise는 standard Gaussian noise에 close 한 random variable $x_{T}$를 얻을 때까지 clean data point $x_{0}$에 gradually add 됨
    1. 먼저 full process에 대한 probability는:
       (Eq. 1) $q(x_{0:T}|x_{0})=\prod_{t=1}^{T}q(x_{t}|x_{t-1})$
       - $q(x_{t}|x_{t-1})\sim\mathcal{N}(\sqrt{1-\beta_{t}}x_{t-1}, \beta_{t}I), (\beta_{t})_{0\leq t\leq T}$ : noise schedule
    2. 이때 Markov chain $t$의 any step을 sampling 하면:
       (Eq. 2) $x_{t}=\sqrt{\bar{\alpha}_{t}}x_{0}+\sqrt{1-\bar{\alpha}_{t}}\epsilon $
       - $\bar{\alpha_{t}}=\prod_{s=0}^{t}(1-\beta_{s})$ : noise level, $\epsilon\sim\mathcal{N}(0,I)$
    3. 결과적으로 DDPM은 prior noise $x_{T}$에서 clean data point $x_{0}$로의 reverse process를 수행함:
       (Eq. 3) $p(x_{T:0})=p(x_{T})\prod_{t=1}^{T}p_{\theta}(x_{t-1}|x_{t})$
       - $p_{\theta}(x_{t}|x_{t-1})$ : diffusion chain $q(x_{t+1}|x_{t})$를 reverse 하는 learned distribution, $p(x_{T})$ : 학습되지 않은 prior distribution
       - Ideal noise schedule 하에서, (Eq. 2)의 prior distribution은 $\mathcal{N}(0,I)$에 approximate 함
       
  • 한편으로 $p_{\theta}(x_{t-1}|x_{t})$는 $\mathcal{N}(\mu_{\theta}(x_{t},t),\sigma_{t}I)$로 나타낼 수 있음
    1. $\mu_{\theta}$는 다음과 같이 reparameterize 됨:
       (Eq. 4) $\mu_{\theta}(x_{t},t)=\frac{1}{\sqrt{1-\beta_{t}}}\left(x_{t}-\frac{\beta_{t}}{\sqrt{1-\bar{\alpha}_{t}}}\epsilon_{\theta}(x_{t},t)\right)$
       - (Eq. 4)의 reparameterization은 neural network $\epsilon_{\theta}$가 corrupted data point $x_{t}$에서 noise를 predict 하도록 함
    2. 해당 neural network는 (Eq. 2)를 사용하여 $x_{t}$를 sampling 하고 다음의 $L2$ loss를 optimize 하여 training 됨:
       (Eq. 5) $\mathcal{L}=\mathbb{E}_{x_{0}\sim d(x_{0}),\epsilon\sim\mathcal{N}(0,I), t\sim\mathcal{U}\{1,...,T\}}\left(\left|\left| \epsilon-\epsilon_{\theta}\left( \sqrt{\bar{\alpha}_{t}}x_{0}+ \sqrt{1-\bar{\alpha}_{t}}\epsilon ,t\right)\right|\right|^{2}\right)$
       
    3. 결과적으로 다음의 (Eq. 6)을 iteratively use 하여 diffusion process를 reverse 할 수 있음:
       (Eq. 6) $x_{t-1}=\frac{1}{\sqrt{1-\beta_{t}}}\left(x_{t}-\frac{\beta_{t}}{\sqrt{1-\bar{\alpha}_{t}}}\epsilon_{\theta}(x_{t},t)\right) + \sqrt{\sigma_{t}}\epsilon $
       - $\sigma$ : $\tilde{\beta_{t}}=(1-\bar{\alpha}_{t-1})/(1-\bar{\alpha}_{t})$, $\beta_{t}$ 중에서 choice 되는 parameter 
       - 논문은 $\sigma_{t}=\tilde{\beta}_{t}$로 설정
       

Multi-Band Diffusion Process

- Multi-Band Diffusion

• Frequency EQ Processor
  • Prior Gaussian distribution과 target distribution에 대해 서로 다른 frequency band의 energy level을 balance 하는 것이 중요함
  • 먼저 white Gaussian noise signal은 모든 frequency에서 equal energy를 가지지만, natural sound는 동일한 distribution을 따르지 않음
    1. 특히 same scale signal의 경우 white noise는 common audio signal 보다 더 많은 energy를 가지고 있음
    2. 따라서 diffusion process를 동안 high-frequency part는 low-frequency counterpart보다 먼저 disappear 됨
       - 마찬가지로 reverse process 중에 (Eq. 6)을 통해 주어진 noise addition은 high-frequency에 더 많은 영향을 미침
  • 이를 해결하기 위해 논문은 multiple frequency band에 걸쳐 clean energy signal을 normalize 하여 $x_{0}$을 얻음
    1. 다음으로 $x_{0}$를 mel-scale에서 equally space 된 band pass filter의 cascade를 통해 $B$ component $b_{i}$로 split 함
    2. Audio signal의 filtered band $b_{i}$가 주어지면, 다음과 같이 normalize 됨:
       (Eq. 7) $\hat{b}_{i}=b_{i}\cdot\left(\frac{\sigma_{i}^{\epsilon}}{\sigma_{i}^{d}}\right)^{\rho}$
       - $\sigma_{i}^{\epsilon},\sigma_{i}^{d}$ : 각각 standard Gaussian noise, dataset signal에 대한 band $i$의 energy 
       - $\rho$ : energy level align을 control 하는 역할 ($\rho=0$인 경우 processor는 rebalancing을 수행하지 않고, $\rho=1$인 경우 target energy와 exactly matching 되도록 함)
    3. 한편으로 speech signal은 high-frequency band의 content를 가지지 않을 수 있으므로, (Eq. 7)에서 instability를 avoid 하기 위해 music domain에서 $\sigma_{i}^{d}$를 compute 함 

Mel Scale Frequency Band 별 Standard Deviation

• Scheduler Tuning
  • Noise schedule은 diffusion model에서 important hyperparameter set를 entail 하고 generation의 final quality에 중요한 역할을 함
    1. BUT, 일반적으로 raw waveform generation의 경우 high sampling rate에 적합하지 않은 linear나 cosine schedule을 사용함 
       
    2. 따라서 논문은 다음의 $p$-power schedule을 채택함:
       (Eq. 8) $\beta_{t}=\left(\sqrt[p]{\beta_{0}}+\frac{t}{T}\left(\sqrt[p]{\beta_{T}}-\sqrt[p]{\beta_{0}}\right)\right)^{p}$
       - 여기서 first, last step ($\beta_{0},\beta_{T}$)에서 injected noise의 variance는 hyperparameter로 취급됨
  • 이때 generation time에 사용되는 noise schedule은 training 이후에 choice 될 수 있으므로 training noise schedule을 tuning 할 필요가 없고, subset $S$의 choice에만 focus 할 수 있음 
    1. Train-time은 uniformly sample 되므로 training noise schedule은 noise level $\sqrt{\bar{\alpha}}$의 sampling distribution을 parameterize 함
    2. 실제로 아래 그림과 같이 해당 power schedule을 사용하면, training example은 매우 작은 noise (매우 높은 $\bar{\alpha}$)를 sampling 할 수 있음
  • 추가적으로 $T$에 close 한 time step $t$를 가지는 diffusion process end에서 model estimate $\epsilon_{\theta}(x_{t})$를 사용하는 것이 $x_{t}$ 보다 더 나쁠 수 있음
    1. 이는 model training 과정의 limited precision 때문
       - 특히 model은 identity function으로 replace 되므로 해당 time step을 entirely skipping 할 수 있음
       
    2. 따라서 $\sqrt{1-\alpha_{t}}$가 해당 phenomenon을 avoid 할 수 있도록 $\beta_{t}$를 choice 함 

(좌) Cosine/Power Schedule의 Noise Level (우) Diffusion Process의 Spectrogram

• Band-Specific Training
  • Audio diffusion model은 low-frequency를 먼저 생성한 다음, reverse process에서 high-frequency를 처리함
    1. 특히 audio data에는 time, frequency에 대한 spectrogram content의 complex entanglement가 존재함
    2. 이때 full-band audio data에 대해 diffusion model을 training 하면, high-frequency를 생성할 때 항상 ground-truth low-frequency가 제공됨
       - 결과적으로 reverse process에서 generation beginning에 commit 된 error가 amplify 될 수 있음
  • 따라서 논문은 각 frequency band를 independently training 하여 perceptual quality를 향상함
  • 한편으로 model channel을 따라 frequency band를 divide 하는 경우, 성능 향상이 나타나지 않음
    - 이는 previously generated content (low-frequency)를 제공하지 않으면 sampling 중에 error accumulation을 방지할 수 있음을 의미함

3. Experiments

- Settings

• Dataset : CommonVoice7, DNS Challenge4, MTG-Jamendo, FSD50K, AudioSet
• Comparisons : EnCodec, OPUS

- Results

• 전체적으로 MBD의 성능이 가장 우수함

Model 성능 비교

• DAC, HiFi-GAN, PriorGrad와의 비교에서도 MBD는 가장 우수한 성능을 보임

Decoder Baseline 비교

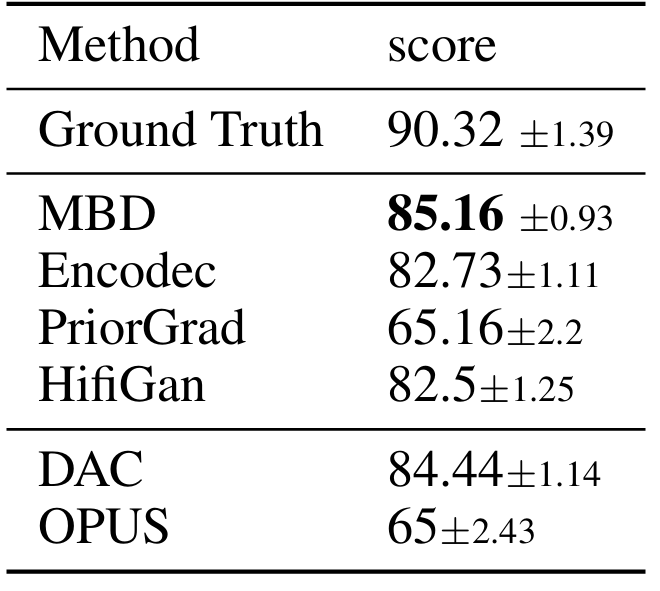
• Ablations
  • MBD는 objective metric 측면에서 더 나은 reconstruction 성능을 달성함

Reconstruction 성능

• 추가적으로 각 component를 대체하는 경우 성능 저하가 발생함

Ablation Study

• Text-to-Audio
  • MusicGen과 Bark에 각각 MBD를 적용했을 때, 기존보다 더 나은 MUSHRA score를 달성함

Text-to-Audio