[Paper 리뷰] Shallow Flow Matching for Coarse-to-Fine Text-to-Speech Synthesis

Shallow Flow Matching for Coarse-to-Fine Text-to-Speech Synthesis

---

• Flow Matching-based Text-to-Speech model을 개선할 수 있음
• Shallow Flow Matching (SFM)
  • Coarse representation으로부터 Flow Matching path를 따라 intermediate state를 construct
  • 해당 state의 temporal position을 adaptively determine 하기 위해 orthogonal projection을 도입
• 논문 (NeurIPS 2025) : Paper Link

---

1. Introduction

• VoiceBox, ReFlow-TTS, VoiceFlow와 같은 Flow Matching (FM)-based Text-to-Speech (TTS) model은 coarse-to-fine generation paradigm을 주로 활용함
  • 즉, weak generator가 input context에 condition 된 coarse representation을 생성하고 FM module을 통해 high-quality mel-spectrogram으로 refine 한 다음 vocoder를 통해 waveform으로 convert 함
  • 이때 weak generator의 경우 다음 2가지 방식을 고려할 수 있음:
    1. Grad-TTS, Matcha-TTS와 같이 non-autoregressive encoder와 alignment module을 활용하여 coarse mel-spectrogram을 jointly generate 하는 방식
    2. CosyVoice, CosyVoice2와 같이 autoregressive Large Language Model (LLM)을 context processor와 weak generator로 사용하여 discrete speech token을 generate 하는 방식
  • 특히 coarse-to-fine FM-based TTS에서 coarse representation은 flow module의 condition으로 사용됨
    - BUT, generation은 pure noise에서 시작하므로 modeling capacity의 suboptimal allocation이 발생함

-> 그래서 coarse representation 기반의 FM path를 construct 하는 Shallow Flow Matching (SFM)을 제안

 

• SFM
  • DiffSinger의 shallow diffusion mechanism을 확장하여 coarse representation을 기반으로 FM path를 따라 intermediate state를 construct
  • Orthogonal projection을 사용하여 time을 adaptively determine 하고 single-segment piecewise flow를 formulate

< Overall of SFM >

• Shallow diffusion mechanism를 Flow Matching으로 확장한 coarse-to-fine modeling method
• 결과적으로 기존보다 우수한 성능을 달성

2. Preliminaries

- Flow Matching

• Time-dependent diffeomorphic map $\phi_{t}:[0,1]\times \mathbb{R}^{d}\rightarrow \mathbb{R}^{d}$는 time $t\in [0,1]$에 따른 data point $x\in\mathbb{R}^{d}$의 smooth, invertible transformation을 describe 함
  • 이때 flow는 time-dependent Vector Field (VF) $u_{t}:[0,1]\times \mathbb{R}^{d}\rightarrow \mathbb{R}^{d}$를 통한 Ordinary Differential Equation (ODE)로 정의됨:
    (Eq. 1) $ x_{t}=\phi_{t}(x_{0}),\,\,\,\frac{d}{dt}\phi_{t}(x_{0})=u_{t}(\phi_{t}(x_{0}))$
    
  • VF $u_{t}$는 time-dependent Probability Density Function (PDF)인 probability density path $p_{t}:[0,1]\times \mathbb{R}^{d}\rightarrow \mathbb{R}^{d}$를 induce 함
    - Time $0$에서 $t$까지 $x$의 PDF는 $u_{t}$를 따라 $p_{0}(x_{0})$에서 $p_{t}(x_{t})$로 transport 됨
  • 그러면 learnable parameter $\theta$에 대해 Continuous Normalizing Flow (CNF)는 $u_{t}$를 neural network $v_{\theta}(x_{t},t)$로 modeling 할 수 있음
    - CNF는 simple prior distribution $p_{0}$를 complicated distribution $p_{1}$으로 reshape 함
  • 이를 확장하여 objective가 $\mathcal{L}_{FM}=\mathbb{E}_{t, p_{t}(x_{t})}|| v_{\theta}(x_{t},t)-\mu_{t}(x_{t})||^{2}$인 Flow Matching (FM)을 고려할 수 있음
    
    1. 이때 FM은 appropriate $p_{t}, u_{t}$가 unknown이므로 data sample $x_{1}\sim q(x_{1})$에 condition 된 probability path를 construct 함
       - 즉, $p_{0}(x_{0})=\mathcal{N}(x_{0}|0,I), p_{1}(x_{1})\approx q(x_{1})$이라고 하면 conditional probability path는 $p_{t}(x_{t}|x_{1})=\mathcal{N}(x_{t}|\mu_{t}(x_{1}),\sigma_{t}(x_{1})^{2}I)$와 같음
    2. 결과적으로 flow와 VF를 formulate 하면:
       (Eq. 2) $\phi_{t}(x_{t})=\sigma_{t}(x_{1})x_{t}+\mu_{t}(x_{1}),\,\,\, u_{t}(x_{t}|x_{1})=\frac{\sigma'_{t}(x_{1})}{\sigma_{t}(x_{1})}(x_{t}-\mu_{t}(x_{1}))+\mu'_{t}(x_{1})$
       - $\mu_{t}:[0,1]\times \mathbb{R}^{d}\rightarrow \mathbb{R}^{d}$ : time-dependent mean
       - $\sigma_{t}:[0,1]\times \mathbb{R}^{d}\rightarrow \mathbb{R}_{>0}$ : time-dependent scalar standard deviation (std)
       - $f'$ : time에 대한 derivative, $f'=\frac{d}{dt}f$
    3. Optimal Transport (OT) displacement interpolant에 대한 mean과 std는:
       (Eq. 3) $\mu_{t}(x_{1})=tx_{1},\,\,\,\sigma_{t}(x_{1})=1-(1-\sigma_{\min})t$
       - $\sigma_{\min}$ : sufficiently small value, 
    4. (Eq. 3)에 (Eq. 2)를 대입하면, conditional flow와 VF를 얻을 수 있음:
       (Eq. 4) $\phi_{t}(x_{0})=(1-t)x_{0}+t(x_{1}+\sigma_{\min}x_{0}),\,\,\, u_{t}(x_{t}|x_{1})=(x_{1}+\sigma_{\min}x_{0})-x_{0}$
       
    5. 그러면 training 중에 Conditional Flow Matching (CFM) loss를 minimize 할 수 있고, 이는 FM loss $\mathcal{L}_{CFM}=\mathbb{E}_{t,p_{t}(x_{t})}|| v_{\theta}(x_{t},t)-u_{t}(x_{t}|x_{1})||^{2}$를 minimize 하는 것과 equivalent 함
       - 추론 시에는 ODE solver를 사용하여 integral $x_{pred}=x_{0}+\int_{0}^{1}v_{\theta}(x_{t},t)dt$를 solve 함

- Classifier-Free Guidance

• FM-based generative model에서는 generation process를 control 하기 위해 training/inference 중에 input condition $c$를 incorporate 할 수 있음
  • 특히 diversity와 fidelity를 위해 Classifier-Free Guidance (CFG)가 자주 사용됨
  • CFG는 training 중에 condition $c$를 randomly drop 하여 model이 conditional/unconditional context에서 학습되도록 함
  • 추론 시에는 CFG strength $\beta>0$을 활용하여 trade-off를 control 함:
    (Eq. 5) $ v_{\theta,\text{CFG}}(x_{t},t,c)=v_{\theta}(x_{t},t,c)+\beta(v_{\theta}(x_{t},t,c) -(v_{\theta}(x_{t},t)))$
    - FM module은 각 time step 마다 $c$를 포함/포함하지 않는 2번의 forward pass를 수행함

3. Method

- Theorems

• [Theorem 1] $t_{m}\in [0,\infty), \sigma_{m}\in (0,\infty)$인 임의의 random variable $x_{m}\sim \mathcal{N}(t_{m}x_{1},\sigma_{m}^{2}I)$에 대해 $x_{m}$을 conditional OT (CondOT) path에 mapping 하는 transformation을 정의하자. 이때 output distribution은 Wasserstein-2 metric 하에서 $t_{m}, \sigma_{m}$에 대해 continuously vary 함:
  (Eq. 6) $ \Delta=(1-\sigma_{\min})t_{m}+\sigma_{m}$
  (Eq. 7) $x_{\tau}=\left\{\begin{matrix}
  \sqrt{(1-(1-\sigma_{\min})t_{m})^{2}-\sigma^{2}_{m}}x_{0}+x_{m}, & \text{if}\,\,\Delta <1 \\
  \frac{1}{\Delta}x_{m}, &  \text{if}\,\, \Delta\geq 1\\
  \end{matrix}\right.$
  - $x_{0}\sim \mathcal{N}(0,I)$, $\tau=\min (t_{m},\frac{t_{m}}{\Delta})$
• [Theorem 2] CondOT path 상의 arbitrary intermediate state에 대해:
  (Eq. 8) $x_{t_{m}}=(1-t_{m})x_{0}+t_{m}(x_{1}+\sigma_{\min}x_{0}),\,\,\, t_{m}\in(0,1),x_{0}\sim \mathcal{N}(0,I)$
  Path를 $t_{m}$에서 두 segment로 divide 할 수 있고, flow와 VF를 piecewise function으로 represent 할 수 있음:
  (Eq. 9) $x_{t}=\left\{\begin{matrix}
  (1-\frac{t}{t_{m}})x_{0}+\frac{t}{t_{m}}x_{t_{m}}, & \text{if}\,\,t<t_{m} \\
  (1-\frac{t-t_{m}}{1-t_{m}})x_{t_{m}}+\frac{t-t_{m}}{1-t_{m}}(x_{1}+\sigma_{\min}x_{0}), & \text{if}\,\,t\geq t_{m} \\
  \end{matrix}\right.$
  (Eq. 10) $u_{t}=\left\{\begin{matrix}
  \frac{1}{t_{m}}(x_{t_{m}}-x_{0}), & \text{if}\,\,t<t_{m}  \\
  \frac{1}{1-t_{m}}(x_{1}+\sigma_{\min}x_{0}-x_{t_{m}}), & \text{if}\,\,t\geq t_{m} \\
  \end{matrix}\right.$

ODE Solver

- Coarse-to-Fine FM-based TTS

• Time frame 수 $N$, frequency bin (channel) 수 $F$에 대해 audio waveform의 mel-spectrogram을 $\mathbf{X}\in \mathbb{R}^{N\times F}$라고 하자
  • 그러면 $\mathbf{X}^{n}\in\mathbb{R}^{F}$는 $n$-th mel-spectrogram frame을 나타냄
    1. Learnable parameter $\omega$에 대해 weak generator $g_{\omega}$는 text, speaker feature, contextual information을 input condition $\mathbf{C}$로 사용하여 coarse mel-spectrogram $\hat{\mathbf{X}}_{g}$를 output 함
    2. $\hat{\mathbf{X}}_{g}$는 $L2$ loss를 사용하여 target sample $\mathbf{X}_{1}$과 match 되도록 supervise 됨:
       (Eq. 11) $\mathcal{L}_{\text{coarse}}=\mathbb{E}||\hat{\mathbf{X}}_{g}-\mathbf{X}_{1}||^{2}$
  • Learnable parameter $\psi$를 가지는 lightweight SFM head $h_{\psi}$는 $g_{\omega}$의 final hidden state $\hat{\mathbf{H}}_{g}$를 input으로 하여 scaled mel-spectrogram $\hat{\mathbf{X}}_{h}$를 output 함
    - 여기서 $\hat{\mathbf{X}}_{g}$는 $\hat{\mathbf{H}}_{g}$에 linear projection을 적용하여 얻어짐
  • 추가적으로 $h_{\psi}$는 $\hat{\mathbf{X}}_{h}$에 대해 time $\hat{t}_{h}\in (0,1)$과 estimated variance $\hat{\sigma}_{h}^{2}$를 predict 해야 함:
    (Eq. 12) $ \hat{\mathbf{H}}_{g},\hat{\mathbf{X}}_{g}=g_{\omega}(\mathbf{C}),\,\,\, \hat{\mathbf{X}}_{h},\hat{t}_{h},\hat{\sigma}_{h}^{2}=h_{\psi}(\hat{\mathbf{H}}_{g})$

SFM Head

- Orthogonal Projection onto CondOT Paths

• CondOT path 상에서 $\hat{\mathbf{X}}_{h}$의 exact location과 해당 time $t_{h}$는 unknown이므로, 논문은 model이 training 시 $t_{h}$를 adaptively determine 하도록 함
  • 먼저 $\hat{\mathbf{X}}_{h}$를 CondOT path로 direct 하기 위해 $\hat{\mathbf{X}}_{h}$에서 $\mathbf{X}_{1}$로의 orthogonal projection을 find 함
    - (Eq. 3)에 따라 projection coefficient는 $t_{h}$와 같고, 이는 mean path $\mu_{t}(\mathbf{X}_{1})$ 상의 intermediate state에 해당함
  • 이후 time $t_{h}$와 variance $\sigma^{2}_{h}$를 estimate 하고 loss $\mathcal{L}_{\mu}$를 통해 $\hat{\mathbf{X}}_{h}, t_{h}\mathbf{X}_{1}$ 간의 distance를 minimize 함:
    (Eq. 13) $t_{h}=\max\left(0,\mathbb{E}\left[\frac{\text{sg}[\hat{\mathbf{X}}_{h}]\cdot \mathbf{X}_{1}}{\mathbf{X}_{1}\cdot\mathbf{X}_{1}}\right]\right),\,\,\, \sigma^{2}_{h}=\mathbb{E}\left|\left| \text{sg}[\hat{\mathbf{X}}_{h}]-t_{h}\mathbf{X}_{1}\right|\right|^{2},\,\,\, \mathcal{L}_{\mu}=\mathbb{E}\left|\left| \hat{\mathbf{X}}_{h}-t_{h}\mathbf{X}_{1}\right|\right|^{2}$
    - $\text{sg}[\cdot]$ : stop gradient, $\sigma^{2}_{h}$ : $\hat{\mathbf{X}}_{h}$의 noise scale로써 intrinsic noise로 볼 수 있음
  • $\hat{\mathbf{X}}_{h}\approx t_{h}\mathbf{X}_{1}$이면 $\hat{\mathbf{X}}_{h}\sim \mathcal{N}(t_{h}\mathbf{X}_{1},\sigma^{2}_{h}I)$를 가정하고 CondOT path에서 intermediate state를 construct 하기 위해 [Theorem 1]을 적용할 수 있음:
    (Eq. 14) $\Delta=\max\left((1-\sigma_{\min})t_{h}+\sigma_{h},1\right),\,\, \tilde{\mathbf{X}}_{h}=\frac{1}{\Delta}\hat{\mathbf{X}}_{h},\,\,\tilde{t}_{h}=\frac{1}{\Delta}t_{h},\,\, \tilde{\sigma}_{h}^{2}=\frac{1}{\Delta^{2}}\sigma^{2}_{h}$
    (Eq. 15) $\mathbf{X}_{\tilde{t}_{h}}=\sqrt{\max\left((1-(1-\sigma_{\min})\tilde{t}_{h})^{2}-\tilde{\sigma}_{h}^{2}, 0\right)}\mathbf{X}_{0}+\tilde{\mathbf{X}}_{h}$
    - $\mathbf{X}_{0}\sim \mathcal{N}(0,I)$
  • Early training stage에서는 $\Delta\geq 1$일 수 있는데, 이 경우 $\hat{\mathbf{X}}_{h}$는 external noise $\mathbf{X}_{0}$와 함께 CondOT path 상에 lie 할 수 없으므로 deterministic model behavior가 발생함
    1. 따라서 [Theorem 1]의 scaling factor $\frac{1}{\Delta}$는 $\hat{\mathbf{X}}_{h}$를 CondOT path로 rescale 하여 $\mathbf{X}_{0}$를 incorporate 할 수 있도록 함
    2. 그러면 두 predicted scalar에 대한 loss는 다음과 같이 얻어짐:
       (Eq. 16) $\mathcal{L}_{t}=(\hat{t}_{h}-\tilde{t}_{h})^{2},\,\,\, \mathcal{L}_{\sigma}=(\hat{\sigma}_{h}^{2}-\tilde{\sigma}_{h}^{2})^{2}$

Inference Process

- Single-Segment Piecewise Flow

• Training/inference 시 flow는 $\tilde{h}_{t}$에서 시작함
  • 따라서 논문은 [Theorem 2]를 사용하여 path의 second segment ($t\geq \tilde{t}_{h}$)에 focus 함:
    (Eq. 17) $ t_{\mathcal{U}}\sim\mathcal{U}[0,1],\,\, t_{\mathcal{S}}=\mathcal{S}(t_{\mathcal{U}}),\,\, t=(1-\tilde{t}_{h})t_{\mathcal{S}}+\tilde{t}_{h}$
    (Eq. 18) $\mathbf{X}_{t}=\left(1-\frac{t-\tilde{t}_{h}}{1-\tilde{t}_{h}}\right)\mathbf{X}_{\tilde{t}_{h}} +\frac{t-\tilde{t}_{h}}{1-\tilde{t}_{h}}(\mathbf{X}_{1}-\sigma_{\min}\mathbf{X}_{0})$
    (Eq. 19) $\,\,\,\,\,\,\,\,\, =(1-t_{\mathcal{S}})\mathbf{X}_{\tilde{t}_{h}}+t_{\mathcal{S}}(\mathbf{X}_{1}+\sigma_{\min}\mathbf{X}_{0})$
    (Eq. 20) $\mathbf{U}_{t}=\frac{1}{1-\tilde{t}_{h}}(\mathbf{X}_{1}+\sigma_{\min}\mathbf{X}_{0}-\mathbf{X}_{\tilde{t}_{h}})$
    - $\mathcal{S}$ : randomly sampled $t$에 대한 arbitrary time scheduler
  • SFM framework의 overall loss는:
    (Eq. 21) $\mathcal{L}_{CFM}=\mathbb{E}_{t,p_{t}(\mathbf{X}_{t})} || v_{\theta}(\mathbf{X}_{t},t)-\mathbf{U}_{t}||^{2},\,\,\, \mathcal{L}_{SFM}=\mathcal{L}_{coarse}+\mathcal{L}_{t}+\mathcal{L}_{\sigma}+\mathcal{L}_{\mu}+\mathcal{L}_{CFM}$

Training Procedure

- Inference with SFM Strength

• 추론 시 adaptively determined $t_{h}$가 작아지는 경향이 있으므로 prior information이 limit 됨
  • 이를 해결하기 위해 논문은 SFM strength $\alpha\geq 1$을 도입하여 $\hat{t}_{h}$를 scale up 하고 $\hat{\mathbf{X}}_{h}$로부터의 stronger guidance를 보장함:
    (Eq. 22) $\Delta=\max\left(\alpha\left( (1-\sigma_{\min})\hat{t}_{h}+\hat{\sigma}_{h}\right),1\right), \,\, \tilde{\mathbf{X}}_{h}=\frac{\alpha}{\Delta}\hat{\mathbf{X}}_{h},\,\, \tilde{t}_{h}=\frac{\alpha}{\Delta}\hat{t}_{h},\,\, \tilde{\sigma}_{h}^{2}=\frac{\alpha^{2}}{\Delta^{2}}\hat{\sigma}_{h}^{2}$
  • (Eq. 15)에 $\tilde{\mathbf{X}}_{h},\tilde{t}_{h},\tilde{\sigma}_{h}^{2}$를 대입하면 $\mathbf{X}_{\tilde{t}_{h}}$를 얻을 수 있고, integral $\mathbf{X}_{pred}=\mathbf{X}_{\tilde{t}_{h}}+\int_{\tilde{t}_{h}}^{1}v_{\theta}(\mathbf{X}_{t},t)dt$를 ODE solver를 통해 solve 하면 predicted result $\mathbf{X}_{pred}$를 얻을 수 있음
  • 논문은 각 model에 SFM method를 적용하여 optimal $\alpha$를 determine 함
    1. 대부분의 경우 optimal $\alpha$는 relatively small 하므로 $\Delta=1$이 됨
    2. Scaling factor $\frac{\alpha}{\Delta}$는 theoretical upper bound로 $\frac{1}{(1-\sigma_{\min})\hat{t}_{h}+\hat{\sigma}_{h}}$를 가짐

Inference Procedure

4. Experiments

- Settings

• Dataset : LJSpeech, VCTK, LibriTTS
• Comparisons : Matcha-TTS, CosyVoice, StableTTS

Baseline Configuration

- Results

• 전체적으로 SFM을 사용했을 때 더 나은 성능을 달성함

Model 성능 비교

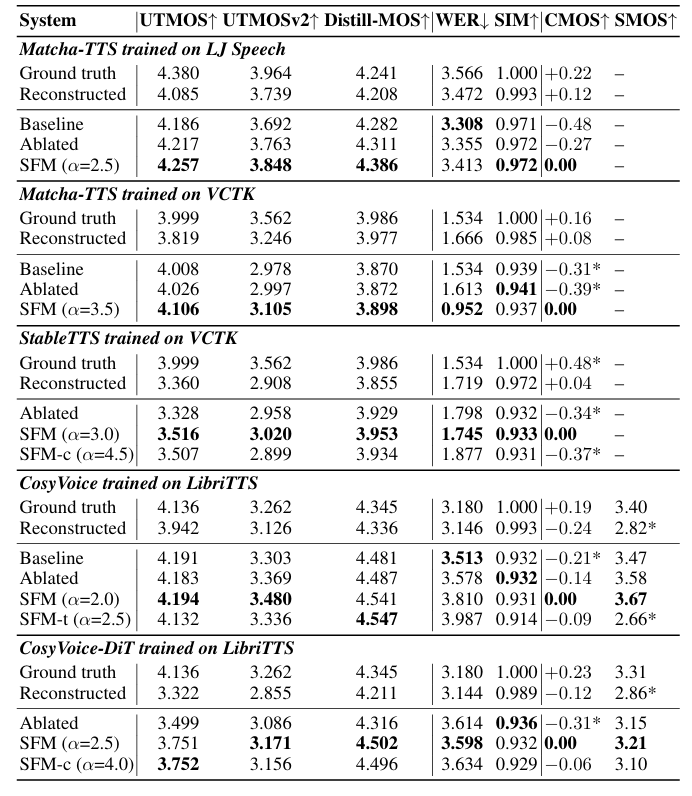
• $\alpha=2.5$에서 최적의 성능을 달성함

$\alpha$ Selection

• RTF 측면에서도 baseline 보다 빠른 속도를 보임

RTF 비교