[Paper 리뷰] Grad-TTS: A Diffusion Probabilistic Model for Text-to-Speech

Grad-TTS: A Diffusion Probabilistic Model for Text-to-Speech

---

• Denoising diffuion probabilistic model과 generative score matching은 복잡한 data 분포를 모델링하는데 뛰어남
• Grad-TTS
  • Encoder에 의해 예측된 noise를 점진적으로 변환하고 Monotonic Alignment Search를 통해 text input에 맞춰 정렬된 mel-spectrogram을 생성
  • Stochastic differential equation을 통해 noise로부터 data를 reconstruct
• 논문 (ICML 2021) : Paper Link

---

1. Introduction

• Text-to-Speech (TTS) 모델은 two-stage 방식으로 설계되는 경우가 많음
  1. Feature Generator : input text를 time-frequency domain acoustic feature로 변환
     - Feature generator로써 Tacotron2, Transformer-TTS가 우수한 성능을 보였지만 상당히 계산 비효율적임
     - FastSpeech의 경우 non-autoregressive architecture를 활용하고 monotonic alignment를 적용하여 pronunciation robstness를 향상 가능
     - BUT, character duration을 학습하기 위해 teacher model의 pre-computed alignment를 필요로 함
  2. Vocoder : Conditioned feature로부터 raw waveform을 합성
     - 고품질 음성을 합성에서도 parallel non-autoregressive vocoder들이 주로 활용됨
     - WaveGlow는 Normalizing Flow를 활용하여 빠른 합성 속도를 달성했지만, GPU와 같은 특정 device에서만 가능함
     - HiFi-GAN, Mel-GAN과 같이 Generative Adversarial Network (GAN)을 활용하는 방식들도 있음  
• Normalizing Flow를 활용한 Glow-TTS는 pronunciation 문제와 latency 문제를 해결할 수 있음
  • Glow-TTS는 input text를 mel-spectrogram에 mapping 하기 위해 Monotonic Alignment Search (MAS)를 도입
    - MAS를 통해 Tacotron2와 같은 autoregressive 방식의 pronunciation 문제를 해결
    - 추가적으로 Glow-TTS는 병렬 합성을 가능하게 하여 빠른 추론 속도를 달성했음
  • 특히 Glow-TTS는 FastSpeech와 달리 MAS가 unsupervised 방식으로 동작하여 token duration에 대한 external aligner를 필요로 하지 않음
• 최근에는 Diffusion Proobabilistic Model (DPM)의 등장으로 복잡한 data를 효과적으로 모델링할 수 있게 됨
  • DPM의 기본 idea:
    1. Simple 분포(일반적으로 표준 정규 분포)를 얻을 때까지 original data를 반복적으로 변환하는 forward diffusion process를 구축하고
    2. Reverse-time forward diffusion trajectory를 따르도록 parameterize 된 neural network를 구축
  • 추론 시에는 numerical differential equation solver를 기반으로 활용
  • 이를 활용하여 WaveGrad와 DiffWave는 vocoder 작업에서 유망한 raw waveform reconstruction 성능을 보임
    -> BUT, feature generator 측면에서는 DPM을 활용한 방식들이 아직 제시되지 않음 

-> 그래서 diffusion probabilistic modelling을 활용하는 acoustic feature generator인 Grad-TTS를 제안

 

• Grad-TTS
  • MAS-aligned encoder output을 decoder로 전달되어 Gaussian noise를 mel-spectrogram으로 변환
  • Gaussian noise로부터 data를 reconstruct 하기 위해 forward/reverse diffusion에 대한 generalized version을 활용
  • 특히 Grad-TTS는 output mel-spectrogram 품질과 추론 속도 간의 trade-off를 명시적으로 제어 가능

< Overall of Grad-TTS >

• Encoder에 의해 예측된 noise를 점진적으로 변환하고 Monotonic Alignment Search를 통해 text input에 맞춰 정렬된 mel-spectrogram을 생성
• 결과적으로 10번의 reverse diffusion 만으로도 고품질의 mel-spectrogram을 생성 가능하고, 추론 속도 측면에서 Tacotron2 보다 빠른 속도를 보임

2. Diffusion Probabilistic Modelling

• Diffusion process는 Stochastic Differential Equation (SDE)를 만족하는 stochastic process라고 할 수 있음:
  (Eq. 1) $dX_{t} = b(X_{t}, t) dt + a(X_{t}, t) dW_{t}$
  - $W_{t}$ : standard Brownian motion, 유한 시간 범위 $T$ 내에서 $t \in [0,T]$
  - $b, a$ : 각각 drift, diffusion coefficient
  
• 임의의 inital data 분포 $Law(X_{0})$에 대해 $T \rightarrow \infty$일 때 최종적인 분포 $Law(X_{T})$가 standard Normal $\mathcal{N}(0,I)$로 수렴하는 forward process를 고려할 수 있음
  • $I$ : $n\times n$ identity matrix, $n$ : data dimensionality
  • 이러한 특성을 가지는 모든 diffusion process를 forward process라고 하고, diffusion probabilistic modelling의 목표는 trajectory가 forward process와 비슷하지만 time order는 반대인 reverse diffusion을 찾는 것
    - Reverse diffusion은 forward diffusion보다 어렵지만, 적절한 neural network를 사용하여 reverse diffusion을 parameterize 하는 것으로 해결할 수 있음
    - 이를 위해 일반적으로 $\mathcal{N}(0,I)$에서 random noise를 sampling 한 다음, first-order Euler-Maruyama scheme과 같은 numerical solver를 사용함
  • Forward와 reverse diffusion process의 trajectory가 가까운 경우, sample 분포는 data $Law(X_{0})$의 분포와 매우 유사함
• Score-based / Denoising diffusion probabilistic model은 주로 Markov chain으로 formalize 됨
  • BUT, Markov chain은 특정 SDE를 만족하는 stochastic process의 trajectory에 근사될 수 있다는 것이 입증됨
  • 따라서 Grad-TTS는 Markov chain을 사용하지 않고 SDE 측면에서 diffusion probabilistic model (DPM)을 정의
    - Infinite time horizon에 대해 forward diffusion이 모든 data 분포를 $\mathcal{N}(0,I)$ 대신, 주어진 평균 $\mu$와 diagonal covariance matrix $\Sigma$에 대한 $\mathcal{N}(\mu, \Sigma)$로 변환하는 방식으로 DPM을 generalize

Diffusion Probabilistic Modelling의 과정

- Forward Diffusion 

• 먼저 Infinite time horizon $T$가 주어졌을 때, data를 Gaussian noise로 변환하는 forward diffusion process를 정의하자.
  1. $n$-dimensional stochsatic process $X_{t}$가 다음의 SDE를 만족한다면:
     (Eq. 2) $dX_{t} = \frac{1}{2}\Sigma^{-1}(\mu-X_{t})\beta_{t}dt +\sqrt{\beta_{t}}dW_{t}, \,\,\, t \in [0,T]$
  2. Non-negative function $\beta_{t}$ (noise schedule)에 대해, vector $\mu$와 positive element를 가지는 diagonal matrix $\Sigma$에 대한 solution은:
     (Eq. 3) $X_{t} = \left( I - e^{-\frac{1}{2}\Sigma^{-1}\int^{t}_{0}\beta_{s}ds}\right)\mu + e^{-\frac{1}{2}\Sigma^{-1}\int_{0}^{t}\beta_{s}ds}X_{0} + \int_{0}^{t}\sqrt{\beta_{s}}e^{-\frac{1}{2}\Sigma^{-1}\beta_{u}du}dW_{s}$ 
  3. 이때 diagonal matrix의 exponential은 element-wise exponential이므로,
     (Eq. 4) $\rho(X_{0},\Sigma,\mu,t) = \left( I-e^{-\frac{1}{2}\Sigma^{-1}\int_{0}^{t}\beta_{s}ds}\right)\mu + e^{-\frac{1}{2}\Sigma^{-1}\int_{0}^{t}\beta_{s}ds}X_{0}$
     (Eq. 5) $\lambda(\Sigma,t)= \Sigma \left( I- e^{-\Sigma^{-1}\int_{0}^{t}\beta_{s}ds}\right)$
  4. $X_{0}$가 주어졌을 때, $X_{t}$의 integral condition 분포는 Ito's property에 의해 Gaussian임:
     (Eq. 6) $Law(X_{t}|X_{0}) = \mathcal{N}(\rho(X_{0},\Sigma,\mu,t), \lambda(\Sigma,t))$
  5. 이는 infinite time horizon을 고려했을 때, 어떠한 noise shcedule $\beta_{t}$에 대해서도 $\displaystyle \lim_{t \to \infty} e^{-\int_{0}^{t}\beta_{s}ds}=0$이라는 것을 의미하므로:
     (Eq. 7) $X_{t}|X_{0} \overset{d}{\rightarrow} \mathcal{N}(\mu, \Sigma)$
• 위에 따라 random variable $X_{t}$는 $X_{0}$와 독립적으로 $\mathcal{N}(\mu, \Sigma)$로 수렴함
  - 결과적으로 (Eq. 2)를 만족하는 forward diffusion은 data 분포 $Law(X_{0})$를 Gaussian noise $\mathcal{N}(\mu, \Sigma)$로 변환된다는 property를 얻음

- Reverse Diffusion 

• DPM의 reverse diffusion은 reverse-time dynamics에 대한 명시적인 formula로써
  • 아래의 SDE로 표현될 수 있음:
    (Eq. 8) $dX_{t}=\left( \frac{1}{2} \Sigma^{-1}(\mu-X_{t})-\nabla log \, p_{t}(X_{t})\right)\beta_{t}dt + \sqrt{\beta_{t}}d\tilde{W}_{t}, \,\,\, t\in [0,t]$
    - $\tilde{W}_{t}$ : reverse-time Brownian motion
    - $p_{t}$ : random variable $X_{t}$의 probability density function
    - 위의 SDE는 terminal condition $X_{T}$에서 시작하여 backward 방향으로 solve 됨
  • 이때 (Eq. 8) 대신 Ordinary Differential Equation (ODE)를 고려할 수 있음
    (Eq. 9) $dX_{t} = \frac{1}{2} \left( \Sigma^{-1}(\mu-X_{t})-\nabla log \, p_{t}(X_{t})\right)\beta_{t}dt$
    - 이때 (Eq. 2)와 (Eq. 9)에 해당하는 Kolmogorov equation은 동일하므로, (Eq. 2)와 (Eq. 9)를 따르는 stochastic process에서의 probability density function의 변화는 동일
  • 결과적으로 noisy data의 log-density gradient $\nabla log \, p_{t}(X_{t})$를 추정하는 neural network $s_{\theta}(X_{t},t)$가 있는 경우,
    - $\mathcal{N}(\mu, \Sigma)$에서 $X_{T}$를 sampling 하고,
    - (Eq. 8) 또는 (Eq. 9)를 backward solve 하여 data 분포 $Law(X_{0})$를 모델링 가능
    

- Loss Function

• Noisy data $X_{t}$에서 log-density gradient를 추정하는 것을 score matching이라고 함
  • 일반적으로 $L_{2}$ loss를 사용하여 gradient를 근사
  • (Eq. 6)으로 인해 intermediate value $\{ X_{s} \}_{s<t}$를 sampling 하지 않고도 initial data $X_{0}$만 주어지면 noisy data $X_{t}$를 생성할 수 있음
    - 이때 $Law(X_{t}|X_{0})$는 Gaussian이므로 log-density는 단순한 closed form을 가짐
  • $\mathcal{N}(0, \lambda(\Sigma, t))$에서 $\epsilon_{t}$를 sampling 하고 (Eq. 6)에 넣으면:
    (Eq. 10) $X_{t} = \rho (X_{0}, \Sigma, \mu, t)+\epsilon_{t}$
  • 이때 $X_{t}$에서의 log-density gradient는:
    (Eq. 11) $\nabla log \, p_{0t}(X_{t}|X_{0}) = -\lambda (\Sigma, t)^{-1}\epsilon_{t}$
    - $p_{0t}(\cdot | X_{0})$ : conditional 분포 (Eq. 6)의 probability density function
  • 결과적으로 time $t$ 동안 누적된 noise로 corrupte 된 data $X_{0}$의 log-density gradient를 추정하는 것에 대한 loss function은:
    (Eq. 12) $\mathcal{L}_{t}(X_{0})= \mathbb{E}_{\epsilon_{t}}\left[ || s_{\theta}(X_{t},t)+\lambda(\Sigma,t)^{-1}\epsilon_{t}||_{2}^{2}\right]$
    - $\epsilon_{t}$ : $\mathcal{N}(0, \lambda(\Sigma,t))$에서 sampling 되고, $X_{t}$는 (Eq. 10)에 따라 계산됨

3. Grad-TTS

• 제안하는 feature generator인 Grad-TTS는 encoder, duration predictor, decoder의 3가지 module로 구성됨

Overview of Grad-TTS

- Inference

• Grad-TTS는 length $L$을 가지는 input text sequence $x_{1:L}$로부터 mel-spectrogram $y_{1:F}$를 생성하는 것을 목표로 함 ($F$ : frame 수)
  • Encoder는,
    - Input text sequenc $x_{1:L}$을 duration predictor가 사용하는 feature sequence $\tilde{\mu}_{1:L}$로 변환하여
    - Encoded text sequence $\tilde{\mu}_{1:L}$와 frame-wise feature $\mu_{1:F}$ 사이의 hard monotonic alignment $A$를 생성
    - 이때 function $A$는 $[1, F] \bigcap \mathbb{N}$과 $[1,L] \bigcap \mathbb{N}$ 사이의 monotonic surjective mapping으로, 임의의 integer $j \in [1,F]$에 대해 $\mu_{j} = \tilde{\mu}_{A(j)}$
  • Duration predictor는
    - Text input의 각 element가 지속되는 frame 수를 알려주는 역할
    - $A$의 monotonicity와 surjectiveness는 text input을 skipping 하지 않고 correct order로 pronounce 되는 것을 보장함
    - 이때 예측된 duration에 대해 몇 가지 factor를 곱하여 합성된 음성의 tempo를 제어하는 것이 가능함
• Output sequence $\mu = \mu_{1:F}$는 decoder로 전달됨
  • Decoder는 Diffusion Probabilistic Model로써
    - 이때 parameter $\theta$가 있는 neural network $s_{\theta} (X_{t}, \mu, t)$는 아래의 Ordinary Differential Equation (ODE)를 정의:
    (Eq. 13) $dX_{t} = \frac{1}{2} (\mu-x_{t}-s_{\theta}(X_{t},\mu,t))\beta_{t}dt$
    - 이후 위 식을 first-order Euler scheme을 통해 time에 따라 backward로 solve
  • Sequence $\mu$는 terminal condition $X_{T} \sim \mathcal{N}(\mu,I)$를 정의하는 데 사용됨
    - Noise schedule $\beta_{t}$와 time horizon $T$는 data에 따라 달라지는 hyperparameter
    - Euler scheme의 step size $h$는 Grad-TTS가 학습된 이후에 선택할 수 있는 hyperparameter로 합성 품질과 추론 속도의 trade-off를 조절
• Grad-TTS의 reverse diffusion은 (Eq. 13)을 통해 전개됨
  1. (Eq. 8)보다 (Eq. 9)를 사용할 때 더 나은 결과를 얻을 수 있기 때문
     - Step size $h$가 작을 때는 비슷한 결과를 보이지만, 큰 size에 대해서는 (Eq. 9)가 더 나은 합성 품질을 보였음
  2. Feature generation pipeline을 단순화하기 위해 $\Sigma = I$를 사용
  3. Neural network $s_{\theta}(X_{t}, \mu, t)$에 대한 additional input으로 $\mu$를 활용
     - (Eq. 11)에서 neural network $s_{\theta}$는 noisy data $X_{t}$만을 사용하여 $X_{0}$에 추가된 Gaussian noise를 예측함
     - 따라서 매 time $t$ 마다 limiting noise $\displaystyle \lim_{T \to \infty} Law(X_{T}|X_{0})$에 대한 additional knowledge를 $s_{\theta}$에 제공하면 network는 time $t\in [0,T]$에서 더 정확하게 noise를 예측할 수 있음
     
• 추가적으로 Grad-TTS는 temperature hyperparameter $\tau$를 도입
  • $\mathcal{N}(\mu, I)$ 대신 $\mathcal{N}(\mu, \tau^{-1}I)$에서 terminal condition $X_{T}$를 sampling하는 것이 성능 향상에 유리
  • $\tau$를 조절함으로써 큰 step size $h$를 사용할 때 output mel-spectrogram의 품질을 유지할 수 있음

- Training

• Grad-TTS의 training objective는 aligned encoder output $\mu$와 target mel-spectrogram $y$ 사이의 거리를 최소화하는 것
  • 위에서 설명한 Grad-TTS의 추론이 random noise $\mathcal{N}(\mu, I)$에서 decoding이 시작되기 때문
    - 만약 target $y$에 가까운 noise에서 시작한다면 더 쉬운 decoding이 가능함
  • Aligned encoder output $\mu$가 decoder의 시작 noise를 parameterize 한다고 하면 encoder output $\tilde{\mu}$를 Normal 분포 $\mathcal{N}(\tilde{\mu}, I)$로 고려할 수 있고,
    - 이때 negative log-likelihood encoder loss는:
    (Eq. 14) $\mathcal{L}_{enc} = - \sum_{j=1}^{F} log \, \varphi(y_{j};\tilde{\mu}_{A(j)}, I)$
    - $\varphi (\cdot ; \tilde{\mu}_{i}, I)$ : $\mathcal{N}(\tilde{\mu}_{i}, I)$의 probability density function
    - Encoder loss $\mathcal{L}_{enc}$ 없이 학습시키는 것도 가능하지만, 이 경우 alignment를 학습하지 못하는 것으로 관찰됨
  • Encoder loss $\mathcal{L}_{enc}$는 encoder parameter와 alignment function $A$ 모두에 대해 최적화되어야 함
    - 이때 joint optimization을 수행하는 것은 어렵기 때문에, iterative approach를 활용
    
    1. Fixed encoder parameter가 주어지면 최적의 alignment $A^{*}$를 search
       - 이를 위해 Monotonic Alignment Search (MAS)를 도입
       - MAS는 loss function $\mathcal{L}_{enc}$의 관점에서 dynamic programming을 통해 monotonic surjective alignment를 찾음
    2. Alignment $A^{*}$를 fix 하고 stochastic gradient descent를 수행해 encoder parameter에 대한 loss function을 최적화
• 추론 시 최적의 alignment $A^{*}$를 추정하기 위해, Grad-TTS는 duration predictor network를 활용
  • Duration predictor $DP$는 log-domain에서 Mean Squared Error (MSE)를 통해 학습됨:
    (Eq. 15) $d_{i} = log \sum_{j=1}^{F}\mathbb{I}_{\{A^{*}(j)=i\}}, \,\,\, i=1, ..., L$
    $\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \mathcal{L}_{dp}=MSE(DP(sg[\tilde{\mu}]),d)$
    - $\mathbb{I}$ : indicator function
    - $\tilde{\mu} = \tilde{\mu}_{1:L}$, $d = d_{1:L}$
    - $sg[\cdot]$ : $\mathcal{L}_{dp}$가 encoder parameter에 영향을 주지 않도록 하는 stop gradient
  • DPM과 관련된 loss 계산 시, Grad-TTS는 $\Sigma =I$로 사용하므로 (Eq. 6)에 따른 noisy data의 분포를 단순화할 수 있고, covariance matrix는 scalar를 곱한 identity matrix $I$가 됨:
    (Eq. 16) $\lambda_{t} = 1- e^{-\int_{0}^{t}\beta_{s}ds}$
• 최종적인 diffusion loss function $\mathcal{L}_{diff}$는,
  • 서로 다른 time $t\in [0,T]$에서 noisy data의 log-density gradient를 추정하는 weighted loss에 대한 기댓값
    (Eq. 17) $\mathcal{L}_{diff} = \mathbb{E}_{X_{0},t} \left[ \lambda_{t}\mathbb{E}_{\xi_{t}} \left[ \left|\left| s_{\theta}(X_{t},\mu,t)+\frac{\xi_{t}}{\sqrt{\lambda_{t}}} \right|\right|_{2}^{2} \right]\right]$
    - $X_{0}$ : training data에서 sampling 된 target mel-spectrogram $y$
    - $t$는 uniform 분포 $[0,T]$에서 sampling 됨
    
  • $\xi_{t}$는 $\mathcal{N}(0,I)$ 및 (Eq. 6)에 따라 noisy data $X_{t}$를 얻는 데 사용되는 아래 식으로 sampling 됨:
    (Eq. 18) $X_{t} = \rho(X_{0},I,\mu,t)+\sqrt{\lambda_{t}}\xi_{t}$
  • (Eq. 17)과 (Eq. 18)에서 $\epsilon_{t} = \sqrt{\lambda_{t}}\xi_{t}$로 치환하면 (Eq. 12)와 (Eq. 10)을 따름
    - 이때 (Eq. 12)에 대해 $1/\mathbb{E}\left[ || \nabla log \, p_{0t}(X_{t}|X_{0}) ||_{2}^{2} \right]$에 비례하는 weight $\lambda_{t}$를 적용
    
• 결론적으로 training procedure는 아래와 같이 진행됨
  1. Encoder, duration predictor, decoder의 parameter를 fix 하고, MAS를 통해 $\mathcal{L}_{enc}$를 최소화하는 alignment $A^{*}$를 search
  2. Alignment $A^{*}$를 fix하고, encoder, duration predictor, decoder의 parameter에 대해 $\mathcal{L}_{enc}+\mathcal{L}_{dp}+\mathcal{L}_{diff}$를 최소화
  3. 위 과정을 수렴할 때까지 반복

- Model Architecture

• Encoder와 Duration predictor는 Glow-TTS와 동일한 architecture를 사용
  • Duration predictor는 2개의 convolution layer와 log duration을 예측한 projection layer로 구성됨
  • Encoder는 pre-net, 6개의 transformer block, linear projection layer로 구성됨
    - Pre-net은 3개의 convolution layer와 fully-connected layer로 구성됨
• Decoder network $s_{\theta}$는 U-Net architecture를 활용
  • 이때 model size를 줄이기 위해 2배 더 적은 channel과 3개의 feature map resolution을 활용
  • 80-dimensional mel-spectrogram을 사용한다고 했을 때, $s_{\theta}$는 $80 \times F$, $40 \times F/2$, $20 \times F/4$ resolution에서 동작
    - Frame 수 $F$가 4의 배수가 아닌 경우, mel-spectrogram을 zero-padding
    - Aligned encoder output $\mu$는 U-Net input $X_{t}$와 concatenate 됨

Diffusion Loss 그래프

4. Experiments

- Settings

• Dataset : LJSpeech
• Comparisons : FastSpeech, Glow-TTS, Tacotron2

- Result

• Subjective Evaluation
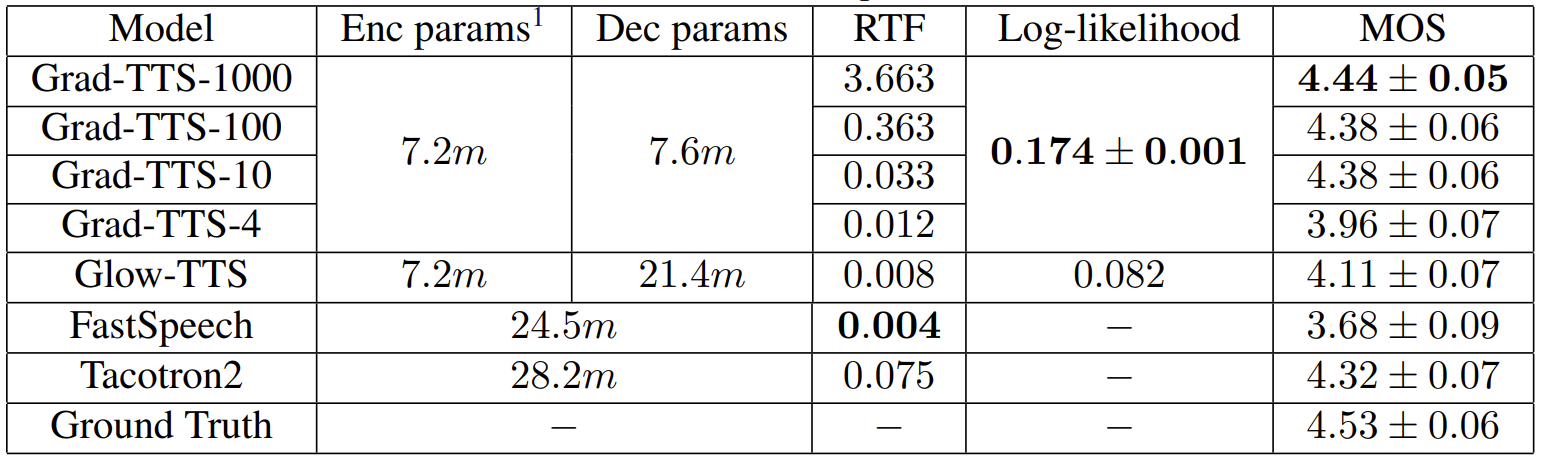
  • MOS 측면에서 합성 품질을 비교해 보면, reverse diffusion을 많이 반복할수록 Grad-TTS의 합성 품질이 좋아짐
    - 대신 특정 반복 이상부터는 품질 향상이 미미함
  • FastSpeech 등의 다른 모델들과 비교했을 때도 Grad-TTS가 가장 우수한 품질을 달성
• Objective Evaluation
  • Grad-TTS는 Glow-TTS 보다 더 나은 log-likelihood를 보임
  • 특히 parameter 측면에서 Grad-TTS는 Glow-TTS 보다 3배 더 적은 decoder만으로도 더 우수한 성능을 달성

합성 품질 비교

• Generalized DPM framework의 효과를 확인하기 위해 $\mathcal{N}(\mu, I)$ 대신 $\mathcal{N}(0,I)$에서의 mel-spectrogram reconstruction을 비교
  • $\mathcal{N}(0,I)$에서 모델을 10, 20, 50번 반복하는 것보다 $\mathcal{N}(\mu,I)$를 사용하는 기존의 Grad-TTS가 더 선호되는 것으로 나타남
  • $\mathcal{N}(0,I)$에서 reconstruction을 수행할 때, 기존 Grad-TTS 보다 더 많은 ODE-solver step이 필요하다는 것을 의미

선호도 비교

• 각 TTS 모델에서 발생하는 error의 종류에 대한 테스트를 수행
  • Glow-TTS의 경우 단어를 잘못된 방식으로 stress 하는 경우와 robotic 한 음성을 생성하는 경우가 많은 것으로 나타남
  • 그에 비해 Grad-TTS는 Glow-TTS, Tacotron2 보다 더 적은 error를 발생시킴

Error 발생 비교

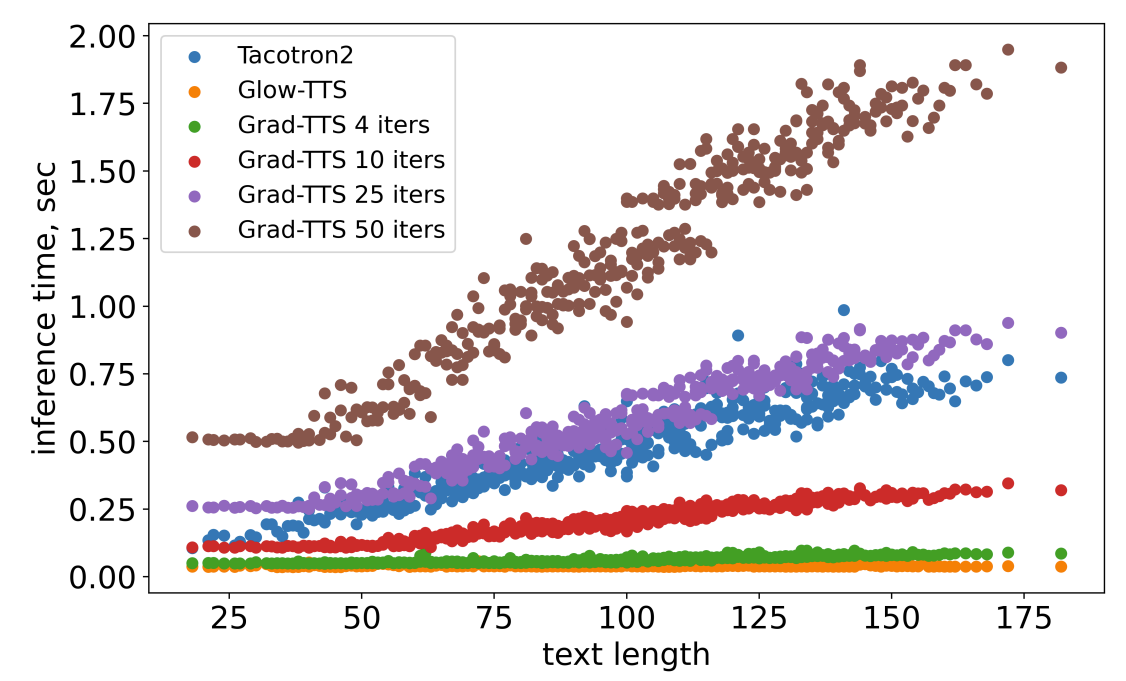
- Efficiency Estimation

• Grad-TTS는 decoder step이 100 이하인 경우 0.37보다 작은 RTF를 달성 가능
  • 추론 속도 측면에서는 Glow-TTS, FastSpeech2보다 다소 느리지만 Tacotron2보다는 빠른 속도를 보임
  • 특히 Grad-TTS는 약 15M의 parameter를 가지므로 model size 측면에서는 가장 효율적임

추론 속도 비교