[Paper 리뷰] VoiceFlow: Efficient Text-to-Speech with Rectified Flow Matching

VoiceFlow: Efficient Text-to-Speech with Rectified Flow Matching

---

• Text-to-Speech에서 diffusion model은 우수한 성능을 보이고 있지만 sampling complexity로 인해 비효율적임
• VoiceFlow
  • 제한된 sampling step으로도 고품질의 합성을 수행할 수 있는 rectified flow matching을 활용
  • Text input을 condition으로 하여 mel-spectrogram을 ordinary differential equation을 통해 추정
  • Rectified flow는 효율적인 합성을 위해 sampling trajectory를 straighten 함
• 논문 (ICASSP 2024) : Paper Link

---

1. Introduction

• Text-to-Speech에서 Grad-TTS, DiffVoice와 같은 diffusion-based TTS 모델은 우수한 합성 품질을 보이고 있음
  • 이러한 diffusion model은 Stochastic Differential Equation (SDE)의 score function $\nabla \log p_{t}(x)$를 추정하는 방식으로 stable 하게 train 됨
    - 이후 reverse-time SDE나 probability-flow Ordinary Differential Equation (ODE)를 numerically solving 하여 sample을 생성함
  • BUT, diffusion model은 우수한 성능에도 불구하고 efficiency의 문제가 있음
    1. SDE/ODE sampling은 만족스러운 sample을 얻기 위해 상당한 step이 필요하므로 latency 증가로 이어짐
    2. 이러한 diffusion TTS 모델의 speed-quality tradeoff를 개선하기 위해 여러 방법들이 도입되었음
       - BDDM의 diffusion noise schedule을 활용해 최적화하거나, Distillation technique을 적용하는 방법
       - LightGrad의 경우 probability-flow ODE의 solution을 explicitly derive 하기 위해 DPM-Solver를 채택
    3. 앞선 방식들은 diffusion model의 sampling step을 어느 정도 줄이긴 했지만, diffusion process의 근본적인 특성으로 인해 speed-quality tradeoff는 여전히 존재함
  • 한편으로 denoising diffusion 외에 differential equation을 사용하는 또 다른 생성 모델인 flow matching model을 고려할 수 있음
    - Diffusion model은 특정 SDE의 score function을 학습하지만, flow matching은 arbitrary ODE로 imply 된 vector field를 직접 모델링함
    - 이때 vector field를 근사하기 위해 neural network를 적용하고 ODE를 numerically solve 하여 data sample을 얻음
  • ODE, vector field 설계에서는 sampling trajectory를 linearizing 하고 transport cost를 최소화하는 것을 목표로 함
    - 결과적으로 flow matching model은 더 간단한 formulation과 더 적은 constraint를 가지면서도 높은 품질을 얻을 수 있고, 특히 rectified flow는 ODE trajectory를 더 straighten 할 수 있음

-> 그래서 TTS acoustic model에 rectified flow matching을 적용한 VoiceFlow를 제안

 

• VoiceFlow
  • Noise 분포와 mel-spectrogram 사이의 flow에 대한 ODE를 구성하고 phone과 duration을 사용하여 conditioning 함
  • 이때 estimator는 vector field 하에서 모델링하는 방법을 학습하고, flow rectification process를 통해 trained flow matching model에서 sample을 생성한 다음, 다시 train 함
  • 이를 통해 훨씬 적은 step만으로도 적절한 mel-spectrogram을 생성할 수 있음

< Overall of VoiceFlow >

• Rectified flow matching을 활용해 text input을 condition으로 하는 mel-spectrogram을 ODE로 추정
• Rectified flow는 효율적인 합성을 위해 sampling trajectory를 straighten 함
• 결과적으로 적은 step 수에서도 품질을 유지하고, 기존 diffusion model 보다 더 뛰어난 speed-quality tradeoff를 달성

2. Flow Matching and Rectified Flow

- Flow Matching Generative Models

• Data 분포를 $p_{1}(x_{1})$이라고 하고 tractable prior 분포를 $p_{0}(x_{0})$라고 하자
  • 대부분의 생성 모델은 sample $x_{0}\sim p_{0}(x_{0})$를 data $x_{1}$에 mapping 하는 방법을 찾는 방식으로 동작함
    - 특히 diffusion model은 SDE를 구성한 다음, 이를 통해 얻어진 probability path $p_{t}(x_{t})$의 score function을 추정함
    - Sampling은 해당 probability path와 함께 reverse-time SDE나 probability-flow ODE를 solve 하는 것으로 수행됨
  • Flow matching model은 probability path $p_{t}(x_{t})$를 직접 모델링하는 방법으로써,
    1. 다음의 arbitrary ODE가 있다고 하면:
       (Eq. 1) $\mathrm{d}x_{t}=v_{t}(x_{t})\mathrm{d}t$
       - $v_{t}(\cdot)$ : $t\in [0,1]$에서 vector field
    2. 해당 ODE는 continuity equation $\frac{\mathrm{d}}{\mathrm{d}t}\log p_{t}(x)+\mathrm{div}(p_{t}(x)v_{t}(x))=0$에 의해 probability path $p_{t}(x_{t})$와 연관됨
    3. 이때 neural network가 vector field $v_{t}(\cdot)$을 정확하게 추정할 수 있다면, realistic data를 충분히 얻을 수 있음
       - (Eq. 1)의 ODE는 neumerically solve 가능하기 때문 
  • Vector field의 설계는 practically apply 되기 전에 instantiate 되어야 하고, 이때 data sample $x_{1}$을 사용하여 conditional probability path를 구성하는 방법은 다음과 같이 제시됨
    1. 먼저 충분히 작은 $\sigma$에 대해 boundary condition $p_{t=0}(x|x_{1})=p_{0}(x)$와 $p_{t=1}(x|x_{1})=\mathcal{N}(x|x_{1},\sigma^{2}I)$에 대한 probability path가 $p_{t}(x|x_{1})$이라고 하자
       - 그러면 continuity equation을 따라 associated vector field $v_{t}(x|x_{1})$이 존재함
    2. 여기서 neural network $u_{\theta}$에 의한 conditional vector field 추정은, expectation 측면에서 unconditional vector field를 추정하는 것과 동치라는 것이 증명되어 있음:
       (Eq. 2) $\min_{\theta}\mathbb{E}_{t,p_{t}(x)}|| u_{\theta}(x,t)-v_{t}(x)||^{2}$
       (Eq. 3) $\equiv \min_{\theta}\mathbb{E}_{t,p_{1}(x_{1}),p_{t}(x|x_{1})}||u_{\theta}(x,t)-v_{t}(x|x_{1})||^{2}$
    3. 이후 간단한 conditional probability path $p_{t}(x|x_{1})$과 해당 $v_{t}(x|x_{1})$을 설계함으로써 $p_{t}(x|x_{1})$에서 sample을 추출하고 (Eq. 3)을 최소화함
       - e.g.) Gaussian path $p_{t}(x|x_{1})=\mathcal{N}(x|\mu_{t}(x_{1}),\sigma_{t}(x_{1})^{2}I)$와 linear vector field $v_{t}(x|x_{1})=\frac{\sigma'_{t}(x_{1})}{\sigma_{t}(x_{1})}(x-\mu_{t}(x_{1}))+\mu'_{t}(x_{1})$를 사용할 수 있음
  • 한편으로 해당 conditioning을 generalize 하여, $p_{t}(x|z)$에 대한 any condition $z$는 (Eq. 3)과 동일한 형태의 optimization target으로 구성될 수 있음
    - 이때 probability path $p_{t}(x|x_{0},x_{1})=\mathcal{N}(x|tx_{1}+(1-t)x_{0},\sigma^{2}I)$를 구성하는 noise sample $x_{0}$에 대한 additional condition을 활용
  • 결과적으로 conditional vector field는 $v_{t}(x|x_{0},x_{1})=x_{1}-x_{0}$가 되고, $x_{1}$에 대한 constant straight line으로 나타나므로, 해당 formulation에서는 다음의 과정으로 생성 모델을 training 함
    1. Data에서 $x_{1}$을 sampling 하고, noise 분포 $p_{0}(x_{0})$에서 $x_{0}$를 sampling힘
    2. Time $t\in[0,1]$을 sampling 하고, $x_{t}\sim \mathcal{N}(tx_{1}+(1-t)x_{0}, \sigma^{2}I)$를 sampling 함
    3. Loss $|| u_{\theta}(x,t)-(x_{1}-x_{0})||^{2}$에 graident descent를 적용함
       - 이를 conditional flow matching이라고 하고, diffusion model보다 더 나은 성능을 보이는 것으로 알려짐

- Improved Sampling Efficiency with Rectified Flow

• Rectified flow는 flow matching model의 sampling efficiency를 향상하기 위해 제안됨
  • 먼저 flow matching model이 (Eq. 1)의 ODE에 의해 noise $x_{0}$에서 data $\hat{x}_{1}$를 생성하도록 train 되었다고 하자
    1. 즉, $x_{0}$와 $\hat{x}_{1}$은 ODE trajectory의 starting, ending point의 pair로 볼 수 있음
    2. 그러면 해당 flow matching model은 다시 한번 train 되면서 $x_{0}, x_{1}$을 independently sampling 하는 대신, 주어진 pair $(x_{0}, \hat{x}_{1})$에 대해 $v_{t}(x|x_{0},x_{1}), p_{t}(x|x_{0},x_{1})$ condition을 적용함
    3. 해당 flow rectification step은 여러 번 iteration 되어, 재귀로써 $\left(z_{0}^{k+1},z_{1}^{k+1}\right)=\mathrm{FM}(z_{0}^{k},z_{1}^{k})$로 나타낼 수 있음
       - $\mathrm{FM}$ : flow matching model, $(z_{0}^{0},z_{1}^{0}) = (x_{0},x_{1})$ : independently draw 된 noise, data sample
  • 직관적으로 rectified flow는 flow matching model의 sampling trajectory를 rewire 하여 straight 하게 만듦
    - ODE trajectory는 solve 될 때 intersect 될 수 없기 때문에, trajectory는 training의 conditional vector field만큼 straight 하지 않을 수 있음
    - BUT, 동일한 trajectory의 endpoint에서 flow matching model을 다시 training 함으로써, 모델은 noise와 data를 연결하는 더 짧은 path를 학습할 수 있음
  • 이러한 rectified flow의 straightening tendency는 이론적으로 보장되어 있으므로, 결과적으로 trajectory rectifying을 통해 flow matching model은 더 적은 수의 ODE step만으로도 data를 효율적으로 sampling 할 수 있음

3. VoiceFlow

- Flow Matching-based Acoustic Model

• TTS에서 flow matching model을 활용하기 위해, 논문은 mel-spectrogram $x_{1}\in \mathbb{R}^{d}$를 target data로 하고, standard Gaussian $\mathcal{N}(0,I)$의 noise $x_{0}\in \mathbb{R}^{d}$를 사용하여 non-autoregressive conditional generation 문제로 casting 함
  • 먼저 VoiceFlow는 DiffSinger와 같이 forced alignment로부터 duration learning module을 사용함
    - Duplicated latent phone representation을 $y$라 했을 때, 각 phone의 latent embedding은 duration에 따라 repeat 되고 $y$는 generation process의 condition으로 볼 수 있음
  • $v_{t}(x_{t}|y) \in \mathbb{R}^{d}$가 ODE $\mathrm{d}x_{t}=v_{t}(x_{t}|y)\mathrm{d}t$에 대한 underlying vector field라고 하자
    1. 해당 ODE는 text $p_{1}(x_{1}|y)=p_{mel}(x_{1}|y)$에 대해 noise 분포 $p_{0}(x_{0}|y)=\mathcal{N}(0,I)$를 mel-distribution과 연결함
    2. 이때 VoiceFlow의 목표는 주어진 condition $y$에 대해 vector field $v_{t}$를 추정하는 것이고, $t=0$에서 $t=1$까지 해당 ODE를 solve 하여 mel-spectrogram을 생성할 수 있음
       
  • 결과적으로 VoiceFlow는 noise sample $x_{0}$와 data sample $x_{1}$을 모두 사용하여,
    1. Conditional probability path를 다음과 같이 구성함:
       (Eq. 4) $p_{t}(x|x_{0},x_{1},y)=\mathcal{N}(x|tx_{1}+(1-t)x_{0},\sigma^{2}I)$
       - $\sigma$ : 충분히 작은 constant
       - 위 식에서 path의 endpoint는 $t=0$인 경우, $\mathcal{N}(x_{0},\sigma^{2}I)$이고 $t=1$인 경우, $\mathcal{N}(x_{1},\sigma^{2}I)$
    2. 해당 path는 $x_{0}, x_{1}$에 대해 boundary가 noise 분포 $p_{0}(x_{0}|y)$, mel-distribution $p_{1}(x_{1}|y)$에 가까운 probability path $p(x|y)$를 결정함
       - 직관적으로 (Eq. 4)는 linear path로 이동하는 Gaussian family를 나타내고, 관련된 vector field 역시 $v_{t}(x|x_{0},x_{1},y)=x_{1}-x_{0}$로써, constant linear line으로 나타남
    3. 이후 neural network $u_{\theta}$를 사용하여 vector field를 추정하고, 해당 objective는 (Eq. 3)과 유사하게:
       (Eq. 5) $\min_{\theta}\mathbb{E}_{t,p_{1}(x_{1},y),p_{0}(x_{0}|y),p_{t}(x_{t}|x_{0},x_{1},y)}||u_{\theta}(x_{t},y,t)-(x_{1}-x_{0})||^{2}$
    4. 여기서 flow matching loss를 $\mathcal{L}_{FM}$, duration predictor의 loss를 $\mathcal{L}_{dur}$이라고 했을 때, VoiceFlow의 total loss function은 $\mathcal{L}=\mathcal{L}_{FM}+\mathcal{L}_{dur}$
  • 구조적으로 VoiceFlow의 acoustic model은 아래 그림과 같이 text encoder, duration predictor, duration adaptor, vector field estimator로 구성됨
    
    1. Text encoder는 input phone을 latent space로 변환하고, 이때 phone에 대한 duration이 예측되고 duration adaptor에 제공됨
    2. Repeated frame-level sequence $y$는 condition으로써 vector field estimator에 제공됨
       - Vector field estimator에 대한 2개의 input은 sampled time $t$와 (Eq. 4)의 conditional probability path에서 sampling 된 $x_{t}$
    3. VoiceFlow는 Grad-TTS와 같이 vector field estimator에 대해 U-Net architecture를 채택함
       - 결과적으로 condition $y$는 estimator에 제공되기 전에 $x_{t}$와 concatenate 되고 time $t$는 각 residual block의 hidden variable에 추가되기 전에 fully connected layer를 통과함

Overall of VoiceFlow

- Sampling and Flow Rectification Step

• (Eq. 5)에 의해 vector field estimator $u_{\theta}$는 expectation 측면에서 $v_{t}$를 근사할 수 있음
  • ODE $\mathrm{d}x_{t}=u_{\theta}(x_{t}, y,t)\mathrm{d}t$는 주어진 text $y$에 대해 synthetic mel-spectrogram $x_{1}$을 sampling 하기 위해 discretize 됨
    - 여기서 Euler, Runge-Kutta, Dormand-Prince method와 같은 ODE solver를 sampling에 적용할 수 있음
  • $N$ step Euler method의 경우, 각 sampling step은:
    (Eq. 6) $\hat{x}_{\frac{k+1}{N}}=\hat{x}_{\frac{k}{N}}+\frac{1}{N}u_{\theta}\left(\hat{x}_{\frac{k}{N}},y,\frac{k}{N}\right), \,\, k=0,1,...,N-1$
    - $\hat{x}_{0}\sim p_{0}(x_{0}|y)$ : initial point, $\hat{x}_{1}$ : 생성된 sample
    - Discretization method에 관계없이, solver는 ODE trajectory를 따라 점진적으로 realistic spectrogram에 가까워지는 일련의 sample $\{\hat{x}_{k/N}\}$을 생성함
  • 이후 rectified flow를 적용하여 ODE trajectory를 straighten 함
    1. 먼저 training set의 모든 utterance에 대해 noise sample $x'_{0}$를 얻고 ODE solver를 통해 주어진 text $y$에 대한 $\hat{x}_{1}$을 얻음
    2. Sample pair $(x'_{0}, \hat{x}_{1})$은 vector field estimator를 rectifying 하기 위해 VoiceFlow에 다시 공급됨
    3. 이러한 rectification step에 대한 training criterion은:
       (Eq. 7) $\min_{\theta}\mathbb{E}_{t,p(x'_{0},\hat{x}_{1}|y),p_{t}(x_{t}|x'_{0},\hat{x}_{1},y)}||u_{\theta}(x_{t},y,t)-(\hat{x}_{1}-x'_{0})||^{2}$
       - 위 식과 (Eq. 5)와의 차이점은 independently sampling 하지 않고 pair $(x'_{0},\hat{x}_{1})$을 사용한다는 것
       - 즉, (Eq. 7)에서 모든 spectrogram sample $\hat{x}_{1}$은 동일한 trajectory의 noise sample과 연관됨
  • 위 방식을 통해 vector field estimator는 $(x'_{0}, \hat{x}_{1})$을 연결하는 보다 간단한 sampling trajectory를 찾게 되고, 결과적으로 sampling efficiency를 향상할 수 있음
    - 이때 rectified flow에 대한 data를 생성하는 동안 ground-truth duration sequence를 모델에 제공함
    - 이를 통해 모델에 natural speech를 제공하여 inaccurate duration으로 인한 성능 저하를 방지함

VoiceFlow Training Algorithm

4. Experiments

- Settings

• Dataset : LJSpeech, LibriTTS 
• Comparisons : Grad-TTS

- Results

• Subjective Evaluations
  • MOS 측면에서 VoiceFlow는 Grad-TTS 보다 우수한 품질을 보임
  • 특히 sampling step이 줄어들면 Grad-TTS의 품질은 크게 저하되지만 VoiceFlow는 큰 저하가 나타나지 않음

MOS 비교 결과

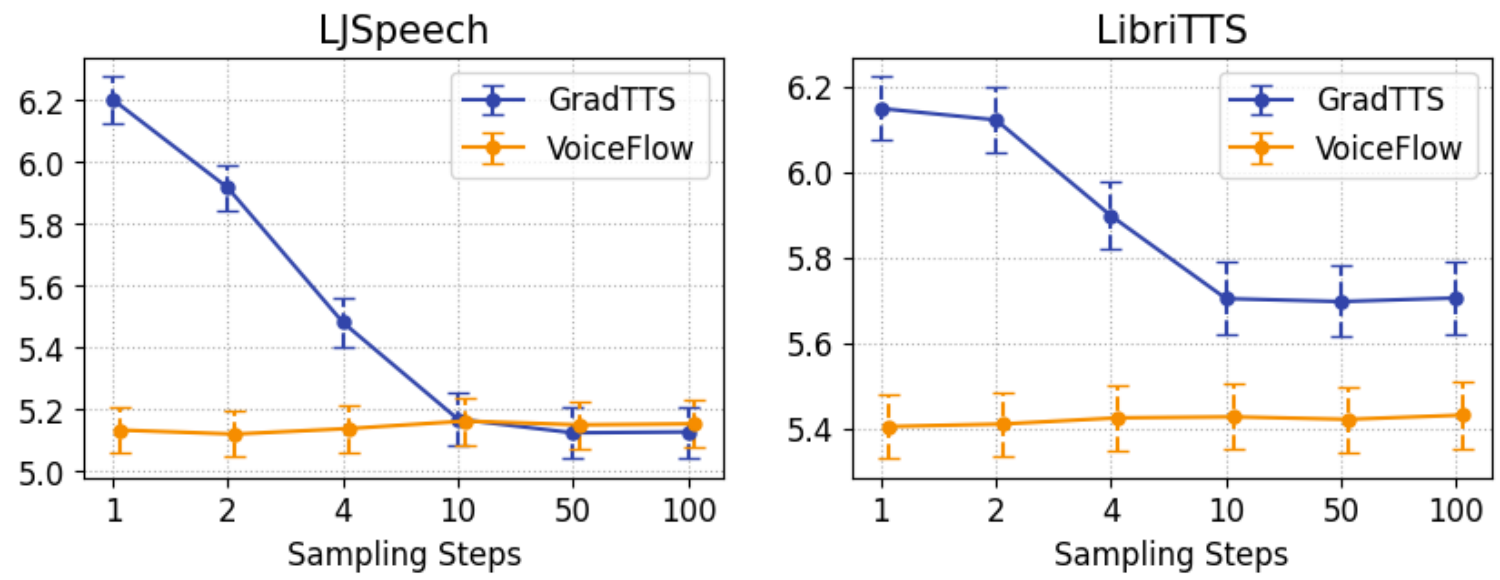
• Objective Evaluations
  • MOSNet과 Mel-Cepstral Distortion (MCD) 측면에서 VoiceFlow의 성능을 비교해 보면
  • 다양한 sampling step에 대해 VoiceFlow의 성능 변화는 Grad-TTS 보다 낮게 나타남
    - 결과적으로 VoiceFlow는 diffusion model 보다 더 나은 speed-quality tradeoff를 달성할 수 있음

Sampling Step 별 MOSNet의 결과

Sampling Step 별 MCD 변화

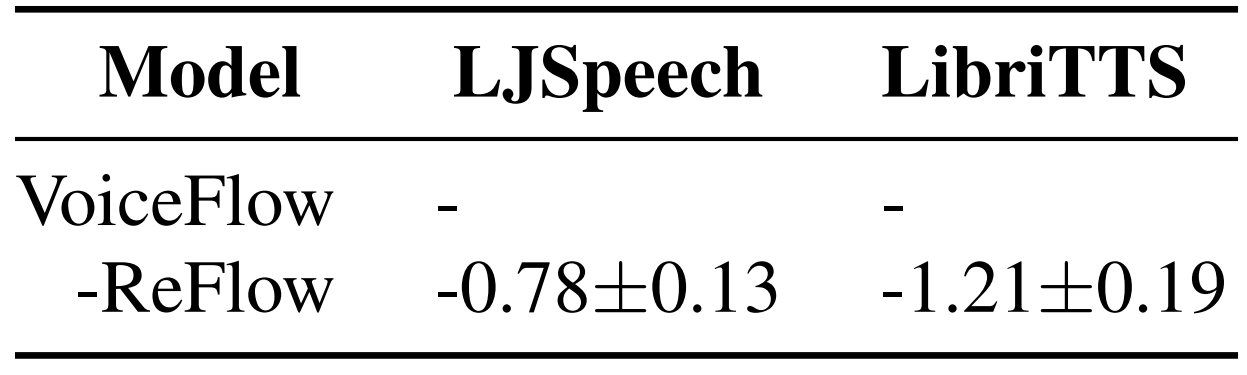
• Ablation Study
  • Rectified flow를 제거하는 경우 VoiceFlow의 성능은 저하되는 것으로 나타남
  • 추가적으로 sampling trajectory를 확인해 보면, VoiceFlow는 Grad-TTS에 비해 더 straight 한 trajectory를 나타냄

Ablation Study 결과

Sampling Trajectory 비교