[Paper 리뷰] DiffSinger: Singing Voice Synthesis via Shallow Diffusion Mechanism

DiffSinger: Singing Voice Synthesis via Shallow Diffusion Mechanism

---

• Singing Voice Synthesis (SVS)는 음향 feature 재구성을 위해 간단한 Loss나 GAN을 활용함
• 각각의 방식은 over-smoothing 문제와 불안정한 학습과정으로 인해 부자연스러운 음성을 만들어냄
• DiffSinger
  • Diffusion probabilistic 모델 기반의 SVS용 음향 모델
  • 조건부 분포 하에서 노이즈를 mel-spectrogram으로 반복적으로 변환하는 parameterized Markov chain
  • Variational bound를 최적화함으로써 안정적이고 자연스러운 음성을 합성
• 논문 (AAAI 2022) : Paper Link

---

1. Introduction

• SVS는 자연스러운 가창 음성을 합성하는 것을 목표로 함
  • 악보에 따라서 음향 특징을 생성하는 음향 모델과 음향 특징을 waveform으로 변환하는 vocoder로 구성
  • 기존의 SVS 모델은 단순한 Loss (L1, L2 Loss)를 활용해서 음향 특징을 재구성함
    - Unimodal distribution assumption을 기반으로 하므로 over-smoothing 현상이 발생
  • Generative Adversarial Network (GAN)을 활용할 수도 있음
    - Discriminator가 불안정하므로 학습시키기 어려움

• 유연한 생성 모델인 diffusion probabilistic 모델이 등장
  • Diffusion process와 Reverse (denoising) process 두 과정으로 구성
    - Diffusion process : fixed parameter가 있는 Markov chain에서 점진적으로 Gaussian noise를 추가하여 복잡한 data를 isotropic Gaussian distribution으로 변환하는 것
    - Reverse process : 반복적으로 Gaussian noise에서 original data를 복원하는 Markov chain
  • Data likelihood에 대한 variational lower bound (ELBO)를 최적화하여 diffusion 모델을 학습

-> 그래서 안정적인 학습과 자연스러운 보컬 합성을 위해  diffusion 기반의 SVS용 음향 모델인 DiffSinger를 제안

 

• DiffSinger
  • Adversarial feedback 없이 ELBO를 최적화하여 ground-truth 분포와 일치하는 사실적인 mel-spectrogram을 생성하는 diffusion 모델
  • 음성 품질을 개선하고, prior knowledge를 더 활용하기 위해 shallow diffusion mechanism을 도입
  • Diffusion step이 충분히 클 때, ground-truth mel-spectrogram $M$과 decoder $\tilde{M}$에 의해 예측된 diffusion trajectory에 intersection이 존재함
    
    - 추론단계에서:
    1. Mel-spectrogram decoder를 활용해 $\tilde{M}$을 생성
    2. Diffusion process를 통해 shallow step $k$에서 sample을 계산하여 $\tilde{M}_{k}$를 얻음
    3. Gaussian noise가 아닌 $\tilde{M}_{k}$에서 reverse process 수행
    - Boundary predcition network를 학습시켜 intersection을 찾고 적응적으로 $k$를 결정
  • Shallow diffusion mechanism은 Gaussian noise 보다  더 나은 시작점을 제공하여 reverse process에서 합성된 오디오 품질을 향상시킴

< Overall of DiffSinger >

• Diffusion probabilistic 모델을 기반으로 하는 SVS용 음향 모델
• 합성 품질을 향상하기 위한 shallow diffusion mechanism 도입
• TTS 작업으로의 일반화 가능성 제시

2. Diffusion Model

- Diffusion Process

• Diffusion probabilistic 모델 : raw data를 diffsuion process를 통해 점진적으로 Gaussian 분포로 변환한 다음, reverse process를 학습하여 Gaussian noise로부터 data를 복원하는 모델
• Diffusion process : fixed parameter가 있는 Markov chain으로, $T$ step에서 $y_{0}$를 latent $y_{T}$로 변환
  - Data 분포 : $q(y_{0})$, Sample : $y_{0} \sim q(y_{0})$

Diffusion process 유도 1

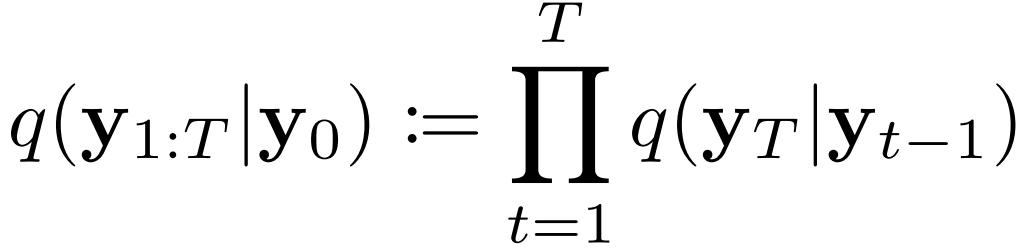
• 각 diffusion step $t \in [1, T]$에서, tiny Gaussian noise가 variance schedule $\beta = \{\beta_{1}, ..., \beta_{T} \}$에 따라 $y_{t}$를 얻기 위해 $y_{t-1}$에 더해짐

Diffusion process 유도 2

• $\beta$가 잘 설계되고 $T$가 충분히 크면, $q(y_{T})$는 거의 isotropic Gaussian 분포를 따름
  - $q(y_{t}|y_{0})$가 $O(1)$ 시간 내에 closed form으로 계산될 수 있는 속성을 가짐
  - $\bar{\alpha}_{t} := \prod^{t}_{s=1} \alpha_{s}, \alpha_{t} := 1-\beta_{t}$

Diffusion process 유도 3

- Reverse Process

• Reverse process : $y_{T}$에서 $y_{0}$까지 learnable parameter $\theta$가 있는 Markov chain
  - 정확한 reverse transition 분포 $q(y_{t-1})$은 intractable 하므로, 매 $t$-th step에서 공유되는 parameter $\theta$를 활용해 neural network로 approximation

Reverse process 유도 1

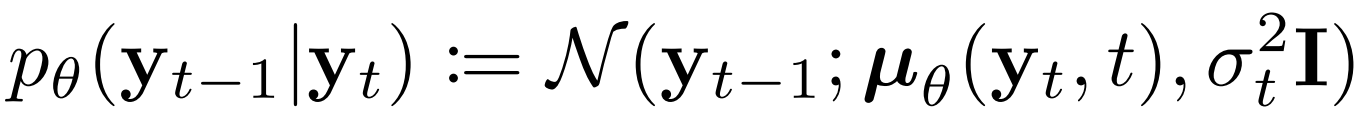
• 이때 전체 reverse process는 아래와 같이 정의됨

Reverse process 유도 2

- Training

• Parameter $\theta$를 학습하기 위해서 negative loglikelihood의 variational bound를 최소화해야 함

Training 과정 유도 1

• 효율적인 학습 방식은 stochastic gradient descent로 $L$의 random term을 최적화하는 것
  - $q(y_{t-1}|y_{t}, y_{0}) = N(y_{t-1}; \tilde{\mu}_{t}(y_{t}, y_{0}), \tilde{\beta}_{t}I)$
  - $\tilde{\mu}_{t}(y_{t}, y_{0}) := \frac{\sqrt{\bar{\alpha}_{t-1}}\beta_{t}}{1-\bar{\alpha}_{t}}y_{0} + \frac{\sqrt{\alpha_{t}}(1-\bar{\alpha}_{t-1})}{1-\bar{\alpha}_{t}}y_{t}$
  - $\tilde{\beta}_{t} := \frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_{t}}\beta_{t}$

Training 과정 유도 2

• 이때 위 식은 아래와 동치
  - $C$ : 상수

Training 과정 유도 3

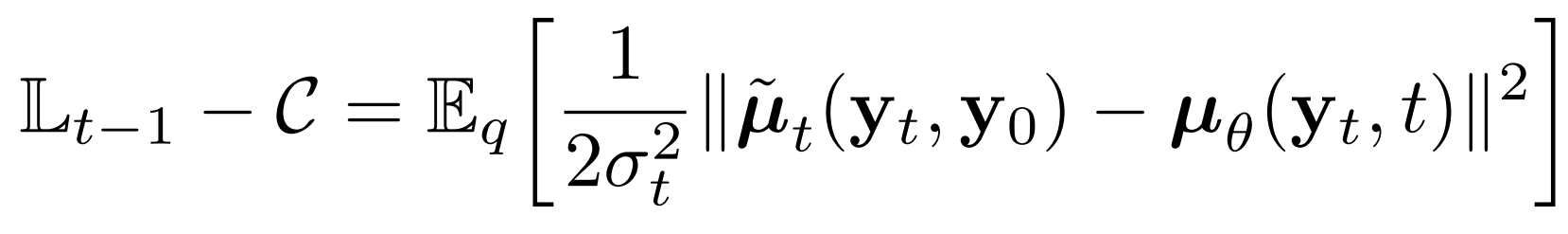
• $y_{t}(y_{0}, \epsilon) = \sqrt{\bar{\alpha}_{t}} y_{0} + \sqrt{1 - \bar{\alpha}_{t}} \epsilon$으로 diffusion process를 reparameterizing 하면,

Training 과정 유도 4

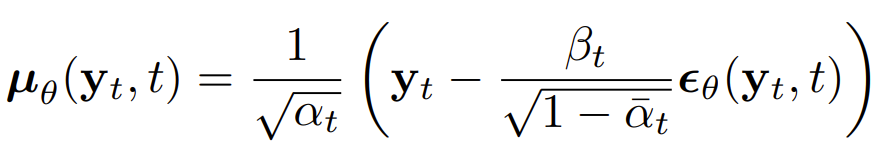
• 위 식을 간단히 하면,
  - $\sigma^{2}_{t}$를 $\tilde{\beta}_{t}$로 두고, sample $\epsilon \sim N(0, I)$를 얻음
  - $\epsilon_{\theta}(\cdot)$ : neural network의 output

Training 과정 유도 5

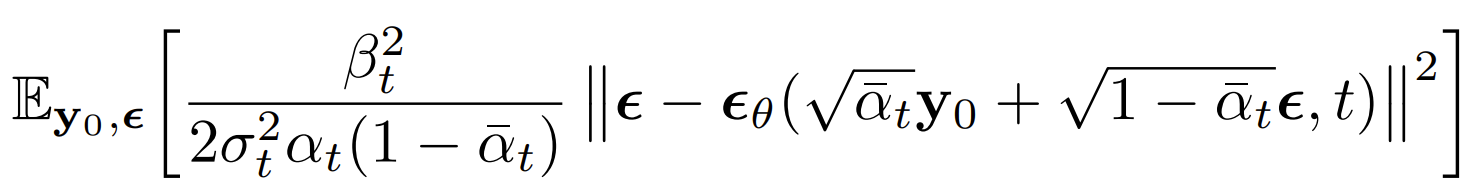
- Sampling

• $p(y_{T}) \sim N(0, I)$에서 $y_{T}$를 sampling 하고, 얻어진 data sample로부터 reverse process를 수행 

Diffusion model의 일반적인 구조

3. DiffSinger

• DiffSinger는 diffusion 모델을 기반으로 함
• SVS 작업은 조건부 분포 $p_{\theta}(M_{0}|x)$를 모델링해야 하므로, $x$를 reverse process에서 조건으로 diffusion denoiser에 추가함
  - $M$은 mel-spectrogram, $x$는 $M$에 해당하는 악보

DiffSinger의 전체 구조

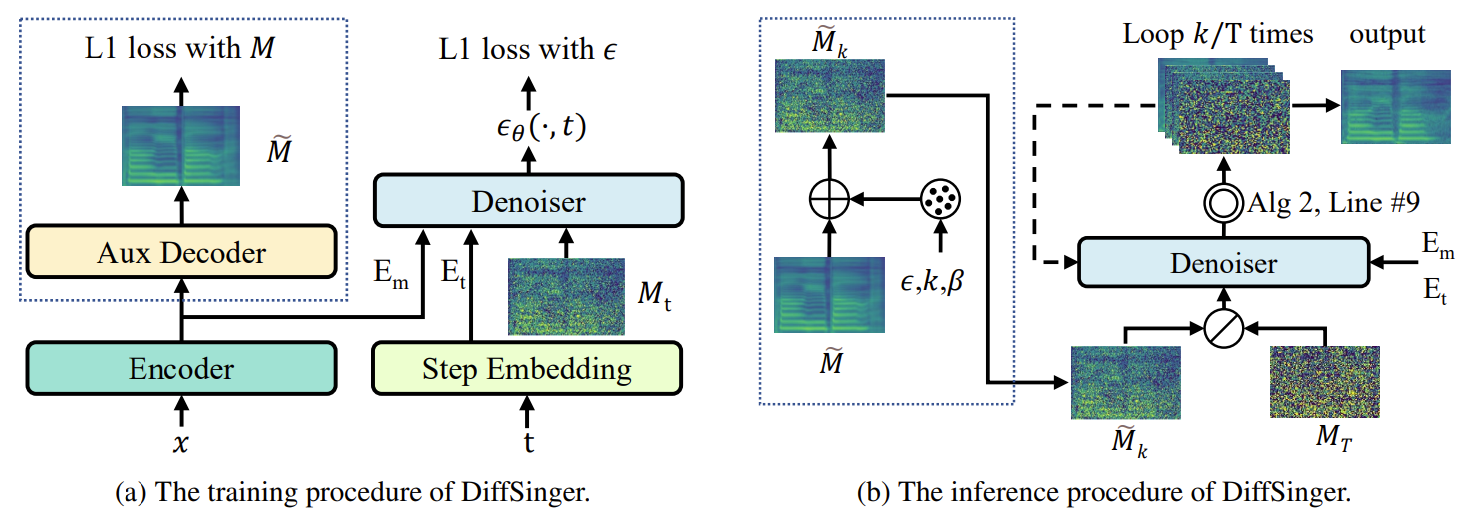
- Naive Version of DiffSinger

• Training 단계
  • Naive DiffSinger는 diffusion process의 $t$-th step mel-spectrogram $M_{t}$에서 random noise $\epsilon_{\theta}(\cdot)$을 예측함
  • $t$와 악보 $x$를 조건으로 함

DiffSinger의 Training 과정

• Inference 단계
  • $N(0, I)$에서 sampling 된 Gaussian noise에서 시작하여 sample의 noise를 제거하기 위해 아래 과정을 $T$번 반복
    1. Denoiser를 이용해서 $\theta(\cdot)$을 예측
    2. 예측된 $\theta(\cdot)$을 활용해 $M_{t}$로부터 $M_{t-1}$을 얻음
       - $t > 1$일 때 $z \sim N(0, I)$, $t=1$일 때, $z = 0$

DiffSinger의 Inference 과정

• 최종적으로 $x$에 대한 mel-spectrogram $M$을 생성

$M_{t-1}$ 계산식

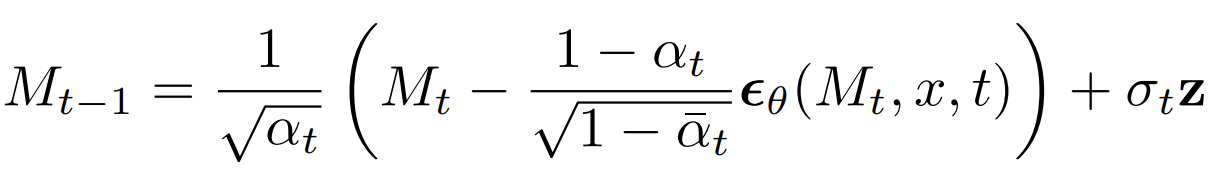
- Shallow Diffusion Mechanism

• DiffSinger에 많은 prior knowledge를 제공할 수 있는 ground-truth data 분포에 대한 strong connection을 보여주는 sample을 생성
• 해당 connection을 활용하기 위해 diffusion process에 대한 경험적인 관찰을 수행
  • $t=0$일 때, $M$은 합성된 보컬의 자연스러움에 영향을 주는 neighboring harmonics에 대한 풍부한 detail을 가지고 있지만, $\tilde{M}$은 over-smoothing을 보임
    - $\tilde{M}$ : L1 loss로 학습된 decoder의 mel-spectorgram
  • $t$가 증가함에 따라 두 process의 sample은 구별 불가능함

Diffusion process에 대한 step별 mel-spectrogram 변화

• Diffusion step이 충분히 클 때, $\tilde{M}$ manifold에서 Gaussian noise까지의 trajectory와 $M$에서 Gaussian noise manifold까지의 trajectory는 intersect 함

Diffusion trajectory

• Shallow Diffusion Mechanism
  • Gaussian noise에서 시작하지 않고, 두 trajectory의 intersection에서 reverse process를 시작하는 방식
    - Reverse process의 부담을 완화할 수 있음
    - $M_{k}$를 $M_{0}$로 변환하는 것은 Gaussian noise $M_{T}$를 $M_{0}$로 변환하는 것보다 쉽기 때문 ($k<T$)
  • Inference 단계에서,
    1. Auxiliary decoder를 활용하여 $\tilde{M}$을 생성
       - $\tilde{M}$은 악보 encoder output에 따라 조건을 가진 L1 loss로 학습됨
    2. Diffusion process를 통해 shallow step $k$에서 intermediate sample을 생성
       : $\tilde{M}_{k}(\tilde{M}, \epsilon) = \sqrt{\bar{\alpha}_{k}}\tilde{M} + \sqrt{1-\bar{\alpha}_{k}}\epsilon$
       - $\epsilon \sim N(0, I), \bar{\alpha}_{k} := \prod^{k}_{s=1} \alpha_{s}, \alpha_{k} := 1-\beta_{k}$
       - Intersection boundary $k$가 적절하게 선택되었다면, $\tilde{M}_{k}$와 $M_{k}$는 동일한 분포에서 왔다고 볼 수 있음
    3. $\tilde{M}_{k}$에서 reverse process를 수행하고 $k$번 반복해 denoising 함

- Boundary Prediction

• Intersection을 찾고 적응적으로 $k$를 결정하기 위해 Boundary Predictor (BP)를 활용
  • Mel-spectrogram에 noise를 추가하는 module과 classifier로 구성
  • Step number $t \in [0,T]$가 주어지면, $M_{t}$를 1, $\tilde{M}_{t}$를 0으로 하여 cross-entropy loss를 활용해 boundary predictor를 학습
    - Diffusion process의 $t$ step에서 입력된 mel-spectrogram이 $M$에서 오는지 $\tilde{M}$에서 오는지 판단
  • Training loss $L_{BP}$
    - $Y$ : mel-spectrogram의 training set

Boundary Predictor의 Training Loss

• BP의 학습이 완료되면, BP의 예측 값을 활용하여 $k$를 결정
  • 모든 $M \in Y$에 대해, $BP(M_{t}, t)$와 $BP(\tilde{M}_{t}, t)$사이의 margin이 threshold 이하인 95% step $t \in [k', T]$를 만족하는 가장 빠른 step $k'$을 찾음
  • $k'$의 평균을 intersection boundary $k$로 사용

- Model Structures

• Encoder
  • 악보를 condition sequence로 encoding 하는 역할
  • Encoder의 구성
    - Phoneme ID를 embedding sequence에 매핑하는 lyrics encoder와 linguistic hidden sequence로 변환하는 Transformer 블록
    - Linguistic hidden sequence를 mel-spectrogram의 length로 확장하는 Length regulator
    - Pitch ID를 pitch embedding sequence로 매핑하는 Pitch encoder
  • Encoder는 linguistic sequence와 pitch sequence를 music condition sequence $E_{m}$으로 활용
• Step Embedding
  • Diffusion step $t$는 denoiser $\theta$에 대한 조건부 입력
  • Discrete step $t$를 continous hidden으로 변환하기 위해, sinusodial positional embedding과 2개의 linear layer를 활용
    - $C$ channel을 가진 step embedding $E_{t}$를 얻음
• Auxiliary Decoder
  • FastSpeech2의 mel-spectrogram decoder와 동일하게 stacked Feed-Forward Transformer (FFT) 블록으로 구성
  • 최종 출력으로 $\tilde{M}$을 생성하는 단순한 mel-spectrogram decoder
• Denoiser
  • Denoiser $\theta$는 $\tilde{M}$을 입력으로 받아 step embedding $E_{t}$와 음악 condition sequence $E_{m}$에 조건을 둔 diffusion 과정에서 예측을 수행함
  • Non-casual WaveNet 구조를 denoiser로 사용
    - $H_{m}$ channel이 있는 $M_{t}$를 $C$ channel이 있는 hidden sequence $H$로 projection 하는 $1 \times 1$ convolution layer와 residual connection이 있는 $N$ convolution 블록으로 구성
  • 각 convolution 블록은:
    - $E_{t}$를 $H$에 더하는 element-wise adding operation
    - $H$를 $C$에서 $2C$ channel로 변환하는 non-casual convolution network
    - $E_{m}$을 $2C$ channel로 변환하는 $1 \times 1$ convolution layer
    - Input information과 condition을 merge 하는 gate unit
    - Merge 된 hidden을 $C$ channel이 있는 두 개의 분기로 분할하는 residual block
  • Denoiser가 최종 예측을 위해 여러 hierarchical level에서 feature를 통합할 수 있도록 함
• Boundary Predictor
  • Boundary Predictor의 classifier는 $E_{t}$를 얻기 위해 step embedding 수행
  • 이후 ResNet에 기반하여 $t$-th step에서 mel-spectrogram을 얻은 다음, $E_{t}$로 부터 $M_{t}$와 $\tilde{M}_{t}$를 분류

4. Experiments

- Settings

• Datasets : PopCS (Chinese Mandarin pop song dataset)
• Comparisons : FFT-NPSS, FFT-Singer, GAN-Singer

- Main Results and Analysis

• DiffSinger는 단순 Loss로 학습된 모델이나 GAN 기반 방법들에 비해 우수한 성능을 보임

DiffSinger와 비교모델 간의 MOS 비교

• 생성된 mel-spectrogram을 각각 비교해 보았을 때, DiffSinger는 harmonics 사이에 더 높은 detail을 포함함
• DiffSinger는 고주파 영역에서 높은 품질을 유지하면서 GAN-Singer보다 중저주파 영역에서 높은 성능을 보임

생성된 Mel-spectrogram 비교

• Shallow diffusion mechanism을 적용했을 때, naive diffusion 모델의 추론 속도가 45.1% 향상됨 (0.191 RTF vs. 0.348 RTF)
  - RTF : real-time factor, 1초에 오디오를 생성하는 데 걸리는 시간
• Shallow diffusion mechanism을 제거하면 -0.500 CMOS의 품질 저하가 발생
• Boundary predictor로 예측된 $k$가 아닌 다른 $k$값을 사용하면 품질 저하가 발생

DiffSinger에 대한 Ablation Study 결과

- Extensional Experiments on TTS

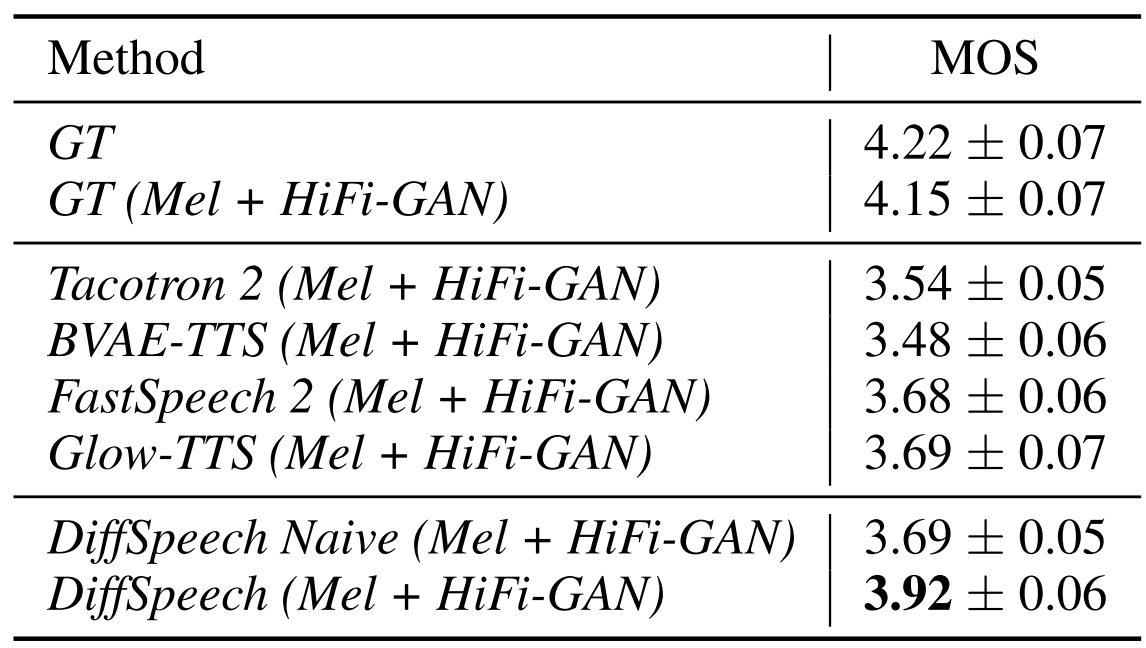
• Text-to-Speech (TTS)에 대한 일반화 여부를 확인하기 위해 LJSpeech dataset에 대해 실험을 수행
• DiffSinger가 FastSpeech2, Glow-TTS의 성능을 능가하며 TTS로의 일반화도 가능하다는 것을 제시
• TTS에서도 마찬가지로 shallow diffusion mechanism의 적용으로 인해 29.2%의 속도 향상을 달성함
  - 0.121 vs 0.171 RTF

DiffSinger를 TTS에 적용한 결과