[Paper 리뷰] ReFlow-TTS: A Rectified Flow Model for High-Fidelity Text-to-Speech

ReFlow-TTS: A Rectified Flow Model for High-Fidelity Text-to-Speech

---

• Diffusion model이 음성 합성에서 우수한 성능을 보이고 있지만, 고품질 음성 합성을 위해서는 여전히 많은 sampling step이 필요함 
• ReFlow-TTS
  • Rectified Flow를 활용한 Text-to-Speech 모델
  • Gaussian 분포를 straight line을 통해 ground-truth mel-spectrogram 분포로 transport 하는 Ordinary Differential Equation을 활용
• 논문 (ICASSP 2024) : Paper Link

---

1. Introduction

• Text-to-Speech (TTS)는 acoustic model과 vocoder를 활용하는 2-stage pipeline을 주로 활용함
  • Acoustic model은 text information을 mel-spectrogram으로 변환
  • Vocoder는 생성된 mel-spectrogram을 waveform으로 변환
  • 이때 합성된 음성 품질은 acoustic model에 의해 생성된 acoustic feature에 크게 의존함
• 최근 denoising diffusion probabilistic model (DDPM) 등을 활용한 diffusion model이 큰 주목을 받고 있음
  • Diffusion model은 고품질 합성이 가능하지만, 만족스러운 sample을 얻기 위해 많은 iteration이 필요하다는 단점이 있음
    - 결과적으로 느린 추론 속도로 이어짐
  • For example,
    - Diff-TTS는 DDPM framework를 기반으로 noise signal을 mel-spectrogram으로 변환
    - DiffSpeech는 shallow diffusion mechanism을 활용
    - Grad-TTS는 Stochastic Differential Equation (SDE)를 통해 noise를 mel-spectrogram으로 변환하고 numerical Ordinary Differential Equation (ODE) solver를 통해 reverse SDE를 solve
  • 위 방식들은 모두 고품질의 audio를 생성할 수 있지만, 여전히 reverse process에 대한 과정이 복잡함
    - 특히 CoMoSpeech의 경우 one-step generation을 위해 teacher model을 통한 distillation이 필요함

-> 그래서 Rectified Flow를 활용하여 sampling step을 줄이는 ReFlow-TTS를 제안

 

• ReFlow-TTS
  • Rectified Flow를 활용하여 추론 시 one-step sampling 만으로도 기존 보다 우수한 TTS 합성 품질을 달성
  • Pre-trained teacher model에 대한 의존성을 제거하여 합성 process를 간소화 가능

< Overall of ReFlow-TTS >

• Gaussian 분포를 straight line path를 통해 ground-truth mel-spectrogram 분포로 transport 하는 ODE 모델
• Unconstrained least squares optimization을 통해 학습되고, numerical ODE solver를 통해 high-fidelity의 음성을 합성 가능
• 추론 시 one sampling step만으로도 우수한 합성 성능을 달성하고, pre-trained teacher model에 대한 의존성을 제거함

2. Rectified Flow Model

• Rectified flow model은 분포 $\pi_{0}$에서 $\pi_{1}$까지 가능한 straight line path로 transport하는 ODE 모델
  - $\pi_{0}$ : standard Gaussian 분포, $\pi_{1}$ : ground-truth 분포

- Overview

• $X_{0} \sim \pi_{0}$과 $X_{1} \sim \pi_{1}$에 대한 empirical observation이 주어지면, $(X_{0}, X_{1})$에서 induce 된 rectified flow는, time $t \in [0,1]$에 대한 Ordinary Differential Equation (ODE)에 해당함
  • 이때 해당 ODE는:
    (Eq. 1) $dZ_{t}=v(Z_{t},t)dt$
    - 이를 통해 분포 $\pi_{0}$의 $Z_{0}$은 분포 $\pi_{1}$을 따르는 $Z_{1}$로 변환됨
    - $v$ : $X_{0}$와 $X_{1}$에 대한 linear path direction $(X_{1} -X_{0})$를 align 하는 방식으로 flow를 drive 하는 ODE의 drift force
  • 해당 mapping은 least square regression으로 solve 될 수 있음:
    (Eq. 2) $\min_{v} \int_{0}^{1}\mathbb{E}[||(X_{1}-X_{0})- v(X_{t},t)||^{2}]dt$
    - $X_{t} = tX_{1}+(1-t)X_{0}$
    - $X_{t}$ : $X_{0}$와 $X_{1}$에 대한 linear interpolation

• Naive 하게, $X_{t}$의 evolution은 ODE $dX_{t} = (X_{1}-X_{0})dt$를 따름
  • 이는 $X_{t}$를 update 하기 위해 final point $X_{1}$에 대한 dependency가 존재하기 때문에 non-casual 함
  • 이때 difference $(X_{1}-X_{0})$를 기반으로 하는 drift force $v$를 adjusting 하면,
    - Rectified flow는 linear interpolation $X_{t}$를 casualize 하므로, future state에 대한 knowledge 없이도 rectified flow를 simulation 할 수 있음
  • 이는 flow의 non-crossing property 측면에서 이해할 수 있음
    1. 해가 unique 하고 solvable 한 $dZ_{t} = v(Z_{t}, t)dt$와 같은 well-defined ODE를 따르는 경우,
       - 서로 다른 path는 time $t \in [0,1]$의 어느 point에서도 서로 cross 할 수 없음
    2. 다시 말해, 2개의 path가 서로 다른 direction을 따라 $z$에서 intersect 하는 location $z\in \mathbb{R}^{d}$와 time $t \in [0,1]$이 존재하지 않음
    3. 만약 그러한 crossing이 발생하는 경우 ODE의 해는 unique 하지 않게 나타남
  • Interpolation process $X_{t}$의 경우, path가 서로 intersect 할 수 있으므로 non-casual 함
    
    1. 이를 위해 rectified flow는 intersection point를 passing 하는 개별 trajectory를 adjust 하여 crossing을 방지함
       - 이와 동시에 linear interpolation path와 동일한 density map을 tracing 함
    2. 해당 alignment는 (Eq. 2)의 최적화를 통해 달성됨
  • Rectified flow는 non-crossing 방식으로 통과하는 particle traffic으로 볼 수 있음
    - 이를 통해 particle은 $X_{0}, X_{1}$ pair에 대한 global path information을 무시하는 대신, $(Z_{0}, Z_{1})$과 같은 deterministic pairing을 설정할 수 있음

- Training

• Rectified flow model을 training 하기 위해 (Eq. 2)를 solve 하여 parameter $\theta$를 학습
  • $\pi_{0}, \pi_{1}$에 대한 sample $(X_{0}, X_{1})$과 drift forced model $v_{\theta}$가 있을 때, training objective는:
    (Eq. 3) $\hat{\theta} = \arg \min_{\theta} \mathbb{E}[||(X_{1}-X_{0})-v(X_{t},t)||^{2}]$
    - $t \sim Uniform([0,1])$이고 $\hat{\theta}$는 learned optimal parameter
  • Training 이후, $dZ_{t} = v_{\hat{\theta}}(Z_{t},t)dt$에 따라 $v$를 얻고, sampling을 위해 $X_{0}\sim \pi_{0}$에서 시작하는 ODE를 solve 하여 $\pi_{0}$를 $\pi_{1}$로 transfer
  • 이때 procedure를 $Z = Reflow((X_{0},X_{1}))$으로 정의하면,
    1. 해당 procedure를 recursive 하게 적용하여 second rectified flow $Z^{2} = Reflow((Z_{0},Z_{1}))$을 얻을 수 있음
       - 여기서 $Z_{0}$는 Gaussian 분포의 sample이고 $Z_{1}$는 procedure $Z = Reflow((X_{0},X_{1}))$
    2. Recursive rectified flow는 transport cost를 줄이고 rectified flow path를 straightening 하여 linear flow trajectory를 얻을 수 있게 함
       - 이를 통해 straight path를 가지는 flow를 numerically simulating 할 때, time-discretization error를 최소화할 수 있음

Rectified Flow Model

3. ReFlow-TTS

- Rectified Flow Model for TTS

• ReFlow-TTS는 noise 분포를 time $t$와 text condition feature $c$에 대해 condition 된 mel-spectrogram 분포로 변환함
  • $\pi_{0}$를 standard Gaussian 분포로, $\pi_{1}$을 ground-truth mel-spectrogram data 분포라고 하면, $X_{0} \sim \pi_{0}, X_{1} \sim \pi_{1}$
  • 이때 ReFlow-TTS의 training objective는:
    (Eq. 4) $L_{\theta} = \mathbb{E}[ || (X_{1}-X_{0})-v_{\theta}(X_{t},t,c)||^{2}]$
    - 여기서 $t \in Uniform([0,1])$이고 $X_{t} = tX_{1} + (1-t)X_{0}$
    - ReFlow-TTS는 모델 $v_{\theta}$와 $(X_{1} -X_{0})$ output에 대한 L2 loss를 제외한 다른 auxiliary loss를 사용하지 않음
  • 추론 시에는 text feature $c$를 condition으로 하고, 모델 $v_{\theta}$를 기반으로 $Z_{0} \sim \pi_{0}$에서 시작하는 ODE를 directly solve 함
    - 이를 위해 RK45 ODE solver를 사용
    - One-step generation의 경우, Euler ODE solver를 사용
  • 추가적으로 recursive rectified flow를 활용하여 2-ReFlow-TTS를 구축할 수 있음
    - 2-ReFlow-TTS는 ReFlow-TTS에서 생성된 sample을 활용하여 re-train 됨

- Model Architecture

• ReFlow-TTS는 Text Encoder, Step Encoder, Duration Predictor, Length Regulator, Rectified Flow Decoder로 구성됨
  • Encoder, Duration Predictor, Length Regulator는 FastSpeech2를 기반으로 함
    - Enocder는 input text를 linguistic hidden feature로 encoding 하는 역할
    - Length Regulator는 Duration Predictor로 추출된 duration information을 기반으로 linguistic hidden feature를 해당 mel-spectrogram length로 확장하는 역할
  • Step Encoder는 256개 channel의 sinusoidal position embedding을 사용해 step $t$를 step embedding으로 변환
  • Rectified Flow Decoder는 DiffWave의 architecture를 활용
    - Deocder network는 Conv 1D, Tanh, Sigmoid, $1 \times 1$ convolution으로 구성된 residual block stack으로 구성됨

ReFlow-TTS Architecture

4. Experiments

- Settings

• Dataset : LJSpeech
• Comparisons : FastSpeech2, Grad-TTS, Diff-TTS, DiffSpeech, DiffGAN-TTS, ProDiff, CoMoSpeech

- Results

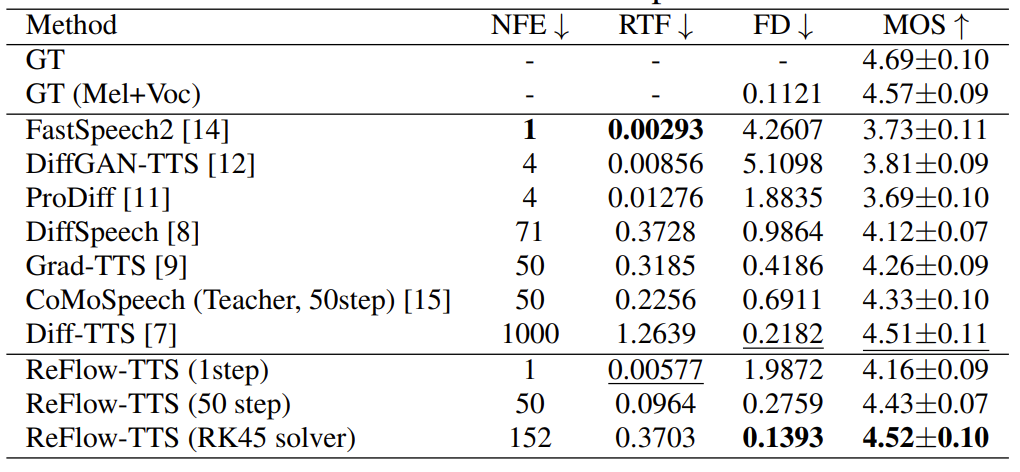
• Audio Performance
  • 합성 품질 측면에서 ReFlow-TTS가 가장 좋은 MOS와 FD score를 달성함
  • RTF 측면에서도 ReFlow-TTS는 다른 diffusion 기반의 TTS 모델들보다 빠른 속도를 보임

성능 비교 결과

• ReFlow-TTS로 생성된 mel-spectrogram은 다른 모델들보다 richer detail을 가짐
  - 결과적으로 더 natural 하고 expressive 한 음성을 합성 가능

Mel-Spectrogram 비교

• One sampling step만을 사용했을 때의 결과를 비교해 보면,
  • ReFlow-TTS는 기존의 one-step diffusion 방식인 CoMoSpeech와 비교할만한 결과를 얻음
  • 특히 ReFlow-TTS는 CoMoSpeech와 달리 pre-trained teacher model을 사용하지 않는다는 이점이 있음

One-Step Sampling에서의 합성 결과 비교

• 마찬가지로 one sampling step에서의 mel-spectrogram을 비교해 보면, ReFlow-TTS가 더 detail 한 spectrogram을 생성함

One-Step TTS에서의 Mel-Spectrogram 비교

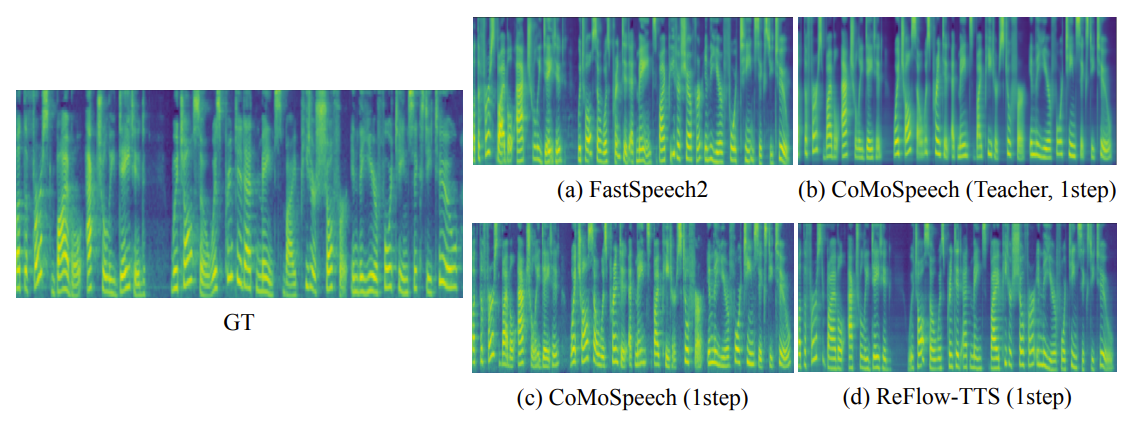
• 2-ReFlow-TTS는 Euler ODE solver와 RK45 ODE를 사용하여 더 빠른 추론 속도를 얻을 수 있음
  - Recursive rectified flow가 더 straight 하고 numerical computation이 쉽기 때문

2-ReFlow-TTS에 대한 성능 비교

• Mel-spectrogram 측면에서도 ReFlow-TTS와 2-ReFlow-TTS 모두 우수한 spectrogram을 생성하므로, 제안한 conditional rectified flow 방식이 효과적이라고 할 수 있음

2-ReFlow-TTS에 대한 Mel-Spectrogram 비교