[Paper 리뷰] RapFlow-TTS: Rapid and High-Fidelity Text-to-Speech with Improved Consistency Flow Matching

RapFlow-TTS: Rapid and High-Fidelity Text-to-Speech with Improved Consistency Flow Matching

---

• Ordinary Differential Equation 기반의 Text-to-Speech는 quality와 inference speed 간의 trade-off가 존재함
• RapFlow-TTS
  • Consistenct quality를 위해 Flow Matching-Straightened Ordinary Differential Equation trajectory를 따라 velocity field의 consistency를 enforce
  • Few-step synthesis의 quality를 향상하기 위해 time interval scheduling, adversarial learning을 적용
• 논문 (INTERSPEECH 2025) : Paper Link

---

1. Introduction

• Text-to-Speech (TTS)는 주어진 input text에 대해 high-fidelity speech를 생성하는 것을 목표로 함
  • 특히 Grad-TTS와 같은 Ordinary Differential Equation (ODE)-based model은 TTS에서 우수한 성능을 보임
    - BUT, diffusion model에서 얻어지는 ODE trajectory는 high-quality speech를 생성하기 위해 상당한 step이 필요하므로 slow inference speed를 가짐
  • 이를 해결하기 위해 CoMoSpeech와 같이 consistency distillation을 활용하거나 Matcha-TTS, VoiceFlow와 같이 Flow Matching (FM)을 활용할 수 있음
    - BUT, 여전히 inference speed와 speech quality 간에 trade-off가 존재함

-> 그래서 inference speed와 high-quality generation을 모두 만족하는 RapFlow-TTS를 제안

 

• RapFlow-TTS
  • Consistency FM을 기반으로 straight trajectory를 따라 consistent output을 생성
  • 추가적으로 shared dropout, Huber loss, time-interval scheduling, adversarial learning의 additional technique을 적용하여 sample quality를 개선

< Overall of RapFlow-TTS >

• High-fidelity few-step generation을 만족하는 Consistency FM 기반의 TTS model
• 결과적으로 2 step 만으로도 natural speech를 생성 가능

2. Consistency Flow Matching

• Consistency FM에서, time index $t\in [0,1]$은 uniform distribution으로부터 sampling 됨
  • 이때 FM은 random noise $x_{0}\sim p_{0}$에서 target data $x_{1}\sim p_{1}$ 까지의 probability path $p_{t}(x_{t})$를 build 하기 위해 ground-truth vector field $u_{t}$를 학습함
    1. 여기서 vector field는 flow $\phi_{t}$에 대한 ODE로 정의됨:
       (Eq. 1) $ \frac{d}{dt}\phi_{t}(x)=u_{t}\left(\phi_{t}(x)\right);\,\,\, \phi_{0}(x)=x$
       - $\phi_{t}$ : data를 time에 따라 transform 하는 function
       - (Eq. 1)의 solution인 flow는 sampling trajectory를 represent 함
    2. FM model training을 위해서는 다음과 같이 ground-truth vector field에 대한 simple regresion을 사용함:
       (Eq. 2) $\mathcal{L}_{FM}=\left|\left| v_{\theta}(t,x_{t})-u(t,x_{t})\right|\right|_{2}^{2}$
       - $v_{\theta}(t,x_{t})$ : learnable vector field network
  • Consistency FM은 trajectory의 모든 point가 same velocity로 same endpoint에 reach 하도록 training 됨
    1. 먼저 time $t$의 linearly interpolated noise sample을 $x_{t}=tx_{1}+(1-t)x_{0}$라고 하자
    2. 해당 objective function은 straight flow loss $\mathcal{L}_{sf}$와 velocity consistency loss $\mathcal{L}_{vc}$로 구성됨:
       (Eq. 3) $\mathcal{L}_{cfm}=\mathcal{L}_{sf}+\alpha\mathcal{L}_{vc}$
       $\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \mathcal{L}_{sf}=\left|\left| f_{\theta}(t,x_{t})-f_{\theta^{-}}(t+\Delta t, x_{t+\Delta t}) \right|\right|^{2}_{2}$
       $\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \mathcal{L}_{vc}=\left|\left| v_{\theta}(t,x_{t})-v_{\theta^{-}}(t+\Delta t, x_{t+\Delta t}) \right|\right|^{2}_{2}$
       $\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, f_{\theta}(t,x_{t})=x_{t}+(1-t)\times v_{\theta}(t,x_{t})$
       - $\theta^{-}$ : stop-gradient를 적용한 model parameter, $\alpha$ : loss weight, $\Delta t$ : time interval
    3. $f_{\theta}$는 $x_{t}$를 trajectory의 estimated endpoint로 guide 하므로, straight flow loss는 trajectory 측면에서 consistency를 constrain 함
       - Velocity consistency loss의 경우, vector field의 consistency를 directly enforce 함
    4. 이를 통해 FM은 straightened trajectory를 따라 consistent output을 생성하는 방법을 학습하고, few-step generation 만으로도 target distribution을 accurately estimate 할 수 있음

3. Method

- TTS with Consistency Flow Matching

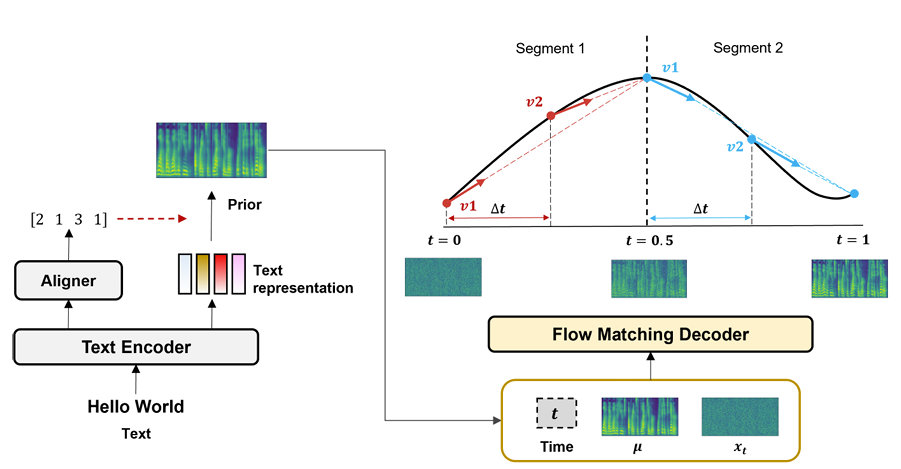
• RapFlow-TTS는 Matcha-TTS를 기반으로 text encoder, aligner, flow matching decoder로 구성됨
  • Text encoder는 input text에서 context representation을 추출하고, aligner는 해당 representation을 prior mel-spectrogram $\mu$에 mappping 함
    - Text encoder와 aligner는 Glow-TTS, Grad-TTS와 같이 Monotonic Alignment Search (MAS)로 얻어진 duration loss $\mathcal{L}_{dur}$, prior loss $\mathcal{L}_{prior}$를 사용하여 training 됨
  • Consistency FM은 FM decoder를 training 하여 random noise $x_{0}\sim p_{0}$를 target mel-spectrogram distribution $x_{1}\sim p_{1}$으로 transport 하는 probability path $p_{t}$를 construct 함
    1. 이때 주어진 input text에 해당하는 speech를 생성하기 위해 prior $\mu$로 consistency FM objective를 condition 함
       - 추가적으로 complex distribution 간의 flexible transportation을 위해 multi-segment objective를 채택함
    2. 즉, time range $t\in[0,1]$은 equal size의 $S$ segment로 divide 되고, 이때 각 segment는 time range $[i/S,(i+1)/S]$에 해당함 ($i=0,1,...,S-1$)
    3. 그러면 segmented consistency FM objective는:
       (Eq. 4) $\mathcal{L}_{cfm}=\mathcal{L}_{sf}+\alpha \mathcal{L}_{vc}$
       $\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \mathcal{L}_{sf}=\left|\left| f_{\theta}^{i}(t,x_{t},\mu) -f_{\theta^{-}}^{i}( t+\Delta t,x_{t+\Delta t},\mu)\right|\right|_{2}^{2}$
       $\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \mathcal{L}_{vc}=\left|\left| v_{\theta}^{i}(t,x_{t},\mu) -v_{\theta^{-}}^{i}( t+\Delta t,x_{t+\Delta t},\mu)\right|\right|_{2}^{2}$
       $\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, f_{\theta}^{i}(t,x_{t},\mu) =x_{t}+\left((i+1)/S-t\right)\times v_{\theta}^{i}(t,x_{t},\mu)$
    4. 결과적으로 RapFlow-TTS는 각 segment에서 consistent vector field로 straight flow를 학습하여 piecewise linear trajectory로 data distribution을 effectively represent 함
  • 한편으로 논문은 RapFlow-TTS를 optimize 하기 위해 two-stage training strategy를 활용함
  • First stage (first $N$ epoch)는 trajectory 측면에서 RapFlow-TTS가 straight flow를 가지도록 training 함
    1. 이를 위해 (Eq. 4)의 straight flow loss $\mathcal{L}_{sf}$ 만을 사용해 RapFlow-TTS를 training 함
    2. 이때 loss term은 $ \left|\left| f_{\theta}^{i}(t,x_{i}, \mu)-x^{i}\right|\right|_{2}^{2}$와 같이 modify 됨
       - $x^{i}$ : 각 segment의 ground-truth endpoint로써, $x^{i}=(i+1)/S\times x_{1}+(1-(i+1)/S)\times x_{0}$
       
    3. 해당 loss는 trajectory에서 ground-truth endpoint를 guide 하므로, RapFlow-TTS는 real data distribution을 represent 하는 straight flow의 vector field를 학습할 수 있음
  • Second stage ($N$ epoch 이후)에서는 (Eq. 4)의 entire $\mathcal{L}_{cfm}$을 사용하여 consistent vector field를 가진 straight flow를 가지도록 training 함
    - 이를 통해 RapFlow-TTS는 consistency와 straight flow의 property를 가지게 되므로, fewer step에서도 high-quality speech를 생성할 수 있음

Overview

- Improved Techniques for RapFlow-TTS

• 논문은 RapFlow-TTS의 consistency FM model의 few-step synthesis를 개선하기 위해 다음의 technique을 도입함
  • Encoder Freeze
    1. Second stage에서 encoder를 freeze 하고 training efficiency를 위해 $\mathcal{L}_{cfm}$만 optimize 함
    2. 추가적으로 $\mu$를 freeze 하여 consistency training을 stabilize 함
  • Shared Dropout
    1. Dropout을 적용하면 sample quality를 향상할 수 있으므로, second stage에서 $v_{\theta},v_{\theta^{-}}$에 대해 same random state를 사용하여 dropout을 적용함
    2. Dropout ratio은 $0.05$로 설정함
  • Pseudo-Huber Loss
    1. (Eq. 4)의 loss는 $\ell_{2}$ metric으로 구성됨
       - $\ell_{2}$ metric은 outlier에 large penalty를 impose 하여 time $t$에 대한 imbalanced loss를 발생시키므로, gradient variance가 증가할 수 있음
    2. 따라서 논문은 outlier에 less sensitive 한 pseudo-Huber metric $d(x,y)=\sqrt{||x-y||_{2}^{2}+c^{2}}-c$를 사용함
       - $d$ : data dimension size, $c=0.00054\sqrt{d}$
  • Delta Scheduling
    1. (Eq. 4)의 $\Delta t$는 trajectory의 두 point 간의 time interval을 represent 하는 parameter로써, diffusion-based consistency model의 discretization size parameter와 유사함
       - 즉, small $\Delta t$는 bias를 reduce 하지만 model variance를 increase 할 수 있고, large $\Delta t$는 variance를 reduce 하지만 bias를 increase 할 수 있다는 것을 의미함
    2. Training 마지막에는 small bias, large variance를 가지는 것이 desirable 하므로, 논문은 $\Delta t$를 progressively reduce 하는 delta scheduling을 도입함
    3. 이때 다양한 $\Delta t$에서 model을 uniformly training 하기 위해 linear step scheduling을 사용함
       - 결과적으로 $\Delta t$는 $K$ interval 동안 $0.1$에서 $0.001$로 decrease 하고, 각 $\Delta t$는 $N/K$ epoch 동안 사용됨
  • Adversarial Learning
    1. Synthesis quality를 향상하기 위해 second stage 이후에 adversarial learning을 적용함
       - 특히 mel-spectrogram level에서 Conv2D discriminator를 사용하여 MSE-based adversarial loss $\mathcal{L}_{adv}$와 feature matching loss $\mathcal{L}_{fm}$을 채택함
    2. 추가적으로 이를 consistency FM을 위한 multi-segment adversarial learning으로 extend 함
       - 먼저 $x^{i}, \hat{x}^{i}$를 각 segment의 ground-truth와 estimated endpoint라고 하면, $(i+1)/S\times x_{1}+(1-(i+1)/S)\times x_{0}$와 $f_{\theta}^{i}(t,x_{t},\mu)$를 얻을 수 있음
    3. 그러면 objective function은:
       (Eq. 5) $ \mathcal{L}_{adv}=\left|\left| D(\hat{x}^{i})\right|\right|_{2}^{2}+ \left|\left| 1-D(x^{i})\right|\right|_{2}^{2}$
       $\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \mathcal{L}_{fm}=\sum_{l=1}^{L}\left|\left| D^{l}(\hat{x}^{i})-D^{l}(x^{i})\right|\right|_{1}$
       - $D$ : discriminator, $D^{l}$ : $D$의 $l$-th feature map
       - 여기서 $\mathcal{L}_{cfm}, \mathcal{L}_{adv}, \mathcal{L}_{fm}$은 각각 $3,1,2$ ratio로 optimize 됨

4. Experiments

- Settings

• Dataset : LJSpeech, VCTK
• Comparisons : Grad-TTS, VoiceFlow, Matcha-TTS, FastSpeech2, CoMoSpeech

- Results

• LJSpeech dataset에 대해 RapFlow-TTS가 가장 우수한 성능을 달성함

LJSpeech에서의 성능

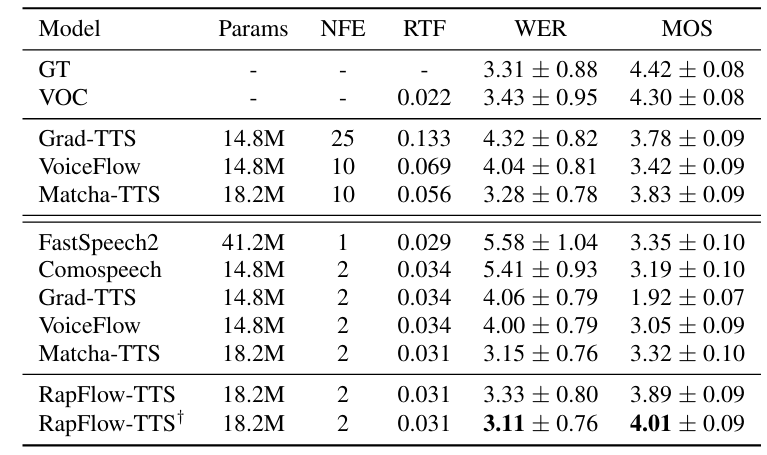
• VCTK dataset에 대해서도 뛰어난 성능을 보임

VCTK에서의 성능

• Ablation Study
  • 각 component는 RapFlow-TTS의 성능 향상에 유효함

Ablation Study