[Paper 리뷰] BigVSAN: Enhancing GAN-based Neural Vocoders with Slicing Adversarial Network

BigVSAN: Enhancing GAN-based Neural Vocoders with Slicing Adversarial Network

---

• Generative Adversarial Network (GAN) 기반의 vocoder는 빠르게 고품질의 waveform을 합성할 수 있다는 장점이 있음
  - BUT, 대부분의 GAN은 feature space에서 real/fake data를 discriminating 하기 위한 optimal projection을 얻지 못하는 것으로 나타남
• BigVSAN
  • Optimal projection을 얻을 수 있는 Slicing Adversarial Network (SAN)을 vocoding task에 적용한 모델 
  • GAN-based vocoder에서 채택되는 least-square GAN을 수정하여 loss function이 SAN의 요구사항을 만족하도록 함
• 논문 (ICASSP 2024) : Paper Link

---

1. Introduction

• Vocoder는 mel-spectrogram과 같은 intermediate representation을 waveform으로 합성하는 역할
  • Neural vocoder 구성을 위해 Autoregressive, Geneartive Adversarial Network (GAN), Flow-based, Diffusion model 등이 활용되고 있음
    - 특히 GAN은 고품질 합성과 빠른 생성 속도로 neural vocoder에서 가장 많이 활용되는 방식
  • 일반적으로 GAN의 discrimination process는 2단계로 구성됨
    1. Neural network를 통해 feature를 추출하고,
    2. Linear operation을 통해 feature를 1D space에 projection 하여 각 input이 real/fake인지를 판단
  • 이때 기존의 GAN-based vocoder들은 discriminator architecture에 주목하여 feature 추출 과정을 향상했음
    - BUT, Wasserstein GAN을 제외하고 대부분의 GAN은 feature space에서 real/fake에 대한 discriminative projection을 얻지 못하는 것으로 나타남
    - 따라서 이러한 discriminative projection 문제를 해결하기 위해 Slicing Adversarial Network (SAN)이 등장했고, 실제로 image 생성에서 우수한 성능을 보임

-> 그래서 neural vocoding task에 SAN framework를 적용한 BigVSAN을 제안

 

• BigVSAN
  • GAN-based vocoder에 SAN을 적용하는 최초의 시도
    - Minmax GAN, Hinge GAN과 같은 특수한 variant 대신 일반적으로 사용되는 least-sqaures GAN을 기반으로 함
  • 이때 least-squares GAN에 SAN framework를 적용하기 위해 soft monotonization 방식으로 objective를 수정하는 방식을 제안
    - 이를 통해 least-squares SAN을 얻고 training stability의 이점을 유지 가능

< Overall of BigVSAN >

• Least-squares GAN을 least-squares SAN으로 수정하는 soft monotonization scheme을 제시
• 결과적으로 기존 GAN-based vocoder의 성능을 간단한 수정만으로 크게 향상

2. Method

- Overall Framework

• Vocoder의 목표는 mel-spectrogram $s\in S$를 waveform signal $x\in X$로 변환하는 generator function $g_{\theta} : S\rightarrow X$를 train 하는 것
  • 이때 논문에서는 HiFi-GAN과 BigVGAN과 같은 GAN-based vocoder에 중점을 둠
  • 우선 HiFi-GAN과 BigVGAN에서는 ground-truth와 생성된 sample을 distinguish하기 위해 multi-scale discriminator $\{\phi_{k}\}_{k=1}^{K}$가 도입됨
    1. 이때 GAN training을 위한 maximization/minimization objective function을 각각 $\mathcal{V}_{GAN}(\phi_{k};\theta)$, $\mathcal{J}_{GAN}(\theta;\phi_{k})$로 나타낼 수 있음
    2. Discriminator로부터 얻은 intermediate feature는 pseudo-perceptual similarity metric인 feature matching loss $\mathcal{J}_{FM}(\theta;\phi_{k})$에도 사용됨
    3. 해당 loss 외에도 mel-spectrogram loss $\mathcal{J}_{mel}(\theta)$가 framework에 incorpoate 되어 주어진 mel-spectrogram과 생성된 waveform 간의 consistency를 보장함
  • 결과적으로 overall objective function은:
    (Eq. 1) $\max_{\{\phi_{k}\}_{k=1}^{K}}\sum_{k=1}^{K}\mathcal{V}_{GAN}(\phi_{k};\theta) $
    (Eq. 2) $\min_{\theta}\sum_{k=1}^{K}(\mathcal{J}_{GAN}(\theta;\phi_{k}) + \lambda_{FM}\mathcal{J}_{FM}(\theta;\phi_{k})+\lambda_{mel}\mathcal{J}_{mel}(\theta))$
    - $\lambda_{FM}, \lambda_{mel}$ : 각각 feature matching loss, mel-spectrogram loss에 대한 balancing parameter

- SANs for Vocoder Training

• 논문에서는 least-squares GAN을 기반으로 linear projection을 더 discriminative 하게 만드는 수정을 통해 least-squares SAN을 유도함
• From GANs to SANs
  • GAN을 SAN으로 수정하기 위해 GAN optimization의 sliced optimal transport perspective에서 시작하자
    1. 먼저 discriminator function $f: X\rightarrow \mathbb{R}$은 neural network $\phi$로 구성됨
       - 즉, linear operation과 non-linear activation의 combination을 가짐
    2. 이때 discriminator를 non-linear function $h_{\varphi}: X\rightarrow W\subseteq \mathbb{R}^{D}$와 last linear layer $w\in W$를 $f_{\varphi}^{w}(x)=w^{\top}h_{\varphi}(x)$로써 decompose
       - 즉, $\phi=\{ \varphi, w\}$
    3. 이때 discrimination process는 common projection $w$를 사용하여 non-linear feature $h_{\varphi}(x)$를 slicing 하는 것으로 interpret 할 수 있음
       
  • 결과적으로 위의 parameterization 하에서 discriminator와 generator에 대한 maximization, minimization objective는:
    (Eq. 3) $\mathcal{V}_{GAN}(\phi;\theta)=\mathbb{E}_{p_{X}}[R_{1}(f_{\varphi}^{w}(x))]+\mathbb{E}_{p_{S}}[R_{2}(f_{\varphi}^{w}(g_{\theta}(s)))]$
    (Eq. 4) $\mathcal{J}_{GAN}(\theta;\phi)=\mathbb{E}_{p_{S}}[R_{3}(f^{w}_{\varphi}(g_{\theta}(s)))]$
    - $p_{X}(x), p_{S}(s)$ : 각각 waveform signal과 mel-spectrogram의 data 분포
    - $R_{i} : \mathbb{R}\rightarrow \mathbb{R} (i=1,2,3)$의 choice와 관련하여 여러 GAN variant를 사용 가능함
  • Maximization 문제의 최적화를 통해 non-linear function $h_{\varphi}$를 유도하여 feature space $W$에 mapping 되는 real/fake sample을 separate 하여 $W$에서 linear projection으로 잘 discriminate 되도록 할 수 있음
    1. BUT, (Eq. 3)을 maximize 하는 linear projcetion $w$는 discrimination을 위한 feature를 제대로 활용할 수 없음
    2. 한편 $h_{\varphi}$가 주어졌을 때 (Eq. 3)을 maximize하는 projection $w$보다 discrimination 측면에서 더 유용한 informative linear projection이 존재하는 것이 발견됨
       - 이를 위해 $W$에서 real/fake sample을 가장 잘 distinguish 할 수 있는 last projection layer를 학습하는 것을 목표로 하는 SAN이 제안됨
    3. 실제로 $R_{3}$의 derivative인 $r_{3}$가 monotonically decreasing function이면, 모든 GAN은 SAN으로 변환될 수 있음
       - 즉, derivative $r_{3}(z)$는 모든 $z\in\mathbb{R}$에 대해 음수여야 함
  • 결과적으로 위의 condition 하에서, last linear layer의 normalization과 GAN의 maximization problem modification을 통해 SAN에 대한 objective를 얻을 수 있음:
    (Eq. 5) $\mathcal{V}_{SAN}(\varphi,\omega,\theta)=\mathbb{E}_{p_{X}}[R_{1}(f_{\varphi}^{\omega -}(x))]+\mathbb{E}_{p_{S}}[R_{2}(f_{\varphi}^{\omega -}(g_{\theta}(s)))]+\mathbb{E}_{p_{X}}[R_{3}(f_{\varphi -}^{\omega}(x))]-\mathbb{E}_{p_{S}}[R_{3}(f_{\varphi -}^{\omega}(g_{\theta}(s)))]$
    (Eq. 6) $\mathcal{J}_{SAN}(\theta ; \varphi,\omega)=\mathbb{E}_{p_{S}}[R_{3}(f_{\varphi}^{\omega}(g_{\theta}(s)))]$
    - 여기서 last linear layer는 unit hypersphere $\mathbb{S}^{D-1}$로 normalize 됨 (즉, $\omega=w/||w||_{2}$)
    - $(\cdot) -$ : stop-graident operator가 있는 parameter
  • 위 objective에서 desired direction은 $R_{1}, R_{2}$가 아니라 $R_{3}$에 대한 maximization problem에 따라 달라짐
    - 직관적으로 optimal $\omega$는 $\tilde{p}_{X}(x)\propto r_{3}\circ f(x)p_{X}(x)$, $\tilde{p}_{\theta}(x)\propto r_{3}\circ f(x)p_{\theta}(x)$일 때, 각각 $\mathbb{E}_{\tilde{p}_{X}}[h(x)], \mathbb{E}_{\tilde{p}_{\theta}}[h(x)]$를 가장 잘 separate 함
    - $p_{\theta}(x)$ : $p_{S}(s)$와 generator function $x=g_{\theta}(s)$로 주어지는 generator 분포
• Soft Monotonization for Least-Squares SAN
  • Vocoder training을 위한 대부분의 GAN-based 모델은 다음의 least-squares GAN objective를 활용함:
    (Eq. 7) $R_{1}(z)=-(1-z)^{2}, \, R_{2}(z)=-z^{2},\, R_{3}(z)=(1-z)^{2}$
    - 이때 function $R_{3}$는 square operator로 인해 monotonically decreasing function이 아님
    - 따라서 앞선 SAN 변환 procedure를 least-squares GAN에 적용하면 유효한 SAN 모델을 얻을 수 없음
  • 이때 SAN을 구성하기 위해 least-squares GAN 대신 hinge GAN이나 non-saturating GAN을 활용하면 되지만, vocoding task에서는 해당 variant들을 SAN으로 대체했을 때 만족스럽지 못한 결과가 얻어짐
    - 실제로 기존의 vocoder들도 training stability로 인해 모두 least-squares GAN을 기반으로 하고 있으므로, 논문에서도 마찬가지로 least-squares SAN을 구성하는 것을 목표로 함
  • 결과적으로 least-squares SAN 구성을 위해 (Eq. 7)을 다음과 같이 수정함:
    (Eq. 8) $\tilde{R}_{1}(z)=-\varsigma(1-z)^{2},\, \tilde{R}_{2}=-\varsigma(z)^{2},\, \tilde{R}_{3}=\varsigma(1-z)^{2}$
    - $\varsigma(\cdot)$ : softplus function으로써 soft monotonization이라고 함 (즉, $\varsigma(a) = \log(1+e^{a})$)
  • 위를 통해 $\tilde{R}_{3}$은 monotonic condition을 만족하게 되므로, (Eq. 8)을 (Eq. 5), (Eq. 6)에 대입하여 least-squares SAN에 대한 minmax objective를 구성할 수 있음
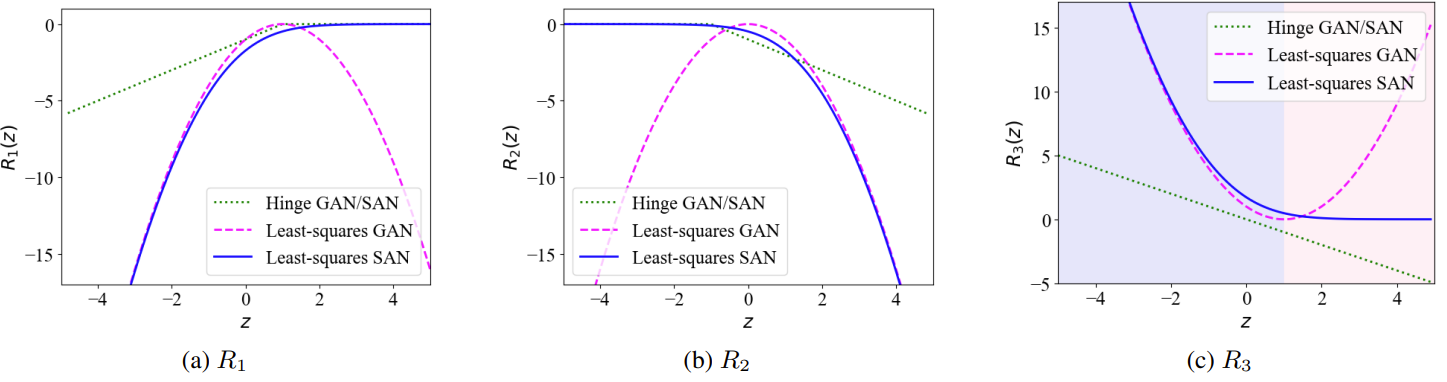
    1. 즉, 아래 그림과 같이 $R_{3}$의 shape를 유지하면서 monotonically decreasing 하는 $\tilde{R}_{3}$를 설계 가능
       - 아래 그림의 (c)에서 least-squares GAN의 $R_{3}$는 빨간색으로 표시된 부분에서 증가하는데, 이는 non-monotonicity의 문제를 발생시켜 SAN의 unstability을 야기함
       - 반면 수정된 objective를 사용하는 least-sqaures SAN은 $R_{3}$에서 전체 실수에 대해 monotonically decreasing 하고, 파란색으로 표시된 부분에서 기존 least-squares GAN의 shape를 그대로 유지함
    2. 이를 통해 least-sqaures SAN에서도 least-squares GAN의 training stability를 유지할 수 있고, 실험적으로도 (Eq. 8) 대신 (Eq. 7)을 채택했을 때 unstable training이 발생하는 것으로 나타남
       

Monotonicity 비교

- BigVSAN: Large-Scale Vocoder Training

• Large-scale GAN-based vocoder인 BigVGAN에 위에서 유도된 (Eq. 5), (Eq. 6)의 SAN training framework를 적용하여 BigVSAN을 얻음
  • 이때 BigVGAN은 least-squares GAN에 의존하기 때문에 유효한 SAN 모델을 얻기 위해서는 (Eq. 8)의 soft monotonization을 적용해야 함
  • 여기서 log-scale parameterization $f_{\{\alpha,\beta\}}(x)=x+e^{-\beta}\sin^{2}(e^{\alpha}x)$를 사용하는 snakebeta activation을 모델에 추가적으로 적용할 수 있음
    - $\alpha, \beta$ : trainable parameter
    

3. Experiments

- Settings

• Dataset : LibriTTS, LJSpeech, VCTK
• Comparisons : BigVGAN, MelGAN, Parallel WaveGAN

- Results

• LibriTTS에서 합성 품질을 평가했을 때, BigVSAN은 모든 정량적/주관적 평가에서 BigVGAN 보다 뛰어난 성능을 보임

성능 비교 결과

• 한편 Snakebeta activation을 적용하는 경우, MCD와 M-STFT는 저하되지만 MOS 측면에서는 더 좋은 결과를 보임
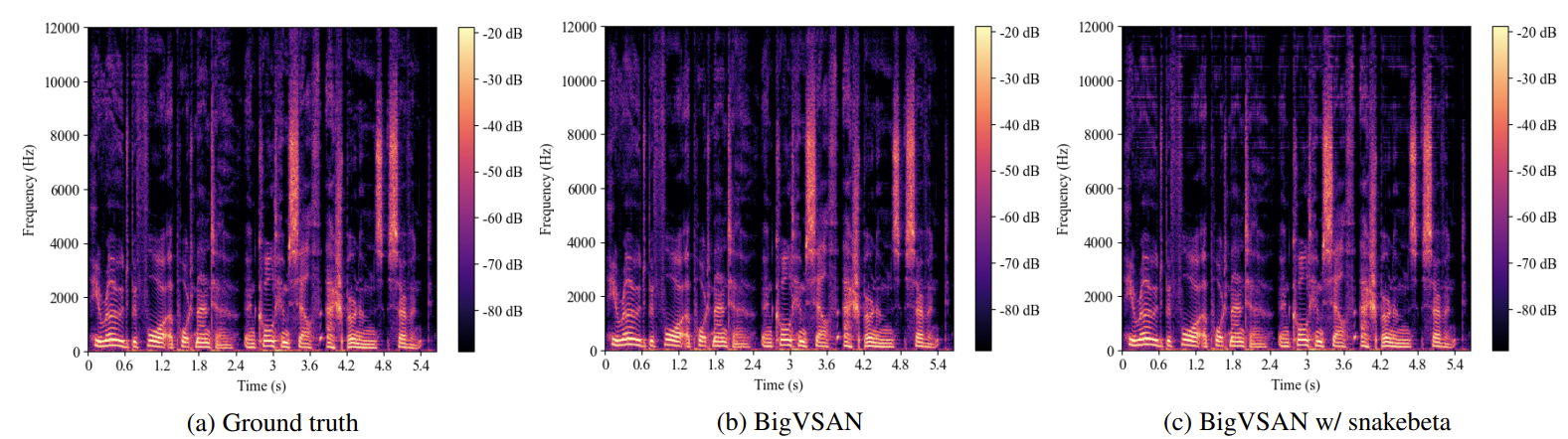
  • 이는 아래 mel-spectrogram과 같이 snakebeta activation이 high-frequency band에서 artifact를 생성하기 때문
  • 결과적으로 $[0,8]$ kHz 이상의 high frequency band를 고려하여 계산되는 MCD, M-STFT에서는 성능이 저하되어 나타남
  • 반면 human rater에게는 high-frequency component가 perception에 크게 영향을 미치지 않기 때문에 MOS는 상반되게 나타남

Mel-Spectrogram 비교

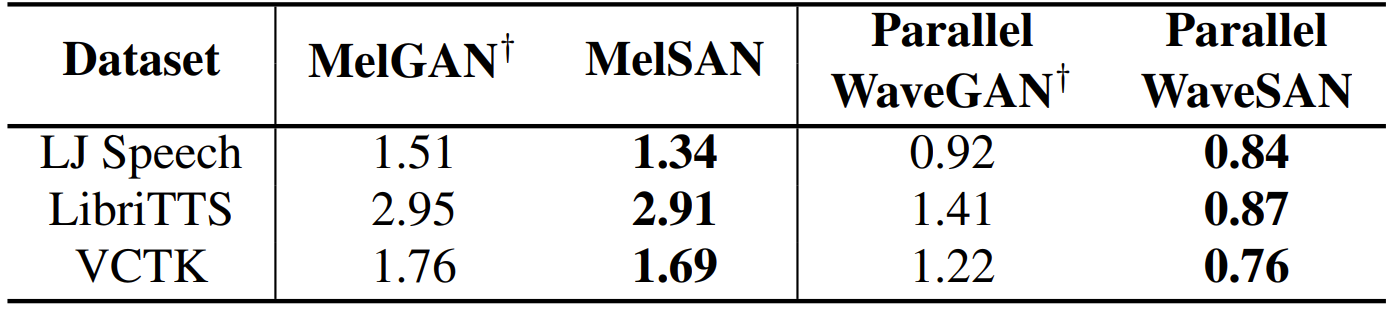
• BigVGAN과 같은 large-scale 모델이 아닌 일반적인 크기의 neural vocoder에 SAN을 적용해 보면
  • 결과적으로 MelGAN, Parallel WaveGAN을 SAN으로 대체한 MelSAN, Parallel WaveSAN이 더 우수한 성능을 보임
  • 즉, GAN에 대한 간단한 modification 만으로도 neural vocoder의 성능을 크게 향상할 수 있음

SAN과 GAN의 성능 비교