[Paper 리뷰] CM-TTS: Enhancing Real Time Text-to-Speech Synthesis Efficiency through Weighted Samplers and Consistency Models

CM-TTS: Enhancing Real Time Text-to-Speech Synthesis Efficiency through Weighted Samplers and Consistency Models

---

• Text-to-Speech에서 diffusion model을 사용하면 high-fidelity의 음성을 합성할 수 있지만 multi-step sampling으로 인해 real-time synthesis에는 한계가 있음
• 한편으로 GAN과 diffusion model을 결합하여 denoising distribution을 근사하는 방식으로 추론 속도를 개선할 수 있지만, adversarial training으로 인해 모델 수렴의 어려움이 있음
• CM-TTS
  • Consistency Model (CM)을 기반으로 adversarial training이나 pre-train model dependency 없이 더 적은 step으로 continuous-time diffusion model에서 고품질 음성 합성을 지원
  • 추가적으로 dynamic probability를 통해 다양한 sampling position을 모델에 반영하여 training process에서 unbiased learning을 보장하는 weighted sampler를 도입
• 논문 (NAACL 2024) : Paper Link

---

1. Introduction

• Text-to-Speech (TTS) 모델은 크게 autoregressive (AR), non-autoregressive (NAR) 방식을 활용할 수 있음
  • AR framework는 attention mechanism을 기반으로 한 RNN model을 사용해 spectrogram을 sequential 하게 생성함
    - 안정적인 합성을 보장할 수 있지만, prediction error가 accumulate 되고 추론 속도가 느리다는 한계가 있음
  • NAR framework의 경우, AR framework와 달리 parallel feed-forward network를 통해 complexity를 줄이고 real-time 합성을 지원할 수 있음
    - 실제로 GAN, Flow-based model은 TTS에서 성공적으로 사용되고 있음
    - 특히 최근의 diffusion model은 noise addition이 포함된 forward diffusion process와 parameterized reverse iterative denoising process를 사용하여 고품질 합성 능력을 보임
  • BUT, diffusion model은 고품질 TTS가 가능하다는 장점에도 불구하고 Markov chain으로 인한 multi-step iterative sampling으로 인해 효율성의 근본적인 한계가 있음
    1. 이때 CoMoSpeech는 consistency model을 도입하여 해당 문제를 해결함
       - Well-designed diffusion-based teacher model에서 consistency constraint를 적용해 distil 한 model을 활용하여 singe diffusion step으로 음성을 합성하는 방식
       - BUT, 해당 방식은 teacher model에 대한 distillation에 의존하므로 training pipeline이 복잡하고, multi-speaker 환경으로 constraint를 확장하기 어려움
    2. 한편으로 DiffGAN-TTS의 경우, GAN을 diffusion model에 통합함으로써 sampling step을 줄임
       - BUT, 해당 방식은 discriminator에 대한 additional training으로 인해 모델 수렴의 어려움이 있음
    3. 그 외에도 추론 속도 향상을 위해 DiffSinger와 같이 shallow diffusion mechanism을 고려할 수 있음
       - BUT, pre-trained model을 추가하는 경우 architecture가 복잡해짐

-> 그래서 teacher model의 distillation에 의존하지 않고 diffusion TTS의 추론 속도를 개선하는 consistency model인 CM-TTS를 제안

 

• CM-TTS
  • Continuous-time diffusion과 consistency model을 기반으로, 음성 합성을 generative consistency procedure로 frame 하여 single-step 만으로도 우수한 합성 품질을 달성
    - 특히 이를 통해 기존 diffusion TTS 모델에서 사용된 adversarial training, auxiliary pre-trained model에 대한 의존성을 제거함
  • 추가적으로 weighted sampler를 도입하여 training efficiency를 향상하고 sampling bias를 mitigate 함

< Overall of CM-TTS >

• Consistency model을 기반으로 효율적인 real-time, few-step iterative generation이 가능
• Single-step generation을 지원하고, additional adversarial training, pre-trained model에 대한 의존성을 제거
• 다양한 sampling point에 대한 weight를 adjust 하는 weighted sampler를 도입하여 training process를 향상
• 결과적으로 zero-shot, few-shot TTS에서 우수한 품질을 달성하면서 빠른 합성이 가능 

2. Background: Consistency Models

• Diffusion model은 target dataset에 Gaussian noise를 sequentially add 한 다음 reverse denoising process를 수행하는 방식으로 동작함
  • 해당 iterative method는 initially noise state에서 sample을 생성하여 data의 intrinsic structure를 효과적으로 capture 하도록 설계됨
  • 먼저 time constant $T$에 대해 noisy data sequence $\{x\}_{t\in [0,T]$가 있다고 하자
    1. 그러면 diffusion process는 다음의 stochastic differential equation (SDE)를 통해 나타낼 수 있음:
       (Eq. 1) $\mathbf{x}_{t}=\mu(\mathbf{x}_{t}, t)dt+\sigma(t)d\mathbf{W}_{t}$
    2. 여기서 $p_{0}(\mathbf{x}) \equiv p_{data}(\mathbf{x})$이고, $p_{T}(\mathbf{x})$는 Gaussisan distribution으로 근사됨
       - $t\in[0,T]$ : forward diffusion time step의 index
       - $\mu(.,.), \sigma(.)$ : 각각 drift, diffusion coefficient
       - $\{w_{t}\}_{t\in[0,T]}$ : standard Brownian motion
  • 이때 SDE는 probability flow ODE 형태로 나타나는 well-defined reverse process를 가지고 있으므로, time $t$에서 sampling 된 trajectory는 $p_{t}(\mathbf {x}_{t})$에 대한 distribution을 따름:
    (Eq. 2) $d\mathbf{x}_{t}=\left[\mu(\mathbf{x}_{t},t)-\frac{1}{2}\sigma(t)^{2}\nabla\log p_{t}(\mathbf{x}_{t})\right]dt$
    - $\nabla p_{t}(\mathbf{x}_{t})$ : score function
  • Diffusion model에서 forward step은 noise level에 따라 data distribution에서 멀어지도록 shift를 유도하고, backward step은 sample을 expected data distribution에 가까워지도록 guide 함
    
    1. 특히 sample generation을 위한 (Eq. 2)의 probability flow ODE는 score function $\nabla \log p_{t}(\mathbf{x}_{t})$를 활용함
    2. 이때 score function을 얻기 위해서는 denoising error $|| f(x_{t},t)-x||^{2}$를 최소화해야 함:
       (Eq. 3) $\nabla\log p_{t}(\mathbf{x}_{t})=\frac{(f(x_{t},t)-x_{t})}{\sigma(t)^{2}}$
       - $f(x_{t},t)$ : step $t$에서 sample $x_{t}$를 refine 하는 denoiser function
    3. 한편으로 probability flow ODE에 대한 sampling은 2-step approach를 따름
       - 먼저 noise distribution에서 sample을 추출하고,
       - 다음으로 Euler / Heun과 같은 numerical ODE solver를 사용하여 denoising process를 수행함
  • BUT, 위와 같은 ODE solver를 통한 sampling process는 상당한 iteration이 필요하므로, 추론 속도가 느림
    1. 따라서 diffusion model의 sampling을 가속화하기 위해, 모든 time step $t$와 solution trajectory의 $t'$에 대해 다음의 consistency property를 도입함:
       (Eq. 4) $f(x_{t},0)=f(x_{t'},t'),\,\,\, f(x_{t},0)=x_{0}$
       - 위의 condition이 주어지면, ODE의 sampling trajectory를 따르는 각 point들이 origin $p_{0}(x)$와 직접 연관되므로 one-step sampling $f(x_{T},T)$가 가능해짐
    2. 한편으로 consistency model은 consistency training이나 pre-trained diffusion-based teacher model로부터의 distillation을 사용하여 구축될 수 있음
       - Distillation 방식은 teacher model에 종속되므로 TTS pipeline이 복잡해짐
       - 따라서 CM-TTS는 consistency training을 기반으로 consistency model을 설계함

3. CM-TTS

• Diffusion model은 TTS에서 우수한 합성 품질을 얻을 수 있지만, 느린 sampling으로 인해 real-time으로 동작하기 어려움
  - CM-TTS는 consistency model 도입을 통해 해당 문제를 극복하고자 함

- Model Overview

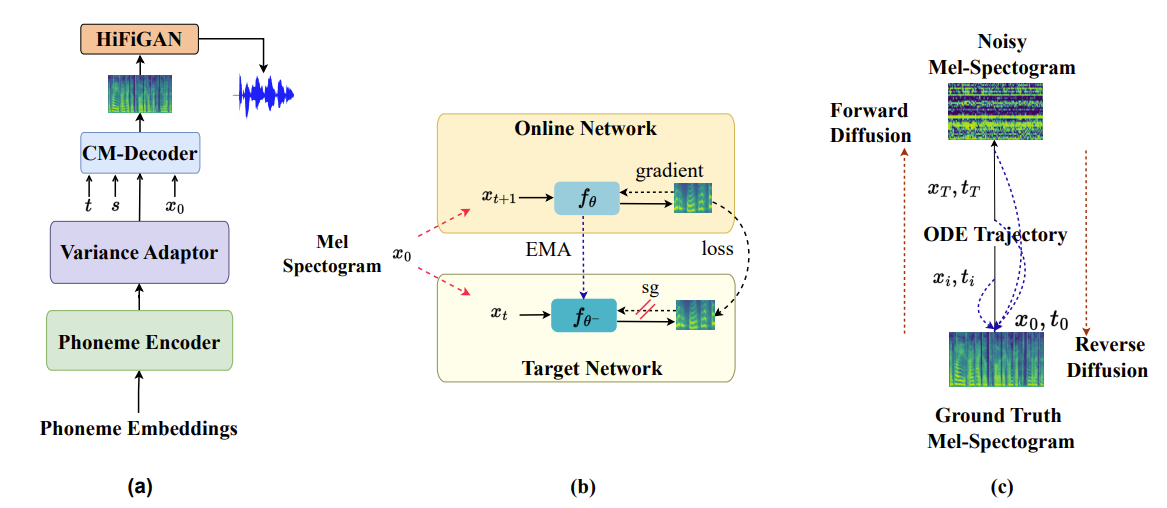
• CM-TTS는 크게 4가지 component로 구성됨
  1. Phoneme encoder : text processing을 수행하는 역할
  2. Variance adaptor : pitch, duration, energy feature를 예측하는 역할
  3. CM-decoder : mel-spectrogram generation을 수행하는 역할
  4. Vocoder : HiFi-GAN을 기반으로 mel-spectrogram을 time-domain waveform으로 변환하는 역할

(a) CM-TTS architecture (b) Decoder Training Scheme (c) ODE trajectory

- Phoneme Encoder and Variance Adaptor

• Phoneme encoder는 transformer block을 활용한 feed-forward network를 adapt 하여 phoneme sequence 내의 local dependency를 capture 함
  • Variance adaptor는 FastSpeech2를 따라 convolution block으로 구성된 pitch, energy, duration predictor로 구성됨
    - 이때 training을 위해 ground-truth에 대한 Mean Squared Error (MSE) loss $\mathcal{L}_{duration}, \mathcal{L}_{pitch}, \mathcal{L}_{energy}$를 사용
  • Training phase에서 ground-truth duration은 phoneme encoder의 hidden sequence를 확장하여 frame-level hidden sequence를 생성한 다음, ground-truth pitch information을 통합하여 사용됨
    - 추론 시에는 예측된 duration과 pitch value를 활용

- Consistency Models

• Time hoizon $[\epsilon, T_{\max}]$ 내의 division을 위해, interval은 $t_{1}=\epsilon<t_{2}<...<t_{N}=T_{\max}$ boundary의 $N-1$ sub-interval로 segment 됨
  • 이때 EDM을 따라 numerical instability를 완화하기 위해 $\epsilon=0.002$의 small positive value로 설정하고, $T_{\max}=80$으로 설정함
  • 그러면 mel-spectrogram을 $\mathbf{x}$라 하고, $\mathbf{x}_{0}$를 noise가 추가되지 않은 initial mel-spectrogram이라고 하자
    1. Consistency model $f_{\theta}$를 formulate 하기 위해서는 (Eq. 4)에서 정의된 self-consistency property를 적용하여 data에서 consistency function을 학습해야 함
    2. 이때 $f_{\theta}(x_{0},\epsilon)=\mathbf{x}_{0}$을 보장하기 위해, consistency model $f_{\theta}$는 다음과 같이 parameterize 됨:
       (Eq. 5) $f_{\theta}(\mathbf{x},t)=c_{skip}(t)\mathbf{x}+c_{out}(t)F_{\theta}(\mathbf{x},t)$
       - $c_{skip}, c_{out}$ : differentiable function으로써, $c_{skip}(\epsilon)=1, c_{out}(\epsilon)=0$
       - $F_{\theta}(\mathbf{x},t)$ : neural network
  • Self-consistency property를 enforce 하기 위해 target model $\theta^{-}$는 online network $\theta$와 concurrent 하게 유지됨
    1. 이때 target network $\theta^{-}$의 weight는 학습을 위해 intend 된 parameter $\theta$에 대한 Exponential Moving Average (EMA)로 update 됨:
       (Eq. 6) $\theta^{-}\leftarrow \mathrm{stopgrad}(\mu\theta^{-}+(1-\mu)\theta)$
    2. 결과적으로 consistency loss $\mathcal{L}_{CT}^{N}(\theta,\theta^{-})$는:
       (Eq. 7) $\sum_{n\geq 1}\mathbb{E}[\lambda(t_{n})d(f_{\theta}(\mathbf{x}_{t+1}), f_{\theta^{-}}(\mathbf{x}_{t}))]$
       - $d(\cdot, \cdot)$ : squared $l_{2}$ distance $d(x,y)=||x-y||_{2}^{2}$와 같이 두 sample 간의 distance를 나타내는 function
       
  • $\mathbf{x}_{t+1}$과 $\mathbf{x}_{t}$는 training data $\mathbf{x}_{0}\sim D(\text{dataset})$의 mel-spectrogram에서 시작하여 forward diffusion process를 적용한 다음, probability flow ODE의 trajectory를 따라 두 point를 sampling 하여 얻어짐:
    (Eq. 8) $\mathbf{x}_{t+1}=\mathbf{x}_{0}+t_{n+1}\mathbf{z},\,\,\, \mathbf{x}_{t}=\mathbf{x}_{0}+t_{n}\mathbf{z}$
    - $\mathbf{z}\sim\mathcal{N}(0,I)$
    - 여기서 step $t_{n}$은:
    (Eq. 9) $t_{n}=\left[{T_{\max}}^{\frac{1}{p}}+\frac{n-1}{N-1}\left(\epsilon^{\frac{1}{p}}-{T_{\max}}^{\frac{1}{p}}\right) \right]^{p}$
    - $N$ : sub-interval, $n$ : weighted sampling strategy와 $p=7$을 사용하여 interval $[1,N-1]$에서 sampling 되는 값
  • DiffGAN-TTS와 마찬가지로 CM-TTS의 $F_{\theta}(\mathbf{x},t)$ architecture는 non-causal WaveNet structure를 활용함
    1. 대신 sampling과정에서 $t$에 대한 approach를 다르게 사용하고, CM-TTS는 동일한 architecture를 가진 2개의 decoder $f_{\theta}, f_{\theta^{-}}$가 각각 online, target network 역할을 하도록 함
    2. 추가적으로 CM-TTS의 diffusion process는 (Eq. 8)로 characterize 되지만, DiffGAN-TTS는 parameter-free $T$-step Markov chain을 사용함

- Training and Loss

• 논문에서는 online $f_{\theta}$와 target $f_{\theta^{-}}$의 2개의 decoder를 사용하여 training 함
  • 먼저 $\mathbf{x}_{t+1},\mathbf{x}_{t}$의 state를 활용하여 online, target network를 통해 각각 $f_{\theta}(\mathbf{x}_{0}+t_{n+1}\mathbf{z}), f_{\theta^{-}}(\mathbf{x}_{0}+t_{n}\mathbf{z})$로 express 되는 mel prediction을 얻음
    - Online component는 해당 prediction pair 간의 MSE loss를 통해 gradient update를 수행하고, 동시에 target network의 gradient는 EMA를 통해 update 됨
    
  • Training 중에 online/target network는 iterative interplay에 engage 하여 mutual learning과 model stability에 기여함
    1. 이때 mel reconsturction loss $\mathcal{L}_{mel}$은 ground-truth와 생성된 mel-spectrogram 간의 Mean Absolute Error (MAE)로 계산됨
    2. 그러면 $\mathcal{L}_{recon}$은:
       (Eq. 10) $\mathcal{L}_{recon}=\mathcal{L}_{mel}(\mathbf{x}_{0},\hat{\mathbf{x}}_{0})+\lambda_{d}\mathcal{L}_{duration}(\mathbf{d},\hat{\mathbf{d}})+\lambda_{p}\mathcal{L}_{pitch}(\mathbf{p},\hat{\mathbf{p}})+\lambda_{e}\mathcal{L}_{energy}(\mathbf{e},\hat{\mathbf{e}})$
       - $\mathbf{h},\mathbf{p},\mathbf{e}$ : ground-truth duration, pitch, energy
       - $\hat{\mathbf{h}}, \hat{\mathbf{p}}, \hat{\mathbf{e}}$ : predicted value
       - $\lambda_{d}, \lambda_{p}, \lambda_{e}$ : 각 loss component에 대한 weight로, 논문에서는 0.1로 설정
    3. 결과적으로 CM-TTS training을 위한 optimization objective는:
       (Eq. 11) $\mathcal{L}_{CM\text{-}TTS}=\mathcal{L}_{CT}^{N}(\theta,\theta^{-})+\mathcal{L}_{recon}$
       
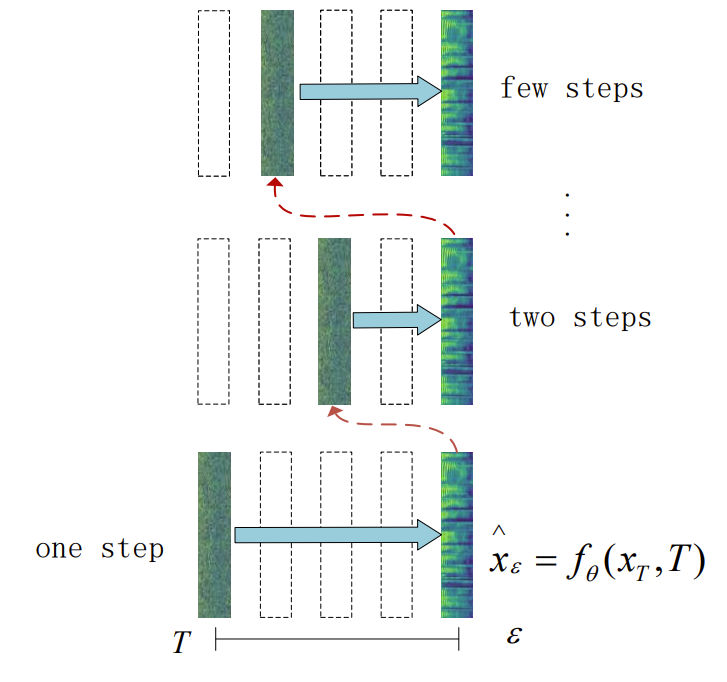
  • 추론 과정에서 $f_{\theta}$를 통한 single forward pass를 수행하여 single-step generation이 가능함
    - 한편으로 아래 그림과 같이 denoising과 noise injection step을 altering 하여 품질을 더욱 향상할 수 있는 multi-step generation을 수행할 수도 있음 

Single-step, Multi-step Inference

- Weighted Sampler

• Training procedure는 (Eq. 9)에서 정의된 time step $t_{n}$에 대한 sampling에 의존함 
  • 결과적으로 논문은 ODE trajectory를 따라 다양한 position ($t_{n}$)을 sampling 하는 것의 영향력을 알아보기 위해, 3가지의 sampling strategy를 비교함
    - 여기서 각 strategy는 training 전반에 걸쳐 $t_{n}$ step selecting과 관련된 probability를 관리함
  • 먼저 training 시 forward diffusion process에서 variable $n$은 sampling point의 index로써 $n\in[1,N-1]$이고, $t_{n}$을 계산하기 위해 (Eq. 9)에서 사용됨
    - 그러면 sampler에 의해 current index $n$에 할당된 weight를 $c_{n}$이라 하고, index $n$을 selecting 할 probability $s_{n}=\frac{c_{n}}{\sum_{i=1}^{N-1}c_{n}}$으로 나타낼 수 있음
  • 결과적에서 논문에서 비교하는 3가지 sampler design은:
    1. Uniform Sampler
       - 각 point가 equal probability $c_{n}=1$로 choice 되는 baseline sampler
    2. Linear Sampler
       - Sampling weight가 sampling point에 따라 linear 하게 변화하는 sampler
       - $c_{n}=\alpha\cdot n$으로 정의되고, 논문에서는 $\alpha=1$로 설정
    3. Importance Sampler (IS)
       - Sampling point에 weight를 할당하는 방식으로써, $c_{n}=(1-\phi)\frac{\sum_{j=1}^{H}L(t,j)}{\sum_{i=1}^{N-1}\sum_{j=1}^{H}L(i,j)}+\phi$로 정의됨
       - $L\in\mathbb{R}^{(N-1)\times H}$는 모든 sampling point에 대한 historical loss를 recording 하는 matrix이고, $H$는 각 point에 store 된 historical loss 수 (논문에서는 10으로 설정)
       - $\phi$ : $c_{n}$을 adjusting 하는 balancing factor
       - 해당 IS는 historical loss를 기반으로 current sampling probability를 adjust 하여 model training에 중요한 point들을 prioritizing 함 

4. Experiments

- Settings

• Dataset : VCTK, LJSpeech
• Comparisons : FastSpeech2, VITS, DiffSpeech, DiffGAN-TTS

- Results

• Comparison with Baselines
  • CM-TTS는 기존 모델들과 비교하여 가장 우수한 성능을 보임
  • 특히 CM-TTS는 single-step generation ($T=1$)에서도 뛰어난 성능을 달성함

• Few-step Speech Generation
  • Single step에 대해 CM-TTS는 DiffGAN-TTS 보다 지속적으로 우수한 성능을 보임
  • 한편으로 $T=4$의 multi-step synthesis로 확장하여도 높은 성능을 보임

모델 성능 비교

• Ablation Study
  • Ablation study 측면에서 CT와 IS를 각각 제거해 보면, WER 측면에서 성능 저하가 크게 발생함
  • 즉, 각 component는 모델 성능 향상에 유효함

Ablation Study 결과

• Length Robustness During Training
  • Training에서 variable-length sequence를 가지는 경우, loss 계산에 padding을 통합하여 사용할 수 있음
    - 이를 통해 input data와 padded segment 모두에서 meaningful representation을 capture 하도록 함
  • 결과적으로 아래 표와 같이 loss 계산에서 padding을 포함하면 모델의 성능이 개선됨
    

Loss Padding의 효과

• The Impact of Weighted Sampler
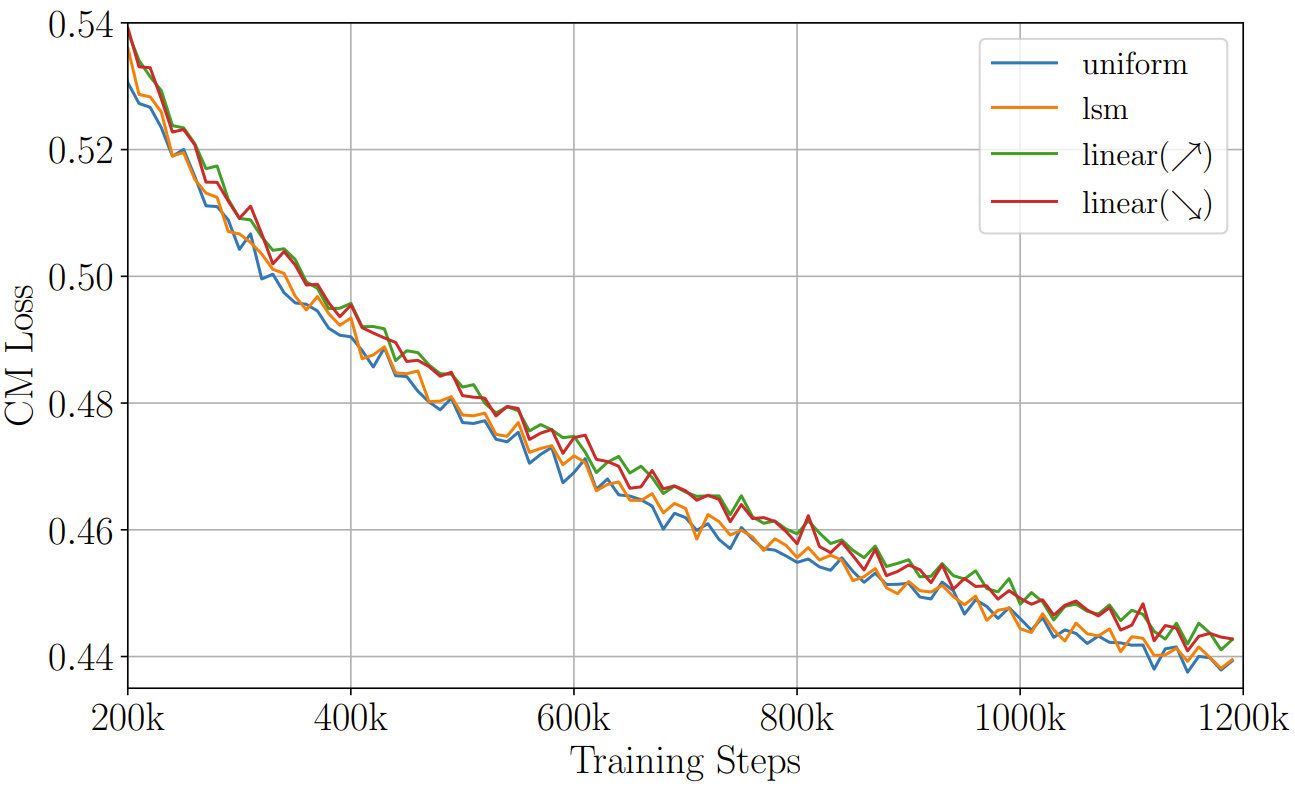
  • CM-TTS에 다양한 sampling method가 미치는 영향을 알아보면, IS sampler를 사용할 때 가장 높은 성능을 얻을 수 있음
  • 한편으로 다른 sampler를 사용하더라도 CM-TTS의 수렴에는 큰 영향을 주지 않음

다양한 Sampler 비교

Sampler 사용에 따른 모델 수렴 비교

• IS sampler의 generalization 측면에서, DiffGAN-TTS에 IS를 적용해 보면 마찬가지로 성능 개선의 효과를 얻을 수 있음

DiffGAN-TTS에 IS Sampler를 적용했을 때의 결과

• Generalization to Unseen Speakers
  • Unseen speaker에 대한 zero-shot 성능을 확인해 보면, CM-TTS의 성능이 가장 우수한 것으로 나타남
  • 추가적으로 multi-speaker scenario에서도 CM-TTS는 DiffGAN-TTS 보다 뛰어남

Zero-Shot TTS 성능

Multi-Speaker Scenario에서 Prosody 비교