[Paper 리뷰] DiffVC: Diffusion-based Voice Conversion with Fast Maximum Likelihood Sampling Scheme

DiffVC: Diffusion-based Voice Conversion with Fast Maximum Likelihood Sampling Scheme

---

• One-shot many-to-many voice conversion은 source/target speaker가 모두 training dataset에 속하지 않은 경우에 대해서 single reference utterance의 target voice를 copy 하는 것을 목표로 함
• DiffVC
  • Diffusion probabilistic modeling을 기반으로 scalable one-shot voice conversion을 수행
  • 추가적으로 diffusion model을 가속할 수 있는 Stochastic Differential Equation solver를 설계
• 논문 (ICLR 2022) : Paper Link

---

1. Introduction

• Voice Conversion (VC)는 source speaker utterance의 linguistic content를 유지하면서 target speaker voice를 copy 함
  • 특히 one-shot VC는 target speaker voice를 copy 하기 위해 single reference utterance만을 사용하는 것을 목표로 함
    
  • 기존의 one-shot VC model은 latent space에 encoded utterance의 linguistic content만을 포함하면서, target voice information은 speaker embedding으로써 decoder에 conditioning 되는 AutoEncoder를 도입함
    - 대표적으로 AutoVC는 pre-trained speaker verification network로 얻어진 speaker embedding을 활용
  • BUT, AutoEncoder VC model은 decoder conditioning 외에도 encoder에서 source speaker identity와 speech content를 disentangle 할 수 있어야 함
    - 이를 위해 VQVC+, VQMIVC는 content information에 Vector Quantization을 적용
    - AdaIN-VC, AGAIN-VC는 Instance Normalization layer를 활용
  • 한편으로 VC 성능을 더욱 향상하기 위해 Diffusion Probabilistic Model (DPM)을 활용할 수 있음

-> 그래서 diffusion model을 기반으로 하는 one-shot VC model인 DiffVC를 제안

 

• DiffVC
  • Disentanglement 문제를 해결하기 위해 average voice를 예측하는 encoder를 활용
    - 즉, 각 phoneme에 해당하는 mel-feature를 large-scale multi-speaker dataset에서 average 된 mel-feature로 변환하도록 training 함
  • WaveGrad, DiffWave와 같이 speech-related task에서 우수한 성능을 보이는 DPM 기반 decoder를 채택
    - BUT, DPM 기반 decoder는 forward pass scheme이 iterative 하므로 추론 속도가 상당히 느림
  • 따라서 고품질 sample 생성에 대한 iteration 수를 줄이고 추론 속도를 향상하기 위해 Likelihood Maximization에 기반한 DPM solver를 설계

< Overall of DiffVC >

• Diffusion model을 기반으로 하는 one-shot VC model
• Likelihood Maximization에 기반한 DPM sampling scheme을 통해 추론 속도를 개선
• 결과적으로 기존보다 뛰어난 conversion 성능을 달성하면서 빠른 sampling이 가능

2. Voice Conversion Diffusion Model

• DiffVC는 기존의 VC model들과 마찬가지로 AutoEncoder를 기반으로 함
  • 특히 data-dependent prior (forward diffusion의 terminal distribution)를 가지는 모든 conditional DPM은 다음과 같이 취급할 수 있음:
    - Encoder : data에 Gaussian noise를 추가하는 forward diffusion
    - Decoder : 해당 noise를 remove 하는 reverse diffusion
  • 이때 DPM은 forward/reverse diffusion process trajectory 간의 distance를 minimize 하도록 training 됨
    - 이는 AutoEncoder 측면에서 reconstruction error를 minimize 하는 것과 같음
  • Data-dependent piror는 Grad-TTS, PriorGrad를 따르는 continuous DPM framework를 활용

Overall of DiffVC

- Encoder

• DiffVC는 speaker-independent speech representation으로써 average phoneme-level mel-feature를 채택함
  • 이때 encoder를 통해 input mel-spectrogram을 average voice의 mel-spectrogram으로 변환할 수 있도록, 다음의 과정을 통해 training 함:
    
    1. Montreal Forced Aligner를 large-scale multi-speaker dataset에 적용하여 phoneme과 speech frame을 align 함
    2. 다음으로 전체 dataset에서 mel-feature를 aggregate 하여 각 특정 phoneme에 대한 average mel-feature를 얻음
    3. 최종적으로 encoder는 output mel-spectrogram과 ground-truth average voice mel-spectrogram 간의 Mean Squared Error를 minimize 하도록 training 됨
       
  • 구조적으로 encoder는 Grad-TTS의 transformer-based architecture를 따름
    - 대신 input으로 character/phoneme embedding이 아닌 mel-feature를 사용하고, decoder와 개별적으로 training 됨

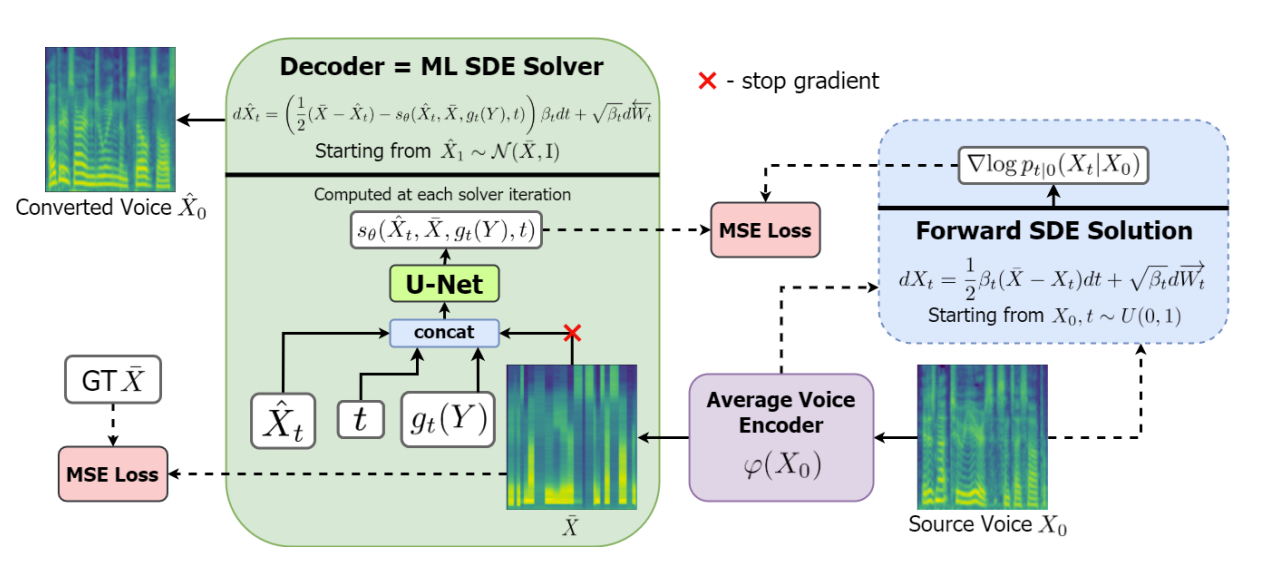
- Decoder

• Encoder는 forward diffusion (prior)의 terminal distribution을 parameterize 되는 반면, reverse diffusion은 decoder를 통해 parameterize 됨 
  • 이때 논문은 Score-based Modeling에 따라 Ito calculus를 사용하여 discrete-time Markov chain이 아닌 stochastic process로 diffusion을 정의함
    1. 먼저 일반적인 DPM framework는 다음의 Stochastic Differential Equation (SDE)과 같은 forward/reverse diffusion으로 구성됨:
       (Eq. 1) $dX_{t}=\frac{1}{2}\beta_{t}(\bar{X}-X_{t})dt+\sqrt{\beta_{t}}d\overrightarrow{W_{t}}$
       (Eq. 2) $d\hat{X}_{t}=\left(\frac{1}{2}(\bar{X}-\hat{X}_{t})-s_{\theta}( \hat{X}_{t},\bar{X},t)\right)\beta_{t}dt+\sqrt{\beta_{t}}d\overleftarrow{W_{t}}$
       - $t\in[0,1]$이고, $\overrightarrow{W_{t}},\overleftarrow{W_{t}}$는 $\mathbb{R}^{n}$에서의 independent Wiener process
       - $\beta_{t}$ : nosie schedule과 같은 non-negative function, $s_{\theta}$ : parameter $\theta$를 가지는 score function
       - $\bar{X}$ : $n$-dimensional vector
    2. Grad-TTS에 따라 (Eq. 1)의 forward SDE는 explicit solution을 가짐:
       (Eq. 3) $\text{Law}(X_{t}|X_{0})=\mathcal{N}\left(e^{-\frac{1}{2}\int_{0}^{t}\beta_{s}ds}X_{0} +\left(1-e^{-\frac{1}{2}\int_{0}^{t}\beta_{s}ds}\right)\bar{X},\left(1-e^{-\int_{0}^{t}\beta_{s}ds}\right)I\right)$
       - $I$ : $n\times n$ identity matrix
       - 이때 nosie가 $\beta_{0}, \beta_{1}$에 대해 linear schedule $\beta_{t}=\beta_{0}+t(\beta_{1}-\beta_{0})$을 따르고 $e^{-\int_{0}^{1}\beta_{s}ds}$가 0에 가깝다면, $\text{Law}(X_{1})$은 DPM의 prior인 $\mathcal{N}(\bar{X},I)$에 가까워짐
    3. (Eq. 2)의 reverse diffusion은 weighted $L2$ loss를 minimize 하여 training 됨:
       (Eq. 4) $\theta^{*}=\arg\min_{\theta}\mathcal{L}(\theta)=\arg\min_{\theta}\int_{0}^{1}\lambda_{t} \mathbb{E}_{X_{0},X_{t}}|| s_{\theta}(X_{t},\bar{X},t)-\nabla\log p_{t|0}(X_{t}|X_{0})||_{2}^{2}dt$
       - $p_{t|0}(X_{t}|X_{0})$ : (Eq. 3)의 conditional distribution에 대한 Probability Density Function (PDF)
       - $\lambda_{t}=1-e^{-\int_{0}^{t}\beta_{s}ds}$
       
    4. (Eq. 3)의 distribution은 Gaussian이므로:
       (Eq. 5) $\nabla\log p_{t|0}(X_{t}|X_{0})=-\frac{X_{t}-X_{0}e^{-\frac{1}{2}\int_{0}^{t}\beta_{s}ds }- \bar{X}(1-e^{-\frac{1}{2}\int_{0}^{t}\beta_{s}ds})}{1-e^{-\int_{0}^{t}\beta_{s}ds}}$
  • Training 시 time variable $t$는 $[0,1]$에서 uniformly sample 되고, noise sample $X_{t}$는 (Eq. 3)에 따라 생성되고, loss function $\mathcal{L}$은 해당 sample로부터 (Eq. 5)를 통해 계산됨
    1. $X_{t}$는 intermediate value $\{X_{s}\}_{0<s<t}$를 계산할 필요 없이 sampling 될 수 있으므로 (Eq. 4)의 optimization task에 대한 time, memory efficiency를 향상할 수 있음
    2. (Eq. 2)의 reverse diffusion은 (Eq. 1)의 forward diffusion과 가까운 trajectory를 가지므로, DPM으로 data를 생성하기 위해서는 prior $\mathcal{N}(\bar{X},I)$에서 $\hat{X}_{1}$을 sampling 한 다음 (Eq. 2)의 SDE를 backward solve 하면 됨 
• 앞선 DPM을 voice conversion task를 위해 사용하기 위해, DiffVC는 다음의 수정 사항을 반영함:
  • 먼저 $\bar{X}=\varphi(X_{0})$로 취급
    - $\varphi$ : encoder, $\bar{X}$ : target voice로 conversion 하고자 하는 average voice mel-spectrogram
  • Decoder $s_{\theta}(\hat{X}_{t}, \bar{X},g_{t}(Y),t)$를 trainable function $g_{t}(Y)$로 condition 하여 target speaker information을 제공
    - $Y$ : 추론 시에는 target mel-spectrogram의 forward trajectory, training 시에는 training mel-spectrogram의 forward trajectory
  • 이때 해당 trainable function은 decoder와 jointly train 되는 neural network로 구성되고, 다음의 3가지 input type을 가질 수 있음:
    1. $d\text{-}only$ : pre-trained speaker verification network를 사용하여 target mel-spectrogram $Y_{0}$에서 추출된 speaker embedding
    2. $wodyn$ : noisy target mel-spectrogram $Y_{t}$를 input으로 추가
    3. $whole$ : forward diffusion $\{Y_{s}|s=0.5/15,1.5/15, ...,14.5/15\}$ 하에서 target mel-spectrogram의 whole dynamics를 추가
  • 구조적으로 decoder architecture는 U-Net을 기반으로 함
    - Speaker conditioning network $g_{t}(Y)$는 2D convolution과 MLP로 구성되고, additional 128 channel로써 $\hat{X}, \bar{X}$의 concatenation에 broadcast-concatenate 되어 128-dimensional vector를 output 함

3. Maximum Likelihood SDE Solver

• 논문은 forward diffsuion의 sample path에 대한 log-likelihood를 maximize 하는 fixed-step first-order reverse SDE solver를 설계함
  • 먼저 $t\in[0,1]$에 대해 Euclidean space $\mathbb{R}^{n}$으로 정의된 forwar/reverse SDE가 있다고 하자:
    (Eq. 6-F) $dX_{t}=-\frac{1}{2}\beta_{t}X_{t}dt+\sqrt{\beta_{t}}d\overrightarrow{W_{t}}$
    (Eq. 6-R) $d\hat{X}_{t}=\left(-\frac{1}{2}\beta_{t}\hat{X}_{t}-\beta_{t}s_{\theta}(\hat{X}_{t},t)\right)dt+\sqrt{\beta_{t}}d\overleftarrow{W_{r}}$
    - $\overrightarrow{W}$ : forward Wiener process (여기서 forward increments $\overrightarrow{W_{t}}-\overrightarrow{W_{s}}$는 $t>s$에 대해 $\overrightarrow{W_{s}}$와 independet 함)
    - $\overleftarrow{W}$ : reverse Wiener process (여기서 reverse increments $\overleftarrow{W_{s}}-\overleftarrow{W}$는 $s<t$에 대해 $\overleftarrow{W_{t}}$와 independent 함)
  • 그러면 Score-based Modeling에 따라 (Eq. 6)의 DPM을 Variance Preserving (VP)으로 볼 수 있고, simplicity를 위해 논문은 해당 diffusion model에 대한 Maximum Likelihood solver를 유도함
    1. VC diffusion model에 대한 앞선 (Eq. 1)은 constant shift를 통해 (Eq. 6-F)의 Mean Reverting-Variance Preserving (MR-VP)로 변환될 수 있음
    2. 이때 (Eq. 6-F)의 forward SDE는 explicit solution을 가짐:
       (Eq. 7) $\text{Law}(X_{t}|X_{s})=\mathcal{N}(\gamma_{s,t}X_{s},(1-\gamma_{s,t}^{2})I),\,\,\, \gamma_{s,t}=\exp\left(-\frac{1}{2}\int_{s}^{t}\beta_{u}du\right)$
       - $\forall \,\, 0\leq s<t\leq 1$
    3. Neural network $s_{\theta}$로 parameterize 된 (Eq. 6-R)의 reverse SDE는 noise data $X_{t}$의 log-density에 대한 gradient를 근사하도록 training 됨:
       (Eq. 8) $\theta^{*}=\arg\min_{\theta}\int_{0}^{1}\lambda_{t}\mathbb{E}_{X_{t}}|| s_{\theta}(X_{t},t)-\nabla\log p_{t}(X_{t})||_{2}^{2}dt$
       - Expectation은 PDF $p_{t}(\cdot)$을 가지는 noisy data distribution $\text{Law}(X_{t})$에 취해지고, $\lambda_{t}$는 positive weighting function을 의미
  • 이때 DiffVC는 다음 두 condition을 모두 만족한다고 가정함:
    1. Certain Lipschitz constraint는 strong solution의 존재를 보장하기 위해 (Eq. 6)의 SDE coefficient에 의해 satisfy 되어야 함
    2. Optimal $\theta^{*}$에 대해 (Eq. 6-R)의 reverse SDE로 생성된 path $\hat{X}$는 (Eq. 6-F)의 forward SDE로 생성된 path $X$와 distribution 내에서 동일하다는 것이 보장되어야 함
  • VP DPM의 generative procedure는 $\hat{X}_{1}\sim\mathcal{N}(0,I)$에서 시작하여 (Eq. 6-R)의 reverse SDE를 time-backward로 solve 하는 것으로 구성됨
    1. BUT, Euler-Maruyama solver는 discretization error로 인해 iteration 수가 적을 때 sample 품질을 저하시킴
       - 한편으로 특정한 SDE type에 대해 unbiased numerical solver나 exact solver를 설계할 수 있음
    2. 결과적으로 [Theorem 1.]은 diffusion model에 대해 (Eq. 6-F)의 forward diffusion을 사용하고 likelihood 측면에서 general-purpose Euler-Maruyama solver 보다 더 나은 reverse SDE solver를 가질 수 있음을 의미함
    3. 이때 [Theorem 1.]의 solver는 다음과 같이 정의된 value들을 사용:
       (Eq. 9) $\mu_{s,t}=\gamma_{s,t}\frac{1-\gamma_{0,s}^{2}}{1-\gamma_{0,t}^{2}},\,\,\, \nu_{s,t}=\gamma_{0,s}\frac{1-\gamma_{s,t}^{2}}{1-\gamma_{0,t}^{2}},\,\,\, \sigma_{s,t}^{2}=\frac{(1-\gamma_{0,s}^{2})(1-\gamma_{s,t}^{2})}{1-\gamma_{0,t}^{2}}$
       (Eq. 10) $\kappa_{t,h}^{*}=\frac{\nu_{t-h,t}(1-\gamma_{0,t}^{2})}{\gamma_{0,t}\beta_{t}h}-1,\,\,\, \omega_{t,h}^{*}=\frac{\mu_{t-h,t}-1}{\beta_{t}h}+\frac{1+\kappa_{t,h}^{*}}{1-\gamma_{0,t}^{2}}-\frac{1}{2},$
       $\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, (\sigma_{t,h}^{*})^{2}=\sigma_{t-h,t}^{2}+\frac{1}{n}\nu_{t-h,t}^{2}\mathbb{E}_{X_{t}}\left[ \text{Tr}(\text{Var}(X_{0}|X_{t}))\right]$
       - $n$ : data dimensionality, $\text{Var}(X_{0}|X_{t})$ : conditional data distribution $\text{Law}(X_{0}|X_{t})$에 대한 covariance matrix
       - 따라서 $\text{Tr}(\text{Var}(X_{0}|X_{t}))$는 모든 $n$-dimension에 대한 overall variance이고, expectation $\mathbb{E}_{X_{t}}[\cdot]$은 unconditional noisy data distribution $\text{Law}(X_{t})$에 대해 적용됨
  • [Therorem 1.]
    Reverse diffusion으로 optimality까지 train 된 (Eq. 6)의 SDE로 characterize 된 DPM이 있다고 하자. 임의의 자연수 $N\in\mathbb{N}$에 대해 $h=1/N$일 때, 실수 triplet $\left\{ (\hat{\kappa}_{t,h},\hat{\omega}_{t,h},\hat{\sigma}_{t,h})|t=h,2h,...,1\right\}$으로 parameterize 된 fixed step size $h$에 대한 reverse SDE solver는:
    (Eq. 11) $\hat{X}_{t-h}=\hat{X}_{t}+\beta_{t}h\left(\left(\frac{1}{2}+ \hat{\omega}_{t,h}\right)+(1+\hat{\kappa}_{t,h})s_{\theta^{*}}(\hat{X}_{t},t)\right)+\hat{\sigma}_{t,h}\xi_{t} $
    여기서 $\theta^{*}$는 (Eq. 8)로 얻어지고, $t=1,1-h,...,h$, $\xi_{t}$는 $\mathcal{N}(0,I)$의 $i.i.d.$ sample이다. 그러면:
    1. Generative model $\hat{X}$ 하에서 sample path $X=\{X_{kh}\}_{k=0}^{N}$의 log-likelihood는 $\hat{\kappa}_{t,h}=\kappa_{t,h}^{*},\hat{\omega}_{t,h}=\omega_{t,h}^{*}, \hat{\sigma}_{t,h}=\sigma_{t,h}^{*}$에 의해 maximize 된다.
    2. (Eq. 11)의 SDE solver가 random variable $\hat{X}_{1}\sim\text{Law}(X_{1})$에서 시작한다고 가정하자. 이때 $X_{0}$가 constant이거나 diagonal isotropic covariance matrix를 가지는 Gaussian random variable (i.e., $\delta>0$일 때 $\delta^{2}I$)인 경우, generative model $\hat{X}$는 $\hat{\kappa}_{t,h}=\kappa_{t,h}^{*},\hat{\omega}_{t,h}=\omega_{t,h}^{*},\hat{\sigma}_{t,h}=\sigma_{t,h}^{*}$에 대해 exact 하다.
  • 결과적으로 [Theorem 1.]은 standard method에 비해 additional computation이 필요 없는 개선된 DPM sampling method를 제공하고, re-training이나 noise schedule space search가 필요하지 않음
    1. 해당 [Therorem 1.]은 (Eq. 10)의 parameter를 가지는 (Eq. 11)의 reverse SDE solver의 optimality를 discrete path $X=\{X_{kh}\}_{k=0}^{N}$의 likelihood 측면에서 확립하고,
    2. (Eq. 6-R)의 continuous model에 대한 continuous path $\{X_{t}\}_{t\in[0,1]}$ optimality는 parameter $\theta=\theta^{*}$로 보장함
  • [Theorem 1.]의 reverse SDE solver는 time $t$에서 increment가 $\hat{X}_{t}, s_{\theta}(\hat{X}_{t},t)$의 linear combination이고, 평균 0과 diagonal isotropic covariance matrix를 가지는 Gaussian noise로 구성된 모든 fixed-step solver를 포함함
    • $\hat{\kappa}\equiv 0,\hat{\omega}_{t,h}\equiv 0,\hat{\sigma}_{t,h}\equiv\sqrt{\beta_{t}h}$의 특수한 경우, Euler-Maruyama solver가 포함될 수 있음
    • Fixed $t$와 $h\rightarrow 0$의 경우, $\kappa_{t,h}^{*}=\bar{o}(1),\omega_{t,h}^{*}=\bar{o}(1),\sigma_{t,h}^{*}=\sqrt{\beta_{t}h}(1+\bar{o}(1)$을 가짐
    • 따라서 optimal SDE solver는 $N$이 작거나 $t$가 $h$와 동일한 order일 때, general-purpose Euler-Maruyama solver와 달라짐
      - 즉, DPM inference의 final step에 해당
  • 추가적으로 [Theorem 1.]의 (2)는 (1)의 결과를 strengthen 한 것이지만, mel-spectrogram inversion과 같은 strong condition을 사용하여 생성하는 경우, data distribution에 대한 가정이 viable 해짐
    - e.g.) DiffVC가 random variable $X_{0}$와 injective function $\psi$에 대해 $c=\psi(X_{0})$로 condition 된 경우

4. Experiments

- Settings

• Dataset : VCTK, LibriTTS
• Comparisons : AGAIN-VC, FragmentVC, VQMIVC, BNE-PPG-VC
• SDE Solver
  • 먼저 논문은 sampling 과정에서 다음의 SDE solver를 고려함:
    (Eq. 12) $\hat{X}_{t-h}=\hat{X}_{t}+\beta_{t}h\left(\left(\frac{1}{2}+\hat{\omega}_{t,h} \right)(\hat{X}_{t}-\bar{X})+(1+\hat{\kappa}_{t,h})s_{\theta}(\hat{X}_{t},\bar{X},g_{t}(Y),t)\right)+\hat{\sigma}_{t,h}\xi_{t}$
    - $t=1, 1-h,...,h$이고 $\xi_{t}$는 $\mathcal{N}(0,I)$의 $i.i.d.$ sample
  • $\hat{\kappa}_{t,h}=\kappa^{*}_{t,h},\hat{\omega}_{t,h}=\omega_{t,h}^{*}, \hat{\sigma}_{t,h}=\sigma_{t,h}^{*}$의 경우 MR-VP DPM에 대한 maximum likelihood reverse SDE solver가 됨
    - $\kappa_{t,h}^{*}, \omega_{t,h}^{*}, \sigma_{t,h}^{*}$ : (Eq. 10) 참고
  • 한편으로 conditional distribution $\text{Law}(X_{0}|X_{t})$의 variance를 추정하는 것은 trivial 하지 않음
    - 이때 $g_{t}(Y)$에 대한 strong conditioning으로 인해 해당 variance가 작다고 가정하여 $\sigma_{t,h}^{*}$에 대한 term을 skip 한 다음,
    - $\hat{\sigma}_{t,h}=\sigma_{t-h,t}$만을 사용하면 ML-$N$ sampling method를 얻을 수 있음 ($N=1/h$ : SDE solver step 수)
  • 추가적으로 Euler-Maruyama solver (EM-$N$)과 Probability Flow Sampling (PF-$N$)을 비교
    - EM-N에서 $\hat{\kappa}_{t,h}=0,\hat{\omega}_{t,h}=0,\hat{\sigma}_{t,h}=\sqrt{\beta_{t}h}$
    - PF-N에서 $\hat{\kappa}_{t,h}=-0.5, \hat{\omega}_{t,h}=0,\hat{\sigma}_{t,h}=0$

- Results

• Speaker Conditioning Analysis
  • 각 input type에 대해 speaker conditioning network $g_{t}(Y)$를 training 하여 비교해 보면
  • VCTK,  LibriTTS 모두에서 $wodyn$이 최고의 성능을 보임
    - 즉, time $t$에서 speaker embedding을 noisy target mel-spectrogram $Y_{t}$와 함께 decoder에 conditioning 해야 함
  • $Y_{t}$에 대한 conditioning은 noisy target이 어떻게 sound 되는지에 대한 diffusion-specific information을 제공하지만, pre-trained speaker verification network의 embedding은 clean target만 포함하기 때문

Speaker Conditioning 비교

• Any-to-Any Voice Conversion
  • 전체적인 naturalness, similarity 측면에서도 DiffVC가 가장 우수한 성능을 보임

전체 성능 비교

• Large scale dataset에 대해서도 DiffVC의 성능이 가장 뛰어남

Large Scale Dataset에서의 성능 비교

• Maximum Likelihood Sampling
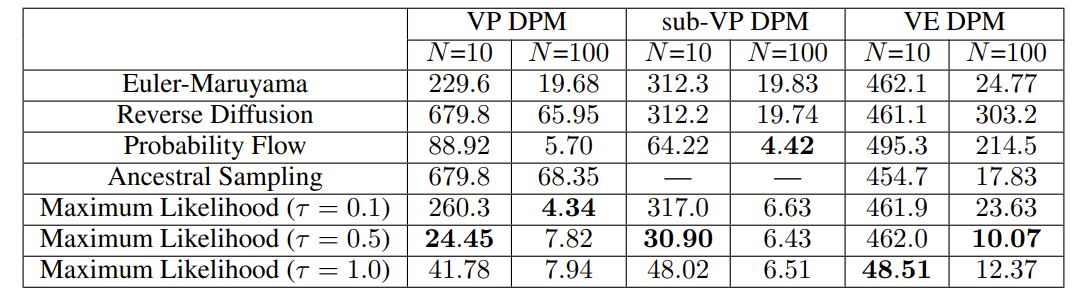
  • CIFAR-10 image generation task에 대해 Frechet Inception Distance (FID) 측면에서 여러 DPM을 비교해 보면
  • Likelihood와 FID는 전혀 correlate 되어 있지 않은 metric임에도 불구하고, 대부분의 경우에서 maximum likelihood SDE solver가 가장 좋은 FID 성능을 보임
    - 특히 hyperparameter $\tau$를 adjust 하여 더 나은 성능을 얻을 수도 있음

SDE Solver 비교

• 추가적으로 각 sampling method에 대해 10 reverse diffusion setp에서 생성된 image들은 아래와 같음
  - 왼쪽에서부터 각각 Euler-Maruyama, Probability Flow, Maximum Likelihood ($\tau=0.5$), Maximum Likelihood ($\tau=1.0$)

생성된 Image 비교