[Paper 리뷰] VQVC+: One-Shot Voice Conversion by Vector Quantization and U-Net Architecture

VQVC+: One-Shot Voice Conversion by Vector Quantization and U-Net Architecture

---

• AutoEncoder-based voice conversion은 speaker identity와 input speech content를 disentangle 하여 unseen speaker에 대해 generalize 됨
  - BUT, imperfect disentanglement로 인해 합성 품질의 한계가 있음
• VQVC+
  • AutoEncoder-based system에 대해 U-Net architecture를 도입해 conversion 품질을 향상
  • Strong information bottleneck을 위해 latent vector를 quantize 하는 vector quantization을 도입
• 논문 (INTERSPEECH 2020) : Paper Link

---

1. Introduction

• Voice Conversion (VC)는 source speech의 linguistic information을 유지하면서 target speaker의 voice로 변환하는 것을 목표로 함
  • 이때 target speaker를 imitate 하기 위해 VC system은 source speaker의 tone, accent, vocalization을 modify 할 수 있어야 함
    1. 이를 위해 Generative Adversarial Network (GAN) 기반의 StarGAN-VC, CycleGAN-VC나 Blow와 같은 flow-based model을 활용할 수 있음
    2. 한편으로 embedding space에서 speaker unit과 content unit을 disentangle 하여 conversion을 수행할 수도 있음
       - 대표적으로 AutoVC는 pre-trained speaker encoder를 통해 latent representation을 추출
       - AdaIN-VC는 AdaIN을 활용하여 다른 speaker에 mapping 하는 방식을 활용
       - VQVC의 경우 vector quantization을 활용하여 speaker information을 반영
  • 특히 disentangle-based VC는 unseen speaker에 대한 합성이 쉽고, 추론 과정에서 one-shot VC가 가능하다는 장점이 있음
    - BUT, latent space를 disentangle 하는 strong bottleneck이 필요하고 constraint로 인해 합성 품질이 제한적임

-> 그래서 disentanlge-based VC의 합성 품질을 더욱 개선한 VQVC+를 제안

 

• VQVC+
  • Vector Quantization (VQ)와 Instance Normalization (IN)을 결합한 U-Net architecture를 활용
  • VQ의 strong information bottleneck을 통해 U-Net이 reconstruction 과정에서 overfitting 되는 것을 방지

< Overall of VQVC+ >

• U-Net architecture와 VQ를 결합한 voice conversion model
• 결과적으로 기존보다 뛰어난 합성 품질을 달성

2. Method

- VQVC

• VQVC는 self-reconstruction loss를 포함한 one-shot VC system으로, content information을 discrete code로 represent 하고 speaker information은 continuous representation과 discrete code 간의 차이로 취급함
  • 이를 위해 아래 그림과 같은 AutoEncoder architecture를 활용
    1. $\mathcal{X}$를 전체 training set, $\mathbf{X}=\{x_{0},x_{1},...,x_{T}\}$를 acoustic feature의 sequence로 represent 되는 audio segment $\mathbf{X}\in\mathcal{X}$라고 하자
       - $T$ : audio duration, $\text{enc}$ : encoder, $\text{dec}$ : decoder
       - $\mathcal{Q}$ : quantization codebook, $\text{Quantize}$ : quantization function
    2. 그러면 audio segment $\mathbf{X}$가 주어졌을 때, continuous latent representation $\mathbf{V}\in\mathbb{R}^{F\times T}$, content embedding $\mathbf{C}\in\mathbb{R}^{F\times T}$, speaker embedding $\mathbf{S}\in\mathbb{R}^{F\times T}$는:
       (Eq. 1) $\mathbf{V}=\text{enc}(\mathbf{X}),\,\,\, \mathbf{C}=\text{Quantize}(\mathbf{V}),\,\,\, s=\mathbb{E}_{t}[\mathbf{V}-\mathbf{C}],\,\,\, \mathbf{S}=\{ \underset{T\,\,\text{times}}{\underbrace{s,s,...,s}}\}$
       $\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \text{Quantize}(\mathbf{V})=\{q_{0},q_{1},...,q_{T}\},\,\,\, q_{j}=\arg\min_{q\in\mathcal{Q}}(|| v_{j}-q||_{2}^{2})$
       - $F$ : embedding size, vector $v_{j}$의 dimension은 $\mathcal{Q}$의 code dimension과 동일
  • Instance Normalization (IN)는 quantization 이전에 추가되고, speaker information은 global information으로 취급됨
    1. 따라서 $\mathbf{V}$에서 $\mathbf{C}$를 빼서 $s$를 얻은 다음, audio segment의 global information을 나타내는 utterance duration에 대한 기댓값 $\mathbb{E}_{t}$를 계산함
    2. 이후 $s$를 $T$번 repeating 하여 $\mathbf{S}$를 얻고, concatenate하여 $\mathbf{C}, \mathbf{S}$의 dimension을 일치시킴
    3. 최종적으로 $\mathbf{S}$를 $\mathbf{C}$에 추가하고 decoder를 통해 reconstruction을 수행함:
       (Eq. 2) $\hat{\mathbf{X}}=\text{dec}(\mathbf{C}+\mathbf{S})$
  • Training phase에서 reconsturction loss는:
    (Eq. 3) $\mathcal{L}_{rec}(\mathcal{Q},\theta_{enc},\theta_{dec})=\mathbb{E}_{\mathbf{X}\in \mathcal{X}}[||\hat{\mathbf{X}}-\mathbf{X} ||_{1}^{1}]$
  • 추가적으로 latent loss $\mathcal{L}_{latent}$를 통해 discrete code와 continuous embedding 간의 distance를 최소화함:
    (Eq. 4) $\mathcal{L}_{latent}(\theta_{enc})=\mathbb{E}_{t}[|| \text{IN}(\mathbf{V})-\mathbf{C}||_{2}^{2}]$
    - $\text{IN}$ : instance normalization layer
  • 결과적으로 얻어지는 VQVC의 final loss는:
    (Eq. 5) $\mathcal{L}=\mathcal{L}_{rec}+\lambda\mathcal{L}_{latent}$
    - 추론 시, content embedding $\mathbf{C}$와 speaker embedding $\mathbf{S}$는 서로 다른 speaker에서 추출됨

VQVC Architecture

- VQVC+

• 기존의 VQVC는 linguistic content와 speaker information을 well-disentangle 할 수 있지만, 합성 품질에서 한계가 있음
  • Vector quantization 과정에서 information loss가 발생하여 decoder가 content를 적절하게 reconstruct 할 수 없기 때문
  • 따라서 VQVC+에서는 U-Net architecture를 도입하여 기존 VQVC의 합성 품질을 개선함
    1. Encoder는 3개의 VQ Down-Conv module로 구성되고, decoder는 3개의 VQ Up-Conv module로 구성됨
    2. 이때 decoder layer에서 receive 한 content information을 strength 하기 위해 content embedding $\mathbf{C}$와 speaker embedding $\mathbf{S}$는 U-Net과 같이 해당 decoder layer로 skip-connect 됨

VQVC+ Architecture

• VQ Down-Conv Module
  • VQ Down-Conv는 2개의 $3\times 1$ kernel 1D Convolutional layer, IN layer, vector quantization layer로 구성됨
    - $\mathrm{Conv1d\text{-}c_{1}\text{-}c_{2}\text{-}N}$ : 1D convolution layer, $c_{1},c_{2}$ : 각각 input/output channel, $N$ : stride
  • $\mathrm{VQ\,down\text{-}conv(c_{in},c_{h})}$는 dimension이 $(c_{in},T)$인 matrix를 input으로 하고 $\mathbf{V},\mathbf{C},\mathbf{S}$를 output 함
    1. $\mathbf{V}$는 convolution block에서 얻어지는 continuous space embedding이고 $\mathbf{C}$는 IN, VQ로 얻어지는 $\mathbf{V}$의 quantized matrix, $\mathbf{S}$는 (Eq. 1)의 speaker embedding을 의미
    2. $\mathbf{V},\mathbf{C},\mathbf{S}$의 dimension은 각각 $(c_{in}/2,T/2),(c_{in}/2,T/2),(c_{in}/2,T/2)$

VQ Down-Conv Module

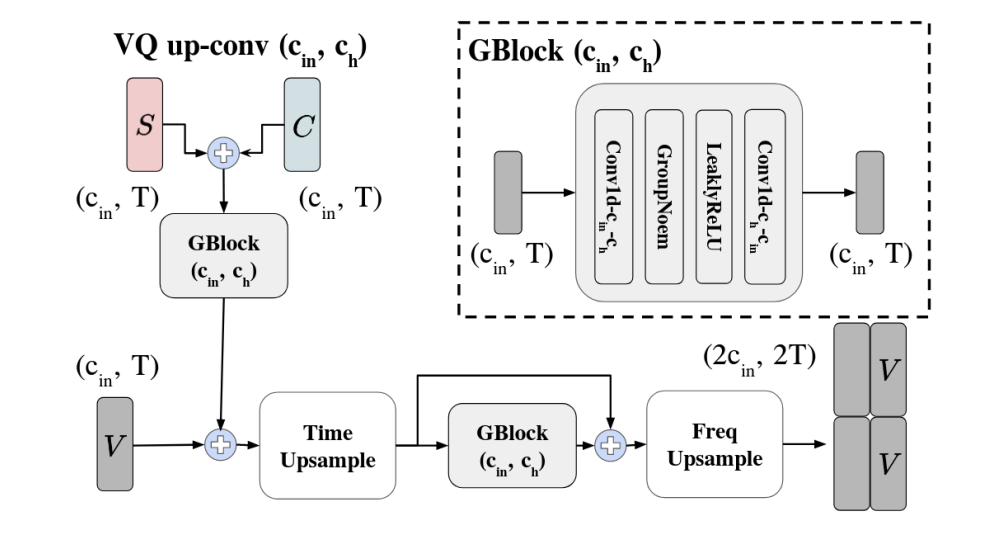
• VQ Up-Conv Module
  • VQ Up-Conv는 앞선 layer의 output인 $\mathbf{V}$와 해당 encoder layer에서 생성된 $\mathbf{C},\mathbf{S}$를 input으로 사용함
    - 이때 embedding은 time, frequency domain 모두에서 2배로 upsampling 됨
  • 구조적으로 VQ Up-Conv는 Group Norm Block (GBlock), TimeUpsampling, FreqUpsampling으로 구성됨
    1. GBlock은 2개의 $3\times 1$ kernel 1D convolution layer, Leaky ReLU, Group Norm으로 구성됨
    2. TimeUpsampling module은 각 vector를 두배로 duplicate 하여 time dimension을 expand 함
    3. FreqUpsampling module은 mel-spectrogram에서 low-frequency part를 통해 high-frequency part를 생성하고 concatenate 하여 output 함
  • 전체적으로 $\mathbf{C},\mathbf{S}$를 add하여 GBlock에 전달한 다음, $\mathbf{V}$를 추가함
    - 최종적으로 2개의 upsampling module을 통과하여 output을 얻음

VQ Up-Conv Module

• U-Net
  • VQVC+는 U-Net architecture를 기반으로 구성됨
    1. 먼저 각 VQ Down-Conv module은 자체적으로 $\mathbf{V}, \mathbf{C},\mathbf{S}$를 생성하고
    2. 이후 $\mathbf{V}$는 다음 VQ Down-Conv module을 통과하고 $\mathbf{C}, \mathbf{S}$는 decoder의 VQ Up-Conv module을 통과함
  • VQVC+는 각 layer의 latent loss $\mathcal{L}_{latent}$와 reconstruction loss $\mathcal{L}_{rec}$로 training 됨
    - 여기서 모든 layer의 latent loss $\mathcal{L}_{latent}$에 대해, (Eq. 5)와 동일한 weight $\lambda$를 적용함

Upsampling Block

3. Experiments

- Settings

• Dataset : VCTK
• Comparisons : AutoVC, AdaIN-VC

- Results

• Content Embedding
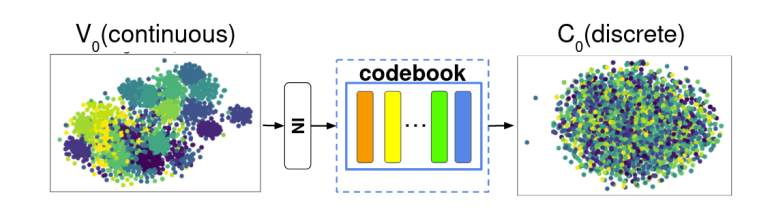
  • IN과 VQ의 효과를 확인하기 위해 서로 다른 speaker에 대해 t-SNE를 적용하면
  • $\mathbf{V}_{0}$는 clustering 되어 나타나지만 $\mathbf{C}_{0}$에서는 명확한 group이 나타나지 않음

t-SNE 결과

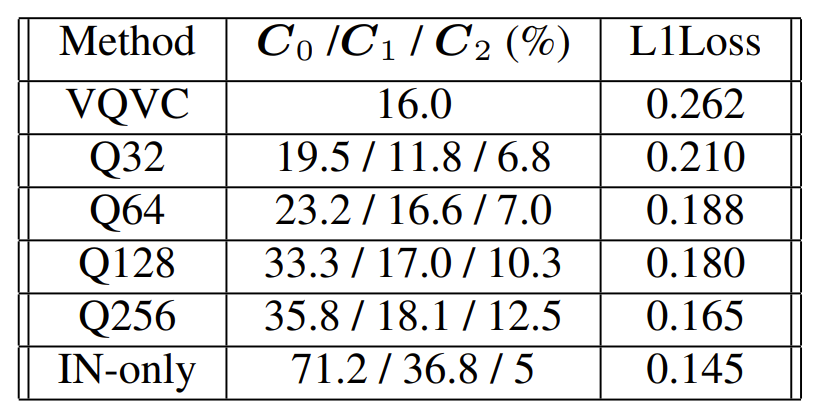
• Encoder layer $\mathbf{C}_{0}, \mathbf{C}_{1}, \mathbf{C}_{2}$를 비교해 보면, layer가 깊어질수록 낮은 accuracy를 보임
  • 특히 IN-only model은 $\mathbf{C}_{0}$에서 71.2%의 speaker identification rate를 보임
    - 즉, IN-only model은 content와 speaker information을 disentangle 하는 ability가 없고 단순히 source audio를 reconstruct 함
  • Codebook size의 경우 information bottleneck의 강도를 결정함
    - Q32와 같은 smaller codebook은 낮은 speaker identification rate를 달성할 수 있지만 reconstruction error를 일으킬 수 있음
    - Q256과 같은 larger codebook은 reconstruction에는 효과적이지만 speaker information이 quantized code로 leak 될 수 있음

Speaker Identification Rate 비교

• Speaker Embedding
  • $\mathbf{S}_{0}, \mathbf{S}_{1}, \mathbf{S}_{2}$에 대해 classifier의 accuracy를 비교해 보면
  • $\mathbf{S}_{1}, \mathbf{S}_{2}$의 accuracy는 각각 72.2%, 45.4%로 lower resolution space에서 speaker embedding을 추출하는 것으로 나타남

Speaker Embedding에 대한 Identifying Accuracy 비교

• Subjective Evaluations
  • MOS 측면에서 VQVC+는 unseen (-U), seen (-S) 모두에서 가장 우수한 성능을 달성함

MOS 비교

• Pairwise test 측면에서도 VQVC+가 가장 선호됨

Pairwise Comparison