[Paper 리뷰] MIDI-Voice: Expressive Zero-Shot Singing Voice Synthesis via MIDI-Driven Priors

MIDI-Voice: Expressive Zero-Shot Singing Voice Synthesis via MIDI-Driven Priors

---

• 기존의 Singing Voice Synthesis 모델은 unseen speaker와 fundamental frequency를 부정확하게 예측하므로 낮은 합성 품질을 보임
• MIDI-Voice
  • 더 나은 singing voice style adaptation을 위해 MIDI-based prior를 score-based diffusion model에 적용
  • 특히 MIDI-driven prior를 생성하여 note information을 반영하고 고품질의 style adaptation을 지원
  • 추가적으로 expressive synthesis를 위해 DDSP-based MIDI-style prior를 구성
• 논문 (ICASSP 2024) : Paper Link

---

1. Introduction

• Singing Voice Synthesis (SVS)는 musical score로부터 expressive, natural singing voice를 합성하는 것을 목표로 함
  • 일반적인 two-stage SVS 모델은 note, lyrics, speaker ID를 input으로 mel-spectrogram을 생성하는 acoustic model과 합성된 mel-spectrogram을 waveform으로 변환하는 vocoder로 구성됨
  • 한편으로 합성 품질을 향상하기 위해 Generative Adversarial Network (GAN)나 diffusion-based 모델을 고려할 수 있음
    - 이때 고품질의 합성을 위해서는 정확한 prior distribution을 생성할 수 있어야 함
    - e.g.) diffusion-based SVS 모델의 경우 Gaussian distribution 대신 data-driven prior를 활용
  • 한편으로 Fundamental frequency $F0$ 모델링 역시 SVS 작업에서 상당히 중요함
    1. Singing voice의 expressiveness는 $F0$의 primary component인 baseline, microprosody, vibrato와 밀접하게 관련되어 있기 때문
       - 이를 위해 Text-to-Speech (TTS)의 $F0$ prediction method를 활용할 수 있지만, SVS에서의 $F0$ 예측에는 여전히 한계가 있음
    2. 특히 $F0$를 explicit 하게 예측하지 않는 경우, unseen speaker에 대해 부정확한 singing melody를 생성하게 됨
       - 따라서 zero-shot SVS는 추론 단계에서 ground-truth pitch를 singing voice conversion을 위해 사용함
       - BUT, 해당 ground-truth $F0$를 사용하더라도 data-driven prior로 인해 부정확한 $F0$를 생성할 수 있음

-> 그래서 고품질의 zero-shot SVS를 위한 score-based diffusion SVS 모델인 MIDI-Voice를 제안

 

• MIDI-Voice
  • 기존의 data-driven prior 대신 Musical Instrument Digital Interface (MIDI)-based prior를 사용하여 singing voice Mel-spectrogram을 생성
    - 이를 통해 부정확한 $F0$로 인한 SVS 품질 저하를 방지할 수 있음
  • 추가적으로 singing style adaptation을 지원하는 additional information을 반영한 MIDI-style prior를 얻기 위해 Differentiable Digital Signal Processing (DDSP)을 채택
  • 결과적으로 MIDI-based prior는 speaker information이 아닌 note information 만을 반영하므로 robust 한 zero-shot SVS가 가능함

< Overall of MIDI-Voice >

• Zero-shot SVS를 위해 MIDI-based prior를 diffusion model에 도입
• DDSP를 사용하여 MIDI-style prior에 더 나은 singing voice style transfer 능력을 반영
• 결과적으로 기존 방식들보다 뛰어난 zero-shot SVS 성능을 달성

2. Method

• Zero-shot SVS는 target speaker와 musical score에 adapting 하여 고품질의 singing voice를 생성하는 것을 목표로 함
  - 이때 MIDI-Voice는 style encoder, condition encoder, prior generator, diffusion-based Mel decoder로 구성됨

Overall of MIDI-Voice

- Style Encoder

• Zero-shot SVS를 위해 Meta-StyleSpeech의 style encoder를 사용하여 style vector $\omega$를 추출함
  • Style encoder는 spectral/temporal processor, multi-head attention과 temporal average pooling이 있는 transformer layer로 구성됨
    - 결과적으로 style encoder는 reference mel-spectrogram을 input으로 하여 style vector를 output 함
  • 이때 single speaker는 전체 노래에 대해 동일한 singing style을 유지하지 않으므로, training 중에 동일한 speaker의 다른 singing voice에서 reference mel-spectrogram을 random sampling 함
    - 이를 통해 style encoder가 단순히 reference mel-spectrogram을 기반으로 singing style을 변경하지 않도록 보장

- Condition Encoder

• Condition encoder는 text encoder, note encoder, auxiliary encoder의 3가지 encoder로 구성됨 
  • 먼저 text encoder는 lyrics의 phoneme으로부터 linguistic representation을 추출 
  • Note encoder는 phoneme-level note pitch sequence에서 pitch representation을 추출한 다음, length regulating operation 이전에 두 phoneme-level representation을 추가함
    - 이때 musical score로부터 duration이 이미 결정되어 있으므로 target singing voice의 duration으로 representation을 expand 할 수 있음
  • Auxiliary encoder는 extended representation과 $\omega$로부터 condition representation $h_{cond}$를 encoding 함 
    1. 여기서 diffusion-based Mel decoder의 condition으로 해당 condition representation을 사용
    2. 더 정확한 pronunciation과 pitch information을 포함하는 condition representation을 얻기 위해, 다음의 condition loss $\mathcal{L}_{c}$를 추가함:
       (Eq. 1) $\mathcal{L}_{c}=\sum_{i=0}^{T}(h_{cond}-Y)^{2}$
       - $Y$ : target mel-spectrogram

Prior Generation Pipeline

- Diffusion Modelling

• Diffusion model은 Markov chain을 사용하여 Gaussian distribution $\mathcal{N}(0,I)$에 의해 생성된 prior noise distribution을 점진적으로 denoise 하는 방식
  • 특히 score-based diffusion의 경우 해당 denoising process에 Stochastic Differential Equation (SDE)를 도입함
    - 이때 score-based model은 Gaussian noise를 기반으로 한 prior noise distribution 대신에 data-driven prior로부터 sample을 생성할 수 있음
  • 한편으로 MIDI-Voice는 data-driven prior 대신 MIDI-based prior를 사용하는 score-based diffusion model을 활용함
• MIDI-driven Prior
  • Zero-shot SVS에서는 prior distribution의 결정이 중요하므로, speaker information을 포함하지 않는 정확한 pitch information을 통해 MIDI-driven prior를 생성함
    - 해당 MIDI-driven prior를 통해 singing voice representation을 conditioning 하여 style을 adapting 하는 diffusion decoder의 성능을 향상할 수 있음
  • 특히 diffusion model에서 data-driven prior로써 mel-spectrogram을 사용하면 diffusion-based Mel decoder의 adaptation 성능을 저하시킬 수 있음
    - 따라서 MIDI-driven prior는 FluidSynth를 사용하여 MIDI file을 waveform으로 변환한 다음, STFT을 적용하여 생성됨
• MIDI-style Prior
  • MIDI-style prior는 expressive SVS를 위해 desired singing style의 $F0$와 loudness를 사용하여 prior를 생성함
  • MIDI-style prior는 pre-trained DDSP에 대한 input으로 desired singing voice sample에서 추출된 $F0$와 loudness를 사용하여 얻어짐
    - 여기서 training sample에는 reverb가 포함되지 않으므로 DDSP에서 room reverberation은 제거됨
  • 결과적으로 instrumental sound를 포함하여 생성되는 MIDI-style prior에는 기존의 MIDI-driven prior 보다 더 expressive 한 style이 반영됨
• Forward Diffusion
  • Forward diffusion process는 Gaussian distribution $\mathcal{N}(0,I)$에서 추출된 noise를 infinite time $T$에 걸쳐 점진적으로 data에 inject 하는 과정
    • 따라서 논문에서는 MIDI-driven piror noise distribution $\mathcal{N}(M_{midi}, I)$에서 noisy sample을 denoise 하는 것을 목표로 함:
      (Eq. 2) $dY_{t}=\frac{1}{2}(M_{midi}-Y_{t})\beta_{t}dt+\sqrt{\beta_{t}}dW_{t},\,\,\,t\in[0,T]$
      - $M_{midi}$ : MIDI-driven prior / MIDI-style prior, $t$ : continuous time step
      - $\beta$ : noise scheduling function, $W_{t}$ : standard Brownian motion
    • 그러면 (Eq. 2)의 solution은:
      (Eq. 3) $Y_{t}=(I-e^{-\frac{1}{2}\int_{0}^{t}\beta_{s}ds})M_{midi}+e^{-\frac{1}{2}\int_{0}^{t}\beta_{s}ds}Y_{0}+\int_{0}^{t}\sqrt{\beta_{s}}-e^{-\frac{1}{2}\int_{s}^{t}\beta_{u}du}dW_{s}$
    • Ito's integral에 따라, transition density $p(Y_{t}|Y_{0})$는 다음의 Gaussian distribution $\lambda(I,t)$와 같음:
      (Eq. 4) $p(Y_{t}|Y_{0})=(I-e^{-\frac{1}{2}\int_{0}^{t}\beta_{s}ds})M_{midi}+e^{-\frac{1}{2}\int_{0}^{t}\beta_{s}ds}Y_{0},\,\,\, \lambda (I,T)=I-e^{-\frac{1}{2}\int_{0}^{t}\beta_{s}ds}$
  • 따라서 $Y_{t}$는 $Y_{0}$에 관계없이 $\mathcal{N}(M_{midi},I)$으로 수렴하고, SDE는 data distribution을 $\mathcal{N}(M_{midi},I)$로 변환함 
• Reverse Diffusion
  • Reverse diffusion process는 noise에서 data sample까지 점진적으로 denoising을 수행하는 것
    1. 여기서 reverse diffusion에 대한 SDE는:
       (Eq. 5) $dY_{t}=\frac{1}{2}\left( (M_{midi}-Y_{t})-\nabla\log p_{t}(Y_{t}) \right)\beta_{t}dt+\sqrt{\beta_{t}}d\tilde{W}_{t}$
       - $p_{t}$ : random variable $Y_{t}$의 probability density function
       - $\tilde{W}_{t}$ : reverse Brownian motion
    2. 한편으로 다음의 ordinary differential equation을 고려할 수도 있음:
       (Eq. 6) $dY_{t}=\frac{1}{2}\left( (M_{midi}-Y_{t})-\nabla\log p_{t}(Y_{t}) \right)\beta_{t}dt, \,\,\, t\in[0,T]$
  • 결과적으로 SDE를 사용하여 $Y_{t}$에서 $Y_{0}$를 생성할 수 있음
    - 즉, MIDI-Voice는 $\mathcal{N}(M_{midi},I)$에서 sampling 된 $Y_{t}$로부터 $Y_{0}$를 생성함

- Training

• MIDI-Voice는 noisy data의 log-density에 해당하는 estimated gradient에 대한 기댓값을 계산함
  • 여기서 time $t$까지 accumulate 된 noise로 corrupt 된 data $Y_{0}$의 log-density gradient를 추정하는 loss function은:
    (Eq. 7) $\mathcal{L}_{diff}=\mathbb{E}_{\epsilon_{t}}\left[|| s_{\theta}(Y_{t},M_{midi},h_{cond},\omega,t)+\lambda(I,t)^{-1}\epsilon_{t} ||\right]$
    - $\omega$ : style vector, $\epsilon_{t} \in \mathcal{N}(0,\lambda(I,t))$
    - $s_{\theta}$ : noise estimation network
  • 최종적으로 MIDI-Voice는 noise estimator와 condition encoder를 jointly optimize 함:
    (Eq. 8) $\mathcal{L}=\mathcal{L}_{diff}+\mathcal{L}_{c}$
    - $\mathcal{L}_{diff}$ : (Eq. 7)의 diffusion loss, $\mathcal{L}_{c}$ : (Eq. 1)의 condition encoder loss 

3. Experiments

- Settings

• Dataset : Guide Vocal Dataset
• Comparisons : VISinger, Grad-TTS

- Results

• 먼저 seen speaker에 대한 결과를 확인해 보면, MIDI-Voice가 가장 뛰어난 합성 성능을 보임
  - 특히 data-driven prior 대신 MIDI-based prior를 사용하는 경우 diffusion model의 성능이 크게 향상됨

Seen Speaker에 대한 성능 비교

• Unseen speaker에 대한 zero-shot test의 경우에 대해서도 MIDI-Voice의 성능이 가장 뛰어남
  - 이때 MIDI-Voice는 unseen speaker의 $F0$를 정확하게 반영할 수 있음

Unseen Speaker에 대한 Zero-Shot Test 결과

• Ablation study 측면에서
  • Data-driven prior는 unseen speaker의 style을 반영하는 능력이 떨어지지만, MIDI-based prior는 note information이 포함되므로 zero-shot SVS에 대한 diffusion model의 adaptation을 향상할 수 있음
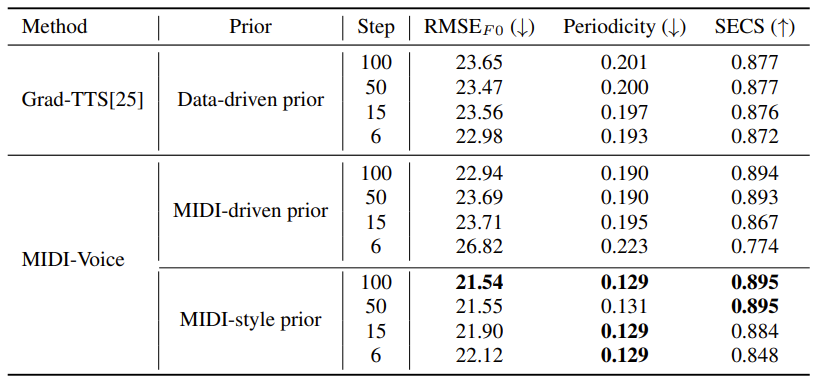
  • Diffusion process의 iteration step에 따른 adaptation 성능을 비교해 보면
    1. Iteration step을 증가시키더라도 data-driven prior에는 이미 많은 양의 data가 포함되어 있기 때문에 adaptation의 한계가 있음
    2. 반면 MIDI-driven prior는 iteration step을 증가시켰을 때, adaptation 성능을 향상할 수 있음

Iteration Step에 따른 성능 비교