[Paper 리뷰] NaturalSpeech: End-to-End Text-to-Speech Synthesis with Human-Level Quality

NaturalSpeech: End-to-End Text-to-Speech Synthesis with Human-Level Quality

---

• Text-to-Speech에서 human-level quality를 판단하는 것은 어려움
• NaturalSpeech
  • Human-level quality를 달성하기 위해 variational auto-encoder를 활용한 end-to-end text-to-speech 모델
  • Phoneme pre-training, differentiable duration modeling, bidirectional prior/posterior modeling, VAE memory mechanism을 포함
• 논문 (PAMI 2024) : Paper Link

---

1. Introduction

• Text-to-Speech (TTS)는 text로부터 intelligible, natural speech를 합성하는 것을 목표로 함
  • 특히 기존의 TTS 모델들은 높은 합성 품질에도 불구하고, human recording과 비교하면 여전히 품질의 차이가 존재함
    - BUT, TTS에서 human-level quality에 대한 formal definition은 아직 제시되지 않음
  • 한편으로 TTS에서 human-level quality를 달성하기 위해서는 다음의 문제를 해결해야 함
    1. Reduce training-inference mismatch
       - Grad-TTS, Glow-TTS와 같은 cacaded pipeline은 mel-spectrogram과 duration에 대한 mismatch로 인해 성능의 한계가 있음
       - 이때 end-to-end pipeline를 통해 training-inference mismatch 문제를 완화 가능
    2. Alleviate one-to-many mapping
       - 하나의 text sequence는 $F0$, duration, prosody 등의 다양한 variation information을 포함하고 있음
       - 이때 FastSpeech2와 같이 variance adaptor 만을 사용하는 것으로는 one-to-many mapping 문제를 완전히 해결할 수 없음
       - 따라서 posterior의 complexity를 줄이고 prior를 향상할 수 있는 방법이 필요함
    3. Improve representation capacity
       - TTS 모델은 phoneme sequence에서 representation을 효과적으로 추출하고 speech의 복잡한 data distribution을 학습할 수 있어야 함
       - Large-scale phoneme pre-training, powerful generative model을 통해 더 나은 text representation과 speech distribution을 학습할 수 있음

-> 그래서 TTS에 대한 위 문제들을 해결하고, 실질적인 human-level quality를 달성하는 NaturalSpeech를 제안

 

• NaturalSpeech
  • Human-level quality를 달성하는 fully end-to-end TTS 모델
  • Variational AutoEncoder (VAE)를 활용하여 high-dimensional speech $x$를 continuous frame-level representation인 posterior $q(z|x)$로 compress 한 다음, waveform $p(x|z)$를 reconstruct 함
    - 이때 해당하는 prior $p(z|y)$는 text sequence $y$로부터 얻어짐
  • $p(z|y)\rightarrow p(x|z)$를 통해 TTS를 수행할 때, speech의 posterior가 text의 prior보다 복잡하므로 prior/posterior를 효과적으로 match 하기 위해 다음의 방식을 도입함:
    
    1. Phoneme sequence에서 better representation을 추출하기 위해 phoneme encoder에 대한 large-scale pre-training을 적용
    2. Duration predictor와 upsampling layer로 구성된 fully differentiable durator를 통해 duration modeling을 개선

< Overall of NaturalSpeech >

• Subjective measure의 통계적 유의성을 기반으로 human-level quality를 정의
• Phoneme pre-training, differentiable duration modeling, bidirectional prior/posterior modeling, VAE memory mechanism을 포함한 VAE 기반의 end-to-end TTS 모델
• 결과적으로 다른 TTS 모델과 비교하여 실질적인 human-level quality를 달성

2. Definition and Judgment of Human-Level Quality in TTS

- Definition of Human-Level Quality

• 논문에서는 human-level quality를 다음과 같이 정의함:
  • [Definition 1]
    TTS system에서 생성된 음성의 quality score와 test set에서 해당하는 human recording의 quality score가 통계적으로 유의하지 않은 경우, 해당 TTS system은 test set에서 human-level quality를 달성한다.
  • 즉, TTS의 output이 human recording과 통계적으로 indistinguishable 한 경우, human-level quality라고 볼 수 있음

- Judgment of Human-Level Quality

• Judgment Guideline
  • 합성된 음성과 human recording 간의 품질 차이를 측정하는 PESQ, STOI, SI-SDR 등의 objective metric이 존재하지만, perception quality에 대해서는 reliable 하지 않음
  • 따라서 논문은 subjective evaluation을 기반으로 human-level quality를 측정함 
    1. 이를 위해 $(-3, 3)$ range의 7 point를 가지는 Comparative Mean Opinion Score (CMOS)를 활용
       
    2. 이후 CMOS 측면에서 두 system의 차이를 측정하기 위해 Wilcoxon Signed-Rank Test를 수행
  • 결과적으로 TTS system에 의해 생성된 음성이 평균 CMOS가 0에 가깝고 Wilcoxon Signed-Rank Test의 $p$-level이 $p>0.05$를 만족하는 경우, human-level quality라고 함 

Human Recording에 대한 기존 TTS 모델 성능 비교

• Judgment of Previous TTS Systems
  • 실제로 기존 TTS 모델인 FastSpeech2, Glow-TTS, Grad-TTS, VITS에 대한 human-level quality를 측정해 보면, 모두 위 표와 같이 높은 MOS에 비해 human recording과는 실질적으로 큰 차이를 보임
  • 이때 아래 표와 같이 FastSpeech2를 기반으로 HiFi-GAN vocoder를 적용한 TTS system을 분석해 보면:
    1. Vocoder의 ground-truth mel-spectrogram과 Mel-Decoder의 예측 mel-spectrogram 간의 mismatch
    2. Variance Adaptor의 다양한 variation information 반영 부족
    3. Phoneme encoder의 복잡한 speech data distribution 모델링 한계로 인해 human-level quality를 달성할 수 없음

각 module별 CMOS 비교

3. Description of NaturalSpeech System

• NaturalSpeech는 human recording과 합성된 speech 간의 quality gap을 줄이기 위해 fully end-to-end TTS 모델로 구성됨

- Design Principle

• NaturalSpeech는 VAE를 활용하여 high-dimensional speech $x$를 posterior distribution $q(z|x)$에서 sampling 되는 frame-level representation $z$로 compress 한 다음, waveform $p(x|z)$를 reconstruct 함
  • 일반적인 VAE formulation에서 prior $p(z)$는 standard isotropic multivariate Gaussian으로 정의됨
    1. 한편으로 TTS input text에서 conditional waveform generation을 수행하기 위해서는 phoneme sequence $y$에서 $z$를 예측해야 함
       - 즉, $z$는 예측된 prior distribution $p(z|y)$에서 sampling 됨
    2. 이를 기반으로 $q(z|x)$와 $p(z|y)$ 모두에서 propagate 되는 gradient를 사용하여 VAE와 prior prediction을 jointly optimize 함
       - 이때 loss function은 evidence lower bound에서 파생되어 waveform reconstruction loss로 사용됨
       - 즉, $\log p(x|z)$ 및 posterior $q(z|x)$와 prior $p(z|y)$간의 Kullback-Leibler divergence loss $\mathrm{KL}[q(z|x)||p(z|y)]$
  • Speech의 posterior가 text의 prior 보다 더 복잡하므로, 논문은 text-waveform을 최대한 가깝게 match 하기 위해 posterior를 단순화하고 prior를 향상하는 여러 module을 도입함
    1. 먼저 phoneme sequence에 대한 masked language modeling을 통해 large-scale text corpus로 phoneme encoder를 pre-training 하여 더 나은 prior prediction를 달성
    2. Posterior는 frame-level이고, phoneme prior는 phoneme-level이므로, length difference를 bridge 하기 위해 differentiable durator를 통해 phoneme prior를 duration에 따라 expand 함
       
    3. Prior를 향상하고 posterior를 단순화하기 위해 bidirectional prior/posterior module을 채택
    4. Waveform reconstruction에 대한 posteriror complexity를 줄이기 위해, Q-K-V attention을 통한 memory bank를 활용하는 memory-based VAE를 도입

Overall of NaturalSpeech

- Phoneme Encoder

• Phoneme Encoder $\theta_{pho}$는 phoneme sequence $y$를 input으로 하여 phoneme hidden sequence를 output 함
  • 이때 논문은 phoneme encoder의 representation capability를 향상하기 위해 large-scale phoneme pre-training을 수행
  • 이를 위해 input으로 phoneme과 sup-phoneme을 모두 사용하는 mixed-phoneme pre-training을 활용
    1. 여기서 masked language modeling을 사용할 때, 일부 sup-phoneme과 해당 phoneme token을 randomly mask 하고 masked phoneme과 sup-phoneme을 동시에 예측함
    2. Mixed-phoneme pre-training 이후, pre-trained model을 활용하여 NaturalSpeech의 phoneme encoder를 initialize 함

NaturalSpeech의 주요 Module

- Differentiable Durator

• Differentiable durator $\theta_{dur}$는 phoneme hidden sequence를 input으로 취하고 frame-level에서 prior distribution sequence를 output 함
  • 여기서 $\theta_{pri} = [\theta_{pho}, \theta_{dur}]$일 때, prior distribution $p(z'|y;\theta_{pho},\theta_{dur}) = p(z'|y;\theta_{pri})$라고 하자
  • 그러면 differentiable durator $\theta_{dur}$는 다음의 module들로 구성됨
    1. 각 phoneme의 duration을 예측하기 위해 phoneme encoder를 기반으로 구축된 duration predictor $\theta_{dp}$
    2. Differentiable way로 phoneme hidden sequence를 frame-level로 expand 하는 projection matrix를 학습하기 위해 predicted duration을 사용하는 learnable upsampling layer $\theta_{lu}$
    3. Prior distribution $p(z'|y;\theta_{pri})$의 평균/분산을 계산하기 위한 2개의 additional linear layer
  • 기존처럼 predicted duration을 사용하여 각 phoneme sequence를 단순히 repeating 하는 것보다, 위와 같이 learnable upsampling layer를 사용하면 각 phoneme에 대해 flexible 한 duration adjustment가 가능함
    - 특히 learnable upsampling layer는 phoneme을 frame expansion differentiable 하게 하므로 NaturalSpeech의 다른 module들과 jointly optimize 될 수 있음
• Differentiable durator의 formulation은 다음과 같음:
  
  1. Duration Predictor
     • 먼저 duration predictor $\theta_{dp}$은 phoneme hidden sequence $\mathbf{H}_{n\times h}$를 input으로 사용하여 output은 estimated phoneme duration $\mathbf{d}_{n\times 1}$를 얻음
       - $n,h$ : 각각 phoneme sequence의 legnth와 hidden dimension size
       
     • Duration predictor $\theta_{dp}$는 ReLU activation, layer normalization, dropout을 포함하는 3개의 1D convolution으로 구성됨
  2. Learnable Upsampling Layer
     • Learnable upsampling layer $\theta_{lu}$는 phoneme duration $\mathbf{d}_{n\times 1}$을 input으로 사용하고, phoneme hidden sequence $\mathbf{H}_{n\times h}$를 frame-level sequence $\mathbf{O}_{m\times h}$로 upsampling 함
       - $m$ : frame 수
     • 이때 duration start/end matrix $\mathbf{S}_{m\times n}, \mathbf{E}_{m\times n}$은:
       (Eq. 1) $S_{i,j}=i-\sum_{k=1}^{j-1}d_{k},\,\, E_{i,j}=\sum_{k=1}^{j}d_{k}-i$
       - $S_{i,j}$ : matrix의 $(i,j)$-th element를 index 함
     • 이후 primary attention matrix $\mathbf{W}_{m\times n\times q}$와 auxiliary context matrix $\mathbf{C}_{m\times n\times p}$를 계산하면:
       (Eq. 2) $\mathbf{W}=\text{Softmax}(\underset{10\rightarrow q}{\text{MLP}}([\mathbf{S},\mathbf{E},\text{Expand}(\text{Conv1D}(\text{proj}(H)))]))$
       (Eq. 3) $\mathbf{C}=\underset{10\rightarrow p}{\text{MLP}}([\mathbf{S},\mathbf{E},\mathrm{Expand}(\mathrm{Conv1D}(\mathrm{Proj}(\mathbf{H})))])$
       - $\text{Proj}(\cdot)$ : input/output dimension이 $h$인 linear layer
       - $\text{Conv1D}(\cdot)$ : layer normalization, Swish activation을 사용한 1D convolution으로 input/output dimension은 각각 $h, 8$로 설정됨
       - $\text{Expand}$ : input matrix를 $m$번 repeating 하여 extra dimension을 추가하는 operation
       - $[\cdot]$ : hidden dimension에 대한 matrix concatenation으로 $10=1+1+8$의 hidden dimension을 얻음
       - $\text{MLP}(\cdot)$ : Swish actiavtion을 사용하는 2-layer fully-connected network- $\text{Softmax}(\cdot)$ : phoneme sequence의 time dimension에서 수행됨
     • Frame-level hidden sequence output $\mathbf{O}_{m\times h}$는 다음으로 얻어짐:
       (Eq. 4) $\mathbf{O}=\underset{qh\rightarrow h}{\text{Proj}}(\mathbf{WH})+\underset{qp\rightarrow h}{\text{Proj}}(\text{Einsum}(\mathbf{W},\mathbf{C}))$
       - $\text{Einsum}(\cdot)$ : einsum operation ($\text{qmn, mnp}\rightarrow \text{qmp}, \mathbf{W}, \mathbf{C}$)
       - 이때 계산을 위해 $\mathbf{W}$를 $m\times n\times q$에서 $q\times m\times n$으로 치환하고, $q\times m\times h$ shape의 $\mathbf{WH}$와 $q\times m\times p$ shape의 $\text{Einsum}(\mathbf{W},\mathbf{C})$를 얻은 다음, 
       - $m\times h$ dimension에 대한 final projection을 위해 각각 $m\times qh, m\times qp$로 reshpae 함
  3. Linear Layers for Mean and Variance
     • $\mathbf{O}_{m\times h}$를 평균/분산 linear layer로 mapping 하여 frame-level prior distribution parameter $\mu(y;\theta_{pri}), \sigma(y;\theta_{pri})$를 얻음
       - 이때 prior distribution은 $p(z'|y;\theta_{pri})=\mathcal{N}(z';\mu(y;\theta_{pri}), \sigma(y;\theta_{pri}))$
     • Duration prediction, learnable upsampling layer, 평균/분산 linear layer를 TTS 모델과 함께 fully-differentiable way로 최적화하여 duration prediction의 training-inference mismatch를 줄일 수 있음
       - 특히 Glow-TTS, VITS 등에서 사용된 hard expansion 대신 soft, flexible 하게 duration을 제공할 수 있으므로 inaccurate duration prediction의 side-effect를 완화 가능

- Bidirectional Prior/Posterior

• NaturalSpeech는 prior $p(z'|y;\theta_{pri})$의 capacity를 enhance 하고 posterior encoder $\phi$에 대해 posterior $p(z'|y;\theta_{pri})$의 complexity를 줄이기 위해 bidirectional prior/posterior module을 도입함
  1. 이때 invertibility의 property를 활용할 수 있는 Flow-based model을 bidirectional prior/posterior module $\theta_{bpp}$로 채택함
  2. Reduce Posterior with Backward Mapping $f^{-1}$
     • Bidirectional prior/posterior module은 backward mapping $f^{-1}(z;\theta_{bpp})$을 통해 $q(z|x;\phi)$에서 $q(z'|x;\phi,\theta_{bpp})$로 posterior complexity를 줄일 수 있음
       - 즉, $z\sim q(z|x;\phi)$이면 $z'=f^{-1}(z;\theta_{bpp})\sim q(z'|x;\phi,\theta_{bpp})$
     • 이때 objective는 KL-divergence loss를 사용하여 simplifed posterior $q(z'|x;\phi,\theta_{bpp})$를 prior $p(z'|y;\theta_{pri})$에 match 하는 것:
       (Eq. 5) $\mathcal{L}_{bwd}(\phi,\theta_{bpp},\theta_{pri})=KL[q(z'| x;\phi,\theta_{bpp})|| p(z'|y;\theta_{pri})]$
       $\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=\int q(z'|x;\phi,\theta_{bpp})\cdot \log \frac{q(z'|x;\phi,\theta_{bpp})}{p(z'|y;\theta_{pri})}dz'$
       $\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=\int q(z|x;\phi)| \det \frac{\partial f^{-1}(z;\theta_{bpp})}{\partial z}|^{-1} \cdot \log \frac{q(z|x;\phi)|\det \frac{\partial f^{-1}(z;\theta_{bpp})}{\partial z} |^{-1}}{p(f^{-1}(z;\theta_{bpp}|y;\theta_{pri}))}\cdot | \det\frac{\partial f^{-1}(z;\theta_{bpp})}{\partial z}|dz$
       $\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=\int q(z|x;\phi)\cdot \log \frac{q(z|x;\phi)}{p(f^{-1}(z;\theta_{bpp}|y;\theta_{pri}))| \det \frac{\partial f^{-1}(z;\theta_{bpp})}{\partial z}|}dz$
       $\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=\mathbb{E}_{z\sim q(z|x;\phi)}\log q(z|x;\phi)-\log \left(p(f^{-1}(z;\theta_{bpp})|y;\theta_{pri})| \det \frac{\partial f^{-1}(z;\theta_{bpp})}{\partial z} |\right)$
       - (Eq. 5)에서 두 번째 줄의 식은 variable change $dz'=| \det \frac{\partial f^{-1}(z;\theta_{bpp})}{\partial z}|dz$로 얻어짐
       - Inverse function theorem에 따라 $q(z'|x;\phi,\theta_{bpp})=q(z|x;\phi)| \det\frac{\partial f(z';\theta_{bpp})}{\partial z'} |=q(z|x;\phi)| \det\frac{\partial f^{-1}(z;\theta_{bpp})}{\partial z}|^{-1}$
  3. Enhance Prior with Forward Mapping $f$
     • Bidirectional prior/posterior module은 forward mapping $f(z';\theta_{bpp})$를 통해 prior의 capacity를 $p(z'|y;\theta_{pri})$에서 $p(z|y;\theta_{pri},\theta_{bpp})$로 enhance 할 수 있음
       - 즉, $z'\sim p(z'|y;\theta_{pri})$의 경우, $z=f(z';\theta_{bpp})\sim p(z|y;\theta_{pri},\theta_{bpp})$
     • 이때 objective는 KL-divergence loss를 기반으로 enhanced prior $p(z|y;\theta_{pri},\theta_{bpp})$를 posterior $q(z|x;\phi)$와 match 하는 것:
       (Eq. 6) $\mathcal{L}_{fwd}(\phi,\theta_{bpp},\theta_{pri})=\text{KL}[p(z|y;\theta_{pri},\theta_{bpp})|| q(z|x;\phi)]$
       $\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,= \int p(z|y;\theta_{pri},\theta_{bpp})\cdot \log \frac{p(z|y;\theta_{pri},\theta_{bpp})}{q(z|x;\phi)}dz$
       $\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=\int p(z'|y;\theta_{pri})|\det \frac{\partial f(z';\theta_{bpp})}{\partial z'} |^{-1}\cdot \log \frac{p(z'|y;\theta_{pri}| \det\frac{\partial f(z';\theta_{bpp})}{\partial z'} |^{-1})}{q(f(z';\theta_{bpp})|x;\phi)} \cdot | \det \frac{\partial f(z';\theta_{bpp})}{\partial z'}|dz'$
       $\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=\mathbb{E}_{z'\sim p(z'|y;\theta_{pri})}\log p(z'|y;\theta_{pri})-\log \left( q(f(z';\theta_{bpp})|x;\phi)|\det \frac{\partial f(z';\theta_{bpp})}{\partial z'} |\right)$
       - (Eq. 6)의 두 번째 줄의 식은 variable change $dz=|\det \frac{\partial f(z';\theta_{bpp})}{\partial z'}|dz'$로 얻어짐
       - (Eq. 5)와 마찬가지로 inverse function theorem에 따라 $p(z|y;\theta_{pri},\theta_{bpp})=p(z'|y;\theta_{pri})| \det \frac{\partial f^{-1}(z;\theta_{bpp})}{\partial z} |=p(z'|y;\theta_{pri})| \det \frac{\partial f(z';\theta_{bpp})}{\partial z'}|^{-1}$
     • 해당 forward/backward loss function을 사용하여 flow-based model을 training 하면, training-inference mismatch를 줄일 수 있음 
  4. Alternative Formulation of Forward/Backward Mapping
     • 추가적으로 두 distribution을 match 하기 위해 KL loss를 직접 사용하는 bidirectional prior/posteriror formulation을 구성할 수 있음
     • 먼저 backward loss의 경우, posterior $q(z|x;\phi)$를 prior $p(z|y;\theta_{pri})$에 directly match 함:
       (Eq. 7) $\mathcal{L}_{bwd}(\phi,\theta_{bpp},\theta_{pri})=\text{KL}[q(z|x;\phi)|| p(z|y;\theta_{pri})]$
       $\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=\mathbb{E}_{z\sim q(z|x;\phi)}\left(\log q(z|x;\phi)-\log p(z|y;\theta_{pri})\right)$
       $\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=\mathbb{E}_{z\sim q(z|x;\phi)}\left(\log q(z|x;\phi)-\log p(f^{-1}(z;\theta_{bpp})|y;\theta_{pri})\right)| \det\frac{\partial f^{-1}(z;\theta_{bpp})}{\partial z} |$
       - 여기서 variable change rule에 따라, $f^{-1}(z;\theta_{bpp})=z'$이고, $p(z|y;\theta_{pri})=p(f^{-1}(z;\theta_{bpp}| y;\theta_{pri})|\det \frac{\partial f^{-1}(z;\theta_{bpp})}{\partial z}|)$
     • Forward loss의 경우, prior $p(z'|y;\theta_{pri})$를 posterior $q(z'|x;\phi)$에 directly match 함:
       (Eq. 8) $\mathcal{L}_{fwd}(\phi,\theta_{bpp},\theta_{pri})=\text{KL}[p(z'|y;\theta_{pri})|| q(z'|x;\phi)]$
       $\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=\mathbb{E}_{z'\sim p(z'|y;\theta_{pri})}\left( \log p(z'|y;\theta_{pri})-\log q(z'|x;\phi)\right)$
       $\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=\mathbb{E}_{z'\sim p(z'|y;\theta_{pri})}\left(\log p(z'|y;\theta_{pri})-\log q(f(z';\theta_{bpp})|x;\phi)\right)| \det \frac{\partial f(z';\theta_{bpp})}{\partial z'}|$
       - 여기서 variable change rule에 따라, $f(z';\theta_{bpp})=z$이고, $q(z'|x;\phi)=q(f(z';\theta_{bpp}|x;\phi)| \det \frac{\partial f(z';\theta_{bpp})}{\partial z'}| )$

- VAE with Memory

• VAE의 posterior $q(z|x;\phi)$는 speech waveform을 reconstruct 하는 데 사용되므로 phoneme sequence의 prior보다 복잡함
  • 따라서 prior prediction의 부담을 완화하기 위해 memory-based VAE를 통해 posterior를 단순화함
  • 즉, wavefrom reconstruction을 위해 $z\sim q(z|x;\phi)$를 직접 사용하는 대신 $z$를 query로 사용하여 memory bank에 attend 하고, reconstruction을 위한 attention result를 사용함
    - 이를 통해 posterior $z$는 memory bank의 attention weight를 결정하는데만 사용됨
  • 결과적으로 memory-based VAE를 통한 waveform reconstruction loss는:
    (Eq. 9) $\mathcal{L}_{rec}(\phi,\theta_{dec})=-\mathbb{E}_{z\sim q(z|x;\phi)}[\log p(x|\mathrm{Attention}(z,M,M);\theta_{dec})],$
    $\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\mathrm{Attention}(Q,K,V)=\left[ \mathrm{softmax}\left( \frac{QW_{Q}(KW_{K})^{T}}{\sqrt{h}} \right)VW_{V}\right]W_{O}$
    - $\theta_{dec}$ : waveform decoder (original waveform decoder의 parameter 뿐만 아니라 memory bank $M$, attention parameter $W_{Q}, W_{K}, W_{V}, W_{O}$도 포함)
    - 이때 $M\in \mathbb{R}^{L\times h}, W_{*} \in \mathbb{R}^{h\times L}$이고, $L$ : memory bank size, $h$ : hidden dimension

Gradient Flow

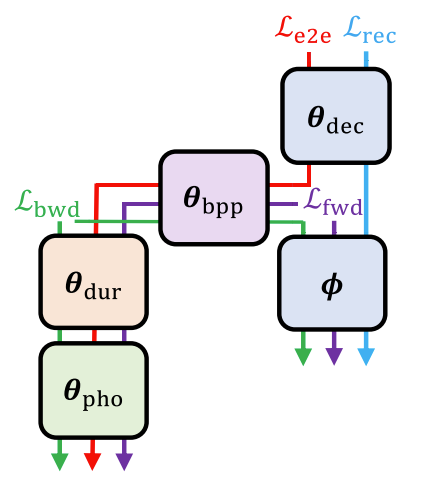
- Training and Inference Pipeline

• Total Training Loss
  • Waveform reconstruction loss와 bidirectional prior/posterior loss 외에 fully end-to-end optimization 추가하여 음성 품질을 향상함 
    • 이때 loss function은:
      (Eq. 10) $\mathcal{L}_{e2e}(\theta_{pri},\theta_{bpp},\theta_{dec})=-\mathbb{E}_{z'\sim p(z'|y;\theta_{pri})}[\log p(x|\mathrm{Attention}(f(z';\theta_{bpp}),M,M);\theta_{dec})]$
    • 그러면 (Eq. 5), (Eq. 6), (Eq. 9), (Eq. 10)에 기반하여 얻어지는 total loss는:
      (Eq. 11) $\mathcal{L}=\mathcal{L}_{bwd}(\phi,\theta_{pri},\theta_{bpp})+\mathcal{L}_{fwd}(\phi, \theta_{pri},\theta_{bpp})+\mathcal{L}_{rec}(\phi,\theta_{dec})+\mathcal{L}_{e2e}(\theta_{pri},\theta_{bpp},\theta_{dec})$
      - $\theta_{pri}=[\theta_{pho},\theta_{dur}]$
  • 결과적으로 NaturalSpeech는 위 그림과 같이 training 시에 여러 개의 gradient flow를 가짐 
    1. $\mathcal{L}_{rec}\rightarrow \theta_{dec}\rightarrow \phi$
    2. $\mathcal{L}_{bwd}\rightarrow \theta_{dur}\rightarrow \theta_{pho}$
    3. $\mathcal{L}_{bwd}\rightarrow \theta_{bpp}\rightarrow \phi$
    4. $\mathcal{L}_{fwd}\rightarrow \theta_{bpp}\rightarrow \theta_{dur}\rightarrow \theta_{pho}$
    5. $\mathcal{L}_{fwd}\rightarrow \phi$
    6. $\mathcal{L}_{e2e}\rightarrow \theta_{dec}\rightarrow \theta_{bpp}\rightarrow \theta_{dur}\rightarrow \theta_{pho}$
  • Trainining 이후 posterior encoder $\phi$를 discard 하고, 추론 시에는 $\theta_{pho}, \theta_{bpp}, \theta_{dur}, \theta_{dec}$만 사용함
    - 전체 training/inference 과정은 아래 [Algorithm 1]을 따름
  • (Eq. 11)의 loss function과 관련하여:
    1. Frame-level prior distribution $p(z'|y;\theta_{pri})$는 durator의 inaccurate prediction으로 인해 ground-truth와 well-align 될 수 없음
       - 따라서 논문은 $\mathcal{L}_{bwd},\mathcal{L}_{fwd}$에 대한 KL loss의 soft dynamic time warping (DTW)를 활용함
    2. Simplicity를 위해 $\mathcal{L}_{rec}, \mathcal{L}_{e2e}$의 waveform loss를 negative log-likelihood로 나타냄
       - 여기서 $\mathcal{L}_{rec}$는 GAN loss, feature matching loss, mel-spectrogram loss로 구성되고 $\mathcal{L}_{e2e}$는 GAN loss로만 구성됨
       - 특히 GAN loss는 mismatched length에서도 잘 동작하므로 $\mathcal{L}_{e2e}$에는 Soft-DTW가 적용되지 않음
• Soft Dynamic Time Warping in KL Loss
  • 일반적으로 frame-level prior distribution $p(z'|y;\theta_{pri})$는 ground-truth speech frame과 length가 다르기 때문에 standard KL loss를 적용할 수 없음
  • 따라서 NaturalSpeech에서는 해당 mismatch를 회피하기 위해 $\mathcal{L}_{bwd}, \mathcal{L}_{fwd}$에 대한 KL loss의 Soft-DTW를 활용함 
    1. 먼저 $\mathcal{L}_{bwd}$에 대한 KL loss의 Soft-DTW는 recursive calculation으로 얻어짐:
       (Eq. 12) $r_{i,j}=\text{min}^{\gamma}\left\{\begin{matrix}
       r_{i-1,j}+\text{KL}[q(z'_{i-1}|x;\phi,\theta_{bpp})|| p(z'_{j}|y;\theta_{pri})]+\text{warp} \\
       r_{i,j-1}+\text{KL}[q(z'_{i}|x;\phi, \theta_{bpp})|| p(z'_{j-1}|y;\theta_{pri})]+\text{warp} \\
       r_{i-1,j-1}+\text{KL}[q(z'_{i-1}|x;\phi,\theta_{bpp})|| p(z'_{j-1}|y;\theta_{pri})]
       \end{matrix}\right.$
       - $r_{i,j}$ : frame $1$에서 frame $i$까지 simplify 된 posterior $q(z'|x;\phi, \theta_{bpp})$와 frame $1$에서 $j$까지의 prior $p(z'|y;\theta_{pri})$ 간의 KL divergence loss
       - 이때 $\text{KL}[q(z'_{*}|x;\phi,\theta_{bpp})||p(z'_{*}|y;\theta_{pri})]$는 (Eq. 5)로 정의됨
       - $\text{min}^{\gamma}$ : soft-min operator로써, $\text{min}^{\gamma}(a_{1},...,a_{n})=-\gamma \log \sum_{i}e^{-\frac{a_{i}}{\gamma}}, \,\, \gamma=0.01$로 정의됨
       - $\text{warp} = 0.07$ : diagonal path를 선택하지 않은 경우에 대한 warp penalty
       - $q(z'_{i}|x;\phi,\theta_{bpp})$ : simplified posterior의 $i$-th frame, $p(z'_{j}|y;\theta_{pri})$ : prior의 $j$-th frame 
    2. $\mathcal{L}_{fwd}$에 대한 KL loss의 Soft-DTW는:
       (Eq. 13) $r_{i,j}=\text{min}^{\gamma}\left\{\begin{matrix}
       r_{i-1,j}+\text{KL}[p(z_{i-1}|y;\theta_{pri},\theta_{bpp})|| q(z_{j}|x;\phi)]+\text{warp} \\
       r_{i,j-1}+\text{KL}[p(z_{i}|y;\theta_{pri},\theta_{bpp})|| q(z_{j-1}|x;\phi)]+\text{warp} \\
       r_{i-1,j-1}+\text{KL}[p(z_{i-1}|y;\theta_{pri},\theta_{bpp})|| q(z_{j-1}|x;\phi)]
       \end{matrix}\right.$
       - $r_{i,j}$ : frame $1$에서 frame $i$까지의 enhanced prior $p(z|y;\theta_{pri},\theta_{bpp})$와 frame $1$에서 $j$까지의 posterior $q(z|x;\phi)$ 간의 KL divergence loss
       - $\text{KL}[p(z_{*}|y;\theta_{pri}, \theta_{bpp}||q(z_{*}|x;\phi)]$는 (Eq. 6)으로 정의됨
       - $p(z_{i}|y;\theta_{pri},\theta_{bpp})$ : enhanced prior의 $i$-th frame, $q(z_{j}|x;\phi)$ : posterior의 $j$-th frame
• Waveform Decoder Loss
  • (Eq. 9), (Eq. 10)의 waveform reconstruction과 prediction에서 negative log-likelihood 대신, GAN loss, feature matching loss, mel-spectrogram loss를 사용함 (이때 HiFi-GAN의 구성을 따름)
  • GAN Loss
    - Least-Square GAN을 따라 generator는 $\mathcal{L}_{G}$로, discriminator는 $\mathcal{L}_{D}$로 training 됨:
    (Eq. 14) $\mathcal{L}_{G}=\mathbb{E}_{z}[1-D(G(z))^{2}], \,\, \mathcal{L}_{D}=\mathbb{E}_{(x,z)}[1-D(x)^{2} +D(G(z))^{2}]$
    - $x$ : ground-truth waveform, $z$ : waveform decoder의 input
  • Feature Matching Loss
    - Feature matching loss는 discriminator 각 layer의 intermediate feature에서 ground-truth sample과 fake sample 간의 $L1$ distance로 계산됨:
    (Eq. 15) $\mathbb{E}_{(x,z)}\left[\sum_{l}\frac{1}{N_{l}}|| D^{l}(x)-D^{l}(G(z)) ||_{1}\right]$
    - $l$ : discriminator의 layer index
    - $D^{l}(\cdot), N_{l}$ : 각각 discriminator의 $l$-th layer의 feature와 feature 수
  • Mel-Spectrogram Loss
    - Ground-truth waveform과 생성된 waveform 간의 $L1$ distance:
    (Eq. 16) $\mathbb{E}_{(x,z)} =|| S(x)-S(G(z))||_{1}$
    - $S(\cdot)$ : waveform을 mel-spectrogram으로 변환하는 function

Training, Inference Algorithm

- Advantages of NaturalSpeech

• NaturalSpeech가 human-level quality를 달성할 수 있는 이유를 요약하면 다음과 같음
  1. Reduce Training-Inference Mismatch
     • NaturalSpeech는 text에서 직접 waveform을 생성하고 differentiable durator를 통해 fully end-to-end optimization을 보장함
       - 이를 통해 기존 cacaded TTS의 training-inference mismatch 문제를 해결
     • 특히 VAE와 Flow는 본질적인 training-inference mismatch를 가지고 있지만, (Eq. 5), (Eq. 6)의 backward/forward loss와 (Eq. 10)의 end-to-end loss를 통해 완화 가능
  2. Alleviate One-to-Many Mapping Problem
     
     • NaturalSpeech에서 VAE의 posterior encoder $\phi$는 posterior distribution $q(z|x;\phi)$에서 필요한 모든 variance information을 추출하는 reference encoder로 동작함
       - 여기서 $F0$는 VAE의 posterior encoder와 memory bank에서 implicitly learnt 되므로 explicit 하게 예측하지 않음
     • 추가적으로 bidirectional prior/posterior module에서 memory VAE 및 backward mapping을 통해 prior를 향상하고 posterior를 단순화함 
       - 이를 통해 one-to-many mapping 문제를 크게 완화함
  3. Increase Representation Capacity
     • Large-scale phoneme pre-training을 통해 phoneme sequence에서 better representation을 추출하고, VAE와 같은 generative model을 통해 speech data dsitribution을 효과적으로 capture 함
     • 이를 통해 NaturalSpeech의 representation capacity를 향상함

4. Experiments

- Settings

• Dataset : LJSpeech, VCTK
• Comparisons : FastSpeech2, Glow-TTS, Grad-TTS, VITS

- Results

• Comparison with Human Recordings
  • MOS, CMOS 측면에서 NaturalSpeech는 human recording과 큰 차이를 보이지 않음

Human Recording에 대한 MOS, CMOS 비교 (LJSpeech)

• VCTK dataset에서도 마찬가지의 결과를 달성함

Human Recording에 대한 CMOS 비교 (VCTK)

• Comparison with Previous TTS Systems
  • 기존 TTS 모델과 비교하여 NaturalSpeech는 가장 우수한 성능을 보임

모델 성능 비교

• Ablation Study
  • Ablation study 측면에서 각 component를 제거하는 경우 NaturalSpeech의 성능 저하가 발생함

Ablation Study 결과

• 추가적으로 latency 측면에서도 NaturalSpeech는 FastSpeech2 수준의 빠른 추론 속도를 달성함

추론 속도 비교