[Paper 리뷰] EmoMix: Emotion Mixing via Diffusion Models for Emotional Speech Synthesis

EmoMix: Emotion Mixing via Diffusion Models for Emotional Speech Synthesis

---

• Emotional Text-to-Speech는 여전히 intensity control 측면에서 한계가 있음
• EmoMix
  • Emotion embedding을 추출하기 위해 pre-trained Speech Emotion Recognition model을 활용
  • Run-time 시 diffusion model을 기반으로 mixed emotion synthesis를 수행
• 논문 (INTERSPEECH 2023) : Paper Link

---

1. Introduction

• GenerSpeech와 같은 emotional Text-to-Speech (TTS) model은 reference-based style transfer를 주로 활용함
  • 이때 Speech Emotion Recognition (SER), Automatic Speech Recognition (ASR) model의 특정 layer에서 추출된 intermediate embedding을 활용하면 expressiveness를 향상할 수 있음
    
  • 한편으로 internal emotion representation을 manipulate 하기 위해 scaling, interpolation, distance-based quantization 등을 활용할 수 있지만 여전히 controllability 측면에서 한계가 있음
    1. 특히 대부분 limited emotion type에 대해서만 synthesis를 수행하므로 서로 다른 emotion 간의 interaction을 효과적으로 반영하지 못함
    2. 이를 해결하기 위해 EmoDiff는 Denoising Diffusion Probabilistic Model (DDPM)을 기반으로 classifier guidance를 도입함
       - BUT, 해당 classifier는 high-dimensional, unseen primary emotion conditioning에 inefficient 함

-> 그래서 효과적인 intensity control과 mixed emotion synthesis를 지원하는 EmoMix를 제안

 

• EmoMix
  • Pre-trained SER model을 통해 추출된 emotion embedding을 diffusion model의 extra condition으로 사용
  • Intensity control, mixed emotion을 지원하기 위해 run-time 내에서 하나의 sampling process로 서로 다른 emotional condition을 combine

< Overall of EmoMix >

• Diffusion model과 pre-trained SER model을 활용한 emotional TTS model
• 결과적으로 기존보다 뛰어난 controllability와 합성 품질을 달성

2. Method

- Preliminary on Score-based Diffusion Model

• EmoMix는 GradTTS를 기반으로 Stochastic Differential Equation (SDE)를 TTS에 적용함
  • 먼저 data distribution $X_{0}$를 standard Normal distribution $X_{T}$로 convert 하는 diffusion process는:
    (Eq. 1) $dX_{t}=-\frac{1}{2}X_{t}\beta_{t}dt+\sqrt{\beta_{t}}d W_{t},t\in[0,T]$
    - $\beta_{t}$ : pre-defined noise schedule, $W_{t}$ : Wiener process
  • SDE는 다음과 reverse process를 formulate 함:
    (Eq. 2) $dX_{t}=\left(-\frac{1}{2}X_{t}-\nabla_{X_{t}}\log p_{t}(X_{t})\right)\beta_{t}dt+\sqrt{\beta_{t}}dt +\sqrt{\beta_{t}}d\tilde{W}_{t}$
  • Sampling 시에는 standard Gaussian noise $X_{T}$에서 data $X_{0}$를 생성하기 위해 다음과 같은 reverse SDE의 discretized version을 사용함:
    (Eq. 3) $X_{t-\frac{1}{N}}=X_{t}+\frac{\beta_{t}}{N}\left(\frac{1}{2}X_{t}+\nabla_{X_{t}} \log p_{t}(X_{t})\right)+\sqrt{\frac{\beta_{t}}{N}}z_{t}$
    - $N$ : step 수, $z_{t}$ : standard Gaussian noise
    - GradTTS에서는 $T=1$, one step size를 $\frac{1}{N}$, $t\in\{\frac{1}{N},\frac{2}{N},...,1\}$로 설정함
  • Data $X_{0},X_{t}$는 (Eq. 1)에서 derive 된 distribution에서 sampling 되어, score $\nabla_{X_{t}}\log p_{t}(X_{t})$를 estimate 함:
    (Eq. 4) $X_{t}|X_{0}\sim\mathcal{N}\left(\rho(X_{0},t),\lambda(t)\right)$
    - $\rho(X_{0},t)=e^{-\frac{1}{2}\int_{0}^{t}\beta_{s}ds}X_{0}, \lambda(t)=I-e^{-\int_{0}^{t}\beta_{s}ds}$
  • (Eq. 3)은 score $\nabla_{X_{t}}\log p_{t}(X_{t}|X_{0})=-\lambda(t)^{-1}\epsilon_{t}$를 derive 하고, 해당 score를 estimate 하기 위해서는 $\forall t\in[0,T]$에 대해 $\epsilon_{\theta}(X_{t},t,\mu,s,e)$를 training 해야 함
    - $\epsilon_{t}$ : $X_{0}$가 주어졌을 때 $X_{t}$를 sampling 하기 위한 standard Gaussian noise
    - $\mu$ : speaker $s$, emotion $e$에 condition 된 phoneme-dependent Gaussian mean
  • 이때 loss는:
    (Eq. 5) $\mathcal{L}_{diff}=\mathbb{E}_{x_{0},t,e,\epsilon_{t}}\left[ \lambda_{t}||\epsilon_{\theta}(x_{t},t,e)+\lambda(t)^{-1}\epsilon_{t}||_{2}^{2}\right]$
    - 논문에서는 emotion에 focus 하므로 $\epsilon_{\theta}(X_{t},t,\mu,s,e)$를 $\epsilon_{\theta}(X_{t},t,e)$로 simplify 함

Overview

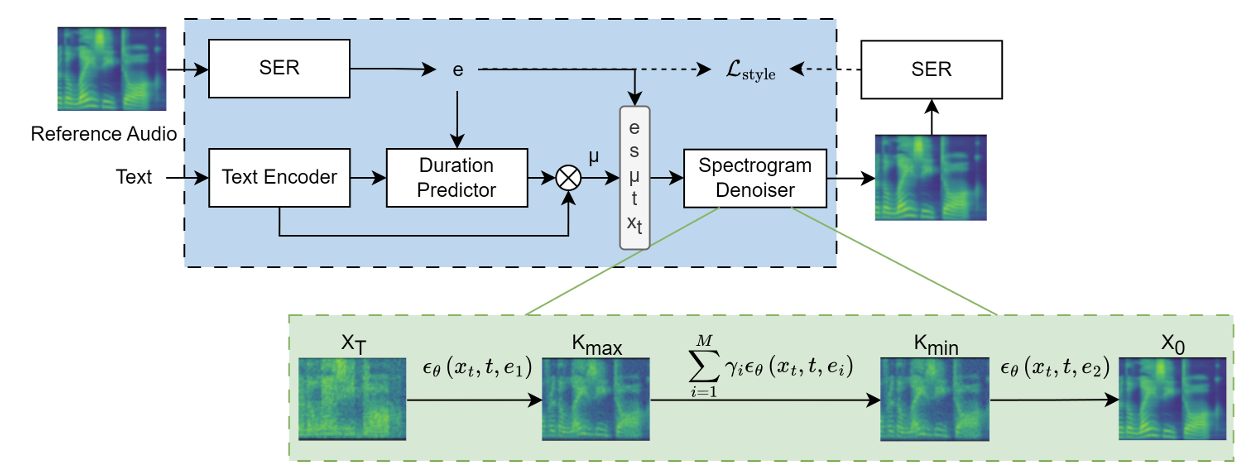
- Emotion Conditioning with SER

• EmoDiff는 classifier의 log-probability에 대한 gradient로 guide 되는 single-speaker emotional TTS를 고려함
  • 한편으로 논문은 continuous emotion embedding $e$를 생성하는 pre-trained SER model을 활용함
    1. 먼저 3D CNN layer는 mel-spectrum과 해당 derivative를 input으로 사용하여 emotional content를 encode 하는 latent representation을 추출함
    2. BLSTM과 attention layer는 utterance-level emotion classification을 위한 emotion embedding $e$를 생성함
       - Speaker conditioning의 경우 GenerSpeech와 같이 Wav2Vec 2.0을 사용하여 speaker acoustic condition $s$를 capture 함
  • EmoMix에서 predicted duration은 emotion, speaker에 따라 condition 되고, hidden representation $\mu$는 input text, emotion embedding $e$, speaker embedding $s$를 반영함
    1. 이후 spectrogram denoiser는 reference audio의 target primary emotion과 speaker를 사용하여 $\mu$를 mel-spectrogram으로 iteratively refine 함
    2. 추가적으로 논문은 또 다른 SER을 사용하여 denoiser와 함께 reference speech와 synthesis speech 간의 emotion style gap을 minimize 함
    3. 이때 style reconstruction loss는:
       (Eq. 6) $ \mathcal{L}_{style}=\sum_{j}\left|\left| G_{j}(\hat{m})-G_{j}(m)\right|\right|_{F}^{2}$
       - $G_{j}(x)$ : SER model의 input $x$에 대한 $j$-th 3D CNN layer feature map의 gram matrix
       - $m,\hat{m}$ : 각각 reference/synthesized mel-spectrogram
  • Style reconstruction loss는 synthesized speech가 reference audio와 비슷하도록 enforce 하고, 결과적으로 얻어지는 final training loss는 다음과 같음:
    (Eq. 7) $\mathcal{L}=\mathcal{L}_{dur}+\mathcal{L}_{diff}+\mathcal{L}_{prior}+\gamma \mathcal{L}_{style}$
    - $\mathcal{L}_{dur}$ : logarithmic duration의 $\ell_{2}$ loss, $\mathcal{L}_{diff}$ : (Eq. 5)의 diffusion loss
    - $\gamma=1e-4$ : hyperparameter, $\mathcal{L}_{prior}$ : Grad-TTS의 prior loss

- Run-Time Emotion Mixing

• EmoMix는 mixed emotion과 다양한 intensity의 single primary emotion에 대한 TTS를 목표로 함
  • 이를 위해 논문은 single primary emotion으로 condition 된 trained DDPM의 reverse process를 extend 하여 mixed emotion을 synthesize 함
  • 특히 추론 시에 $K_{\max}$ sampling step 이후의 condition vector를 replace 하여 base emotion detail을 mixed-in emotion으로 overwrite 함
    1. 먼저 single reference audio의 instability를 avoid 하기 위해 same primary emotion에 대한 audio sample의 emotion embedding을 average 함
    2. 이후 base emotion condition $e_{1}$을 intermediate step $K_{\max}$까지 Gaussian noise로부터 denoising을 수행하여 coarse base emotion prosody를 synthesize 하고,
       - $K_{\min}$ 부터 mixed-in emotion $e_{2}$에 대한 condition으로 denoising을 수행하여 emotion mixture를 얻음
  • 여기서 논문은 $K_{\max}$에서 $K_{\min}$ 까지 주어진 base emotion을 preserve 하고 mixed-in emotion으로 easily overwritten 되는 것을 방지하기 위해, noise combine approach를 도입함
    1. 즉, multiple emotion condition에서 predicted noise를 combine 하여 one sampling process를 통해 multiple emotion style를 synthesize 함
    2. 그러면 multiple noise는 다음과 같이 combine 됨:
       (Eq. 8) $\epsilon_{\theta}(x_{t},t,e_{mix})=\sum_{i=1}^{M}\gamma_{i}\epsilon (x_{t},t,e_{i})$
       - $\gamma_{i}$ : $\sum_{i=1}^{M}\gamma_{i}=1$를 만족하는 각 condition $e_{i}$의 weight로써, emotion degree를 control 하는 역할
       - $M$ : mixed-in emotion category 수
    3. (Eq. 8)에서 sampling process는 다음의 conditional distribution의 joint probability를 increase 하는 것으로 interpret 될 수 있음:
       (Eq. 9) $\sum_{i=1}^{M}\gamma_{i}\epsilon_{\theta}(x_{t},t,e_{i})\propto -\nabla_{x_{t}}\log\prod_{i=1}^{M} p(x_{t}|e_{tar,i})^{\gamma_{i}}$
       - $e_{tar,i}$ : specified target emotion condition
  • 추가적으로 논문은 emotion intensity control을 위해 Neutral condition에서 specified primary emotion을 다양한 $\gamma$로 mixing 하여 Neutral과 target emotion을 smoothly interpolate 함

3. Experiments

- Settings

• Dataset : IEMOCAP
• Comparisons : MixedEmotion, EmoDiff

- Results

• 전체적으로 EmoMix의 성능이 가장 우수함

Model 성능 비교

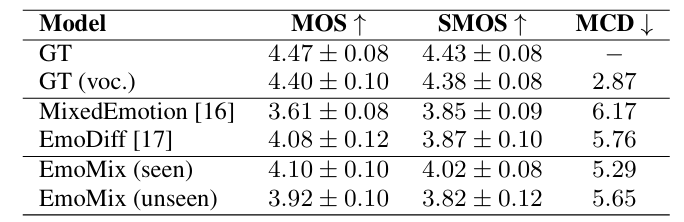
• Ablation Study
  • 각 component를 제거하는 경우 성능 저하가 발생함

Ablation Study

• Evaluation of Mixed Emotion
  • Mixed-in emotion noise를 변경하여 desired mixed emotion을 control 할 수 있음

SER Model의 Classification Probability

• CMOS 측면에서도 EmoMix의 mixing method는 MixedEmotion에 비해 낮은 품질 저하를 보임

Mixed Emotion에 대한 CMOS

• Confusion matrix 측면에서도 EmoMix의 sample은 desired intensity를 accurately reflect 함

Synthesized Mixed Emotion에 대한 Confusion Matrix