[Paper 리뷰] OZSpeech: One-Step Zero-Shot Speech Synthesis with Learned-Prior-Conditioned Flow Matching

OZSpeech: One-Step Zero-Shot Speech Synthesis with Learned-Prior-Conditioned Flow Matching

---

• Waveform, spectrogram과 같은 기존의 speech representation은 speech attribute를 overlooking 하고 high computational cost를 가짐
• OZSpeech
  • One-step sampling과 learned prior를 condition으로 사용하여 sampling step 수를 reduce
  • Token format의 disentangled, factorized component를 활용하여 speech attributre를 modeling
• 논문 (ACL 2025) : Paper Link

---

1. Introduction

• Zero-shot Text-to-Speech (TTS)는 주어진 text에 대해 unseen speaker의 acoustic characteristic을 따르는 speech를 생성하는 것을 목표로 함
  • 먼저 VALL-E와 같은 autoregressive approach의 경우 language modeling을 integrate 하고 disentangled speech unit을 활용하여 zero-shot TTS의 성능을 향상함
    - BUT, autoregressive system은 non-deterministic sampling process에 susceptible 하므로 infiite repetition이 발생할 수 있음
  • 한편으로 VoiceBox, E2-TTS, NaturalSpeech2, NaturalSpeech3와 같은 diffusion-based model 역시 high-quality, natural-sounding audio를 생성할 수 있음
    1. BUT, diffusion-based model은 multi-step sampling process의 computational inefficiency로 인해 real-time application에서 활용하기 어려움
    2. Multi-step sampling 문제를 해결하기 위해 Consistency model이나 Shortcut model 등을 고려할 수 있지만 complex training process가 요구됨

-> 그래서 diffusion-based model의 multi-step sampling 문제를 해결한 zero-shot TTS model인 OZSpeech를 제안

 

• OZSpeech
  • Optimal Transport-Conditional Flow Matching (OT-CFM)을 reformulate 하여 single-step sampling을 지원
  • Initial point와 origin 간의 distance를 minimize 하면서 각 prior에 대해 optimal $t$를 implicitly learning

< Overall of OZSpeech >

• Learned-Prior-Conditioned Flow Matching을 활용한 one-step zero-shot TTS model
• 결과적으로 기존보다 빠른 latency와 우수한 성능을 달성

2. Method

- Problem Statement

• 논문은 주어진 text와 acoustic prompt로부터 condition을 만족하는 speech를 생성하는 것을 목표로 함
  • 기존에는 synthesized speech의 data distribution을 $\mathbf{x}_{1}\sim p_{1}(x)$라고 했을 때, output data distribution을 noise distribution $\mathbf{x}_{0}\sim p_{0}(x)$로부터 construct 함
  • 대신 논문은 feasible intermediate state candidate인 $\mathbf{x}_{pr}\sim p_{prior}(x)$에서 output data distribution을 construct 함
    - 이를 통해 preceding state를 disregarding 하고 sampling step을 줄임
  • 결과적으로 OZSpeech는 다음의 step을 수행함:
    1. Prior Code Generation
       - $\mathbf{x}_{pr}$을 위한 prior code를 생성함
    2. Vector Field Estimation
       - $v_{\theta}$를 approximate 하는 vector field estimator를 활용하여 $\mathbf{x}_{pr}$에서 $\mathbf{x}_{1}$로의 transition을 지원함
    3. Waveform Decomposition via FACodec
       - Neural codec disentangler framework인 FACodec을 활용하여 waveform을 speaker identity, prosody, content, acoustic detail의 distinct component로 decompose 함

- Prior Codes Generation Modeling

• Prior code generation은 hierarchical structure를 따름
  • 즉, 각 code sequence generation은 preceding code sequence에 의존하고 first code sequence의 condition은 phoneme embedding으로 initialize 됨
    1. 이를 위해 논문은 specific decoder layer가 hierarchical structure에서 respective code sequence를 생성하는 cascaded neural network를 도입함
    2. 그러면 Prior Code Generator $\mathbf{f}_{\psi}(\cdot)$은:
       (Eq. 1) $ p(\mathbf{q}_{1:6}|\mathbf{p};\psi)=p(\mathbf{q}_{1}|\mathbf{p};f_{\psi}^{1})\prod_{j=2}^{6} p(\mathbf{q}_{j}|\mathbf{q}_{j-1};f_{\psi}^{j})$
       - $\mathbf{q}_{j}$ : Feed-Forward Transformer (FFT) decoder layer $f_{\psi}^{j}$의 $j$-th code sequence
       - $\mathbf{p}$ : phoneme embedding
  • Prior loss $\mathcal{L}_{prior}$는 (Eq. 1)의 joint probability에 대한 negative logarithm을 minimize 하여 content code sequence가 phoneme을 condition으로 effectively learned 되도록 함
    - 그 외의 prosody, acoustic detail은 mean representation으로 converge 하게 함
  • 결과적으로 Prior Code Generator는 semantically meaningful code를 생성하고, $\mathbf{x}_{pr},\mathbf{x}_{1}$ 간의 distance를 reduce 함
    - 이를 통해 Vector Field Estimator $\mathbf{v}_{\theta}(\cdot,\cdot)$이 pure noise가 아닌 mean distribution에서 vector를 approximate 하도록 함
  • 추가적으로 input phoneme을 output code sequence와 align 하기 위해, 논문은 FastSpeech의 Duration Predictor를 도입함
    1. 이때 Duration Predictor는 각 input phoneme에 대한 duration (acoustic token 수)를 estimate 함
    2. Duration Predictor training 시에는 predicted/ground-truth duration 간의 Mean Squared Error에 해당하는 $\mathcal{L}_{dur}$를 loss로 사용함 

Overview

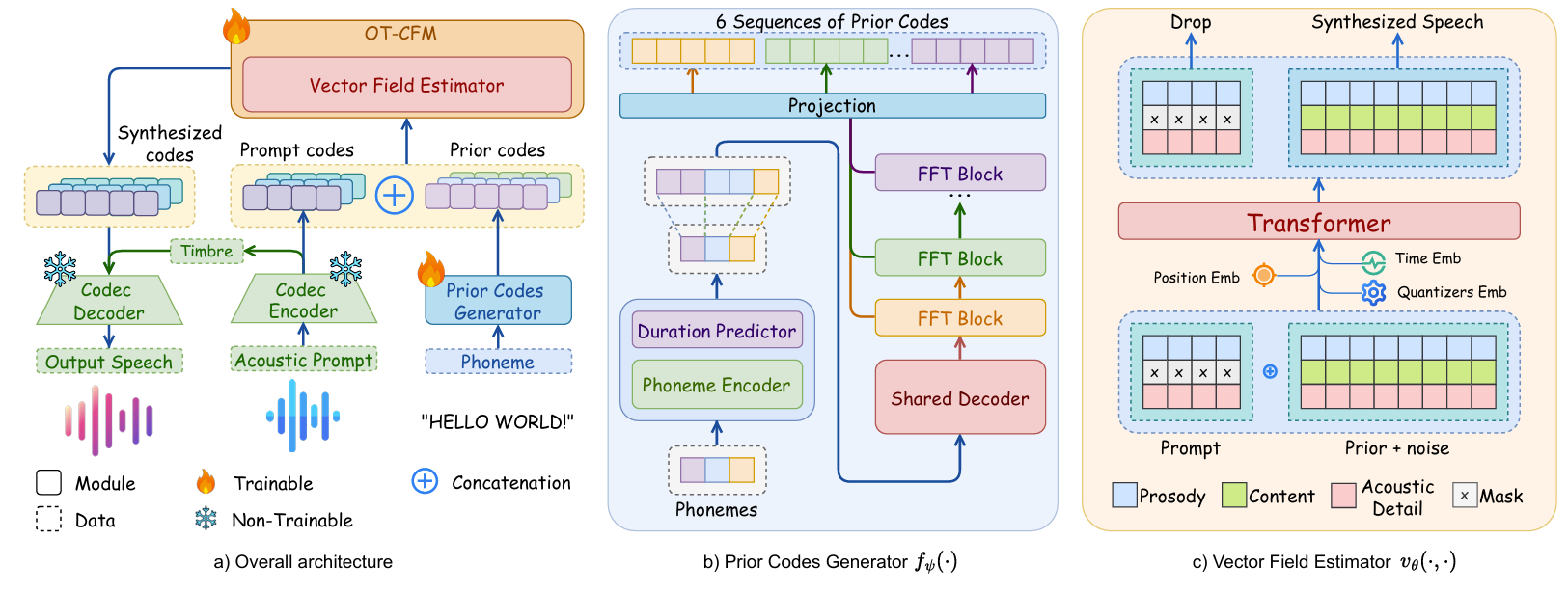
- One-Step Optimal Transport Flow Matching for Zero-Shot TTS

• One-Step Optimal Transport Flow Matching Formulation
  • 논문은 OT-CFM을 기반으로 non-Gaussian distribution과 data distribution pair의 velocity를 regress 하는 vector field를 construct 하는 것을 목표로 함
  • 이때 non-Gaussian initial distribution과 target distribution 간의 discrepancy를 explicit 하게 고려하도록 flow matching loss equation을 reformulate 함
    1. 먼저 $\mathbf{x}_{t}$를 puerly noisy initial point $\mathbf{x}_{0}\sim\mathcal{N}(0,I)$에서 start 하여 data point $\mathbf{x}_{1}\sim\mathcal{D}$로 progress 하는 linear probability path라고 하자
       - 즉, interpolation parameter $t\sim \mathcal{U}(0,1)$에 대해 $\mathbf{x}_{t}=t\mathbf{x}_{1}+(1-t)\mathbf{x}_{0}$와 같음
    2. 여기서 initial point $\mathbf{x}_{0}$는 $\mathbf{x}_{0}=\frac{t\mathbf{x}_{1}-\mathbf{x}_{t}}{1-t}$와 같이 derive 됨
    3. 그러면 OT-CFM objective는 다음과 같이 reformulate 됨:
       (Eq. 2) $ \mathcal{L}_{CFM}(\theta)=\mathbb{E}_{t,\mathbf{x}_{0},\mathbf{x}_{1}}\left|\left| \mathbf{v}_{\theta}(\mathbf{x}_{t},t)=\frac{\mathbf{x}_{t}-\mathbf{x}_{1}}{1-t}\right|\right|^{2}$
  • 논문은 $\mathbf{x}_{t}$가 $\mathbf{f}_{\psi}(\cdot)$에 의해 estimate 될 수 있다고 가정함
    1. 해당 가정하에서, $\mathbf{x}_{t}$는 learnable state $\mathbf{x}_{pr}$로 취급됨
       - 이때 $t$는 unknown interpolation parameter로써 prior-dependent time variable $\tau$로 represent 됨
    2. 결과적으로 (Eq. 2)는 다음과 같이 reformulate 됨:
       (Eq. 3) $\mathcal{L}_{CFM}(\theta)=\mathbb{E}_{\mathbf{x}_{pr},\mathbf{x}_{1}}\left|\left| \mathbf{v}_{\theta}(\mathbf{x}_{pr},\tau)- \frac{\mathbf{x}_{1}-\mathbf{x}_{pr}}{1-\tau}\right|\right|^{2}$
  • 해당 paradigm은 initial prior $\mathbf{x}_{0}$와 data $\mathbf{x}_{1}$ 간의 velocity를 regress 하는 original OT-CFM과 유사하다고 볼 수 있음
    - BUT, 기존 방식과 달리 training 중에 $\mathbf{x}_{0}$ distribution에 access 하지 않고, $\mathbf{x}_{0}$가 Normal distribution을 따르도록 enforce 하지 않음
  • 특히 prior distribution $\mathbf{x}_{pr}$이 target distribution $\mathbf{x}_{1}$에 approach 함에 따라 sampling step과 각 step의 magnitude가 줄어듦
    - 이를 통해 sampling process는 single-step 만으로도 efficiently perfom 될 수 있음
• Vector Field Estimator Modeling
  • $\mathbf{v}_{\theta}(\cdot,\cdot)$을 modeling 하기 위해 prior, target, estimated target distribution의 latent reprsentation을 $\mathbf{x}_{pr}, \mathbf{x}_{1},\tilde{\mathbf{x}}_{1}$이라고 하자
    - $\mathbf{x}_{pr},\mathbf{x}_{1},\tilde{\mathbf{x}}_{1}\in\mathbb{R}^{6\times N\times D}$
    - $N$ : sequence length, $D$ : feature dimension
  • 이때 논문은 acoustic prompt에 대해 $\mathbf{x}_{pr}$을 condition 하여 $\mathbf{v}_{\theta}(\cdot, \cdot)$이 content 이외의 speech attribute를 transfer 하도록 guide 함
    1. 여기서 prosody, acoustic detail code만 prompt로 사용되고, content code는 undesired content transfer를 방지하기 위해 masking 됨
    2. $\mathbf{v}_{\theta}(\cdot, \cdot)$에 대한 input은 concatenated representation으로 formulate 됨:
       (Eq. 4) $\mathbf{z}_{pr}=\text{Concat}\left(\mathbf{y}_{mask}, \mathbf{x}_{pr}+\epsilon\right),\,\, \epsilon\sim \mathcal{N}(0,I)$
       - $\mathbf{z}_{pr}\in\mathbb{R}^{6\times L\times D}$, $L=M+N$ : concatenated input의 total sequence length
       - $\mathbf{y}_{mask}$ : acoustic prompt의 content-masking representation
       - $\epsilon$ : random Gaussian noise
• Folding Mechanism and Quantizer Encoding
  • OZSpeech의 data representation은 quantizer embedding의 6-sequence로 구성되므로 Transformer를 통한 direct sequence modeling이 어려움
    1. VALL-E, NaturalSpeech3 등과 같은 기존의 audio discretization TTS model에서 각 quantizer sequence는 independently modeling 됨
    2. BUT, 해당 방식은 sequential processing으로 인해 high computational cost를 가짐
  • 따라서 논문은 hidden dimension에서 6-quantizer를 folding 하여 simultanesouly modeling 함
    1. 먼저 $\mathcal{F}(\cdot)$을 2가지의 transformation $\mathcal{G}:\mathbb{R}^{6\times L\times D}\rightarrow \mathbb{R}^{L\times 6D}$, $\mathcal{H}:\mathbb{R}^{L\times 6D}\rightarrow \mathbb{R}^{L\times D'}$으로 정의되는 folding function이라고 하자
    2. 그러면 $\mathcal{F}(\cdot)$은 input tensor를 permutes, reshape 하고 hidden space에서 component quantizer를 sequentially align 하고 tensor dimensionality를 adjust 함
  • 추가적으로 논문은 hidden space에서 specific quantizer를 identify 하기 위해 $\mathcal{F}(\cdot)$과 함께 operate 하는 quantizer encoding mechanism을 도입함
    1. 이때 quantizer encoding은:
       (Eq. 5) $\mathcal{Q}(x)=x+\text{Dup}(\omega,L),\,\,x\in\mathbb{R}^{6\times L\times D}$
    2. 여기서 quantizer encoding function $\mathcal{Q}(\cdot)$은 embedding $\text{Dup}(\omega, L)$과 함께 input tensor $\mathbb{R}^{6\times L\times D}$를 integrate 함
       - $\omega\in\mathbb{R}^{6\times 1\times D}$ : quantizer의 latent representation에 대한 identifier
       - $\text{Dup}(\cdot,\cdot)$ : sequence length $L$을 따라 identifier를 duplicate 하는 역할
    3. 해당 $\mathcal{Q}(\cdot)$을 통해 model이 quantizer를 confusing 하는 것을 방지할 수 있음
  • 결과적으로 latent representation $\mathbf{x}_{pr}$은 $\breve{\mathbf{z}}_{pr}$로 transform 된 다음, function $\mathbf{v}_{\theta}(\cdot, \cdot)$에 direct input 됨
    - 즉, $\breve{\mathbf{z}}_{pr}=(\mathcal{F}\circ\mathcal{Q})(\mathbf{z}_{pr})$
• Anchor Loss
  • Discrete token에 대한 generative model performance를 optimize 하고 training을 stabilize 하기 위해 anchor loss $\mathcal{L}_{anchor}$를 regularization term으로 사용함
    1. $\mathcal{L}_{anchor}$는 intermediate state $\mathbf{x}_{t}$와 ground-truth $\mathbf{x}_{1}$ 간의 difference를 measure 함
    2. 이를 통해 embedding collapse를 방지하고 state 간 distance를 reduce 하고, efficient sampling을 보장함
       - OZSpeech에서 $\mathcal{L}_{anchor}$는 joint probability (Eq. 6)의 negative log-likelihood를 minimize 함
  • $\mathbf{e}_{\phi}(\cdot)=[e_{1},e_{2},...,e_{V}]\in\mathbb{R}^{V\times D}$를 vocabulary size $V$인 embedding lookup function이라고 하자
    1. Sequence length $L$인 $\mathbf{x}_{1}$의 quantizer element에 해당하는 $\mathcal{A}^{6\times L}=\{\alpha_{i,j}|i=1...6|j=1...L\}$이 주어지면, $\mathcal{A}^{6\times L}$의 embedding은 $ \mathbf{e}_{\phi}(\mathcal{A}^{6\times L})=\{\epsilon_{i,j}|i=1...6;j=1...L\}$로 express 됨
       - $\alpha_{i,j}\in\{1...V\}, \epsilon_{i,j}\in\mathbb{R}^{D}$
    2. 따라서 estimated sequence $\tilde{\mathbf{z}}_{1}$에 condition 된 target distribution $\mathbf{z}_{1}$을 approximate 하는 joint probability는:
       (Eq. 6) $p(\mathbf{z}_{1}|\tilde{\mathbf{z}}_{1};\phi)=\prod_{i=1}^{6}\prod_{j=1}^{L}p(\epsilon_{i,j}| \tilde{\epsilon}_{i,j};\mathbf{e}_{\phi})$
       - $\tilde{\mathbf{z}}_{1}$ : estimated vector $\mathbf{v}_{\theta}(\breve{\mathbf{z}}_{pr},\tau)$, prior state $\mathbf{z}_{pr}$, interpolate parameter $\tau$의 triplet으로부터 deduce 되는 $\mathbf{z}_{1}$의 approximation
  • $\mathcal{F}^{-1}$을 $\mathcal{F}$의 reverse function이라고 하면, $\tilde{\mathbf{z}}_{1}=\mathbf{z}_{pr}+(1-\tau)\mathcal{F}^{-1} \left(\mathbf{v}_{\theta}(\breve{\mathbf{z}}_{pr},\tau)\right)$의 relationship을 가짐
• Total Loss
  • Joint training에서 사용되는 total loss는:
    (Eq. 7) $\mathcal{L}_{total}=\mathcal{L}_{prior}+\mathcal{L}_{dur}+\mathcal{L}_{CFM}+\mathcal{L}_{anchor}$
  • $\mathcal{L}_{prior}, \mathcal{L}_{dur}$는 Prior Code Generator에 대한 training objective로 사용되고, $\mathcal{L}_{CFM}, \mathcal{L}_{anchor}$는 vector field construction과 sampling step distill에 사용됨

3. Experiments

- Settings

• Dataset : LibriTTS
• Comparisons : F5-TTS, VoiceCraft, NaturalSpeech2, VALL-E

- Results

• 전체적으로 OZSpeech의 성능이 가장 우수함

Model 성능 비교

• Latency, model size 측면에서도 OZSpeech가 가장 efficient 함

Model Size, Latency 비교

• Ablation Study
  • Arbitrary Segment strategy가 First Segment strategy 보다 더 나은 성능을 보임

Prompt Setting 비교

• Noise Tolerance
  • OZSpeech는 noisy audio prompt에 대해서도 robust 한 성능을 보임

Noise Tolerance