[Paper 리뷰] EmoDiff: Intensity Controllable Emotional Text-to-Speech with Soft-Label Guidance

EmoDiff: Intensity Controllable Emotional Text-to-Speech with Soft-Label Guidance

---

• 최신 Text-to-Speech 모델들은 고품질 음성을 합성할 수 있지만, emotion에 대한 intensity controllability는 떨어짐
  - Intensity 계산을 위한 external optimization이 필요하기 때문
• EmoDiff
  • Classifier guidance에서 파생된 soft-label guidance를 diffusion 기반 text-to-speech 모델에 적용
  • Specified emotion과 Neutral을 emotion intensity $\alpha, 1-\alpha$로 나타내는 soft-label을 활용
• 논문 (ICASSP 2023) : Paper Link

---

1. Introduction

• Grad-TTS, VITS와 같은 최신 text-to-speech (TTS) 모델들은 좋은 합성 품질을 보이고 있지만, intensity controllable emotional TTS에는 어려움이 있음
  • 일반적으로 Emotional TTS 작업은 categorical emotion label을 가지는 dataset을 활용하여 수행됨
  • 이때 TTS 모델들은 학습 중에 emotion intensity value를 계산하는 것이 필요함
    - 대표적으로 relatvie attribute rank (RAR)과 같은 방법이 있음
    - Emotion embedding space를 통해 interpolating을 수행하여 intensity를 control 할 수도 있음
    -> BUT, 분리된 학습 과정으로 인해 bias가 발생하여 여전히 낮은 합성 품질을 보임
  • 이를 해결하기 위해 intensity에 따라 emotion weight를 control 하는 conditional sampling을 활용할 수 있음
    - 특히 classifier guidance는 classifier의 graident를 사용하여 class label에 대한 sampling trajectory를 guide 할 수 있음

-> 그래서 classifier guidance와 diffusion model을 기반으로 한 soft-label guidance TTS 방식을 제시

 

• EmoDiff
  • Soft-label guidance를 활용하여 intensity control이 가능한 emotional TTS 모델
  • Emotion-unconditional acoustic model을 학습하고, emotion classifier를 모든 diffusion trajectory에 따라 학습시킴
  • 추론 시에는 specified emotion과 neutral이 $\alpha, 1-\alpha$로 설정되는 soft emotion label을 사용하여 reverse denoising process를 guide

< Overall of EmoDiff >

• Soft-label을 위해 emotion intensity를 classifier guidance에 대한 weight로 정의
• 추가적인 최적화가 필요 없고, classifier 측면에서 정밀한 intensity control이 가능
• 결과적으로 합성된 음성 품질의 저하 없이 다양한 intensity를 표현 가능

2. Diffusion Models with Classifier Guidance

- Denoising Diffusion Models and TTS Applications

• Denoising diffusion probabilistic model의 score-based interpretation에서,
  • Diffusion model은 data 분포 $p_{0}(x_{0})$를 알려진 분포 $p_{T}(x_{T})$로 변환하기 위해 forward stochastic differential equation (SDE)를 정의
    - 이때 해당하는 reverse-time을 통해 SDE는, noise에서 시작하여 sample을 합성하는 denoising process를 수행
  • 이후 neural network는 score-matching objective를 사용하여 SDE trajectory의 모든 $t \in [0,T]$에 대해 score function $\nabla_{x} \log p_{t}(x_{t})$를 추정
  • 이를 통해 diffusion model은 GAN의 instablility와 mode collapse 문제를 해결하고 sample 합성의 다양성과 높은 품질을 보장 가능
• EmoDiff는 Grad-TTS를 기반으로 함
  • Forward Process 
    1. 먼저 $x \in \mathbb{R}^{d}$를 mel-spectrogram의 frame이라 했을 때, forward SDE는:
       (Eq. 1) $dx_{t} =\frac{1}{2}\Sigma^{-1}(\mu-x_{t})\beta_{t}dt+\sqrt{\beta_{t}}dB_{t}$
       - $B_{t}$ : standard Brownian motion
       - $t \in [0,1]$ : SDE time index
       - $\beta_{t}$ : noise schedule, (이때 $\beta_{t}$는 increasing 하고 $\exp \left \{ -\int_{0}^{1}\beta_{s}ds \right\}\approx 0$)
       
    2. 그러면 $p_{1} (x_{1}) \approx \mathcal{N}(x;\mu,\Sigma)$를 얻을 수 있고, 해당 SDE는 conditional 분포 $x_{t}|x_{0}\sim\mathcal{N}(\rho(x_{0},\Sigma,\mu,t),\lambda(\Sigma,t))$를 따름
       - 이때 $\rho(\cdot), \lambda(\cdot)$는 모두 closed form
    3. 따라서 diffusion model은 $x_{0}$에서 $x_{t}$를 직접 sampling 할 수 있음
       - 실질적으로는 $\Sigma$를 identity matrix로 설정하므로 $\lambda(\Sigma, t)$는 $\lambda_{t}I$가 됨
       - 이때 $\lambda_{t}$는 known closed form
    4. 추가적으로 text에 대한 terminal 분포 $p_{1}(x_{1})$을 $\mu = \mu_{\theta}(y)$ condition 함
       - $y$ : 해당하는 frame의 aligned phoneme representation
  • Reverse Process
    1. (Eq. 1)에 대응하는 reverse-time SDE는:
       (Eq. 2) $dx_{t} = \left( \frac{1}{2}\Sigma^{-1}(\mu-x_{t})-\nabla_{x}\log p_{t}(x_{t})\right)\beta_{t}dt+\sqrt{\beta_{t}}d\tilde{B}_{t}$
       - $\nabla \log p_{t}(x_{t})$ : 추정할 score function
       - $\tilde{B_{t}}$ : reverse-time Brownian motion
    2. (Eq. 2)는 (Eq. 1)의 forward SDE와 분포 $p_{t}(x_{t})$에 대한 trajectory를 share 함
       - 따라서 (Eq. 2)를 $x_{1} \sim \mathcal{N}(\mu, \Sigma)$에서 solve 하면, sample $x_{0} \sim p(x_{0}|y)$를 얻을 수 있음
    3. 이때 neural network $s_{\theta}(x_{t}, y,t)$는 아래의 score-matching objective를 통해 score function을 추정하도록 학습됨:
       (Eq. 3) $\min_{\theta} \mathcal{L} =\mathbb{E}_{x_{0},y,t}\left[ \lambda_{t}||s_{\theta}(x_{t},y,t)-\nabla_{t}\log p(x_{t}|x_{0})||^{2}\right]$

- Conditional Sampling Based on Classifier Guidance

• Denoising diffusion model은 conditional probability $p(x|c)$를 modeling 하는 방법을 제공함
  • $c$를 class label이라 하고, unconditional generative model $p(x)$와 classifier $p(c|x)$가 있다고 하자. 이때 Bayes formula에 의해:
    (Eq. 4) $\nabla_{x}\log p(x|c)=\nabla_{x}\log p(c|x)+\nabla_{x}\log p(x)$
  • Diffusion framework가 conditional 분포 $p(x|c)$에서 sampling 하기 위해서는 score function $\nabla_{x}\log p(x_{t}|c)$가 필요함
    - 이때 classifier guidance를 통해 (Eq. 4)에 따라 classifier의 gradient를 unconditional model에 추가하는 것으로 문제를 해결할 수 있음
    
  • 실적용에서 classifier gradient는 guidance strength를 control 하기 위해 scaling 됨
    - 따라서 (Eq. 4)의 $\nabla_{x} \log p(c|x)$ 대신 $\gamma \nabla_{x} \log p(c|x)$를 사용
    - $\gamma \geq 0$ : guidance level
    - $\gamma$가 클수록 class-correlated sample이 생성되고, $\gamma$가 작을수록 sample variablity가 높아짐
  • Guidance를 위한 classifer의 input은 (Eq. 1)을 따르는 $x_{t}$를 사용함
    - 이때 time index $t$는 $[0,1]$ 내의 값을 따르므로 classifier는 $p(c|x_{t}, t)$와 같이 나타낼 수 있음
    

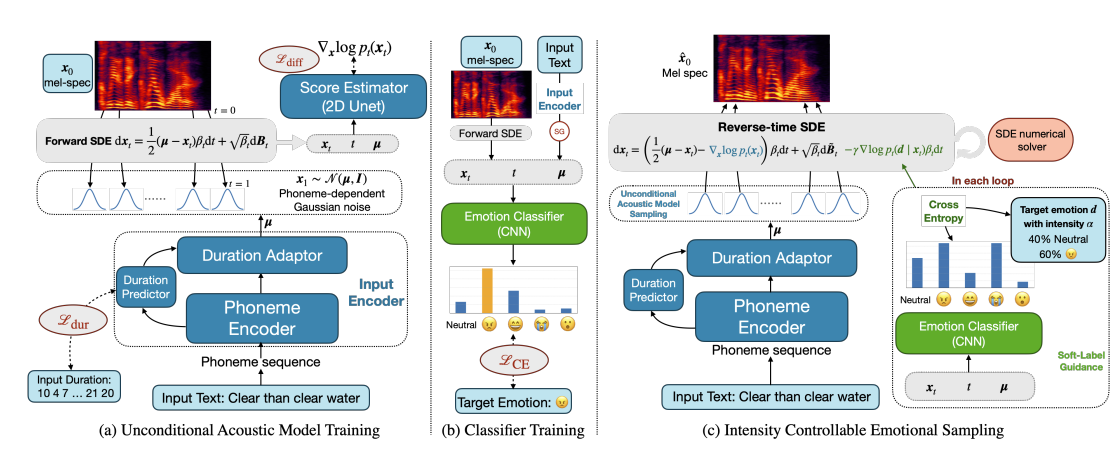
3. EmoDiff

- Unconditional Acoustic Model and Classifier Training

• EmoDiff는 unconditional acoustic model과 emotion classifier를 모두 학습해야 함
  • 이때 emotional data에 대한 diffusion acoustic model을 우선적으로 학습하지만 emotion condition은 제공되지 않음
    1. Acoustic model은 Grad-TTS를 기반으로 하고 duration modeling을 위해 forced aligner를 통해 explicit duration sequence를 제공
    2. 해당 단계에서 training objective는 $\mathcal{L}_{dur}, \mathcal{L}_{diff}$로 표현됨
       - $\mathcal{L}_{dur}$ : logarithmic duration에 대한 $\ell_{2}$ loss
       - $\mathcal{L}_{diff}$ : (Eq. 3)에 대한 diffusion loss
    3. 추가적으로 Grad-TTS와 같이 prior loss $\mathcal{L}_{prior} = -\log \mathcal{N}(x_{0};\mu,I)$를 도입하여 모델의 수렴을 도움
  • 학습이 완료되면 acoustic model은 input phoneme sequence $y$가 주어지면 $\nabla p(x_{t}|y)$와 같이 emotion label에 대해 unconditional 한 noisy mel-spectrogram $x_{t}$의 score function을 추정할 수 있음
    1. 여기서 noisy mel-spectrogram $x_{t}$에서 emotional category $e$를 분류하기 위해서는 emotion classifier가 필요
       
    2. 따라서 classifier는 text condition $y$에 대해 $p(e|x_{t},y,t)$로 공식화될 수 있음
       - 결과적으로 classifier의 input은 SDE timestamp $t$, noisy mel-spectrogram $x_{t}$, phoneme-dependent Gaussian mean $\mu$로 구성됨
    3. 이때 classifier는 standard cross-entropy loss $\mathcal{L}_{CE}$로 학습됨
       - 이를 위해 acoustic model parameter는 freeze 한 다음 emption classifier의 weight만 업데이트함

- Intensity Controllable Sampling with Soft-Label Guidance

• 우선 text $y$는 항상 필요한 condition이므로 notation을 단순화하기 위해 classifier를 $p(e|x)$라 하자
• Classifier guidance를 intensity에 따라 weight 된 emotion으로 control 할 수 있는 soft-label guidance로 확장하면
  • $m$개의 basic emotion이 있고, 모든 basic emotion $e_{i}$가 $e_{i} \in \mathbb{R}^{m}, \,\, i \in \{ 0,1,...,m-1\}$의 one-hot vector form을 가진다고 하자
    - 그러면 각 $e_{i}$에 대해 $i$-th dimension만 1을 가지고, Neutral을 위해 $e_{0}$을 사용할 수 있음
    - 따라서 $e_{i}$에 대한 intensity $\alpha$를 사용하여 weighted 된 emotion은 $d = \alpha e_{i} + (1-\alpha)e_{i}$와 같이 정의할 수 있음
  • 결과적으로 classifier $p(d|x)$에 대한 log-probability의 gradient는:
    (Eq. 5) $\nabla_{x}\log p(d|x) \triangleq \alpha \nabla_{x} \log p(e_{i}|x)+(1-\alpha)\nabla_{x}\log p(e_{0}|x)+\nabla_{x} \log p(x)$
    - 이는 instensity $\alpha$를 통한 $x$의 sampling trajectory에 대한 emotion $e_{i}$의 contribution을 나타냄
    - 따라서 $\alpha$가 크면 emotion $e_{i}$에 대해 강하게 force 된 trajectory를 따라 $x$가 sampling 되고, 그렇지 않으면 Neutral $e_{0}$을 활용하여 sampling 됨
  • 이를 기반으로 (Eq. 4)를 확장하면:
    (Eq. 6) $\nabla_{x}\log p(x|d) = \alpha \nabla_{x} \log p(e_{i}|x)+(1-\alpha)\nabla_{x}\log p(e_{0}|x)+\nabla_{x}\log p(x)$
    - Intensity $\alpha$가 1.0 (100% emotion $e_{i}$) 또는 0.0 (100% Neutral)인 경우 (Eq. 6)은 standard classifier guidance (Eq. 4)로 reduce 됨
    - 결과적으로 sampling process에서 soft-label guidance (Eq. 5)를 사용할 수 있고, intensity $\alpha$를 가지는 specified emotion $d = \alpha e_{i} + (1-\alpha) e_{0}$를 가지는 sample을 생성할 수 있음
• Intensity controllable sampling process을 위해
  1. Acoustic model을 통해 phoneme-dependent $\mu$ sequence를 얻은 다음, $x_{1} \sim \mathcal{N}(\mu,I)$를 sampling 하고, numerical simulator를 사용하여 $t=1$에서 $t=0$까지의 reverse SDE를 계산
  2. 각 simulator 업데이트에서 classifier에 current $x_{t}$를 제공하여 output probability $p_{t}(\cdot|x_{t})$를 얻은 다음, (Eq. 6)을 사용하여 guidance term을 계산
     - 이때 guidance level $\gamma$를 사용하여 guidance term을 확장
  3. 최종적으로 intensity $\alpha$를 가지는 target emotion $d$에 해당하는 $\hat{x}_{0}$를 얻음
     - 결과적으로 classifier probability와 correlate 되는 정확한 intensity를 활용할 수 있음
• 제안된 soft-label guidance는 intensity control 외에도 mixed emotion에 대한 control이 가능함
  • $d = \sum_{i=0}^{m-1} w_{i}e_{i}$가 $w_{i} \in [0,1], \, \sum_{i=0}^{m-1}w_{i}=1$에서의 모든 emotion combination을 나타낸다고 하면, (Eq. 5)는 다음과 같이 generalize 됨:
    (Eq. 7) $\nabla_{x}\log p(d|x) \triangleq \sum_{i=0}^{m-1}w_{i}\nabla_{x}\log p(e_{i}|x)$
    - 그러면 (Eq. 6)도 마찬가지로 generalize 될 수 있고, probabilistic view에 따라 interpret 할 수 있음
  • 따라서 combination weight $\{ w_{i}\}$는 basic emotion $\{ e_{i} \}$에 대한 categorical 분포 $p_{e}(\cdot)$으로 볼 수 있으므로, (Eq. 7)은 다음과 동치:
    (Eq. 8) $\nabla_{x} \log p(d|x) \triangleq \mathbb{E}_{e\sim p_{e}}\nabla_{x}\log p(e|x)$
    (Eq. 9) $\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = - \nabla_{x}CE\left[p_{e}(\cdot), p(\cdot|x)\right]$
    - $CE$ : cross-entropy function
  • (Eq. 9)는 gradient $\nabla_{x} \log p(d|x)$를 따라 sampling 할 때 target emotion 분포 $p_{e}$와 classifier output $p(\cdot |x)$의 cross-entropy가 decreasing 한다는 것을 의미
    - 따라서 cross-entropy의 gradient는 sampling process를 guide 할 수 있으므로, 해당 soft-label guidance를 통해 여러 basic emotion에 대한 weighted combination으로 complex emotion을 control 할 수 있음
  • 추가적으로 intensity $\alpha$를 사용하여 Neutral에서 target emotion $e_{i}$까지의 duration을 rescale 함
    - 이를 위해 각 emotion class $i$에 대한 mean duration $\mathbb{E}[d_{i}]$를 계산하고,
    - Output duration per phoneme을 $d_{i, \alpha} = d_{0} + \alpha(\mathbb{E}[d_{i}]-\mathbb{E}[d_{0}])$로 rescale
    - 따라서 phoneme duration도 주어진 intensity $\alpha$에 따라 control 됨

EmoDiff의 Training, Sampling 과정

4. Experiments

- Settings

• Dataset : Emotional Speech Dataset (ESD)
• Comparisons : Grad-TTS, MixedEmotion

- Results

• 합성 품질 측면에서 EmoDiff와 Grad-TTS가 가장 좋은 성능을 보임
  - 특히 MixedEmotion과 비교하면 품질 차이가 두드러지는데, 이는 EmoDiff가 MixedEmotion과 달리 intensity controllability를 위해 sample quality를 손상하지 않는다는 것을 의미

합성 품질 비교

• Emotion intensity에 따른 controllability를 비교하기 위해 classifier의 결과와 합성 품질을 비교
  - Hard condition을 사용하는 Grad-TTS와 달리 EmoDiff는 soft-guidance를 사용하여 넓은 범위의 intensity를 control 가능

Intensity에 따른 Classification Probability 비교

• Diversity에 대한 preference를 비교해 보면, anger/happy/surprise에 대해 EmoDiff가 가장 선호되는 것으로 나타남

Diversity Preference Test 결과