[Paper 리뷰] Basis-MelGAN: Efficient Neural Vocoder based on Audio Decomposition

Basis-MelGAN: Efficient Neural Vocoder based on Audio Decomposition

---

• Generative Adversarial Network (GAN) 기반의 vocoder는 autoregressive vocoder 보다는 빠른 합성이 가능하지만, 여전히 real-time으로 동작하는 것에는 한계가 있음
  - 특히 waveform length와 temporal resolution을 일치시키는 upsampling layer는 많은 시간을 소모함
• Basis-MelGAN
  • Upsampling layer의 계산량을 줄이기 위해 raw audio sample이 learned basis와 관련 weight로 decompose 함
  • Prediction target을 raw audio sample이 아닌 learned basis와 연관된 weight value로 설정함으로써 기존 upsampling layer를 간단한 network로 대체
• 논문 (INTERSPEECH 2021) : Paper Link

---

1. Introduction

• 기존의 neural vocoder는 주로 autoregressive model을 기반으로 하지만, autoregressive model은 높은 complexity와 parallelization의 어려움으로 인해 한계가 있음
  • 한편으로 WaveGlow와 같은 non-autoregressive vocoder는 GPU에서 parallelization을 가능하게 함
    1. 이때 해당 방식들은 GPU와 같은 특수한 환경에 제약되므로, 경량화를 위해서는 neural vocoder에 대한 근본적인 complexity를 줄여야 함
       - 이를 위해 LPCNet, FeatherWave와 같이 signal processing technique을 활용하는 방식들이 제안되었음
       
    2. 특히 Generative Adversarial Network (GAN) 기반의 non-autoregressive vocoder는 우수한 품질과 빠른 추론 속도를 보이고 있음
       - 대표적으로 MelGAN과 HiFi-GAN은 고품질의 음성 합성 결과를 보임
  • BUT, 이러한 GAN-based vocoder는 모델의 경량화와 빠른 속도를 달성하긴 했지만, 여전히 CPU에서 real-time audio를 합성하는 것에는 어려움이 있음
    - 특히 일부는 CPU에서 real-time으로 동작가능하더라도 합성 품질이 크게 저하됨됨
    

-> 그래서 기존 GAN-based vocoder의 computational cost를 크게 줄일 수 있는 Basis-MelGAN을 제안

 

• Basis-MelGAN
  • 모든 GAN-based vocoder에서 waveform length와 temporal resolution을 일치시키는 upsampling 작업은 상당한 computational cost를 가짐
    - 여기서 upsampling layer의 complexity는 예측할 각 window의 sample 수와 상당히 correlate 되어 있으므로 각 window의 signal을 효과적으로 represent 하면 target dimension을 줄여 complexity를 개선할 수 있음
  • 따라서 audio signal을 learned basis와 관련 weight를 사용하여 decompose 하는 방식으로 upsampling network의 complexity를 완화하고 보다 compact 한 representation을 얻음
    1. 구체적으로, 해당 decomposition에서 audio signal은 $N$ basis matrix의 non-negative weighted sum으로 나타낼 수 있고, 이때 basis는 fix 되어 있으므로 각 basis와 관련된 weight만 예측하면 됨
    2. 결과적으로 basis 수는 raw audio waveform 보다 훨씬 작으므로, output dimension을 일치하기 위해 기존보다 더 간단한 upsampling layer를 모델에 채택할 수 있음
  • Audio decomposition 측면에서, Independent Component Analysis (ICA), Time-domain Non-negative Matrix Factorization (NMF)와 같은 기존 방법을 고려할 수 있음
    - BUT, 논문에서는 network architecture에 통합할 수 있는 TasNet 기반의 audio separation model을 사용해 decomposition을 위한 basis를 얻음
  • 추가적으로 time-frequency characteristic 모델링을 향상하기 위해, multi-resolution STFT discriminator를 도입

< Overall of Basis-MelGAN >

• Upsampling layer의 계산량을 줄이기 위해 raw audio sample이 learned basis와 관련 weight로 decompose 함
• Data-driven basis representation을 얻기 위해 TasNet을 도입하고, multi-resolution STFT discriminator를 사용해 time-frequency 모델링을 수행
• 결과적으로 기존보다 빠른 추론 속도를 달성하면서 높은 합성 품질을 유지함

2. Method

• 전체적인 모델은 TasNet과 Basis-MelGAN 두 부분으로 나눌 수 있음
  1. 먼저 audio decomposition에 사용될 basis matrix를 얻기 위해 TasNet을 training 함
  2. 이후 TasNet에서 학습된 basis matrix는 Basis-MelGAN generator의 frozen parameter로 사용됨

- TasNet

• TasNet은 single-channel speech separation model으로써, $C$개의 서로 다른 source $s_{1},...,s_{c}\in\mathbb{R}^{1\times T}$의 mixture speech $x\in \mathbb{R}^{1\times T}$를 input으로 사용함
  
  • 여기서 TasNet은 mixture speech $x$로부터 $s_{1},...,s_{c}$를 추정하는 것을 목표로 함
  • 구조적으로 TasNet은 아래 그림과 같이 encoder network, separation network, 다른 network와 jointly learn 되는 basis matrix를 활용
    1. 먼저 encoder network는 1D convolution layer와 ReLU activation으로 구성됨
       
    2. Separation module은 stacked 1D dilated convolution block으로 구성된 fully convolutional network로, encoder output $\hat{\mathbf{W}}$를 separation module의 input으로 사용함
       - 여기서 Conv-TasNet을 따르는 대신, 두 mixed audio에 대해 2개의 mask $\mathbf{M}_{1},\mathbf{M}_{2}\in\mathbb{R}^{N\times \hat{T}}$를 사용함
  • TasNet의 training objective는 decomposition을 위한 audio basis를 얻는 것을 목표로 함
    - 따라서 기존과 같이 다양한 source로 separate 하지 않고, 각 audio input에 random noise를 추가한 다음 original input audio를 reconstruct 함
  • 결과적으로 TasNet의 input은 clean speech와 noise의 mixture로 구성되고, 모델은 이를 $\mathbf{M}_{1}, \mathbf{M}_{2}$의 두 mask로 separate 하도록 학습됨
    1. 이때 clean speech와 noise에 대한 weight matrix는:
       (Eq. 1) $\mathbf{W}_{i}=\hat{\mathbf{W}}\cdot \mathbf{M}_{i}$
       - $i\in\{1,2\}$ : clean speech와 noise
    2. 이후 separated $\mathbf{W}_{i}$에 basis matrix를 multiply 하여, 다음의 separated speech와 nosie signal $y_{i}$를 얻음:
       (Eq. 2) $y_{i}=\mathbf{B}\cdot \mathbf{W}_{i}$
       - $\mathbf{B}$ : size $[m,n]$의 basis matrix, $m$ : decompose 할 각 audio window length, $n$ : decomposition을 위한 basis 수
       - 일반적으로 $m \ll n$
  • 논문에서는 basis 수를 256, audio window length를 32로 설정함
    - 결과적으로 basis matrix는 $[32,256]$이고 length가 $[1,32]$인 audio의 각 window는 $[1,256]$의 weight value로 decompose 할 수 있음
    - Training objective로는 기존 TasNet과 같이 SI-SNR을 사용

TasNet Structure

- Basis-MelGAN

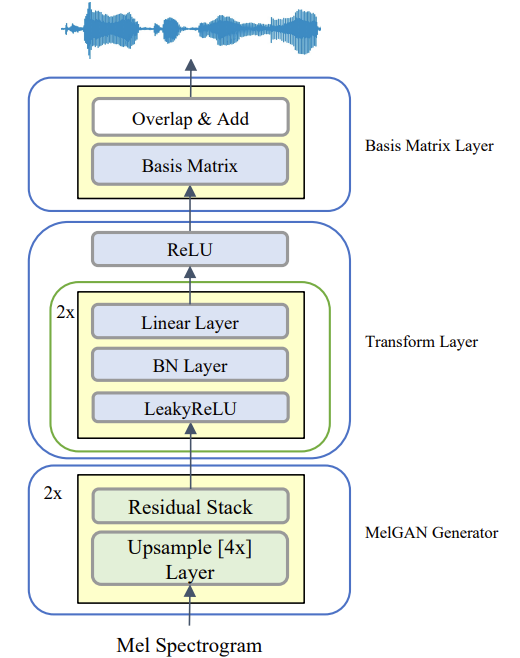
• Basis-MelGAN은 MelGAN generator, Transform layer, TasNet에서 학습된 Basis Matrix Layer로 구성되어, 아래 그림과 같이 mel-spectrogram을 input으로 하여 audio waveform을 output 함 
  • Basis-MelGAN의 generator는 MelGAN과 동일한 구조를 사용함
    - 즉, time-domain audio와 동일한 resolution을 가지도록 input mel-spectrogram을 upsampling 하는 transposed convolution layer stack으로 구성된 fully-convolutional network
    - 각 transposed convolution 다음에는 dilated convolution을 가지는 residual block stack을 추가
  • Transform layer는 linear feed-forward network로써 Leaky ReLU를 가지는 linear layer, batch normalization으로 구성됨 
  • Basis matrix layer는 TasNet basis matrix와 동일한 parameter를 share 함
    - Training 시에는 basis matrix의 parameter를 frozen 하여 사용

Basis-MelGAN Structure

- STFT Discriminator

• 논문에서는 spectrogram input을 사용하는 Multi-Resolution STFT Discriminator (MFD)를 도입함
  • 구조적으로는 MelGAN의 Multi-Scale Discriminator (MSD)와 동일한 architecture를 따르고, Parallel WaveGAN의 multi-resolution STFT loss를 사용함
    - 이러한 discriminator는 $L1$ loss function보다 더 powerful 한 criterion이므로, generator가 time-frequency characteristic을 보다 효과적으로 학습하여 frequency domain에서 더 많은 detail을 포함하도록 도움
  • 따라서 논문은 adversarial training에서 해당 MFD와 MSD를 결합함으로써 time-frequency와 speech waveform distribution을 모두 학습함
    - 한편으로 HiFi-GAN의 Multi-Period Discriminator (MPD)와 비교해 보면, MFD가 더 나은 성능을 보이고 MPD 보다 더 빠르게 동작하는 것으로 나타남
    

Multi-Resolution STFT Discriminator

- Loss Function

• Basis-MelGAN generator를 training 하기 위해 다음의 4가지 서로 다른 loss function을 사용함
  • Weight loss $L_{weight}$, multi-resolution STFT loss $L_{stft}$, multi-scale adversarial loss $L_{adv\text{_}s}$, multi-resolution STFT adversarial loss $L_{adv\text{_}f}$
    - Feature matching loss의 경우 모델이 수렴이 하지 않으므로 사용하지 않음
  • 먼저 weight loss $L_{weight}$는 TasNet의 target weight $\mathbf{W}$와 Basis-MelGAN generator의 predicted weight $\bar{\mathbf{W}}$간의 $\ell 1$ norm을 최소화함:
    (Eq. 3) $L_{weight}=|| \mathbf{W}-\bar{\mathbf{W}}||_{1}$
  • Single STFT loss $L_{single\text{_}stft}$는 TasNet의 target waveform $y$와 Basis-MelGAN generator의 predicted waveform $\bar{y}$ 간의 spectral convergence $L_{sc}$와 log STFT magnitude $L_{mg}$를 최소화함
    1. 이때 $L_{sc}, L_{mg}$의 objective는:
       (Eq. 4) $L_{sc}=\frac{|| |stft(y)|-|stft(\bar{y})| ||_{F}}{|| |stft(y)| ||_{F}}$
       (Eq. 5) $L_{mg}=\frac{1}{N}|| \log |stft(y)|-\log |stft(\bar{y})| ||_{1} $
       (Eq. 6) $L_{single\text{_}stft}=L_{sc}+L_{mg}$
       - $|stft(\cdot)|$ : magnitude를 계산하는 STFT function, $N$ : magnitude의 element 수
    2. Multi-resolution STFT loss function은 다양한 STFT parameter를 가지는 $M$개의 single STFT loss를 사용하여 계산됨:
       (Eq. 7) $L_{mr\text{_}stft}=\frac{1}{M}\sum_{m=1}^{M}L_{single\text{_}stft}^{m}$
  • Multi-scale adversarial loss $L_{adv \text{_}s}$와 multi-resolution STFT adversarial loss $L_{adv\text{_}f}$는 target waveform $y$에 대한 discriminator와 Basis-MelGAN output$\bar{y}$에 대한 discriminator output 간의 binary cross-entropy를 최소화함:
    (Eq. 8) $L_{adv\text{_}s}=\frac{1}{N_{s}}\mathrm{BCELoss}(\mathrm{MCD}(y),\mathrm{MSD}(\bar{y}))$
    (Eq. 9) $L_{adv\text{_}f}=\frac{1}{N_{f}}\mathrm{BCELoss}(\mathrm{MFD}(y),\mathrm{MFD}(\bar{y}))$
    - $N_{s}, N_{f}$ : 각각 multi-scale discriminator, multi-resolution STFT discriminator의 수
  • 결과적으로 Basis-MelGAN의 total loss $L_{G}$는:
    (Eq. 10) $L_{G}=L_{sc}+L_{mg}+L_{adv\text{_}s}+L_{adv\text{_}f}$
  • Multi-scale discriminator와 multi-resolution STFT discriminator의 training을 위해,
    1. Target waveform $y$에 대한 discriminator output과 real label 간의 binary cross-entropy $L_{dis\text{_}real}$를 최소화하고:
       (Eq. 11) $L_{dis\text{_}real} =\frac{1}{N}\mathrm{BCELoss}(D(y),1)$
    2. Basis-MelGAN output $\bar{y}$과 fake label에 대한 discriminator output의 binary cross-entropy $L_{dis\text{_}fake}$를 최소화함:
       (Eq. 12) $L_{dis\text{_}fake} =\frac{1}{N}\mathrm{BCELoss}(D(\bar{y}),0)$
       - $N$ : multi-scale discriminator / multi-resolution STFT discriminator 수, $D$ : MFD 또는 MSD
       - $1$ : real label, $0$ : fake label

3. Experiments

- Settings

• Dataset : LJSpeech
• Comparisons : HiFi-GAN, Multi-Band MelGAN

- Results

• MOS 측면에서 Basis-MelGAN은 우수한 합성 성능을 달성함

합성 성능 비교

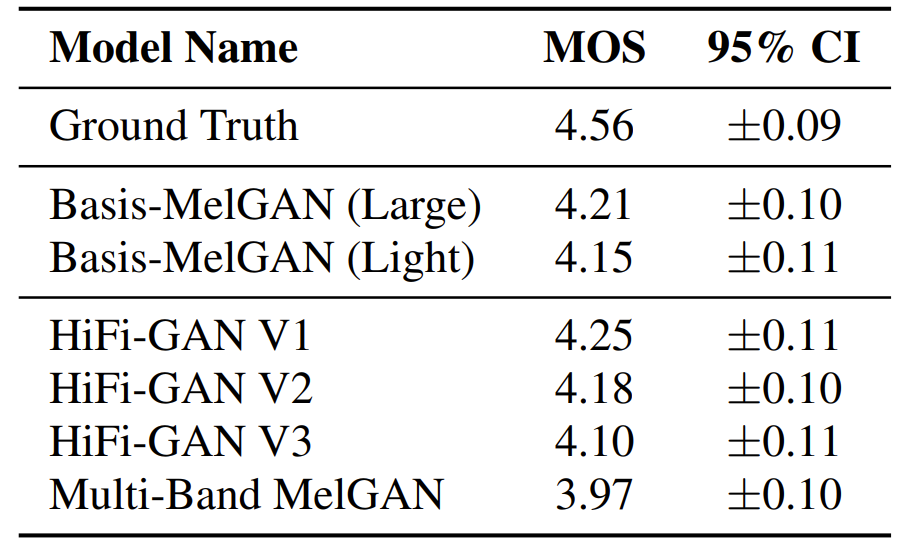
• 추가적으로 Tacotron2를 활용하여 Text-to-Speech pipeline에 각 vocoder를 적용해 보면, 마찬가지로 Basis-MelGAN이 우수한 성능을 보임

Tacotron2에 적용했을 때의 합성 성능

• 추론 속도 측면에서도 Basis-MelGAN은 가장 빠른 RTF를 달성함

추론 속도 비교