[Paper 리뷰] Continuous Autoregressive Modeling with Stochastic Monotonic Alignment for Speech Synthesis

Continuous Autoregressive Modeling with Stochastic Monotonic Alignment for Speech Synthesis

---

• Speech synthesis를 위해 autoregressive modeling을 활용할 수 있음
• CAM
  • Multi-modal latent space를 가지는 Variational AutoEncoder, conditional probability distribution으로써 Gaussian Mixture Model을 활용하는 autoregressive model을 활용
  • 특히 Variational AutoEncoder의 latent space에서 continuous speech representation을 통해 training/inference pipeline을 simplifying
  • Strict monotonic alignment를 enforce 하기 위해 stochastic monotonic alignment mechanism을 적용
• 논문 (ICLR 2025) : Paper Link

---

1. Introduction

• Text-to-Speech (TTS)에서 autoregressive (AR) modeling을 위해서는 일반적으로 2-stage training을 주로 채택함
  • First stage에서는 VQ-VAE에 기반한 vector quantization bottleneck을 통해 input data를 discrete latent representation으로 변환함
    - Second stage에서는 encoder에서 생성된 discrete latent code에 대해 AR model을 training 함
  • 이때 AR model은 latent space에서 sequential dependency를 capture 하여 previous latent code를 기반으로 next latent code를 predict 하는 방법을 학습함 
    1. 특히 FastSpeech2와 같은 non-autoregressive model과 비교하여 AR model은 acoustic vector와 duration을 simultaneously modeling 할 수 있다는 장점이 있음
    2. 추가적으로 prompt를 통해 speaker style에 대한 in-context learning을 지원할 수 있음
  • BUT, AR model을 통해 audio signal을 faithfully reconstruct 하려면 상당히 큰 codebook size가 필요하고, discrete code 사용 시에는 artifact와 mispronunciation이 발생함 
    1. 특히 codebook은 Straight-Through (ST) estimator를 주로 사용하기 때문에 training unstability가 발생함
    2. SoundStream, DAC와 같이 Residual Vector Quantization (RVQ)를 활용한 multiple codebook을 도입하면 해당 문제를 어느 정도 해결할 수 있지만, specialized second-stage model이 필요하다는 단점이 있음
       - 따라서 extra codebook으로 인한 computational overhead를 해결하기 위해 VALL-E, MusicGen 등의 기존 AR model은 modeling 과정에서 모든 token을 사용하지 않음

-> 그래서 speech synthesis task에서 continuous AR modeling을 지원할 수 있는 CAM을 제안

 

• CAM
  • Multi-modal latent constraint로 speech를 compress 하는 Gaussian Mixture Model-Variational AutoEncoder (GMM-VAE) model을 활용
  • 이후 text에 따라 compressed acoustic vector를 autoregressively modeling 하는 Gaussian Mixture Model-Language Model (GMM-LM)을 도입
    - 이때 continuous AR modeling을 통해 recover 함
  • 추가적으로 encoder, decoder를 strictly monotonic fashion으로 align 하는 attention mechanism을 적용

< Overall of CAM >

• Multi-modal latent distribution을 가지는 VAE와 continuous AR modeling을 활용한 TTS model
• 결과적으로 기존보다 뛰어난 합성 품질을 달성

VALL-E vs. CAM

2. Autoregressive Modeling with Continuous Neural Speech Codec

- Learning Continuous Speech Codecs with Gaussian Mixture Models VAE

• Variational AutoEncoder (VAE)는 generative model을 학습하고 data compression을 수행하기 위한 general framework를 제공함
  • 먼저 $\mathbf{x}$를 VAE input, $\mathbf{z}$를 latent code라고 할 때, VAE는 다음의 Evidence Lower BOund (ELBO) objective를 optimize 함:
    (Eq. 1) $\mathcal{L}=\mathbb{E}_{q(\mathbf{z}|\mathbf{x})}\left[\log p(\mathbf{x}|\mathbf{z})\right]-\text{KL} \left(q(\mathbf{z}|\mathbf{x})||\mathcal{N}(0,I)\right)$
    - $\mathbb{E}_{q(\mathbf{z}|\mathbf{x})}\left[\log p(\mathbf{x}|\mathbf{z})\right]$ : reconstructed data의 log-likelihood
    - $\text{KL} \left(q(\mathbf{z}|\mathbf{x})||\mathcal{N}(0,I)\right)$ : latent distribution이 standard Gaussian과 close 하도록 encourage 하는 KL-divergence term으로써, meaningful latent space를 보장하는 regularization mechanism으로 동작함
  • VQ-VAE에서 continuous latent variable $\mathbf{z}$는 $K$ possible entry가 있는 learned codebook의 index에 해당하는 discrete latent code $z$로 replace 됨
    1. 여기서 각 codebook entry는 $D$-dimensional vector $\mathbf{v}$에 해당함
    2. VQ-VAE는 decoding 시 latent distribution에서 sampling 하지 않고 input을 quantize 하여 continuous encoder output을 nearest discrete code에 mapping 함
    3. VAE encoder의 output을 $\mathbf{h}=E(\mathbf{x})$라고 하면, posterior는:
       (Eq. 2) $q(z=k|\mathbf{x})=\left\{\begin{matrix}
       1, & \text{if}\,\,k=\arg\min_{b}||\mathbf{h}-\mathbf{v}_{b}||_{2} \\
       0, & \text{otherwise} \\
       \end{matrix}\right.$
       - $E(\cdot)$ : convolutional layer로 구성된 encoder
  • Qunatization은 gradient backpropagation을 방해하는 non-differentiable operation이므로 decoder에서 encoder로 gradient를 전달하기 위해 Straight-Through estimator를 사용함
    1. 즉, 다음과 같이 vector quantization objective (codebook loss)와 commitment loss가 추가됨:
       (Eq. 3) $\mathcal{L}=\log p(\mathbf{x}|z_{q})+\beta||z_{e}-\text{sg}(z_{q})||_{2}^{2}+||\text{sg}(z_{e})-z_{q}||_{2}^{2},$
       $\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \text{where}\,\,\, z_{q}(\mathbf{x})=\mathbf{v}_{k},\,\,k=\arg\min_{b}||E(\mathbf{x})-\mathbf{v}_{b}||_{2}$
       - $\text{sg}$ : stop-gradient operator
       - 이때 기존 VAE와 달리 prior $p(\mathbf{z})$는 uniform 하다고 가정하므로 KL-divergence는 constant 해 학습에 영향을 주지 않고, vector quantization을 통해 regularization이 수행됨
    2. Quantization은 training 중에 categorical distribution을 implicitly define 하여, autoregressive model이 prior/latent distribution을 recover 하는 방식으로 학습되는 second-stage를 allow 함
       - BUT, SoundStream과 같은 discrete audio code의 경우 codebook size가 상당히 커질 수 있고, decoding 중에 mispronunciation이 나타날 수 있음
  • 따라서 논문은 quantization에 의존하지 않고 multi-modal latent space를 지원하는 VAE compression model을 활용함
    1. 이는 VAE stage가 second-stage에서 recover 할 수 있는 valid latent distribution을 정의하는 한, quantization 외의 option을 사용할 수 있다는 것에 기반함
    2. 즉, 논문은 VAE stage에서 generative model을 구축하지 않으므로 deterministic mapping을 사용하고 (Eq. 2)의 quantization step을 skip 함
       - 그러면 posterior는 $q(\mathbf{h}|\mathbf{x})=\delta(\mathbf{h}-E(\mathbf{x}))$와 같이 얻어짐
       - $\delta$ : Dirac-delta function
  • 한편으로 VQ로 정의된 categorical distribution은 multi-modal distribution을 modeling 할 수 있음
    1. 따라서 parameter가 $\{\pi_{l},\mu_{l},\sigma_{l}\}_{l=1}^{L}$인 Gaussian prior의 learned mixture를 사용하여 continuous latent distribution이 multi-modal이 되도록 allow 함
    2. 여기서 해당 setting에 대한 ELBO는:
       (Eq. 4) $\mathcal{L}=\mathbb{E}_{q(\mathbf{h}|\mathbf{x})}\left[\log p(\mathbf{x}|\mathbf{h})\right]-\lambda \text{KL}\left(q(\mathbf{h}|\mathbf{x})||\sum_{l=1}^{L}\pi_{l}\mathcal{N}(\mu_{l},\Sigma_{l})\right)$
       - $\lambda$ : regularization strength를 control 하는 역할
       - $l$ : mixture index, $L$ : total mixture 수
    3. 해당 posterior는 deterministic function이고 prior는 Gaussian mixture이므로 KL-divergence에 대한 analytical solution이 존재하지 않음
       - 대신 Monte-Carlo estimation을 통해 KL-divergence를 compute 함
  • 결과적으로 논문은 앞선 GMM constraint로 training 된 VAE를 GMM-VAE로써 활용함
    - 특히 speech signal에 대해 GMM-VAE를 training 할 때, reconstruction term을 mel-spectrogram reconstruction loss로 replace 하고 EnCodec, DAC를 따라 discriminator를 추가함

(좌) Residual Vector Quantization Codec (우) GMM-VAE Speech Codec

- Autoregressive Speech Modeling with GMM-LM

• Autoregressive model은 discrete input/output을 사용하는 transformer를 주로 활용함
  • 먼저 timestep $t$에서의 conditional probability는:
    (Eq. 5) $P(z_{t}|z_{t-1},z_{t-2},...,z_{1},Y)=\text{Categorical}\left(f(z_{t-1},z_{t-2},...,z_{1},Y)\right)$
    - $f()$ : previous prediction $z_{t-1},z_{t-2},...,z_{1}$과 conditioning information $Y$를 사용하여 next token을 predict 하는 neural network로써, standard cross-entropy loss로 training 됨
    - 여기서 autoregressive model의 conditional probability는 previous token에 따라 condition 되고 vaild distribution을 생성하는 한, categorical distribution을 반드시 따를 필요는 없음
  • 따라서 논문은 continuous random variable $\mathbf{h}_{t}\in \mathbb{R}^{D}$에 대한 autoregressive model을 고려함
    1. 이때 conditional probability는 Gaussian mixture로 represent 될 수 있음:
       (Eq. 6) $p(\mathbf{h}_{t}|\mathbf{h}_{t-1},...,\mathbf{h}_{1},Y)=\sum_{n=1}^{N}\omega_{n}^{t}\mathcal{N}\left( \mathbf{h}_{t};\nu_{n}^{t}(\tau_{n}^{t})^{2}\right)$
       - $\omega_{n}^{t},\nu_{n}^{t},\tau_{n}^{t}$ : 각각 $n$-th mixture의 weight, mean, frame $t$에서의 diagonal variance
    2. Mixture parameter는 previous input, conditioning information을 사용하는 neural network $f()$에 의해 생성됨:
       (Eq. 7) $\left[\omega_{1}^{t},...,\omega_{N}^{t},\nu_{1}^{t},...,\nu_{N}^{t},\tau_{1}^{t},...,\tau_{N}^{t}\right] =f(\mathbf{h}_{t-1},...,\mathbf{h}_{1},Y)$
  • 한편으로 mixture weight, variance가 valid 함을 보장하기 위해 softmax를 적용하여 $\omega_{n}^{t}$를 normalize 하고 softplus를 network output의 $\tau_{n}^{t}$에 적용할 수 있음
    1. Gaussian mixture autoregressive modeling의 경우, embedding layer나 softmax layer가 필요하지 않음
    2. Continuous model의 경우 stop token이 존재하지 않으므로 stop token을 predict 하기 위한 additional linear classifier가 필요함
  • 최종적으로 autoregressive model은 Conformer Encoder-Decoder architecture를 기반으로 구축되고, 논문은 해당 Gaussian Mixture Model-based Autoregressive model을 GMM-LM으로써 사용함

(좌) VALL-E (우) GMM-LM

- Stochastic Hard Monotonic Alignment Learning

• Speech synthesis에서 monotonic alignment는 word error rate를 낮추고 naturalness를 향상할 수 있음
  • 여기서 monotonic alignment mechanism은 encoder state $j$와 decoder state $i$ 간의 energy $e_{i, j}$가 주어졌을 때, 다음과 같이 sigmoid function을 통해 alignment probability를 얻음:
    (Eq. 8) $p_{i,j}=\text{Sigmoid}(e_{i,j})$
  • Dot product를 사용하는 경우, $p_{i,j}$를 parallel compute 할 수 있지만 monotonic constraint를 enforce 하지 않음
    1. Monotonic attention을 적용하기 위해 iterative process를 활용하여 $p_{i,j}$에서 attention scroe를 compute 함:
       (Eq. 9) $\alpha_{i,j}=\alpha_{i-1,j-1}(1-p_{i,j-1})+\alpha_{i-1,j}p_{i,j}$
       - $\alpha_{i,j}$ : encoder state를 sum up하는데 사용되는 attention weight
    2. $\alpha_{i,j}$ expectation은 monotonic 하지만 모든 alignment step이 각 sample의 monotonic constraint를 strictly follow 하지 않음
       - 이를 위해 training 중에 binary $p_{i,j}$를 encourage하는 Gaussian noise를 energy term에 adding할 수 있음
       - BUT, 해당 approach는 optimization 과정에서 bias를 반영하고 training/test discrepancy로 인해 성능 저하가 발생할 수 있음
    3. 따라서 논문은 forward pass에서 soft $p_{i,j}$를 Bernoulli distribution에서 sampling 된 binary value $u_{i,,j}^{\text{forward}}$로 replace 하여 사용함:
       (Eq. 10) $u_{i,j}^{\text{forward}}\sim\text{Bernoulli}(p_{i,j})$
       - 이를 통해 attention weight를 always binary로 보장할 수 있음
  • Backpropagation을 위해 Bernoulli distribution의 Gumble-Softmax relaxtion을 사용하여 gradient를 approximate 함:
    (Eq. 11) $u_{i,j}^{\text{backward}}=\frac{\exp((\log(p_{i,j})+g_{1})/s)}{\exp((\log(p_{i,j})+g_{1})/s) + \exp((\log(1-p_{i,j})+g_{2})/s )}$
    - $g_{1},g_{2}\sim\text{Gumble}(0,1)$, $s$ : relaxtion degree를 control 하는 temperature parameter
    - 이때 Training end에서 $s$를 gradually decrease 하도록 schedule을 설정함

GMM-LM Monotonic Alignment

3. Experiments

- Settings

• Dataset : LibriSpeech
• Comparisons : VALL-E, StyleTTS2, HierSpeech++

- Results

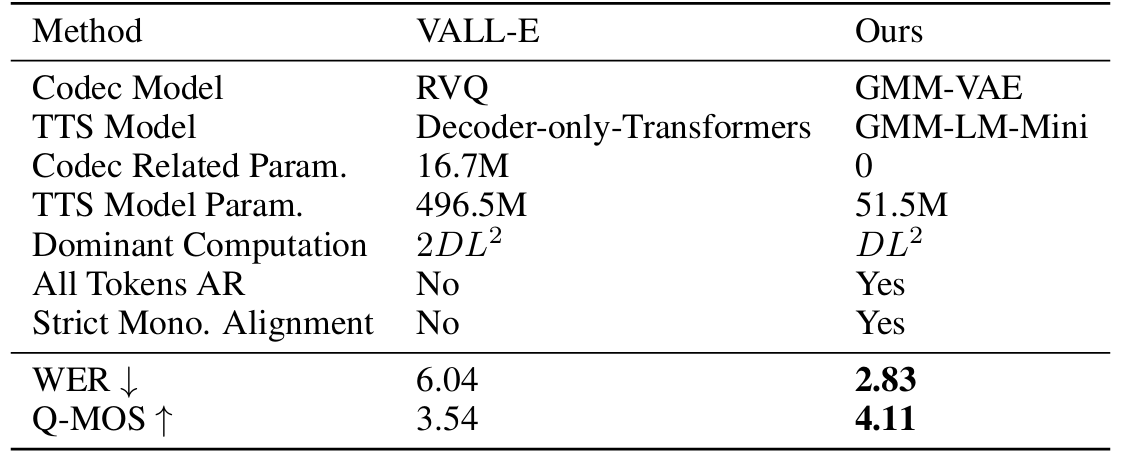
• 전체적으로 CAM의 합성 품질이 가장 뛰어남

성능 비교

• Mel-Spectrogram vs. GMM-VAE Features
  • GMM-LM의 성능이 mel-spectrogram feature로 학습된 model 보다 더 우수함
  • Model size를 늘리는 경우 GMM-based와 Mel-based 간의 gap을 줄일 수 있지만 computation cost도 같이 증가함
  • 추가적으로 mel-based model의 경우 GMM-VAE feature 보다 proper alignment를 달성하는데 더 긴 시간이 필요함

Mel-Spectrogram vs. GMM-VAE

• Reconstruction Quality of Discrete and Continuous Codecs
  • GMM-VAE가 EnCodec 보다 speech reconstruction 측면에서 더 효과적임

GMM-VAE vs.EnCodec

• Ablation Study
  • Speech codec을 training 할 때 quantization을 수행하지 않으므로 (Eq. 4)의 divergence constraint는 latent distribution에 directly influence 함
  • 이때 divergence constraint가 없으면 downstream GMM-LM을 succesfully training 하기 어려움

$\lambda$에 따른 Reconstruction Quality

• GMM-LM Parammeterization
  • 6-Mixture를 사용하는 경우 최적의 성능을 달성할 수 있음

Mixture 수에 따른 성능 비교