[Paper 리뷰] Harmonic WaveGAN: GAN-based Speech Waveform Generation Model with Harmonic Structure Discriminator

Harmonic WaveGAN: GAN-based Speech Waveform Generation Model with Harmonic Structure Discriminator

---

• Speech waveform을 합성하기 위해 Generative Adversarial Network-based model을 활용할 수 있음
• Harmonic WaveGAN
  • Time/frequency domain에 대한 2개의 discriminator를 사용해 speech waveform의 characteristic을 capture 함
  • 특히 Harmonic Structure Discriminator는 harmonic convolution을 기반으로 harmonic structure를 모델링함
• 논문 (INTERSPEECH 2021) : Paper Link

---

1. Introduction

• Text-to-Speech (TTS)에서는 neural vocoder를 사용하여 waveform을 생성할 수 있음
  • 기본적으로 nerual vocoder로써 sample-by-sample autoregressive model을 고려할 수 있지만, 느린 추론 속도로 인해 한계가 있음
    - 따라서 Flow-based, Diffusion-based, Generative Adversarial Network (GAN)-based와 같은 non-autoregressive model들이 도입됨
  • 특히 Parallel WaveGAN은 waveform generator와 discriminator를 adversarially training 하는 대표적인 GAN-based vocoder임
    1. BUT, Parallel WaveGAN은 빠른 추론 속도에 비해 high-frequency에서 artificial trace가 발생하는 경향이 있음
       
    2. 한편으로 GAN-based model에서 discriminator는 naturalness 향상에 중요한 역할을 함
       - 실제로 Multi-band MelGAN은 서로 다른 frequency band에서 동작하는 multiple discriminator를 도입했고, HiFi-GAN은 periodic feature를 capture 하는 discriminator를 도입함
       - 즉, discriminator에서 speech waveform의 characteristic을 직접적으로 capture 하도록 하면 vocoder의 성능을 향상할 수 있음

-> 그래서 harmonic structure를 capture 하는 discriminator를 도입한 Harmonic WaveGAN을 제안

 

• Harmonic WaveGAN
  • Time domain discriminator와 Harmonic structure discriminator의 2가지 discriminator를 활용
  • 이때 Harmonic structure discriminator는 adjacent frequency가 아닌 harmonic series의 basis에서 정의되는 Harmonic convolution으로 구성됨
    
  • 전체적인 구조는 Parallel WaveGAN을 기반으로 하여 빠른 추론 속도를 유지하면서 음성 합성 품질을 향상

< Overall of Harmonic WaveGAN >

• Parallel WaveGAN을 기반으로 Time domain discriminator와 Harmonic structure discriminator를 도입
• 결과적으로 빠른 추론 속도를 유지하면서 distinct 한 harmonic structure를 효과적으로 capture 가능

2. Parallel WaveGAN

• Parallel WaveGAN은 generator로 non-autoregressive WaveNet-based model을 사용하여 adverasially training 됨
  • 이때 Parallel WaveGAN은 non-autoregressive model을 통해 sample을 병렬적으로 생성하고, 추론 속도 향상이 가능
    
  • 한편으로 generator는 adversarial loss 외에 auxiliary loss로써 multi-resolution STFT loss를 활용함
    1. 해당 multi-resolution STFT loss는 target과 예측된 waveform의 frequency domain에 대한 STFT 차이로써 계산됨
    2. 그러면 generator는 multi-resolution STFT loss $L_{STFT}$와 adversarial loss $L_{adv}$를 결합한 generator loss $L_{G}$를 최소화하도록 training 됨:
       (Eq. 1) $L_{G}(G,D)=L_{STFT}(G)+\lambda_{adv}L_{adv}(G,D)$
       - $\lambda_{adv}$ : balancing parameter
    3. 여기서 adversarial loss $L_{adv}$는:
       (Eq. 2) $L_{adv}(G,D)=\mathbb{E}_{z\sim p_{z}}[(1-D(G(z,h)))^{2}]$
       - $z$ : input noise, $p_{z}$ : Gaussian distribution $\mathcal{N}(0,I)$, $h$ : conditional acoustic feature
  • Discriminator는 다음의 discriminator loss $L_{D}$를 최소화하도록 training 됨:
    (Eq. 3) $L_{D}(G,D)=\mathbb{E}_{x\sim p_{data}}[(1-D(x))^{2}]+\mathbb{E}_{z\sim p_{z}}[D(G(z,h))^{2}]$
    - $x$ : target speech waveform, $p_{data}$ : target waveform의 distribution
  • 결과적으로 Parallel WaveGAN은 generator를 adversarial loss와 multi-resolution STFT loss의 합으로 training 함으로써, 적은 parameter 수로 높은 합성 품질을 달성함

3. Harmonic Convolution

• Speech waveform의 frequency는 harmonically related 되어 있고, 해당 harmonic structure는 human perception에 큰 영향을 미침
  • 특히 Harmonic convolution은 adjacent frequency가 아닌 harmonic series에 기반한 convolution kernel을 통해 acoustic signal의 harmonic structure를 효과적으로 capture 할 수 있음
  • 따라서 $\omega$를 frequency index, $\tau$를 time index로 가지는 STFT spectrogram $X(\omega, \tau)$가 주어지면, $X(\omega, \tau)$의 harmonic convolution은:
    (Eq. 4) $Y_{n}(\hat{\omega},\hat{\tau})=\sum_{k=1}^{K_{f}}\sum_{\tau=1}^{K_{t}}X\left(\frac{k\hat{\omega}}{n},\hat{\tau}-\tau\right)K(k,\tau)$
    (Eq. 5) $Y(\hat{\omega},\hat{\tau})=\sum_{n=1}^{N}\omega_{n}Y_{n}(\hat{\omega},\hat{\tau})$
    - $K(\cdot, \cdot)$ : harmonic convolution의 kernel, $K_{t}, K_{f}$ : 각각 time/frequency axis에 대한 kernel size
    - $n$ : $\hat{\omega}/n$을 base frequency로 하는 convolution을 계산하기 위한 anchor
    - 해당 anchor $n$을 사용하면 base frequency $\hat{\omega}$의 정수배 harmonic series와 base frequency $\hat{\omega}/n$의 $1/n$배 harmonic series를 capture 할 수 있음
  • 한편으로 Harmonic convolution은 frequency axis를 따라 convolution 계산을 위한 discrete data에 access 하기 위해 inefficient computation이 필요하므로 전체 computation time이 늘어남
    1. 해당 문제를 해결하기 위해, multi-dimensional array를 matrix로 변환하여 complex looping을 회피하고 computation time을 개선하는 Harmonic lowering method를 고려할 수 있음
    2. 추가적으로 frequency domain을 logarithm으로 capture 하면 Harmonic convolution을 더 빠르게 계산할 수 있고, 이때 $X(\omega, \tau)$에 대한 Logarithmic harmonic lowering은:
       (Eq. 6) $X'_{n}(k,\hat{\omega},\hat{\tau})=X\left(\log \frac{k\hat{\omega}}{n},\hat{\tau}\right)=X\left(\log \frac{k}{n}+\log \hat{\omega},\hat{\tau}\right)$
       (Eq. 7) $K'(k,1,\tau)=K(k,\tau)$
       (Eq. 8) $Y_{n}(\hat{\omega},\hat{\tau})=\sum_{k=1}^{K_{f}}\sum_{\omega=1}^{1}\sum_{\tau=1}^{K_{t}}X'(k,\hat{\omega},\hat{\tau}-\tau)K'(k,\omega,\tau)$
  • 위를 통해 $X$를 $X'_{n}$으로 변환함으로써, frequency domain의 harmonic strucute에 continuously access 할 수 있음
    - 결과적으로 Harmonic convolution은 기존 2D convolution과 동일한 방식으로 계산됨

Overall of Harmonic WaveGAN

4. Harmonic WaveGAN

• 기존의 Parallel WaveGAN은 합성된 waveform을 time domain에서 target과 일치시키는 것을 목표로 함
  • BUT, time domain resemblance 대신에 합성된 waveform을 frequency domain의 target과 일치시키면 더 나은 representation을 얻을 수 있음
    - 특히 이를 통해 human perception에 영향을 미치는 harmonic structure에 집중할 수 있고, 보다 natural 한 음성 합성이 가능함
  • 따라서 제안하는 Harmonic WaveGAN은 Parallel WaveGAN을 기반으로 waveform의 harmonic structure를 capture 하도록 설계됨
    1. 이때 아래 그림과 같이 time domain과 harmonic structure에 대한 2가지 discriminator를 사용
    2. 먼저 time domain discriminator는 기존 Parallel WaveGAN discriminator와 동일하게 1D dilated convolution layer를 활용하고 speech waveform을 input으로 함
    3. Harmonic structure discriminator는 speech waveform의 STFT를 input으로 하고, Logarithmic harmonic lowering에 기반한 Harmonic convolution과 2D convolution layer로 구성됨
       - Input complex STFT coefficient는 2개의 separate real-valued channel로 처리됨
       - Harmonic convolution 다음의 2D convolution layer는 time과 frequency direction 모두에서 receptive field를 expand 하기 위해 dilate 됨
  • 이때 Harmonic WaveGAN의 generator loss는 (Eq. 1)과 동일하고, harmonic structure discriminator loss $L_{HS}$는:
    (Eq. 9) $L_{HS}=\mathbb{E}_{x\sim p_{data}}[(1-D_{HS}(x))^{2}]+\mathbb{E}_{z\sim p_{z}}[D_{HS}(G(z,h))^{2}]$
    - $D_{HS}$ : harmonic structure discriminator로 해당 output은 batch size, channel, frequency, time의 4가지 dimension을 가짐
  • 결과적으로 discriminator loss $L_{D}$는 time domain과 harmonic structure discriminator loss를 결합하여 얻어짐:
    (Eq. 10) $L_{D}= (L_{TD}+\lambda_{har}L_{HS})/2$
    - $L_{TD}$ : time domain discriminator loss로써 (Eq. 3)을 따름, $\lambda_{har}$ : balancing parameter

Harmonic WaveGAN의 Discriminator

5. Experiments

- Settings

• Dataset : JSUT, JVS
• Comparisons : Parallel WaveGAN

- Results

• MOS 측면에서 Harmonic WaveGAN은 Parallel WaveGAN보다 높은 성능을 보임
  - 추가적으로 harmonic convolution을 제거하는 경우 성능 저하가 발생하는 것으로 나타남

MOS 비교

• Mel-spectrogram 측면에서 Harmonic WaveGAN은 high-frequency range에서도 harmonic structure를 명확하게 나타냄

Mel-spectrogram 비교 (a) Target Speech (b) Parallel WaveGAN (c) Harmonic WaveGAN

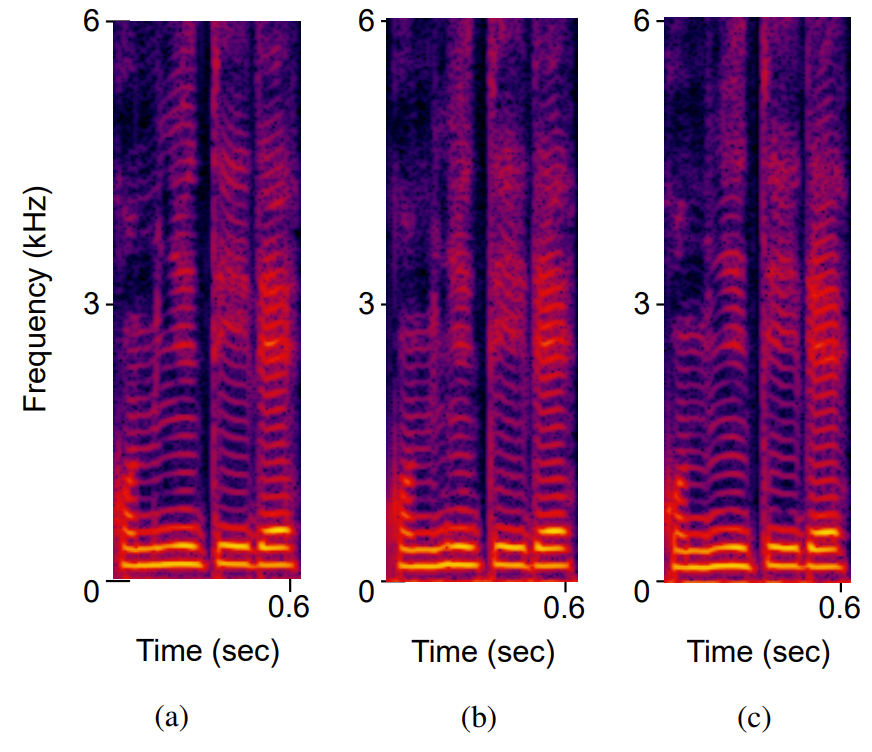
• TransformerTTS 모델을 기반으로 각 vocoder를 TTS 작업에 적용해 보면, 마찬가지로 Harmonic WaveGAN을 사용했을 때 가장 좋은 성능을 보임

TTS 모델에서의 결과