[Paper 리뷰] FIRNet: Fundamental Frequency Controllable Fast Neural Vocoder with Trainable Finite Impulse Response Filter

FIRNet: Fundamental Frequency Controllable Fast Neural Vocoder with Trainable Finite Impulse Response Filter

---

• Fundamental frequency를 control 할 수 있는 neural vocoder는 우수한 합성 품질을 보이지만, 여전히 signal processing에 기반한 기존 vocoder들보다 느린 추론 속도를 가짐
• FIRNet
  • Trainable time-variant Finite Impulse Response (FIR) filter를 갖춘 source-filter model을 활용
  • Neural network를 통해 multiple FIR coefficient를 예측하고, mixed excitation signal을 해당 FIR coefficient와 convolution 하여 waveform을 형성함
• 논문 (ICASSP 2024) : Paper Link

---

1. Introduction

• Neural vocoder는 acoustic feature를 고품질 waveform으로 변환하는 것을 목표로 함
  • 특히 text-to-speech (TTS), voice conversion 등의 task에서 효과적으로 사용하기 위해서는 fundametnal frequency $f_{0}$ controllability와 real-time generation speed가 요구됨
    1. 대표적으로 HiFi-GAN은 high-fidelity neural vocoder로써 가장 널리 활용되고 있지만, flexible $f_{0}$ controllability가 부족함
    2. 이를 해결하기 위해 Source-Filter HiFi-GAN (SiFi-GAN)은 quasi-periodic (QP) architecture를 활용한 source network와 HiFi-GAN module을 활용하는 filter network를 제시했음
       - 결과적으로 SiFi-GAN에서 source network는 $f_{0}$-dependent sine signal을 waveform에 대한 source excitation representation으로 변환하는 방식을 사용
  • BUT, SiFi-GAN과 같은 기존의 neural source filter는 flexible $f_{0}$ controllability를 제공할 수 있지만, filtering process의 high-complexity로 인해 속도가 느림

-> 그래서 높은 $f_{0}$ controllability와 빠른 추론 속도를 보장하는 neural source filter model인 FIRNet을 제안

 

• FIRNet
  • Source-filter model에서 source excitation signal과 vocal tract의 impulse response를 convolving 하여 speech waveform을 생성할 수 있음
    - 즉, neural network를 사용하여 적절한 impulse response를 추정함으로써 high-speed neural source-filter-based vocoder를 구성하는 것이 가능
  • 이를 위해 trainable time-variant Finite Impulse Response (FIR) filter를 활용해 $f_{0}$-independent acoustic feature를 multiple FIR coefficient로 변환함
  • 이후, 해당 FIR coefficient로 source excitation signal을 filtering 하여 intermediate residual signal을 통해 speech waveform을 생성함
    - 이때 FIR filter는 $f_{0}$ parameter에 의존하지 않기 때문에 source excitation signal을 변경하는 것으로 flexible $f_{0}$ control이 가능하고, 모델은 simple linear filtering으로 인해 낮은 complexity를 가짐

< Overall of Paper >

• Trainable time-variant Finite Impulse Response (FIR) filter를 갖춘 source-filter model을 활용
• Neural network를 통해 multiple FIR coefficient를 예측하고, mixed excitation signal을 해당 FIR coefficient와 convolution 하여 waveform을 생성
• 결과적으로 빠른 추론 속도와 뛰어난 $f_{0}$ controllability를 달성

2. Method

• FIRNet은 아래 그림과 같이, (a) excitation generator, (b) 3개의 causal convolution block, (c) residual FIR network와 resonance FIR network로 구성됨
  • Input feature로는 continuous $f_{0}$, voiced/unvoiced flag (V/UV), band aperiodicity (BAP), mel-generalized cepstrum coefficient (MGC)를 사용
  • 추론 시에는,
    1. Excitation generator가 먼저 continuous $f_{0}$, V/UV, BAP를 사용하여 mixed excitation signal을 생성함
       - 이때 BAP와 MGC는 causal convolution block에 의해 latent representation으로 변환됨
       - Residual FIR network에 대한 latent representation은 BAP와 MGC latent representation을 통해 얻어짐
    2. Mixed excitation signal의 characteristic은 실제 residual signal과 다르기 때문에, 해당 latent representation으로 condition 된 residual FIR network는 mixed excitation signal을 residual signal로 변환함 
    3. 최종적으로 residual signal은 MGC latent representation으로 condition 된 resonance FIR network에 의해 speech waveform으로 변환됨 

Overall of FIRNet

- Details of Generator Modules

• Excitation Generator
  • Excitation generator는 mixed excitation signal을 생성하는 역할로, $f_{0}$-dependent pulse train과 BAP 기반의 Gaussian noise의 weighted sum으로 구성됨
  • 결과적으로 $t$-th mixed excitation signal $s(t)$는:
    (Eq. 1) $s(t)=\left\{\begin{matrix}
    g_{p}v^{(k)}*p(t)+g_{n}u^{(k)}*n(t), & \text{if voiced}\\
    g_{n}n(t), & \text{if unvoiced} \\
    \end{matrix}\right.$
    - $p(t), n(t), g_{p}, g_{n}$ : 각각 $f_{0}$-dependent pulse train, time $t$의 Gaussian noise, $p(t)$에 대한 gain value, $n(t)$에 대한 gain value
    - $v^{(k)}, u^{(k)}$ : 각각 voice/unvoiced segment의 impulse response로써, $t$에 해당하는 $k$-th frame의 BAP에 inverse Fourier transform을 적용하여 계산됨
    - $*$ : convolution operation
    - 논문에서는 $g_{p}=0.1, g_{n}=0.003$으로 설정

FIRNet으로 생성된 Signal

• Causal Convolution Block
  • 논문에서는 정확한 latent representation을 얻기 위해 ConvNeXt v2 architecture를 core module로 활용함
    - 구조적으로, depthwise convolution layer, layer normalization, GELU activation을 사용한 point-wise convolution, global response normalization, output pointwise convolution으로 구성됨
  • 이때 input depthwise convolution layer에 causality를 추가하고 kernel size를 5로 설정함
    - Causal convolution block에는 2개의 ConvNeXt core block이 포함됨
    - 한편으로 BAP, MGC, residual FIR network의 output channel은 각각 128, 256, 128로 설정

• FIR Network
  • FIR network는 multiple FIR filter를 사용하여 input signal을 output signal로 변환함
  • 여기서 $h^{(1,k)},h^{(2,k)},...,h^{(M,k)}$는 해당 FIR filter의 impulse response coefficient, $x^{(0)}(t), x^{(M)}(t)$는 각각 input/output signal, $x^{(1)}(t),x^{(2)}(t),...,x^{(M-1)}(t)$는 다음과 같이 정의되는 intermediate output signal을 나타냄:
    (Eq. 2) $x^{(m)}(t)=h^{(m,k)}*x^{(m-1)}(t)+x^{(m-1)}(t)$
    
  • 최종적으로 dilated causal convolution layer를 사용하여 auxiliary feature의 latent representation과 previous impulse response coefficient로부터 $m$-th FIR filter의 impulse response coefficient를 추정함
    - 이때 latent channel 수를 128, dilated causal convolution의 kernel size를 3, 나머지는 1로 설정함
    - Residual, resonance FIR network에는 tap size가 256인 8개의 FIR filter가 포함됨
    - 8개의 dilated causal convolution layer의 dilation size는 $[1,2,4,8,1,2,4,8]$

- Training Criteria

• FIRNet은 generative adversarial network로써,
  • Generator의 objective로 다음의 4가지 loss를 사용:
    - Least squares를 사용한 adversarial loss $\mathcal{L}_{adv}$
    - Feature matching loss $\mathcal{L}_{fm}$
    - Speech waveform에 대한 mel-spectral $L1$ loss $\mathcal{L}_{mel}$
    - Residual signal에 대한 source excitation regularization loss $\mathcal{L}_{reg}$
  • 결과적으로 objective function $\mathcal{L}_{G}$는:
    (Eq. 3) $\mathcal{L}_{G} = \mathcal{L}_{adv}+\lambda_{fm}\mathcal{L}_{fm}+\lambda_{mel}\mathcal{L}_{mel}+\lambda_{reg}\mathcal{L}_{reg}$
    - $\lambda_{fm},\lambda_{mel},\lambda_{reg}$ : 각 loss에 대한 hyperparameter
    - 논문에서는 $\lambda_{fm}=2.0, \lambda_{mel}=50.0, \lambda_{reg} =20.0$으로 설정

3. Experiments

- Settings

• Dataset : Hi-Fi-CAPTAIN corpus
• Comparisons : WORLD, SiFi-GAN

- Results

• Effectiveness of FIR filters
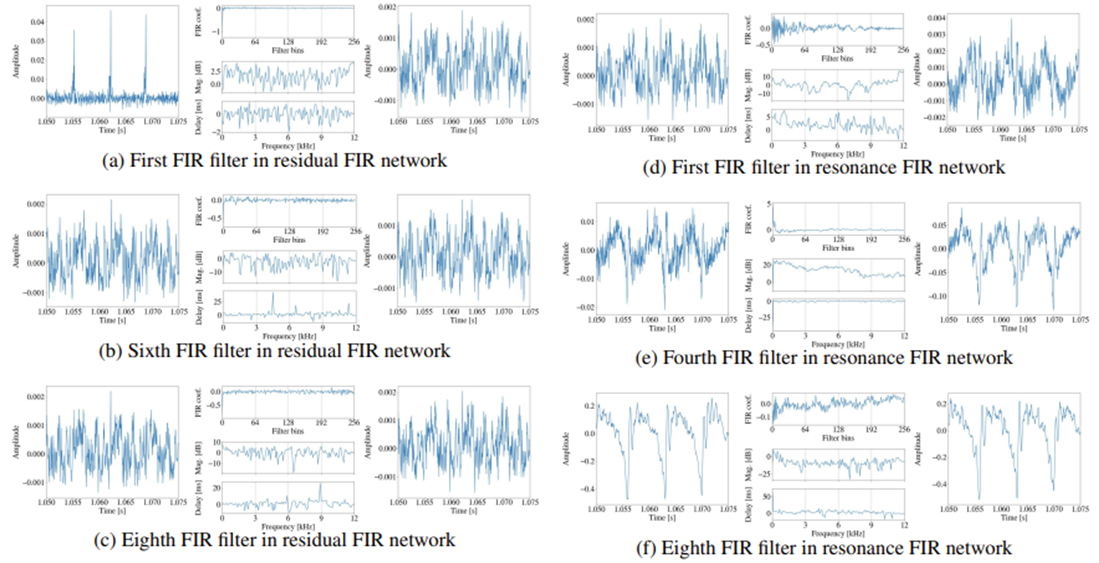
  • 아래 그림과 같이 다양한 FIR filter의 impulse response와 해당 input, output signal을 확인해 보면
  • (a)의 first FIR filter는 source excitation signal의 waveform shape를 크게 변화시킴
    - 그 외의 나머지 FIR filter는 input signal의 waveform shape에 조금만 영향을 줌
    - 이는 residual FIR network에서 FIR filter 수를 줄일 수 있다는 것을 의미함
  • 한편으로 resonance FIR network에서는 filtered waveform shape가 successive FIR filter와 convolution 되면서 점진적으로 변화하는 것으로 나타남
    - 특히 resonance FIR network의 impulse response는 residual FIR network의 impulse response와 다른 shpae를 가짐
    - 즉, fine spectral envelope를 얻기 위해서는 많은 FIR filter나 long tap size를 사용하여 impulse response를 길게 만들어야 함

FIR filter의 Impulse Response

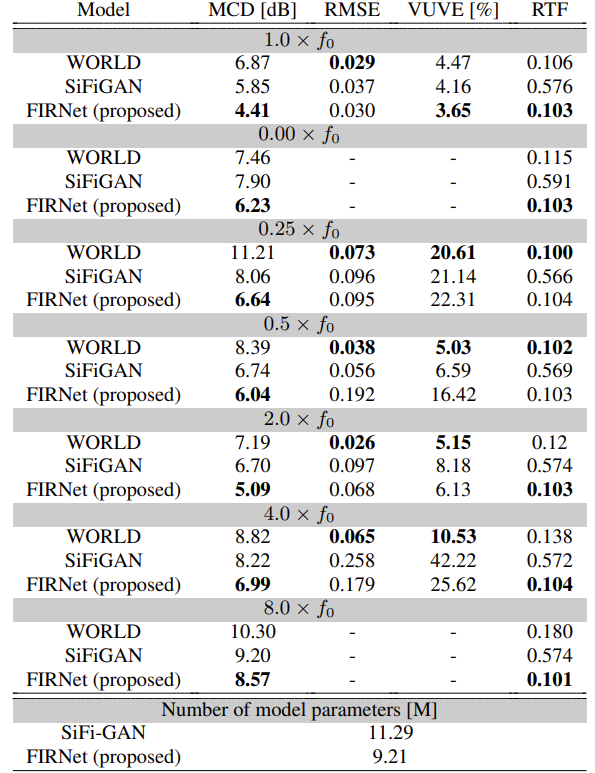
• Objective Evaluation
  • FIRNet은 모든 $f_{0}$ condition에서 가장 낮은 MCD를 달성함
  • 생성 속도 측면에서 FIRNet은 SiFi-GAN 보다 5배 빠르고, $f_{0}$ scaling condition이 큰 경우 WORLD 보다 빠름

모델 성능 비교

• Subjective Evaluation
  • MOS 측면에서도 FIRNet은 다양한 $f_{0}$에 대해 뛰어난 합성 품질과 robustness를 달성함

$f_{0}$별 MOS 비교