[Paper 리뷰] WaveFit: An Iterative and Non-autoregressive Neural Vocoder based on Fixed-Point Iteration

WaveFit: An Iterative and Non-autoregressive Neural Vocoder based on Fixed-Point Iteration

---

• Denoising Diffusion Probabilistic Model (DDPM)과 Generative Adversarial Network (GAN)은 neural vocoder에서 자주 활용되고 있음
• WaveFit
  • Fixed-point iteration을 기반으로 하는 DDPM-like iterative framework에 GAN의 특성을 통합
  • Input signal을 iteratively denoise 하고 모든 iteration에서 intermediate output의 adversarial loss를 최소화
• 논문 (SLT 2023) : Paper Link

---

1. Introduction

• Neural vocoder는 acoustic feature가 주어지면 speech waveform을 생성하는 것을 목표로 함
  • Autoregressive (AR) 모델의 경우 많은 양의 sequential operation이 필요하므로 느린 추론 속도를 가진다는 단점이 있음
  • 따라서 추론 속도 향상을 위해 non-AR 모델이 주로 활용됨
    - Normalizing flow, Generative Adversarial Network (GAN), Denoising Diffusion Probabilistic Model (DDPM) 등
    - 특히 DDPM-based vocoder는 가장 우수한 합성 품질을 얻을 수 있지만, waveform을 얻기 위해서 여러 번의 iterative refine이 필요함
  • Iteration을 줄이기 위해 DDPM과 GAN의 essence가 coexist 한다는 점을 활용할 수 있음
    - 특히 Denoising diffusion GAN은 generator를 사용하여 diffuse 된 sample에서 clean sample을 예측하고, discriminator를 통해 이를 구별하는 방식으로 동작함
    - 해당 전략은 input text가 주어지고 log mel-spectrogram을 예측하는 text-to-speech 작업에도 적용되고 있음

-> 그래서 적은 iteration 만으로도 고품질의 합성을 달성하기 위해 DDPM과 GAN을 결합한 WaveFit을 제안

 

• WaveFit
  • GAN-based loss를 사용하여 학습된 iterative-style non-AR neural vocoder
  • Fixed-point iteration을 활용하여 output이 target speech에 가까워지도록 input signal을 denoising 하는 denoising mapping을 iterative 하게 적용
  • GAN-based loss와 STFT loss를 결합한 loss function을 도입하고 모든 iteration에 대해 loss를 적용함으로써 intermediate output이 target speech와 가까워지도록 함

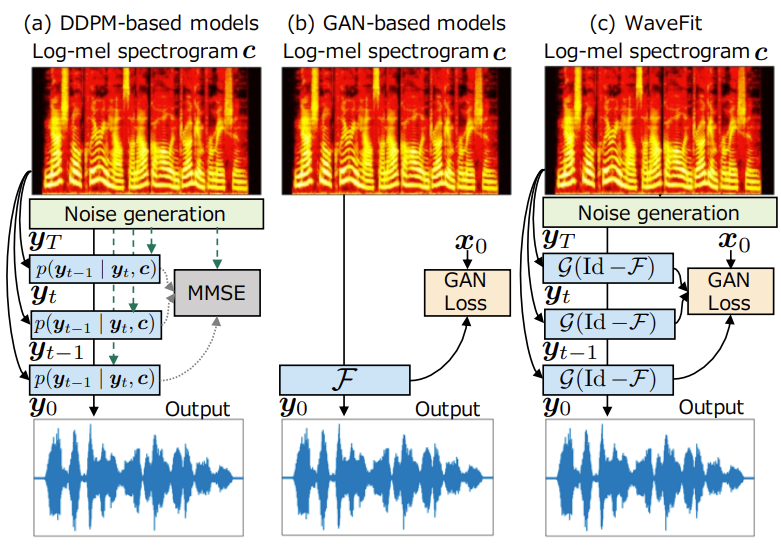
< Overall of WaveFit >

• Fixed-point iteration을 기반으로 하는 DDPM-like iterative framework에 GAN의 특성을 통합
• Input signal을 iteratively denoise 하고 모든 iteration에서 intermediate output의 adversarial loss를 최소화
• 결과적으로 기존 DDPM-based vocoder 더 적은 iteration 만으로도 우수한 합성 품질을 달성

Overview of (a) DDPM Vocoder (b) GAN Vocoder (c) WaveFit

2. Non-autoregressive Neural Vocoders

• Neural vocoder는 log mel-spectrogram $c = (c_{1},...,c_{K})\in \mathbb{R}^{FK}$가 주어지면 speech waveform $y_{0} \in \mathbb{R}^{D}$를 생성함
  • $c_{K} \in \mathbb{R}^{F}$ : $k$-th time frame의 $F$-point log mel-spectrum, $K$ : time frame 수
  • 적은 계산으로 target speech $x_{0} \in \mathbb{R}^{D}$와 indistinguishable 한 $y_{0}$를 생성하는 neural vocoder를 구성하는 것이 목표

- DDPM-based Neural Vocoder

• DDPM-based neural vocoder는 $x_{0}$의 latent variable model로써,
  • $q(x_{0}|c)$는 $q(x_{T}) = \mathcal{N}(0,I)$에서 시작하는 learned Gaussian transition을 갖춘 $x_{t} \in \mathbb{R}^{D}$의 $T$-step Markov chain을 기반으로 하고, 다음과 같이 정의됨:
    (Eq. 1) $q(x_{0}|c)=\int_{\mathbb{R}^{DT}}q(x_{T})\prod_{t=1}^{T}q(x_{t-1}|x_{t},c)\mathrm{d}x_{1}...\mathrm{d}x_{T}$
    - $q(x_{t-1}|x_{t},c)$, $y_{0}\sim q(x_{0}|c)$를 모델링하는 것은 $q(y_{t-1}|y_{t},c)$에서 $y_{t-1}$을 recursive sampling 하는 것으로 볼 수 있음
  • DDPM-based neural vocoder는 $p(x_{t}|x_{t-1}) = \mathcal{N}(\sqrt{1-\beta_{t}}x_{t-1},\beta_{t}I)$로 주어진 noise schedule $\{\beta_{1},...,\beta_{T}\}$에 따라 waveform에 Gaussian noise를 점진적으로 더하는 diffusion process를 통해 $x_{t}$를 생성함
    - 이를 통해 $x_{t}=\sqrt{\bar{\alpha}_{t}}x_{0}+\sqrt{1-\bar{\alpha}_{t}}\epsilon$와 같은 closed form으로 arbitrary timestep $t$에서 $x_{t}$를 sampling 할 수 있음
    - $\alpha_{t}=1-\beta_{t}, \bar{\alpha}_{t}=\prod_{s=1}^{t}\alpha_{s}, \epsilon \sim \mathcal{N}(0,I)$
    
  • 이때 DDPM-based vocoder는 $x_{t}$로부터 $\epsilon$을 $\hat{\epsilon} = \mathcal{F}_{\theta}(x_{t},c,\beta_{t})$로 예측하기 위해, parameter $\theta$를 가지는 DNN $\mathcal{F}$를 사용
    1. 일반적으로 DNN $\mathcal{F}$는 Evidence Lower BOund (ELBO)를 최대화하는 방식으로 학습될 수 있지만, DDPM-based vocoder는 주로 iteration $t$에 해당하는 loss weight를 omit 한 simplified loss를 사용:
       (Eq. 2) $\mathcal{L}^{WG}=||\epsilon-\mathcal{F}_{\theta}(x_{t},c,\beta_{t})||_{2}^{2}$
       - $|| \cdot ||_{p}$ : $\ell_{p}$ norm
       
    2. $\beta_{t}$가 충분히 작다면 $q(x_{t-1}|x_{t},c)$는 $\mathcal{N}(\mu_{t},\gamma_{t}I)$로 주어질 수 있고, $q(y_{t-1}|y_{t},c)$로부터의 recursive sampling은 아래의 식을 $t=T,...,1$를 따라 iterating 함으로써 얻어짐:
       (Eq. 3) $y_{t-1} = \frac{1}{\sqrt{\alpha_{t}}}\left( y_{t}-\frac{\beta_{t}}{\sqrt{1-\bar{\alpha}_{t}}}\mathcal{F}_{\theta}(y_{t},c,\beta_{t}) \right)+\gamma_{t}\epsilon$
       - $\gamma_{t}=\frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_{t}}\beta_{t}, y_{T}\sim\mathcal{N}(0,I), \gamma_{1}=0$
  • 이때 DDPM-based neural vocoder는 만족스러운 품질을 위해 200회 이상의 iteration이 필요하므로, 품질을 유지하면서 iteration 수를 줄이기 위해 noise prior 분포를 활용할 수 있음
• Prior Adaptation from Conditioning log Mel-spectrogram
  • Iteration 수를 줄이기 위해 PriorGrad와 SpecGrad는 $c$로부터 계산되는 $\Sigma$를 활용한 adaptive prior $\mathcal{N}(0,\Sigma)$를 도입
    1. 특히 SpecGrad는 $\Sigma$가 positive semi-definite이고 $\Sigma = LL^{\top}$으로 decompose 된다는 점을 활용
       - $L \in \mathbb{R}^{D\times D}$, $^{\top}$ : transpose
    2. 그러면 $\mathcal{N}(0,\Sigma)$에서 sampling은 $\tilde{e} \sim \mathcal{N}(0,I)$를 사용하여 $e = L\tilde{e}$로 나타낼 수 있고, (Eq. 2)에 adaptive prior를 적용하면:
       (Eq. 4) $\mathcal{L}^{SG}=||L^{-1}(\epsilon-\mathcal{F}_{\theta}(x_{t},c,\beta_{t}))||_{2}^{2}$
       
  • 이때 SpecGrad는 $L=G^{+}MG$를 정의하고 $L^{-1} \approx G^{+}M^{-1}G$를 근사함
    - $NK \times D$의 matrix $G$는 STFT를 나타내고, $G^{+}$는 dual window를 사용한 inverse STFT (iSTFT)의 matrix representation
    - $M = \mathrm{diag}[(m_{1,1},...,m_{N,K})]\in\mathbb{C}^{NK\times NK}$는 각 $(n,k)$-th time-frequency (T-F) bin에 대한 filter coefficient를 나타내는 diagonal matrix
    
  • 따라서 $L, L^{-1}$은 각각 T-F domain에서 time-varying filter와 근사 inverse filter로 구현될 수 있음
    - 여기서 T-F domain filter $M$은 minimum phase response로, $c$를 통해 계산된 spectral envelop에 의해 얻어짐
    - Spectral envelope는 $c$에서 계산된 power spectrogram에 24-th order lifter를 적용하여 얻을 수 있음
• InferGrad
  • 기존의 DDPM-based vocoder는 DNN이 (Eq. 2)와 같은 simplified loss를 사용하여 Gaussian denoiser로 학습되므로 생성된 음성이 target과 가까워진다는 보장이 없음
  • InferGrad는 모든 training step에서 (Eq. 3)을 통해 random signal $\epsilon$으로부터 $y_{0}$를 합성한 다음, $y_{0}$와 target $x_{0}$ 간의 차이를 나타내는 infer loss $\mathcal{L}^{IF}$를 도입함
  • 이때 InferGrad의 loss function은:
    (Eq. 5) $\mathcal{L}^{IG} = \mathcal{L}^{WG}+\lambda_{IF}\mathcal{L}^{IF}$
    - $\lambda_{IF} >0$ : tunable weigth parameter

- GAN-based Neural Vocoder

• Non-AR neural vocoder로써 adversarial training을 활용할 수도 있음
  • 이때 generator는 discriminator가 distinguish 하기 어려운 waveform을 생성하고, discriminator는 target과 생성된 waveform을 discriminate 하도록 학습됨
    - GAN-based vocoder에서 non-AR DNN $\mathcal{F} : \mathbb{R}^{FK} \rightarrow \mathbb{R}^{D}$는 $y_{0}=\mathcal{F}_{\theta}(c)$를 통해 $c$에서 $y_{0}$를 directly output 함
  • GAN-based vocoder는 주로 multiple resolution에 대한 multiple discriminator를 활용함
    1. 대표적으로 MelGAN은 multi-scale discriminator (MSD)를 도입하고, target과 생성된 음성의 discriminator feature map 간의 mean absolute error (MAE)를 최소화하는 feature matching loss를 도입
    2. 여기서 GAN-based vocoder의 generator와 discriminator에 대한 loss $\mathcal{L}_{Gen}^{GAN}, \mathcal{L}_{Dis}^{GAN}$는:
       (Eq. 6) $\mathcal{L}_{Gen}^{GAN}=\frac{1}{R_{GAN}}\sum_{r=1}^{R_{GAN}}-\mathcal{D}_{r}(y_{0})+\lambda_{FM}\mathcal{L}_{r}^{FM}(x_{0},y_{0})$
       (Eq. 7) $\mathcal{L}_{Dis}^{GAN}=\frac{1}{R_{GAN}}\sum_{r=1}^{R_{GAN}}\max(0,1-\mathcal{D}_{r}(x_{0}))+\max(0,1+\mathcal{D}_{r}(y_{0}))$
       - $R_{GAN}$ : discriminator 수, $\lambda_{FM} \geq 0$ : $\mathcal{L}^{FM}$에 대한 tunable weight
    3. $r$-th discriminator $\mathcal{D}_{r} : \mathbb{R}^{D}\rightarrow \mathbb{R}$은 $\mathcal{D}_{r}=\mathcal{D}^{H}_{r} \circ ... \circ \mathcal{D}^{1}_{r}$과 같이 $H$개의 sub-layer로 구성됨
       - $\mathcal{D}^{h}_{r} : \mathbb{R}^{D_{h-1,r}}\rightarrow \mathbb{R}^{D_{h,r}}$
    4. 그러면 $r$-th discriminator의 feature matching loss는:
       (Eq. 8) $\mathcal{L}_{r}^{FM}(x_{0},y_{0})=\frac{1}{H-1}\sum_{h=1}^{H-1}\frac{1}{D_{h,r}}||d_{x,0}^{h}-d_{y,0}^{h}||_{1}$
       - $d_{a,b}^{h}$ : $\mathcal{D}_{r}^{h-1}(a_{b})$의 output
  • Auxiliary loss로써 multi-resolution STFT loss는 adversarial training을 안정화하기 위해 사용됨
    1. Multi-resolution STFT loss $\mathcal{L}^{MR \text{-} STFT}$는 spectral convergence loss와 magnitude loss로 구성됨:
       (Eq. 9) $\mathcal{L}^{MR \text{-}STFT}(x_{0},y_{0})=\frac{1}{R_{STFT}}\sum_{r=1}^{R_{STFT}}\mathcal{L}_{r}^{Sc}(x_{0},y_{0})+\mathcal{L}_{r}^{Mag}(x_{0},y_{0})$
       -$R_{STFT}$ : STFT configuration 수
    2. $\mathcal{L}_{r}^{Sc}, \mathcal{L}_{r}^{Mag}$는 각각 $r$-th STFT configuration의 spectral loss, magnitude loss에 해당함
       - $\mathcal{L}^{Sc}_{r}(x_{0},y_{0})= \frac{||X_{0,r}-Y_{0,r}||_{2}}{||X_{0,r}||_{2}}$
       - $\mathcal{L}^{Mag}_{r}(x_{0},y_{0})= \frac{1}{N_{r}K_{r}}|| \ln (X_{0,r})-\ln(Y_{0,r})||_{1}$
       - $N_{r},K_{r}$ : 각각 $r$-th STFT configuration의 frequency bin, time-frame 수
       - $X_{0,r} \in \mathbb{R}^{N_{r}K_{r}}, Y_{0,r} \in \mathbb{R}^{N_{r},K_{r}}$ : 각각 $x_{0}, y_{0}$의 $r$-th STFT configuration을 가지는 amplitude spectrogram
  • 최근 GAN의 essence가 DDPM에 통합될 수 있음이 제시되었기 때문에, 이러한 결합을 통해 vocoder 작업에서도 적은 iteration 횟수로 고품질 합성을 달성할 수 있음

3. Fixed-Point Iteration

• Fixed-point theory를 DNN과 결합하여 data-driven iterative algorithm을 설계할 수 있음
  • Mapping $\mathcal{T}$의 fixed-point는 $\mathcal{T}$에 의해 변하지 않는 point $\phi$를 의미 (i.e., $\mathcal{T}(\phi) = \phi$)
    1. 이때 $\mathcal{T}$의 모든 fixed point들의 set은:
       (Eq. 10) $\mathrm{Fix}(\mathcal{T})=\{ \phi \in \mathbb{R}^{D}| \mathcal{T}(\phi)=\phi\}$
    2. Mapping $\mathcal{T}$가 firmly quasi-nonexpansive 하다면:
       (Eq. 11) $|| \mathcal{T}(\xi)-\phi ||_{2}\leq || \xi-\phi||_{2}$
       - 모든 $\xi \in \mathbb{R}^{D}$와 $\phi \in \mathrm{Fix}(\mathcal{T}) (\neq \varnothing)$에 대해 $\mathcal{T} = \frac{1}{2}\mathrm{Id}+\frac{1}{2} \mathcal{F}$를 충족하는 quasi-mapping $\mathcal{F}$가 존재함
       - $\mathrm{Id}$ : identity operator
    3. 그러면 모든 inital point에 대해 다음의 fixed-point iteration은 fixed point $\mathcal{T}$로 수렴함:
       (Eq. 12) $\xi_{n+1} = \mathcal{T}(\xi_{n})$
       - 즉, initial point $\xi_{0}$에서 (Eq. 12)를 iterating 함으로써 $\xi_{0}$의 choice에 따라 fixed point $\mathcal{T}$를 찾을 수 있음
  • Fixed-point iteration은
    1. Iterative refinement를 generalization 한 proximal point algorithm으로 볼 수 있음:
       (Eq. 13) $\xi_{n+1} = \mathrm{prox}_{\mathcal{L}}(\xi_{n})$
    2. 이때 $\mathrm{prox}_{\mathcal{L}}$은 loss function $\mathcal{L}$의 proximity operator로써:
       (Eq. 14) $\mathrm{prox}_{\mathcal{L}}(\xi)\in \arg \min_{\zeta}\left[\mathcal{L}(\zeta)+\frac{1}{2}|| \xi -\zeta||_{2}^{2}\right]$
       - $\mathcal{L}$이 적절한 lower-semicontinuous convex이면, $\mathrm{prox}_{\mathcal{L}}$은 firmly (quasi-) nonexpansive이므로 proximal point algorithm으로 생성된 sequence는 $\mathrm{Fix}(\mathrm{prox}_{\mathcal{L}}) = \arg\min_{\zeta}\mathcal{L}(\zeta)$의 point로 수렴함
       - 즉, (Eq. 13)은 loss function $\mathcal{L}$을 최소화함
    3. (Eq. 14)는 $\exp (-\mathcal{L}(\cdot))$에 prior proportional 하는 Gaussian observation model을 기반으로 한 maximum a posteriori estimation의 negative log-likelihood로 볼 수 있음
       - 이때 (Eq. 13)은 DDPM-based method와 동일한 iterative Gaussian denoising algorithm이므로, fixed-point theory를 적용할 수 있음
  • Firmly quasi-nonexpansive mapping의 중요한 property는 attracting 하다는 것
    1. 즉, (Eq. 11)의 equality가 발생하지 않음 : $|| \mathcal{T}(\xi)-\phi||_{2}< || \xi-\phi||_{2}$
       - 결과적으로 $\mathcal{T}$를 사용하면 항상 input signal $\xi$가 fixed point $\phi$에 더 가깝게 이동할 수 있음
    2. 여기서 denoising mapping을 input signal에서 noise를 제거하는 $\mathcal{T}$로 고려해 보면,
       - 이 경우 (Eq. 12)의 fixed-point iteration은 iterative denoising algorithm이고 attracting property는 각 iteration이 항상 signal을 refine 하도록 보장함
       - Denoising mapping의 fixed point $\mathcal{T}(\phi)=\phi$는 더 이상 denoising을 수행할 수 없는 clean signal $\phi$가 될 때까지 수렴됨
    3. 따라서 speech signal에 specialize 된 denoising mapping이 존재한다면, 임의의 signal에서 (Eq. 12)를 iterating 함으로써 clean speech signal을 얻을 수 있음

4. Proposed Method

• WaveFit은 fixed-point theory를 음성 생성 작업에 적용함
  • 이를 위해 (Eq. 11)을 만족하는 denoising mapping으로 DNN을 구성함
  • 추가적으로 해당 property를 approximately impose 하는 loss function을 도입

- Model Overview

• WaveFit은 $y_{t-1}$이 $x_{0}$에 가까워지도록 $y_{t}$를 refine 하기 위해 denoising mapping을 iterative 하게 적용함
  • 결과적으로 아래 식을 $T$번 iterating 함으로써 speech signal $y_{0}$를 생성함:
    (Eq. 15) $y_{t-1}=\mathcal{G}(z_{t},c), \,\,\, z_{t}=y_{t}-\mathcal{F}_{\theta}(y_{t},c,t) $
    - $\mathcal{F}_{\theta} : \mathbb{R}^{D}\rightarrow \mathbb{R}^{D}$는 noise component $y_{T} \sim \mathcal{N}(0,\Sigma)$를 추정하는 DNN이고, 이때 $\Sigma$는  SpecGrad의 initializer에 의해 주어짐
    - $\mathcal{G}(z,c) : \mathbb{R}^{D} \rightarrow \mathbb{R}^{D}$는 $z_{t}$의 signal power를 $c$로 정의된 target signal의 power로 조정하는 gain adjustment operator
  • 여기서 target power $P_{c}$는 $c$로부터 계산된 power spectrogram을 통해 계산됨
    - 이후 $z_{t}$의 power는 $P_{z}$로써 계산되고, $z_{t}$의 gain은 $y_{t} = (P_{c}/(P_{z}+s))z_{t}$로 adjust 됨
    - $s=10^{-8}$ : zero-division을 방지하기 위한 scalar
    

- Loss Function

• WaveFit은 mapping $\mathcal{G}(\mathrm{Id}-\mathcal{F}_{\theta})$이 firmly quasi-nonexpansive mapping인 경우, fixed-point iteration을 통해 random noise $y_{T}$로부터 clean speech를 얻을 수 있음
  • 일반적으로 DNN-based function이 firmly quasi-nonexpansive mapping임을 보장하기는 어렵지만, 이러한 property를 approximately impose 할 수 있는 loss function을 설계
    - Firmly quasi-nonexpansive mapping의 가장 중요한 property는 output signal $y_{t-1}$이 항상 input signal $y_{t}$보다 $x_{0}$에 더 가깝다는 것
  • 따라서 denoising mapping에 해당 property를 적용하기 위해, 모든 intermediate output $y_{0}, y_{1},...,y_{T-1}$에 대한 loss value를 combine 함:
    (Eq. 16) $\mathcal{L}^{WaveFit}=\frac{1}{T}\sum_{t=0}^{T-1}\mathcal{L}^{WF}(x_{0},y_{t})$
    
  • 이때 loss function $\mathcal{L}^{WF}$는 아래의 2가지 demand를 기반으로 설계됨
    
    1. Output waveform은 high-fidelity signal이어야 함
    2. Loss function은 imperceptible phase difference에 insensitive 해야 함
       - Conditioning log mel-spectrogram에 해당하는 DNN의 fixed-point에는 여러 waveform이 포함될 수 있기 때문
       - 이때 initial phase difference로 인해 conditioning log mel-spectrogram에 해당하는 waveform의 수가 적을 수 있으므로 squared-error와 같은 phase-sensitive loss는 $\mathcal{L}^{WF}$로 적합하지 않음
  • 결과적으로 WaveFit은 imperceptible phase difference에 insensitive 한 GAN-based loss와 multi-resolution STFT loss를 결합하여 loss로 사용:
    (Eq. 17) $\mathcal{L}^{WF}(x_{0},y_{t})=\mathcal{L}^{GAN}_{Gen}(x_{0},y_{t})+\lambda_{STFT}\mathcal{L}^{STFT}(x_{0},y_{t})$
    - $\lambda_{STFT} \geq 0$ : tunable weight
    1. GAN-based loss $\mathcal{L}^{GAN}_{Gen}$은 multi-resolution discriminator와 feature-matching loss를 결합하여 사용함
       - 이때 hinge loss를 사용하기 위해 (Eq. 6)을 아래와 같이 수정하면:
       (Eq. 18) $\mathcal{L}_{Gen}^{GAN}(x_{0},y_{t})=\sum_{r=1}^{R} \max(0,1-\mathcal{D}_{r}(y_{t}))+\lambda_{FM}\mathcal{L}_{r}^{FM}(x_{0},y_{t})$
       - Discriminator loss의 경우 (Eq. 7)의 $\mathcal{L}_{Dis}^{GAN}(x_{0},y_{t})$를 계산한 다음, 모든 intermediate output $y_{0},...,y_{T-1}$에 대해 평균됨
    2. $\mathcal{L}^{STFT}$의 경우, adversarial training을 안정화하기 위해 $\mathcal{L}^{MR\text{-}STFT}$를 사용함
       - 이때 HiFi-GAN과 같이 target과 생성된 음성 간의 amplitude mel-spectrogram의 MAE loss를 적용하면:
       (Eq. 19) $\mathcal{L}^{STFT}(x_{0},y_{t})=\mathcal{L}^{MR\text{-}STFT}(x_{0},y_{t})+\frac{1}{FK}||X_{0}^{Mel}-Y_{t}^{Mel}||_{1}$
       - $X^{Mel}_{0} \in \mathbb{R}^{FK}, Y_{t}^{Mel} \in \mathbb{R}^{FK}$ : 각각 $x_{0}, y_{t}$의 amplitude mel-spectrogram

- Differences Between WaveFit and DDPM-based Vocoders

• 기존 vocoder와 WaveFit 간의 차이점을 비교해 보면
  • DDPM-based vocoder는 probability theory를 활용하는 반면, WaveFit은 fixed-point theory를 사용함
    - Fixed-point theory는 optimization과 adaptive filter algorithm의 deterministic analysis를 지원하기 때문에, WaveFit은 optimization-based/adaptive-based neural vocoder로 볼 수 있음
  • 논문에서 WaveFit을 제안하는 이유는 다음과 같음:
    1. 각 iteration 마다 random noise를 추가하면 DDPM-based vocoder가 proceed 되는 direction이 distrub 됨
       - Intermediate signal은 phase를 randomly change 하기 때문에, phase distortion으로 인해 high frequency range에서 artifact가 발생함
       
    2. Noise addition이 없는 DDPM-based vocoder는 sine-wave-like artifact 같은 notable artifact를 생성함
       - 이는 DDPM-based vocoder의 trained mapping이 randomness에만 초점을 맞추고, input signal을 target signal 쪽으로 이동시키지 않는다는 것을 의미함
       -> 결과적으로 기존의 DDPM-based vocoder는 iteration 수를 줄이는데 근본적인 한계가 있음
  • 이와 달리 WaveFit은 random noise를 추가하지 않으면서 intermediate signal을 denoising 함
    - 특히 (Eq. 16)은 각 iteration에서 target speech로의 denoising direction을 가짐
    - 따라서 WaveFit은 iterative denoising을 통해 음성 품질을 유지하면서 iteration 수를 효과적으로 줄일 수 있음
  • 한편으로 WaveFit의 1회 iteration에 대한 계산 비용은 DDPM-based vocoder의 계산 비용과 거의 동일하지만, 전체 WaveFit을 학습시키기 위해서는 더 많은 계산 비용이 필요함
    - 이는 (Eq. 16)의 loss function이 모든 intermediate output에 대한 GAN-based loss function으로 구성되기 때문
    - 추가적으로 WaveFit은 이러한 GAN-based loss를 $T$번 계산한다는 점도 영향을 줌

- Implementation

• Network Architecture
  • 13.8M의 trainable parameter를 가지는 WaveGrad를 $\mathcal{F}$의 base model로써 사용함
    - Initial noise $y_{T}\sim \mathcal{N}(0, \Sigma)$를 계산하기 위해 SpecGrad의 noise generation algorithm을 활용
  • 각 discriminator $\mathcal{D}_{r}$은 MelGAN과 동일한 architecture를 사용
    - $R_{GAN}=3$이고, structurally identical discriminator가 서로 다른 resolution (original, $2\times$ downsampling, $4\times$ downsampling)의 input audio에 적용됨
    - $\mathcal{D}_{r}$의 output logit 수는 input length에 proportional함
  • 따라서 (Eq. 6), (Eq. 7)의 평균을 각각 generator와 discriminator의 loss function으로 사용함
• Hyperparameters
  • 모든 input signal은 24kHz로 up/down sampling 되고, $c$의 경우 $F=128$-dimensional log mel-spectrogram을 사용
    - 여기서 triangular mel-filterbank의 lower/upper frequency bound는 각각 20Hz, 12kHz
    - Mel-spectrogram 계산과 initial noise 생성을 위해 50ms Hann window, 12.5ms frame shift, 2048-point FFT를 가지는 STFT configuration을 사용
  • $\mathcal{L}^{MR\text{-}STFT}$의 경우, $R_{STFT}=3$ resolution을 활용
    - 각 resolution의 Hann window, frame shift, FFT point는 각각 $[360,900,1800], [80,150,300], [512,1024,2048]$
    - Amplitude mel-spectrogram의 MAE loss에 대해 위 STFT configuration을 사용하여 128-dimensional mel-spectrogram을 추출

5. Experiments

- Settings

• Dataset : LibriTTS
• Comparisons : InferGrad, SpecGrad, Multi-Band MelGAN, HiFi-GAN, WaveRNN

- Results

• Verification Experiments for Intermediate Outputs
  • WaveFit의 intermediate output이 target speech에 approaching 하는지를 확인해 보면
  • 각 iteration에서 WaveFit에 대한 metric들이 모두 decay 하고, 3번의 iteration만으로도 거의 수렴하는 것으로 나타남

Intermediate Output에 대한 Iteration 별 수렴 비교

• Comparison with WaveRNN and DDPM-based Models
  • MOS, RTF 측면에서 성능을 비교해 보면
  • 제안된  WaveFit이 가장 우수한 합성 품질과 RTF를 보임

DDPM-based Vocoder, WaveRNN과의 비교

• 마찬가지로 side-by-side test에서도 WaveFit이 가장 선호되는 것으로 나타남

Side-by-Side test 결과

• Comparison with GAN-based Models
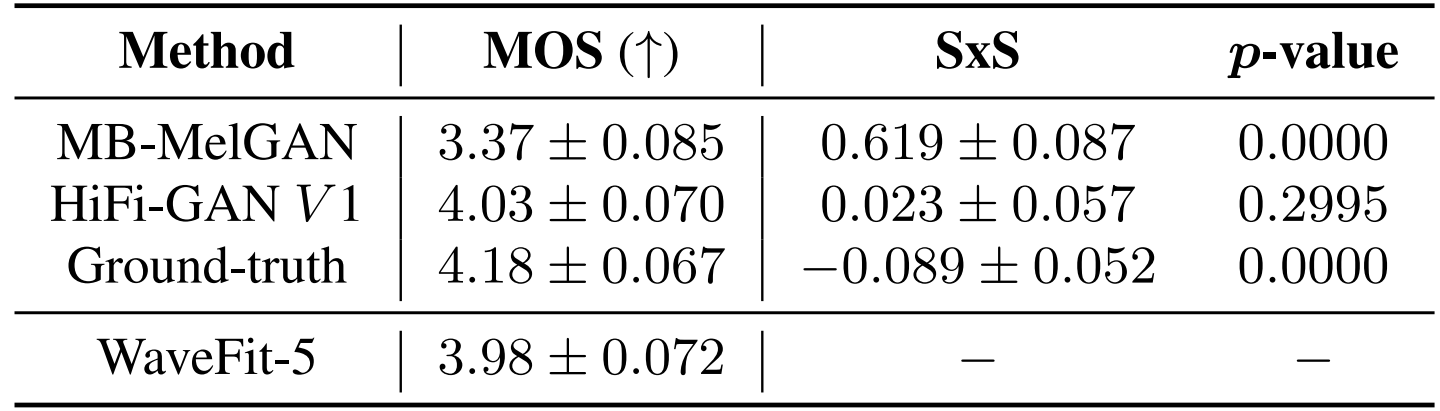
  • MOS 측면에서 비교해 보면
  • WaveFit은 MB-MelGAN 보다는 우수한 성능을 보이고 HiFi-GAN과 비슷한 수준의 합성 품질을 달성함

GAN-based Vocoder와의 비교