[Paper 리뷰] InferGrad: Improving Diffusion Models for Vocoder by Considering Inference in Training

InferGrad: Improving Diffusion Models for Vocoder by Considering Inference in Training

---

• Denoising diffusion probabilistic model은 추론 과정에서 많은 반복이 필요하므로 추론 속도가 느림
• 추론 속도 향상을 위해 추론 schedule을 최적화하는 것이 필요
  - However, 일반적으로 추론과 학습 process는 개별적으로 최적화됨
• InferGrad
  • 추론 process를 학습에 통합한 vocoder용 diffusion model
  • 학습 중 추론 schedule에 따라 reverse process를 통해 random noise로부터 data를 생성하여, 생성된 data와 실제의 차이를 최소화
• 논문 (ICASSP 2022) : Paper Link

---

1. Introduction

• 음성 합성에서 autoregressive model, normalizing flow, variational autoencoder, generative adversarial network 등의 다양한 방법론들이 시도됨
  • 최근에는 Denoising Diffusion Probabilistic Model (DDPM)이 우수한 성능을 보이고 있음 
    1. Data 분포를 Gaussian noise와 같은 known prior noise 분포로 변환하는 diffusion-forward process
    2. Learned score function을 활용하여 random noise로부터 data sample을 점진적으로 복구하는 denoising-reverse process
  • Diffusion model은 reverse process의 step 수가 forward process의 step 수와 일치하면, 학습된 gradient information을 완전히 활용할 수 있고, 생성 품질을 극대화할 수 있음
    -> BUT, reverse process의 step 수가 많아질수록 diffusion model의 추론 속도가 저하됨
• 결과적으로 앞선 연구들은 품질 저하를 감안하고 reverse step을 줄여 생성 속도를 가속화하는 방식을 사용함
  • 일반적으로 학습 과정을 변경하지 않고 추론 noise schedule에 대한 선택만을 최적화함
    - WaveGrad는 최적의 추론 schedule을 찾기 위해 grid search를 활용
    - BDDM은 추론 schedule을 최적화하는 extra scheduling network를 활용
    - DDIM은 non-Markovian process로 reparameterize하여 추론 shcedule을 지원
  • 위의 방법들은 학습 과정에서의 noise schedule과 추론 과정에서의 noise schedule이 분리되어 있기 때문에 추론 schedule에 대한 생성 품질을 향상하기 어려움
    -> 따라서 추론 schedule을 학습에 통합하고, 그에 따라 DDPM을 최적화하는 방법이 필요함

-> 그래서 inference/reverse process를 학습 과정에 통합시킨 vocoder용 diffusion model인 InferGrad를 제안

 

• InferGrad
  
  • Reverse iteration을 통해 추론 schedule의 범위를 결정한 후, 해당 추론 schedule에 따라 random noise로부터 waveform을 생성
  • 생성된 waveform과 ground-truth 사이의 차이를 최소화하는 auxiliary loss를 추가적으로 활용
  • Loss는 waveform에 대한 amplitude와 phase information를 포함함

< Overall of Paper >

• 높은 합성 품질을 유지하면서도 추론 iteration 횟수를 효과적으로 줄인 diffusion vocoder
• 적은 수의 추론 step 만으로도 WaveGrad 이상의 성능을 달성
• 최적의 추론 schedule 탐색에 대한 필요를 줄이는 효율적인 추론 scheduling

2. Diffusion Probabilistic Model

• Diffusion model은 forward process와 reverse process로 정의됨
  1. Forward Process는:
     • $0 < \beta_{1} < ... < \beta_{T} < 1$인 pre-defined nosie schedule $\beta$에 따라 data sample $x_{0}$에 Gaussian noise $\epsilon \sim \mathcal{N}(0,I)$를 inject 하는 Markov Chain
     • 이때, 각 time step $t \in [1,...,T]$에서 transition probability는:
       (Eq.1) $q(x_{t} | x_{t-1}) = \mathcal{N} (x_{t} ; \sqrt{1-\beta_{t}} x_{t-1}, \beta_{t}I)$
     • DDPM과 Gaussian noise의 property를 통해, $x_{0}$에서 noisy data 분포 $q(x_{t}|x_{0})$를 얻을 수 있음:
       $q(x_{t}|x_{0}) = \mathcal{N} ( x_{t}; \sqrt{\bar{\alpha}_{t}}x_{0}, (1-\bar{\alpha}_{t})\epsilon)$
       - $\alpha_{t} := 1-\beta_{t}$
       - $\bar{\alpha}_{t} := \prod_{s=1}^{t} \alpha_{s}$는 time step $t$에서의  noise level
  2. Reverse Process는:
     • Data $x_{0}$를 재구성하기 위해, $p(x_{T}) \sim \mathcal{N}(0,I)$에서 noise를 점진적으로 제거하는 denoising process:
       (Eq.2) $p_{\theta} (x_{0}, ..., x_{T-1} | x_{T} ) = \prod_{t=1}^{T} p_{\theta} (x_{t-1} |x_{t})$
     • 이때 각 reverse step에 대한 transition probability는, $p_{\theta} (x_{t-1} |x_{t}) = \mathcal{N} (x_{t-1}, \mu_{\theta}(x_{t}, t), \sigma^{2}_{\theta} I)$로 parameterize 됨
       - 분산 $\sigma_{\theta}^{2}$은 $\frac{1-\bar{\alpha}_{t-1}} {1-\bar{\alpha}_{t}} \beta_{t}$ 또는 $\beta_{t}$로 predefine 됨
       - 평균 $\mu_{\theta}$는 $\mu_{\theta} (x_{t}, t) = 1/\sqrt{\alpha_{t}} (x_{t} - \beta_{t} / \sqrt{1-\bar{\alpha}_{t}} \epsilon_{\theta} (x_{t}, t))$로 나타낼 수 있음 
       - $\epsilon_{\theta} (x_{t}, t)$ : neural network estimated noise
  3. 최종적으로 model은 $p_{\theta} (x_{0})$의 variation lower bound를 최대화하여 학습됨
     - $\mu_{\theta}$에 대한 parameterization을 통한 training objective는:
     (Eq.3) $L_{D} (\theta) = \mathbb{E}_{x_{0}, \epsilon, t} || \epsilon - \epsilon_{\theta} ( \sqrt{ \bar{\alpha}_{t} }x_{0} + \sqrt{ 1- \bar{\alpha}_{t} }\epsilon, t)||_{2}^{2}$ 

3. InferGrad

• DDPM은 reverse process에서 사용되는 noise schedule $\hat{\beta}$가 forward process에서 정의되는 $\beta$와 다를 수 있음
  • 일반적으로 DDPM의 추론 속도를 향상하기 위해서는 diffusion step 수 $T$와 reverse step 수 $N$를 $N \ll T$로 설정함
    - 결과적으로 $N$이 상당히 작아지므로, noise schedule $\hat{\beta}$에 대한 선택이 중요함
  • BUT, 일반적인 DDPM trainig objective는 (Eq.3)과 같이 특정한 $\hat{\beta}$를 최대화하지 않음
  • 따라서 InferGrad는 $N$이 작을 때 DDPM의 sample 품질을 향상하는 것을 목표로 함
    1. 통합된 추론 schedule에 따른 random noise로부터 생성된 waveform과 ground-truth 사이의 차이를 최소화하는 infer loss를 도입
    2. Infer loss로부터 추론 schedule을 선택하는 방법을 논의

Overview of InferGrad

- Infer Loss 

• $N=T$일 때 DDPM의 reverse process는 diffsuion process의 반대로써, $x_{T}$에서 data sample $\hat{x}_{0}$를 생성
  • 이때, 빠른 sampling을 위해 $N \ll T$로 설정하면, 두 adjacent 추론 step 사이의 거리가 넓어지므로 생성 품질이 저하됨
    - InferGrad는 이를 위해, infer loss $L_{I}$를 사용하여 ground-truth $x_{0}$와 생성된 sample $\hat{x}_{0}$ 사이의 거리를 측정함
  • DDPM의 training objective에 $L_{I}$를 통합하면:
    (Eq. 4) $L = L_{D} (\theta) + \lambda L_{I} (x_{0}, \hat{x}_{0})$
    - $L_{D}$ : (Eq. 3), $\lambda$ : infer loss weight
  • $L_{I}$ 설계 시 고려사항:
    
    1. 각 time step $t$에서 ground-truth $x_{t}$를 정확하게 정의하는 것은 어렵기 때문에, intermediate latent representation $x_{t}$ 대신 ground-truth data $x_{0}$를 사용하여 거리를 계산
    2. Data $\hat{x}_{0}$는 추론 schedule $\hat{\beta}$를 통해 Gaussian noise $x_{T}$에서 생성됨
  • Infer loss를 통해 전체 reverse process가 model optimization에 통합될 수 있음
    - 결과적으로 $L_{I}$를 최소화하는 것은, DDPM의 sample 품질을 향상하는 것과 동일해짐
• $L_{I}$에 사용된 sample metric은 human perception과 관련이 높음
  • 여기서는 multi-resolution STFT를 $L_{I}$로 활용함:
    $L_{I} = \frac{1}{M} \sum_{m=1}^{M} L_{s}^{(m)}$
    - $L_{s}$ : single STFT loss, $M$ : resolution 수
    - 이때, magnitude와 phase information을 모두 사용하여 $L_{s}^{(m)}$에 대한 품질을 향상할 수 있음
  • 결과적으로 $x_{0}$과 $\hat{x}_{0}$에 대한 $L_{s}$는:
    (Eq.5) $L_{s} = \mathbb{E}_{x_{0}, \hat{x}_{0}} [ L_{mag} (x_{0}, \hat{x}_{0}) + L_{pha} (x_{0}, \hat{x}_{0})]$
    - $L_{mag}$ : mel-scaled log STFT magnitude spectrum의 $L_{1}$ loss
    - $L_{pha}$ : STFT phase spectrum의 $L_{2}$ loss

- Inference Schedules 

• 추론 step 수 $N$이 작을 때, DDPM sample 품질은 추론 schedule $\hat{\beta}$에 민감
  • InferGrad는 $L_{I}$에 $\hat{\beta}$의 범위를 포함시켜 추론 schedule에 대한 robustness를 향상
    - 적절한 범위를 결정하는 것은, 학습 안정성을 유지하고 추론을 개선하는데 도움을 줌
  • Vocoder task에 대해 $N \ll T$가 주어지면, 추론 scehduel $\hat{\beta}$를 결정하는 것이 필요
    - Diffusion process가 $0 < \beta_{1} < ... < \beta_{t} <1$의 학습 schedule을 통해 data를 Gaussian noise $\mathcal{N}(0,I)$로 변환한다고 가정하면,
    - $\bar{\alpha}_{t} = \prod_{s=1}^{t} (1-\beta_{s})$은 $t=0$에서 1, $t=T$에서 0의 사이의 범위를 가지는 noise level
  • 학습 과정에서 사용되는 $\beta, \bar{\alpha}$를 기반으로, 추론에 사용되는 schedule $\hat{\beta}$와 $\hat{\bar{\alpha}}$를 아래와 같이 결정
    1. $\hat{\beta}$의 범위
       - $\hat{\beta}$는 $\beta_{1} \leq \hat{\beta_{1}} < ... < \hat{\beta}_{N} < 1$을 따름
       - $\beta_{1}$은 학습에 사용되는 minimum noise scale
       - $N \ll T$일 때, $\hat{\beta}_{N}$은 $\hat{\bar{\alpha}}_{N}$이 적절한 범위에 위치하는 것을 보장하기 위해 $\beta_{T}$보다 큰 값을 가짐
    2. $\hat{\beta}_{n}$과 $\hat{\beta}_{n-1}$ 사이의 비율
       - $\hat{\beta}$ 결정 시, $\hat{\beta}_{N}$에서 시작하여 $\hat{\beta}_{1}$으로 결정하는 것이 좋음
       - 이때, DDPM의 denoising 능력을 보장하기 위해서는 $\hat{\beta}_{n}$과 $\hat{\beta}_{n-1}$ 사이의 비율이 너무 크면 안 됨
       - 논문에서는 $\frac{\hat{\beta}_{n}} {\hat{\beta}_{n-1}} > 10^{3}$으로 설정
    3. $\hat{\bar{\alpha}}_{N}$의 값
       - $\mathcal{N}(0,I)$에서 reverse process를 시작할 때, $\hat{\bar{\alpha}}_{N} \in [\bar{\alpha}_{T}, 1)$은 1에 가까운 값을 가지면 안 됨
       - DDPM은 첫 번째 reverse step에서 $\bar{\alpha}_{T} \approx 0$에서 $\hat{\bar{\alpha}}_{N}$까지 도달해야 하기 때문
       - 따라서, $\hat{\bar{\alpha}}_{N}$이 1에 가까우면, DDPM의 denoising이 충분하지 못해 sample에 distortion이 발생할 수 있음
       - 논문에서는 0.7 이하의 값을 권장
  • 결과적으로 학습 과정에서 특정한 $\hat{\beta}$ 대신 $\hat{\beta}$의 범위를 고려함으로써, 추론 과정에서 $\hat{\beta}$ 선택에 대한 robustness를 확보
    - 추가적으로 최적의 $\hat{\beta}$를 찾기 위해, grid search를 사용할 수도 있음

4. Experiments

- Settings

• Dataset : LJSpeech
• Comparisons : WaveGrad

- Results

• InferGrad는 동일한 추론 step에 대해 WaveGrad 보다 0.28의 MOS 향상이 있음
  - 비슷한 합성 품질을 보이는 6-step WaveGrad와 2-step InferGrad의 추론 속도를 비교해 보면, InferGrad가 3배의 추론 가속 효과를 보임

합성 품질 비교

• 합성된 sample에 대한 mel-spectrogram을 비교해보면, InferGrad가 ground-truth와 비슷한 mel-spectrogram을 합성하는 것을 확인할 수 있음

합성된 mel-spectrogram 비교

• 정량적인 성능 비교에서도, InferGrad가 WaveGrad 보다 우수한 성능을 보임

정량적인 성능 비교

• 특정한 추론 step을 정해서 추론했을 때도, 일반적인 InferGrad 추론과 큰 차이를 보이지 않음
  - InferGrad는 특정 iteration에 대해서도 적합한 추론 schedule을 고려할 수 있기 때문

일반 추론과 지정된 추론 step 간의 CMOS 비교

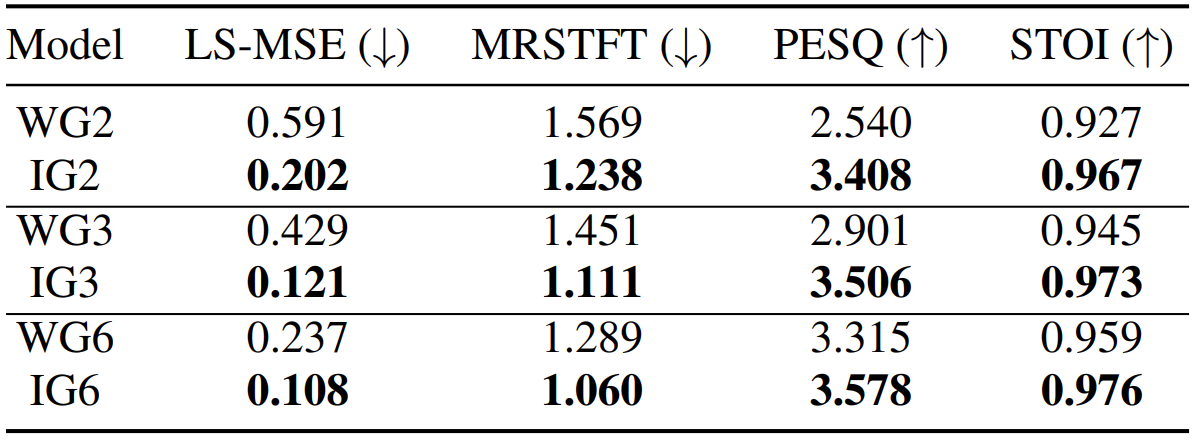
• Model Sensitivity
  • $\hat{\beta}$ 설정에 따른 합성된 sample의 평균 품질을 비교
    - 평균은 $\hat{\beta}$ 선택 별로 생성된 sample의 평균 품질
    - 표준편차는 값이 클수록 $\hat{\beta}$에 민감하다는 것을 의미
  • 추론 step 수를 줄이면 WaveGrad의 경우 생성 품질이 크게 저하되고, $\hat{\beta}$ 선택에 민감해짐
  • InferGrad의 경우, 각 설정과 관계없이 꾸준히 높은 성능을 보이고 상대적으로 $\hat{\beta}$의 영향을 받지 않음

Sensitivity 비교 결과

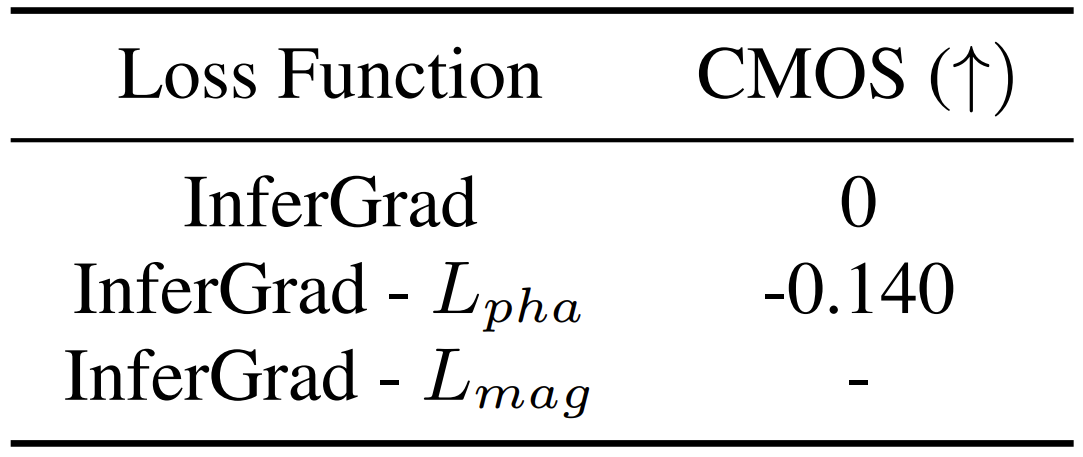
• Ablation Study
  • InferGrad는 magnitude loss와 phase loss 모두를 활용함
  • Phase loss를 제거하는 경우, 합성된 sample에 대한 artifact가 남아있어 magnitude loss의 최적화를 방해함
    - 결과적으로 성능을 저하시킴

Ablation Study 결과