[Paper 리뷰] PeriodGrad: Towards Pitch-Controllable Neural Vocoder based on a Diffusion Probabilistic Model

PeriodGrad: Towards Pitch-Controllable Neural Vocoder based on a Diffusion Probabilistic Model

---

• Diffuision-based vocoder는 고품질의 합성이 가능하고 간단한 time-domain loss로 학습할 수 있지만 pitch control이 어려움
  
• PeriodGrad
  • Explicit periodic signal을 auxiliary conditioning signal로써 Denoising Diffusion Probabilistic Model에 통합
  • Waveform의 periodic structure를 정확하게 capture 하여 pitch controllability를 향상
• 논문 (ICASSP 2024) : Paper Link

---

1. Introduction

• Neural vocoder의 성능은 합성된 음질, 추론 속도, controllability 측면에 크게 좌우됨 
  • Neural vocoder는 크게 Autoregressive (AR), Non-AR 방식으로 나눠짐
    1. 대표적으로 Generative Adversarial Network (GAN)을 활용하는 방식이 주목받고 있음
       - BUT, 여러 auxiliary loss가 필요하기 때문에 training이 복잡하다는 단점이 있음
    2. Denoising Diffusion Probabilistic Model (DDPM)은 GAN-based 방식 보다 뛰어난 성능을 보이고 있음
       - 높은 합성 품질을 달성하면서 간단한 time-domain loss로 학습될 수 있다는 장점
       - BUT, 추론 시 iterative denoising process로 인해 추론 속도의 한계가 있음
  • 한편으로 neural vocoder는 data-driven approach이기 때문에 기존 signal processing-based vocoder보다 controllability가 떨어지는 문제가 있음
    - 특히 fundamental frequency $F_{0}$에 대한 controllability는 가장 핵심적인 문제임
  • 이를 해결하기 위해 GAN-based vocoder는 pitch에 해당하는 sinusoidal signal을 explicit periodic signal로 제공하는 방식이 도입되었음
    - BUT, DDPM-based vocoder에는 아직 이러한 방식들이 도입되지 않아 pitch controllability가 떨어짐

-> 그래서 explicit periodic signal을 반영하는 DDPM-based vocoder인 PeriodGrad를 제안

 

• PeriodGrad
  • PriorGrad를 기반으로 explicit periodic signal을 conditioning
  • Adaptive prior를 통해 합리적인 추론 비용을 유지하면서 $F_{0}$ controllability를 향상 가능

< Overall of PeriodGrad >

• Explicit periodic signal을 auxiliary conditioning signal로써 PriorGrad에 통합
• 결과적으로 기존 DDPM-based vocoder 보다 우수한 합성 품질을 달성

2. DDPM-based Neural Vocoder

• $\mathbf{x}_{0}=(x_{1},x_{2},...,x_{N})$을 acoustic feature sequence $\mathbf{c}= (c_{1},c_{2},...,c_{K})$에 대응하는 speech waveform이라고 하자
  • $N$ : speech waveform의 sample 수, $K$ : acoustic feature의 frame 수 
  • 그러면 neural vocoder는 acoustic feature sequence $\mathbf{c}$에 대한 speech waveform $\mathbf{x}_{0}$의 sample sequence를 생성하는 DNN으로 정의할 수 있음

- Overview of DDPM

• DDPM은 2개의 Markov chain (forward/reverse process)로 정의된 deep generative model
  1. Forward process는
     • Data $\mathbf{x}_{0}$를 standard noise $\mathbf{x}_{T}$로 점진적으로 diffuse 함:
       (Eq. 1) $q(\mathbf{x}_{1:T}|\mathbf{x}_{0})=\prod_{t=1}^{T}q(\mathbf{x}|\mathbf{x}_{t-1})$
       - $T$ : DDPM의 step 수, $q(\mathbf{x}_{t}| \mathbf{x}_{t-1}) = \mathcal{N}(\mathbf{x}_{t};\sqrt{1-\beta_{t}}\mathbf{x}_{t-1},\beta_{t}I)$ : pre-defined noise schedule $\{ \beta_{1},...,\beta_{T}\}$에 따라 Gaussian noise를 추가하는 transition probability
     • (Eq. 1)을 통해 arbitrary time step $t$에서 closed form으로 $\mathbf{x}\sim q(\mathbf{x}_{t}| \mathbf{x}_{0})$를 sample 할 수 있음:
       (Eq. 2) $\mathbf{x}_{t}=\sqrt{\bar{\alpha}_{t}}\mathbf{x}_{0}+\sqrt{1-\bar{\alpha}_{t}}\epsilon$
       - $\alpha_{t}=1-\beta_{t}, \bar{\alpha}_{t}=\prod_{s=1}^{t}\alpha_{s}, \epsilon\sim \mathcal{N}(0,I)$
  2. Reverse process는
     • Standard noise $p(\mathbf{x}_{T})$로부터 data $\mathbf{x}_{0}$를 점진적으로 생성하는 denoising process:
       (Eq. 3) $p_{\theta}(\mathbf{x}_{0:T})=p(\mathbf{x}_{T})\prod_{t=1}^{T}p_{\theta}(\mathbf{x}_{t-1}| \mathbf{x}_{t})$
       - $p_{\theta}(\mathbf{x}_{t-1}|\mathbf{x}_{t})$ : parameter $\theta$를 가지는 DNN으로 modeling 됨
     • $\beta_{t}$가 작을 때 forward/reverse process 모두 동일한 function form을 가지므로, reverse process의 transition probability는 $p_{\theta}(\mathbf{x}_{t-1}| \mathbf{x}_{t})=\mathcal{N}(\mathbf{x}_{t-1};\mu_{\theta}(\mathbf{x}_{t},t),\gamma_{t}I)$로 parameterize 됨
       - $\gamma_{t}=\frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_{t}}\beta_{t}$, $\gamma_{1}=0$
     • 이때 평균 $\mu_{\theta}(\mathbf{x}_{t},t)$는:
       (Eq. 4) $\mu_{\theta}(\mathbf{x}_{t},t)=\frac{1}{\sqrt{\alpha}_{t}}\left( \mathbf{x}_{t}-\frac{\beta_{t}}{\sqrt{1-\bar{\alpha}_{t}}}\epsilon(\mathbf{x}_{t},\mathbf{c},t)\right)$
       - $\epsilon_{\theta}(\mathbf{x}_{t},\mathbf{c},t)$ : $\mathbf{x}_{t}$에 포함된 noise를 예측하는 DNN
  3. DDPM은 $\mathbf{x}_{1:T}$를 latent variable로 하는 latent variable model로 볼 수 있음
     • 따라서 모델 $\epsilon_{\theta}(\mathbf{x}_{t},\mathbf{c},t)$는 log-likelihood $p(x_{0})$의 Evidence Lower BOund (ELBO)를 최대화하여 최적화됨
     • 이때 DDPM-based vocoder는 일반적으로 아래의 simplified loss $L_{DDPM}(\theta)$을 사용:
       (Eq. 5) $L_{DDPM}(\theta)=\mathbb{E}_{q}\left[ || \epsilon -\epsilon_{\theta}(\mathbf{x}_{t},\mathbf{c},t)||_{2}^{2} \right]$
       - $|| \cdot ||_{p}$ : $L_{p}$ norm

- PriorGrad

• DDPM-based vocoder인 WaveGrad와 DiffWave는 충분한 음성 품질을 달성하기 위해 200회 이상의 iteration이 필요함
  • PriorGrad는 이 문제를 해결하기 위해 adaptive prior $\mathcal{N}(0,\Sigma_{c})$를 도입
  • Diagonal variance $\Sigma_{c}$는 $\mathbf{c}$에서 $\Sigma =\mathrm{diag}[(\sigma_{1}^{2},\sigma_{2}^{2},..., \sigma_{N}^{2})]$로 계산됨
    - $\sigma_{n}^{2}$ : $\mathbf{c}$에서 계산된 normalized frame-level energy를 interpolate 하여 얻어진 $n$-th sample의 power
  • 이때 loss function은 $\Sigma_{c}$에 따른 Mahalanobis distance를 사용함:
    (Eq. 6) $L_{Prior}(\theta)=\mathbb{E}_{q}\left[ || \epsilon-\epsilon_{\theta}(\mathbf{x}_{t},\mathbf{c},t)||^{2}_{\Sigma_{c}^{-1}}\right]$
    - $|| \mathbf{x}||^{2}_{\Sigma^{-1}} = \mathbf{x}^{\top}\Sigma^{-1}\mathbf{x}$
  • 직관적으로, adaptive prior의 power envelope가 standard Gaussian prior의 power envelope 보다 target speech waveform에 더 가깝기 때문에 PriorGrad는 더 나은 denoising 성능과 빠른 추론 속도를 보임

3. Method

• Speech waveform은 strongly autocorrelated signal로써 이미지와는 본질적으로 다른 characteristic을 가짐
  • DDPM-based vocoder는 오직 data-driven 방식으로 periodic structure를 학습하므로 $F_{0}$ controllability가 제한됨
    - 특히 적은 training data와 높은 sampling rate에 대해서는 periodic speech의 생성이 까다로움
  • 따라서 explicit periodic information을 사용하면 DDPM-based vocoder의 controllability를 향상할 수 있음
• PeriodGrad는 explicit periodic signal을 condition으로 활용하는 DDPM-based vocoder
  • Extended noise estimation model $\epsilon_{\theta}(\mathbf{x}_{t},\mathbf{c},\mathbf{e},t)$는 auxiliary feature $\mathbf{c}$와 periodic signal $\mathbf{e}=[e_{1},e_{2},...,e_{N}]$를 condition으로 하여 input signal $\mathbf{x}_{t}$를 denoise 함
  • 이때 sine wave와 voiced/unvoiced (V/UV) signal이 concatenate 된 sample-level signal을 periodic signal $e$로 사용
    - 여기서 additional condition embedding layer를 도입하기만 하면 모든 model structure를 활용할 수 있음
    - 즉, (Eq. 5), (Eq. 6)과 같은 DDPM-based vocoder와 동일한 training criterion을 사용하여 학습될 수 있음
  • 결과적으로 PeriodGrad는 PriorGrad를 기반으로 energy-based adaptive prior를 채택하고, 다음의 loss를 따라 학습됨:
    (Eq. 7) $L_{Period}(\theta)=\mathbb{E}_{q}\left[ || \epsilon - \epsilon_{\theta}(\mathbf{x}_{t}, \mathbf{c},\mathbf{e},t)||^{2}_{\Sigma_{c}^{-1}}\right]$

4. Experiments

- Settings

• Dataset : Japaese Children's Songs
• Comparisons : PriorGrad, PeriodNet

- Results

• Objective Evaluation
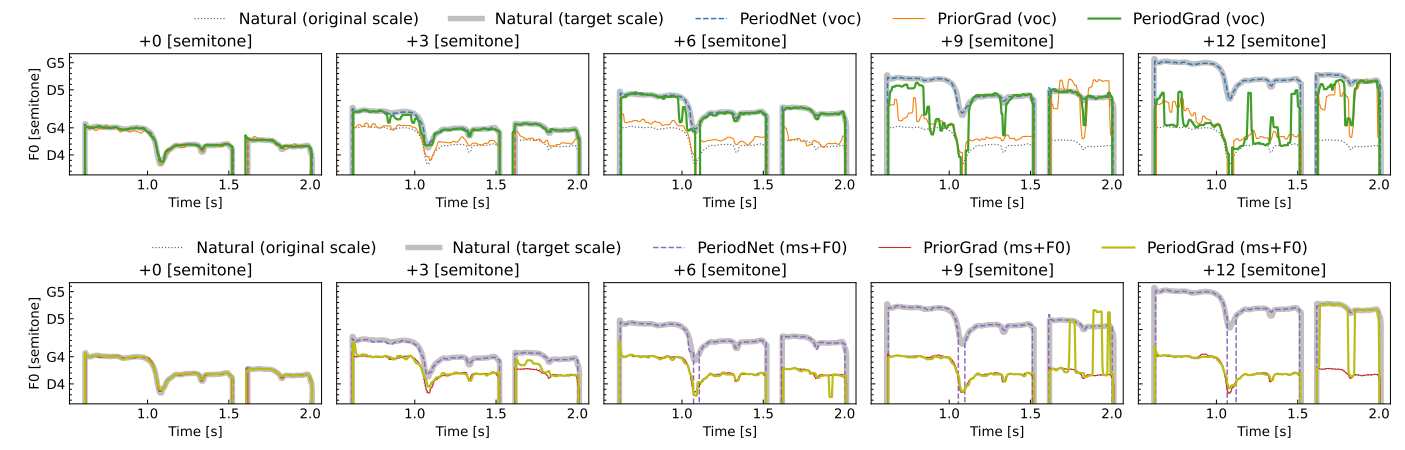
  • 생성된 waveform에서 추출된 $\log F_{0}$를 확인해 보면
  • PeriodGrad가 PriorGrad보다 주어진 $\log F_{0}$를 더 정확하게 reproducing 함
    - 즉, explicit periodic signal을 사용하면 DDPM-based vocoder의 $F_{0}$ controllability를 향상 가능

$F_{0}$ Accuracy 비교

• 한편 $F_{0}$가 6 semitone 이상 shift 되는 경우, PeriodGrad를 사용하더라도 $F_{0}$-RMSE가 저하되는 것으로 나타남
  
  • 추출된 $F_{0}$에 octave confusion이나 V/UV detection error가 존재할 수 있기 때문
  • 추출된 $F_{0}$의 unvoiced region은 continuous feature로 linearly interpolate 되기 때문
    - 결과적으로 모델이 explicit 하게 주어진 $F_{0}$보다 mel-spectrogram을 더 신뢰하게 됨

생성된 음성의 $F_{0}$ Contour

• Subjective Evaluation
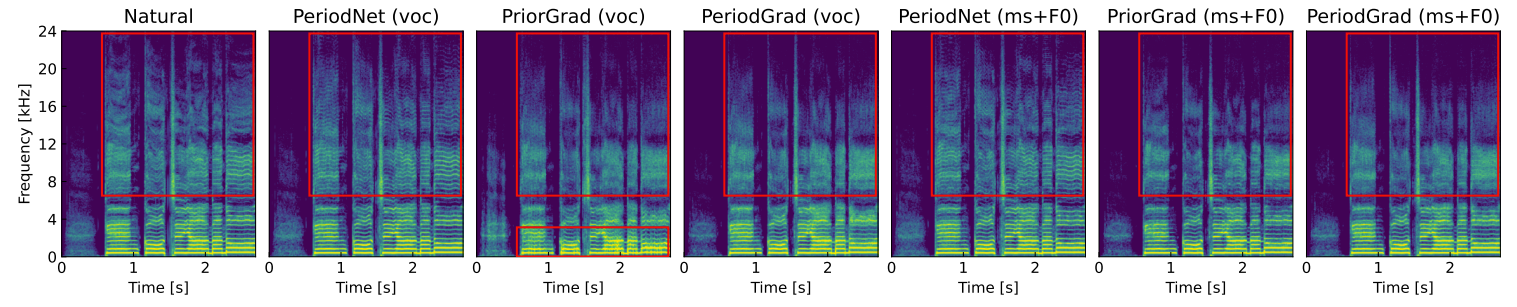
  • MOS 측면에서 합성 품질을 비교해 보면 PeriodGrad가 PriorGrad 보다 뛰어난 품질을 보임
  • 특히 normalized energy를 사용하는 PeriodGrad (ms-F0)는 경우, mel-spectrogram의 low-frequency range에서 unnatural fluctuation이 나타나지 않음

합성 품질 비교

Mel-Spectrogram 비교