[Paper 리뷰] EfficientTTS: An Efficient and High-Quality Text-to-Speech Architecture

EfficientTTS: An Efficient and High-Quality Text-to-Speech Architecture

---

• Text-to-Speech를 위해 non-autoregressive architecture는 많은 이점을 가지고 있음
• EfficientTTS
  • External aligner를 필요로 하는 autoregressive 모델과 달리, 안정적인 end-to-end 학습을 지원하여 효율적이면서 고품질의 음성 합성이 가능
  • 연산량을 증가시키지 않고, sequence alignment에 monotonic constraint를 반영할 수 있는 monotonic alignment modeling을 제시
  • EfficientTTS를 다양한 feed-forward network 구조와 결합하여 Text-to-Mel-spectrogram, Text-to-Waveform 모두를 지원
• 논문 (ICML 2021) : Paper Link

---

1. Introduction

• Text-to-Speech (TTS)는 encoder-decoder framework를 기반으로 하는 autoregressive 모델을 주로 활용함
  • Autoregressive framework에서
    - Encoder는 text sequence를 input으로 사용하여 hidden representation을 학습
    - Decoder는 frame-by-frame과 같이 autoregressive 방식으로 output을 생성
  • Autoregressive 모델은 합성 품질은 우수하지만 합성 속도가 느리다는 단점이 존재
  • 이때 non-autoregressive TTS는 autoregressive 방식의 한계를 개선할 수 있음
    -> BUT, 복잡한 학습 과정으로 실적용이 어렵다는 단점이 존재

-> 그래서 효율적이면서 고품질의 TTS 작업이 가능한 non-autoregressive 모델인 EfficientTTS를 제안

 

• EfficientTTS
  • Fully parallel하고, end-to-end로 학습되는 non-autoregressive TTS 모델
    - 결과적으로 학습/추론 속도 모두를 향상 가능
  • Soft/hard monotonic alignment를 통해 sequence alignment를 monotonic 하게 제한하고, 연산량의 증가 없이 vanilla attention mechanism을 확장
    - Network 구조에 관계없이 모든 attention mechanism에 통합 가능

< Overall of EfficientTTS >

• Additional aligner 없이 text sequence로부터 고품질의 음성 합성을 수행하는 non-autoregressive arhictecture
• Sequence-to-Sequence 모델에 대한 새로운 soft/hard monotonic alignment를 제시
• Convolutional, Flow-based, End-to-End 방식으로 EfficientTTS를 확장하여, 품질 및 학습/추론 효율성 모두가 향상됨을 보임

2. Related Work

- Non-Autoregressive TTS Models

• TTS에서 input text sequence $x = [x_{0}, x_{1}, ..., x_{T_{1}-1}]$은 encoder-decoder framework를 통해 output sequence $y=[y_{0}, y_{1}, ..., y_{T_{2}-1}]$로 변환됨
  • $x$는 encoder $f: h = f(x)$를 통해 hidden state sequence $h=[h_{0}, h_{1}, ..., h_{T_{1}-1}]$로 변환된 다음, decoder를 통과하여 output $y$를 생성함
    1. 이때 각 output timestep에 대해 attention mechanism을 적용하여 $h$의 모든 element를 search하고 context vector $c$를 생성할 수 있음:
       (Eq. 1) $c_{j} = \sum_{i=0}^{T_{i}-1}\alpha_{i,j}*h_{i}$
       - $\alpha \in \mathcal{R}^{(T_{1}, T_{2})}$ : alignment matrix
       
    2. 이후 $c$는 다른 network $g$에 공급되어 output $y: y= g(c)$를 생성
       - 여기서 $f, g$ network는 동일한 length의 input, output을 사용하기 때문에 parallel 구조로 쉽게 대체할 수 있음
  • 따라서 non-autoregressive TTS 모델 구축을 위해서는 parallel alignment prediction이 가장 중요함
    -> 이를 위해 EfficientTTS는 single network를 통해 안정적인 학습을 유지하면서 sequence alignment 및 음성 생성을 jointly learning

- Monotonic Alignment Modeling

• 일반적인 attention mechanism은 모든 output timestep에 대해 모든 input step을 inspect 함
  • 이때 long sequence의 경우 학습하는데 비용이 많이 소모되고, misalignment가 자주 발생함
  • 특히 alignment는 다음과 같은 strict criteria를 따라야 함
    1. Monotonicity : 각 output timestep에서 aligned position은 절대 rewind 되지 않음
       
    2. Continuity : 각 output timestep에서 aligned position은 one step forward로만 이동할 수 있음
    3. Completness : Aligned position은 input token의 모든 position을 cover 해야 함
  • Alignment를 위한 방법들이 제안되었지만, 대부분 sequential step을 필요로 하고 위의 조건을 충족시키지 못함
    -> 따라서 EfficientTTS에서는 monotonic alignment를 위한 새로운 approach를 제시

Monotonic Alignment

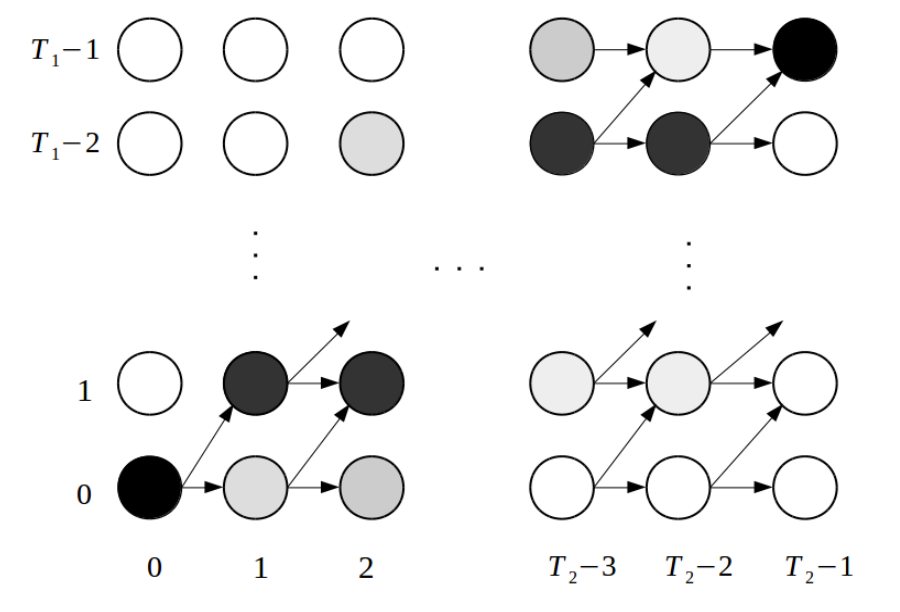
3. Monotonic Alignment Modeling Using IMV

• Monotonic alignment modeling을 위해 Index Mapping Vector (IMV)를 제안

- Definition of IMV

• $\alpha \in \mathcal{R}^{(T_{1},T_{2})}$를 input sequence $x \in \mathcal{R}^{T_{1}}$과 output sequence $y \in \mathcal{R}^{T_{2}}$ 사이의 alignment라 하자
  • Index Mapping Vector (IMV) $\pi$는 $\alpha$로 weighting 된 index vector $p = [0,1, ..., T_{1}-1]$의 sum으로:
    (Eq. 2) $\pi_{j} = \sum_{i=0}^{T_{i}-1} \alpha_{i,j}*p_{i}$
    - $0\leq j \leq T_{2}-1$, $\pi \in \mathcal{R}^{T_{2}}$, $\sum_{i=0}^{T_{i}-1} \alpha_{i,j} = 1$ 
  • IMV는 각 output timestep의 expected location으로 볼 수 있음
    - 이때 expectation은 $0$에서 $T_{1}-1$까지의 가능한 모든 input location

- Monotonic Alignment Modeling Using IMV

• Continuity and Monotonicity
  • 주어진 alignment matrix $\alpha$가 continuity와 monotonicity ciriteria를 충족한다고 하면:
    (Eq. 3) $0\leq \Delta \pi_{i} \leq 1$
  • $\Delta \pi_{i} = \pi_{i} - \pi_{i-1}$, $1 \leq i \leq T_{2}-1$ 
• Completeness
  • $\pi$가 timestep 전반에 대해 continuous하고 montonic하다면, completeness criteria는 아래 boundary constraint와 동치:
    (Eq. 4) $\pi_{0} = 0$
    (Eq. 5) $\pi_{T_{2}-1} = T_{1}-1$
  • $\alpha_{0} = [1, 0, ..., 0], \alpha_{T_{2}-1} = [0, 0, ..., 1]$로부터 deduce 될 수 있음

- Incorporate IMV into Network

• IMV를 sequence-to-sequence network에 incorporate 하기 위해 아래 2가지 방식을 제시
  1. Soft Montonic Alignment (SMA)
     • Sequence-to-Sequence 모델을 (Eq. 3~5)의 constraint하에서 학습하기 위해, 해당 constraint를 training objective로 고려
     • 따라서 constraint를 다음과 같은 SMA loss로 표현하면:
       (Eq. 6) $\mathcal{L}_{SMA} = \lambda_{0}||\, |\Delta_{\pi}| -\Delta \pi ||_{1} + \lambda_{1} || \, |\Delta \pi-1|+(\Delta \pi-1)||_{1} +\lambda_{2} \left( \frac{\pi_{0}}{T_{1}-1}\right)^{2} + \lambda_{3} \left( \frac{\pi_{T_{2}-1}}{T_{1}-1}-1\right)^{2}$
       - $|| \cdot ||_{1}$ : $\ell^{1}$ norm
       - $\lambda_{0}, \lambda_{1}, \lambda_{2}, \lambda_{3}$ : positive coefficient
       - $\mathcal{L}_{SMA}$는 non-negative이고, $\pi$가 모든 constraint를 충족하는 경우에만 0
     • 이때 index vector $p$는 always known이므로, $\mathcal{L}_{SMA}$ 계산에는 alignment matrix $\alpha$만 필요
       - 결과적으로 network의 구조 변경 없이도 SMA loss를 sequence-to-sequence network에 incorporate 할 수 있음
     • 일반적으로 SMA는 Guided Attention과 유사한 역할을 수행함
       - BUT, SMA는 alignment에 대해 더 엄밀한 constraint를 제공하므로 Guided Attention보다 뛰어난 성능을 보임
  2. Hard Monotonic Alignment (HMA)
     • SMA를 사용하면 network가 monotonic alignment를 학습할 수 있지만, 학습 초기에서 monotonic alignment를 생성할 수 없기 때문에 많은 비용이 필요함
       - 따라서 Hard Montonic Alignment (HMA)를 통해 supervision 없이 monotonic alignment를 생성
     • 먼저 (Eq. 2)에 따라 alignment matrix $\alpha$로부터 IMV $\pi'$를 계산하자
       - 이렇게 얻어진 $\pi'$는 monontonic 하지 않지만, ReLU activation을 통해 $\Delta \pi \geq 0$을 적용하면 strictly monotonic IMV $\pi$로 변환됨:
       (Eq. 7) $\Delta \pi'_{j} = \pi'_{j}-\pi'_{j-1}, \,\,\, 0 < j \leq T_{2}-1 $
       (Eq. 8) $\Delta \pi_{j} = ReLU(\Delta \pi'_{j}), \,\,\, 0 < j \leq T_{2}-1$
       (Eq. 9) $\pi_{j} = \sum_{m=0}^{j}\Delta \pi_{m}, \,\,\, 0 \leq j \leq T_{2}-1, \, \Delta \pi_{0} = 0$
       
     • $\pi$의 domain을 (Eq. 4~5)에서 주어진 interval $[0, T_{1}-1]$로 restrict 하고, $\pi$에 positive scalar를 multiply 하면:
       (Eq. 10) $\pi^{*}_{j} = \pi_{j} * \frac{T_{1}-1}{\max(\pi)} = \pi_{j} * \frac{T_{1}-1}{\pi_{T_{2}-1}}$
       - $\pi$의 최대값은 timestep에 걸쳐 monotonic 하게 증가하므로 $\pi_{T_{2}-1}$
     • 이후 monotonic alignment를 구성하기 위해, $\pi^{*}$로 centered 된 Gaussian kernel을 적용하여 alignment를 reconstruction 하는 transformation을 얻음:
       (Eq. 11) $\alpha'_{i,j} = \frac{\exp (-\sigma^{-2}(p_{i}-\pi^{*}_{j})^{2})}{\sum_{m=0}^{T_{1}-1} \exp(-\sigma^{-2}(p_{m}-\pi_{j}^{*})^{2})}$
       - $\sigma^{2}$ : alignment variation을 나타내는 hyperparameter
       - $\alpha'$ : 기존 alignment $\alpha$를 대체
       - 이때 $\alpha'$과 $\alpha$의 차이점은, $\alpha'$은 monotonicity가 보장되지만 $\alpha$는 monotonicity에 대한 constraint가 없다는 것
     • HMA는 monotonic alignment 학습의 어려움을 줄여 학습 효율성을 향상할 수 있음
       - SMA와 마찬가지로 HMA도 sequence-to-sequence network에 incorporate 가능함
       -> 결과적으로 EfficientTTS는, 이러한 HMA 기반의 internal aligner를 통해 strict monotonic constraint 하에서 빠르고 효율적인 network 학습이 가능

4. EfficientTTS Architecture

• EfficientTTS의 동작과정을 요약하면
  • 학습 단계에서는
    1. IMV generator를 통해 text sequence와 mel-spectrogram의 hidden representation으로부터 IMV를 계산
       - 이때 Text sequence와 mel-spectrogram의 hidden representation은 각각 text-encoder와 mel-encoder로 얻어짐
    2. 이후 IMV는 alignment reconstruction layer를 통해 time-aligned representation을 생성하기 위한 2-dimensional alignment matrix로 변환됨
    3. 마지막으로 time-aligned representation은 output mel-spectorgram/waveform을 생성하는 decoder로 전달됨
       - 이 과정에서 각 input text token에 대한 aligned position을 예측하는 aligned position predictor를 cocurrently train 함
  • 추론 단계에서는, 예측된 aligned position으로부터 alignment를 reconstruct

Overall of EfficientTTS

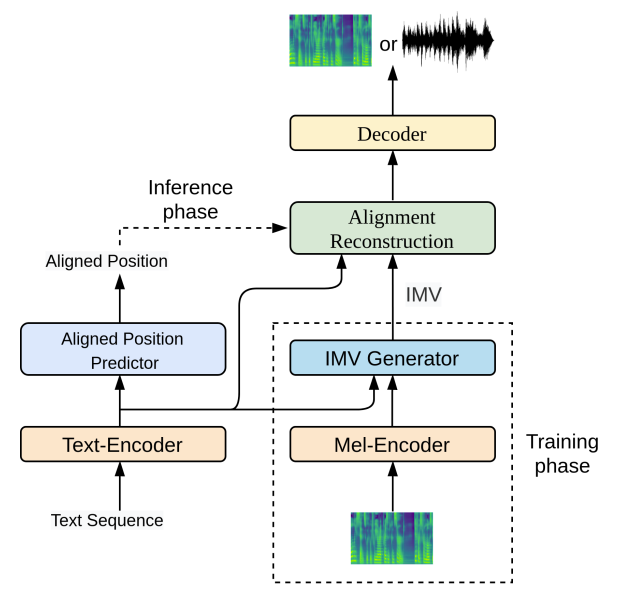
- Text-Encoder and Mel-Encoder

• Text-encoder와 Mel-encoder를 사용하여 text symbol과 mel-spectrogram을 각각 hidden representation으로 변환
  • Text-encoder는 FastSpeech의 구조를 채택
    - Text embedding layer와 transformer FFT block stack으로 구성
    - 특히 transformer FFT block을 사용하면 text encoder가 local/global information을 모두 학습할 수 있어 alignment prediction에 유용함
  • Mel-encoder는 
    - Linear projection을 통해 mel-spectrogram을 high-dimensional vector로 변환
    - 이후 weight normalization, Leaky ReLU, reisdual connection을 포함한 convolution stack을 적용
    - Mel-encoder는 학습 단계에서만 사용됨

- IMV Generator

• Monotonic IMV를 생성하기 위해, 아래 (Eq. 12)와 같이 scaled dot-product attention으로 input과 output 간의 alignment $\alpha$를 학습
  • 즉, $\alpha$로부터 IMV의 계산은:
    (Eq. 12) $\alpha_{i,j} = \frac{\exp (-D^{-0.5}(q_{j}\cdot k_{i}))}{\sum_{m=0}^{T_{1}-1} \exp(-D^{-0.5}(q_{j}\cdot k_{m}))}$
    - $q$ : mel-encoder output, $k$ : text-encoder output
    - $D$ : $q,k$의 dimensionality
  • 이때 각 timestep $j$에서 $\Delta \pi$를 forward/backward direction으로 아래와 같이 accumulate 할 수 있음:
    (Eq. 13) $\pi_{j}^{f} = \sum_{m=0}^{j}\Delta \pi_{m}, \,\, \pi_{j}^{b}=\sum_{m=j}^{T_{2}-1}\Delta \pi_{m}$
    (Eq. 14) $\pi_{j} = \pi_{j}^{f}-\pi_{j}^{b}$
    - (Eq. 14)에 따라 $\pi$는 timestep 전반에 걸쳐 monotonic 하게 증가하므로 $\pi$의 최소값은 $\pi_{0}$이고 최대값은 $\pi_{T_{2}-1}$
  • 따라서 linear transformation을 통해 $\pi$를 interval $[0, T_{1}-1]$로 restrict 하면:
    (Eq. 15) $\pi_{j}^{*}= \frac{\pi_{j}-\pi_{0}}{\pi_{T_{2}-1}-\pi_{0}}*(T_{1}-1)$

- Aligned Position Predictor

• 추론 단계에서 모델이 text sequence의 hidden representation $h$로부터 IMV $\pi$를 직접 예측하는 것은 어려움
  • 아래 2가지의 한계 때문:
    1. $\pi$는 time-aligned이고, high-resolution인 반면, $h$는 low-resolution임
    2. $\pi_{i}$의 각 예측은 (Eq. 9)의 cumulative sum operation으로 인해 이후 $\pi_{j} \, (j>i)$ 예측에 영향을 미치므로, $\pi$를 parallel 하게 예측하기 어려움
  • 이때 각 input token의 aligned position $e$를 대신 예측하는 것으로 위의 한계점을 극복할 수 있음
    1. 이를 위해 $q = [0,1,..., T_{2}-1]$을 $\pi$의 index vector라고 하자
    2. 그러면 transformation $m(\cdot)$을 $\pi, q$ 사이의 mapping $\pi = m(q)$으로 정의할 수 있음
    3. 이때 $\pi$는 $q$에 대해 monotonic 하게 증가하므로, $m(\cdot)$은 monotonic transformation이고, invertible 함:
       (Eq. 16) $q = m^{-1}(\pi)$
       
    4. 따라서 각 input token의 output timestep에서 aligned position $e$는:
       (Eq. 17) $e = m^{-1}(p), \,\, p = [0,1,...,T_{1}-1]$
    5. 이후 $e$를 계산하기 위해 (Eq. 11)과 유사한 transformation을 사용하여 probability density matrix $\gamma$를 계산:
       (Eq. 18) $\gamma_{i,j} = \frac{\exp(-\sigma^{-2}(p_{i}-\pi_{j})^{2})}{\sum_{n=0}^{T_{2}-1}\exp (-\sigma^{-2}(p_{i}-\pi_{n})^{2})}$
    6. 결과적으로 aligned position $e$는 $\gamma$로 weighted 된 output index vector $q$의 weighted sum:
       (Eq. 19) $e_{i} = \sum_{n=0}^{T_{2}-1}\gamma_{i,n}*q_{n}$
  • 위와 같이 $e$의 계산은 differentiable 하기 때문에 gradient를 통해 학습할 수 있음
    - 이때 $e$는 predictable 함
    1. $e$와 $h$의 resolution이 동일하기 때문
    2. $e$를 직접 학습하지 않고 relative position $\Delta e\,\, (\Delta e_{i} = e_{i}- e_{i-1}, \, 1\leq i \leq T_{1}-1)$을 학습할 수 있기 때문
• Aligned position predictor는
  • 2개의 convolution으로 구성되고 각 convolution은 layer noramlization과 ReLU activation을 포함
  • 이때 $\pi$로부터 계산된 $\Delta e$를 training target으로 하고, 추정된 position $\Delta \hat{e}$와 target $\Delta e$ 사이의 loss function은:
    (Eq. 19) $\mathcal{L}_{ap} = || \log (\Delta \hat{e}+\epsilon)- \log (\Delta e + \epsilon)||_{1}$
    - $\epsilon$ : numerical instability를 해결하기 위한 small number
  • Aligned position predictor는 모델의 나머지 부분들과 함께 jointly learning 됨
    - 결과적으로 EfficientTTS는 aligend position을 통해 alignment를 생성하기 때문에 duration-based non-autoregressive TTS 모델과 같은 speech rate 제어가 가능

$p,q$에 대한 $m(\cdot)$의 관계, $p,q$는 각각 input/output sequence의 index

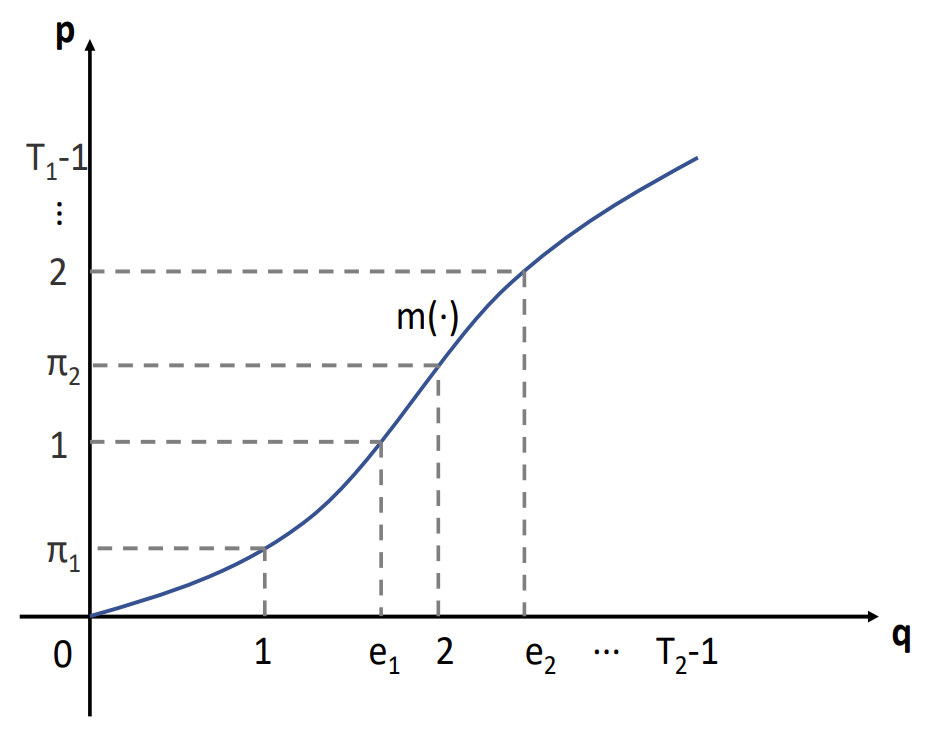
- Aligned Reconstruction

• Hidden representation $h$를 time-aligned representation에 mapping 하기 위해서는 학습과 추론 모두에서 alignment matrix가 필요함
  • 이때 IMV $\pi$나 aligned position $e$로부터 alignment를 구성할 수 있음
    - (Eq. 11)은 $\pi$로부터 alignment matrix를 효과적으로 reconstruction 할 수 있지만, 추론 중에는 $\pi$대신 aligned position $e$를 사용해야 하기 때문
    - 따라서 학습과 추론의 consistency를 위해 aligned position $e$에서 aligned matrix를 reconstruct 해야 함
  • 이를 위해 학습 과정에서는 (Eq. 18)에서 계산된 aligned position $e$를 사용하고, 추론 시에는 aligned position predictor에서 예측된 position을 사용
    1. 따라서 aligned position $e$로 centered 된 Gaussian kernel을 도입하여 alignment matrix $\alpha'$을 reconstruct 하면:
       (Eq. 20) $\alpha'_{i,j}= \frac{\exp(-\sigma^{-2}(e_{i}-q_{j})^{2})}{\sum_{m=0}^{T_{1}-1}\exp (-\sigma^{-2}(e_{m}-q_{j})^{2})}$
       - $q$ : output sequence의 index vector
    2. 이때 output sequence length $T_{2}$는 학습 시에서는 알려져 있고, 추론 시에는 $e$로부터 계산됨:
       (Eq. 21) $T_{2}= e_{T_{1}-1}+\eta*\Delta e_{T_{1}-1}$
       - $\eta$ : hyperparameter (논문에서는 1.2로 설정)
  • 이렇게 reconsturct 된 alignment는 $e$의 low-resolution으로 인해 (Eq. 11)로 계산된 것만큼 accurate하지는 않음
    - BUT, network를 통해 compensate 될 수 있을 만큼 output에 미치는 영향은 적음
    - 결과적으로 학습/추론 과정에서 consistency가 향상되어 음성 품질을 향상할 수 있음
  • 최종적으로 EfficientTTS는
    - (Eq. 1)에 따라 $\alpha'$을 사용하여 text-encoder output $h$를 time-aligned representation으로 mapping 한 다음,
    - Time-aligned representation이 decoder의 input으로 전달됨 

- Decoder

• Decoder의 input/output은 모두 time-aligned 되어 있으므로 parallel structure decoder를 구성할 수 있음
  • EFTS-CNN
    - Convolution stack을 통해 decoder를 parameterize 함
    - Mean Squared Error (MSE)를 reconstruction loss로 사용
  • EFTS-Flow
    - TTS 모델이 생성된 음성의 variation을 제어할 수 있도록 flow-based decoder를 활용
    - 학습 단계에서는, likelihood를 최대화하여 mel-spectrogram에서 Gaussian 분포 $\mathcal{N}(0,I)$로의 transformation $f$를 학습
    - 추론 단계에서는, Gaussian 분포 $\mathcal{N}(0,I)$에서 latent variabel $z$를 sampling 하고 temperature factor $t$를 통해 zero vector $o$를 $z$로 interpret 하여 새로운 latent vector $z'$을 얻음
    - 결과적으로 $z'$을 input으로 사용하고 transformation $f$를 inverse 하여 mel-spectrogram을 생성
    - 구조적으로는 Flow-TTS의 decoder를 활용
  • EFTS-Wav
    - TTS 모델을 end-to-end 방식으로 학습하기 위해 EfficientTTS와 dilated convolutional adversarial decoder를 결합
    - 구조적으로는 MelGAN을 활용

Decoder에 따른 EfficientTTS 변형 구조들 (좌) EFTS-Flow (중) EFTS-CNN (우) EFTS-Wav

3. Experiments

- Settings

• Dataset : DataBaker, LJSpeech
• Comparisons : Glow-TTS, Tacotron2

- Results

• Speech Quality
  • MOS 측면에서 DataBaker dataset에 대한 합성 품질을 평가
    - 결과적으로 EfficientTTS의 합성 품질이 가장 우수한 것으로 나타남
    - Tacotron2의 낮은 품질은 teacher forcing training과 autoregressive 추론 간의 inconsistency 때문
    - Glow-TTS은 hidden representation의 continuity를 corrupt 하는 text sequence의 hidden representation을 replicate 하기 때문
  • EfficientTTS는 token duration보다 expressive 한 IMV를 사용하여 alignment를 reconstruct 하기 때문에 더 나은 품질을 얻을 수 있음

DataBaker dataset에서의 합성 품질 비교

• 마찬가지로 LJSpeech dataset에 대해서도 EfficientTTS가 가장 우수한 합성 품질을 보임
  

LJSpeech dataset에서의 합성 품질 비교

• Training and Inference Speed
  • 추론, 학습 속도 측면에서도 EfficientTTS는 가장 효율적인 것으로 나타남
  • 특히 EFTS-CNN의 경우 추론 latency가 8ms로 Tacotron2 보다 97.5배 빠름

학습, 추론 속도 비교

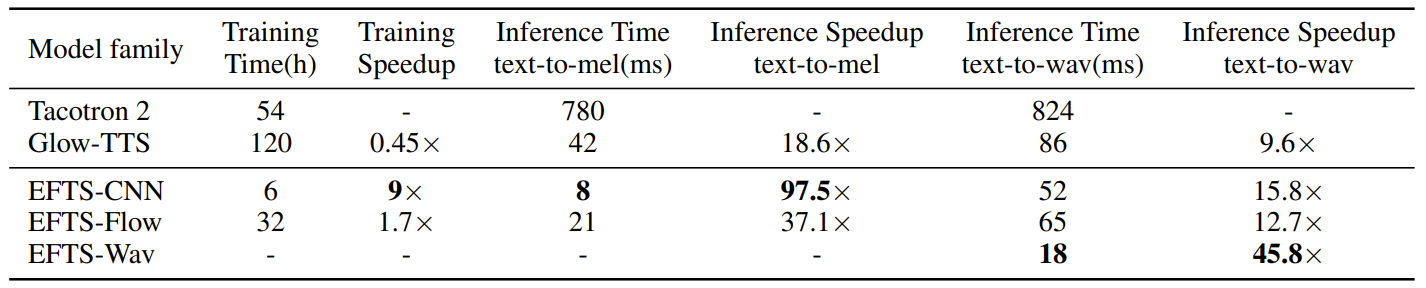
• Monotonic Alignment의 효과를 알아보기 위해 EFTS-CNN에 대한 실험을 수행
  • Variations
    - EFTS-HMA : hard monotonic IMV generator를 사용하는 기본 EFTS-CNN
    - EFTS-SMA : soft monotonic IMV generator를 사용하는 EFTS-CNN
    - EFTS-NM : monotonicity constraint를 사용하지 않는 EFTS-CNN
  • 각 variation들에 대한 학습 결과를 비교해 보면,
    - EFTS-HMA는 EFTS-SMA에 비해 상당한 학습 가속 효과가 있음
    - EFTS-NM은 monotonicity를 학습하지 못해 전혀 수렴되지 않음

EFTS-CNN variation에 대한 학습 결과 비교

• EFTS-CNN variation들의 IMV와 mel-spectrogram을 비교해보면,
  
  • Monotonicity를 고려하지 않는 EFTS-NM에 비해 EFTS-HMA, EFTS-SMA는 alignment를 학습할 수 있음
  • 특히 hard monotonicity를 고려하는 EFTS-HMA의 성능이 가장 우수함
  • 결과적으로 monotonic alignment를 합성 품질 향상에 중요

EFTS-CNN variation에 대한 IMV,&nbsp; Mel-spectrogram 비교

• EfficientTTS의 attention error 발생을 분석해 보면
  
  • Word reapeating, Word skipping, Mispronunciation은 TTS 모델의 대표적인 attention error 
  • EfficientTTS는 Tacotron2에 비해 더 적은 attention error가 발생함
  • 특히 SMA, HMA를 Tacotron2에 적용하면, 기존 Tacotron2 보다 더 적은 attention error가 발생하는 것으로 나타남
    - Monotonic alignment가 TTS 모델의 robustness를 향상하기 때문

Attention error 발생 빈도 비교