[Paper 리뷰] FastVoiceGrad: One-Step Diffusion-based Voice Conversion with Adversarial Conditional Diffusion Distillation

FastVoiceGrad: One-Step Diffusion-based Voice Conversion with Adversarial Conditional Diffusion Distillation

---

• Diffusion-based Voice Conversion은 multi-step reverse diffusion으로 인해 추론 속도가 느림
• FastVoiceGrad
  • 기존 voice conversion model의 성능을 유지하면서 multi-step iteration을 one-step으로 reduce
  • 이를 위해 Adversarial Conditional Diffusion Distillation을 도입하고 sampling 시 initial state를 reconsidering
• 논문 (INTERSPEECH 2024) : Paper Link

---

1. Introduction

• Voice Conversion (VC)는 linguistic content를 change 하지 않으면서 voice를 convert 하는 것을 목표로 함
  • 이때 parallel corpus를 collect 하기 어려우므로 parallel corpus 없이 mapping을 학습할 수 있는 non-parallel VC model이 주로 활용됨
    - 이를 위해 Variation AutoEncoder (VAE), Generative Adversarial Network (GAN), Flow, Diffusion 등의 generative method를 고려할 수 있음
  • 특히 DiffVC와 같이 diffusion-based VC model을 사용하면 우수한 conversion 성능을 달성할 수 있음
    - BUT, diffusion-based VC model은 noise에서 mel-spectrogram과 같은 acoustic feature로 transform 하기 위해 iterative reverse process가 필요하므로 느린 추론 속도의 문제가 있음

One-Step Voice Conversion

-> 그래서 diffusion-based VC model의 추론 속도를 개선한 FastVoiceGrad를 제안

 

• FastVoiceGrad
  • One-step conversion을 위해 Adversarial Conditional Diffusion Distillation (ACDD)를 도입
    - Multi-step teacher diffusion model을 one-step student diffusion model로 distill 함
  • 추가적으로 sampling에서 initial state를 reconsider 하여 VC를 위한 optimal configuration을 explore 

< Overall of FastVoiceGrad >

• ACDD를 활용하여 추론 속도 문제를 해결한 one-step diffusion-based VC model
• 결과적으로 기존보다 빠른 추론 속도와 우수한 covnersion 성능을 달성

2. Preliminary: VoiceGrad

• VoiceGrad는 Denoising Score Matching (DSM)과 Denoising Diffusion Probabilistic Model (DDPM)을 모두 고려하지만, 논문에서는 우수한 VC 성능을 보이는 DDPM-based model에 focus 함
  - 추가적으로 any-to-any VC를 지원하기 위해 speaker encoder를 사용하여 speaker embedding을 추출함

- Overview

• DDPM은 data-to-noise (diffusion) process를 gradual noising process $\mathbf{x}_{0}\rightarrow \mathbf{x}_{1}\rightarrow ...\rightarrow \mathbf{x}_{T}$로 represent 함
  • 여기서 $T=1000$은 step 수, $\mathbf{x}_{0}$는 real data, $\mathbf{x}_{T}$는 $\mathbf{x}_{T}\sim \mathcal{N}(0,I)$의 noise를 의미함
  • Noise-to-data (reverse diffusion) process의 경우, neural network를 통해 $\mathbf{x}_{T}\rightarrow \mathbf{x}_{T-1}\rightarrow ...\rightarrow \mathbf{x}_{0}$과 같이 gradual denoising을 수행함
  • 결과적으로 diffusion process는 다음과 같이 정의됨:
    1. Markov chain을 가정했을 때 one-step diffusion process $q(\mathbf{x}_{t}|\mathbf{x}_{t-1}), \,\, t\in \{1,...,T\}$는:
       (Eq. 1) $ q(\mathbf{x}_{t}|\mathbf{x}_{t-1})=\mathcal{N}(\mathbf{x}_{t};\sqrt{\alpha_{t}}\mathbf{x}_{t-1} ,\beta_{t}I)$
       - $\alpha_{t}=1-\beta_{t}$
    2. Normal distribution의 reproductivity를 통해 $q(\mathbf{x}_{t}|\mathbf{x}_{0})$는 analytically obtain 됨:
       (Eq. 2) $q(\mathbf{x}_{t}|\mathbf{x}_{0})=\mathcal{N}(\mathbf{x}_{t};\sqrt{\bar{\alpha}_{t}}\mathbf{x}_{0} ,(1-\bar{\alpha}_{t})I)$
       - $\bar{\alpha}_{t}=\prod_{i=1}^{t}\alpha_{i}$
    3. Reparameterization trick을 적용해 (Eq. 2)를 rewrite 하면:
       (Eq. 3) $\mathbf{x}_{t}=\sqrt{\bar{\alpha}_{t}}\mathbf{x}_{0}+\sqrt{1-\bar{\alpha}_{t}}\epsilon$
       - $\epsilon\sim \mathcal{N}(0,I)$, $\beta_{t}$는 pre-determined noise schedule에 따라 constant value로 fix 됨
  • Reverse diffusion process는:
    1. One-step reverse diffusion process $p_{\theta}(\mathbf{x}_{t-1}|\mathbf{x}_{t})$는 다음과 같이 정의됨:
       (Eq. 4) $p_{\theta}(\mathbf{x}_{t-1}|\mathbf{x}_{t})=\mathcal{N}(\mathbf{x}_{t-1};\mu_{\theta} (\mathbf{x}_{t},t,\mathbf{s},\mathbf{p}),\sigma^{2}_{t}I)$
       - $\mu_{\theta}$ : $\theta$로 parameterize 된 model의 output으로, $t$, speaker embedding $\mathbf{s}$, phoneme embedding $\mathbf{p}$로 condition 됨
       - $\sigma_{t}^{2}=\frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_{t}}\beta_{t}$
    2. $\mathbf{x}_{0},\mathbf{s},\mathbf{p}$는 동일한 waveform에서 추출되고, reparameterization trick을 적용하면 (Eq. 4)를 다음과 같이 rewrite 할 수 있음:
       (Eq. 5) $\mathbf{x}_{t-1}=\mu_{\theta}(\mathbf{x}_{t},t,\mathbf{s},\mathbf{p})+\sigma_{t}\mathbf{z}$
       - $\mathbf{z}\sim\mathcal{N}(0,I)$

- Training Process

• DDPM의 training objective는 negative log-likelihood의 variational bound $\mathbb{E}[-\log p_{\theta}(\mathbf{x}_{0})]$를 minimize 하는 것과 같음
  • 수식적으로:
    (Eq. 6) $\mathcal{L}_{DDPM}(\theta)=\mathbb{E}_{q(\mathbf{x}_{1:T}|\mathbf{x}_{0})} \left[-\log \frac{p_{\theta}(\mathbf{x}_{0:T})}{q(\mathbf{x}_{1:T}|\mathbf{x}_{0})}\right]$
  • (Eq. 3)을 따라 reparameterization을 적용하면:
    (Eq. 7) $\mu_{\theta}(\mathbf{x}_{t},t,\mathbf{s},\mathbf{p})=\frac{1}{\sqrt{\alpha_{t}}}\left( \mathbf{x}_{t}-\frac{1-\alpha_{t}}{\sqrt{1-\bar{\alpha}_{t}}}\epsilon_{\theta} (\mathbf{x}_{t},t,\mathbf{s},\mathbf{p})\right)$
    
  • (Eq. 6)은 다음과 같이 rewrite 할 수 있음:
    (Eq. 8) $\mathcal{L}_{DDPM}(\theta)=\sum_{t=1}^{T}w_{t}\mathbb{E}_{\mathbf{x}_{0},\epsilon} \left[\left|\left| \epsilon-\epsilon_{\theta}(\mathbf{x}_{t},t,\mathbf{s},\mathbf{p})\right|\right|_{1}\right]$
    - $\epsilon_{\theta}$ : $\mathbf{x}_{t},t,\mathbf{s},\mathbf{p}$를 사용하여 $\epsilon$을 predict 하는 noise predictor
    - $w_{t}=1$ : constant
  • 기존 DDPM에서는 $L2$ loss를 사용하지만 논문은 WaveGrad를 따라 $L1$를 사용함

- Conversion Process

• $\epsilon_{\theta}$가 training 되면 VoiceGrad는 주어진 source mel-spectrogram $\mathbf{x}_{0}^{src}$를 [Algorithm 1]을 통해 target mel-spectrogram $\mathbf{x}_{0}^{tgt}$으로 convert 함
  • [Algorithm 1]에서 target speaker embedding $\mathbf{s}^{tgt}$과 source phoneme embedding $\mathbf{p}^{src}$는 auxiliary information으로 사용됨
    1. 이때 sampling을 accelerate 하기 위해, 논문은 subsequence $\{S_{K},...,S_{1}\}$를 $\{T,...,1\}$ 대신 $t$ value의 sequence로 사용함
       - $K\leq T$
    2. 이를 기반으로 $\alpha S_{k}$는 $k>1$일 때 $\alpha S_{k}=\frac{\bar{\alpha}S_{k}}{\bar{\alpha}S_{k-1}}$로, $k=1$일 때 $\alpha S_{k}=\bar{\alpha} S_{k}$로 redefine 됨
       - $\sigma_{S_{k}}$도 마찬가지로 modify 됨
  • VC task는 generation task가 아니므로, generation task에서 사용되는 random noise $\mathbf{x}_{T}\sim \mathcal{N}(0,I)$ 대신 $\mathbf{x}_{0}^{src}$가 $\mathbf{x}$의 initial value로 사용됨
    - 마찬가지로 $t$의 initial value는 $T$에서 $S_{K}<T$로 adjust 되어 midterm state에서 reverse diffusion process를 수행함 

Conversion Process

3. FastVoiceGrad

- Rethinking Initial States in Sampling

• [Algorithm 1]에서 source speech의 inheritance에 affect 하는 crucial factor는 $\mathbf{x}, t$의 initial value임
• Rethinking the Initial Value of $\mathbf{x}$
  • $\mathbf{x}$의 initial value가 $\mathbf{x}\sim \mathcal{N}(0,I)$로 설정되면, training-inference gap이 발생하지 않는 대신, content를 preserve 하는 source information $\mathbf{x}_{0}^{src}$를 inherit할 수 없음
    - 반대로 $\mathbf{x}_{0}^{src}$를 initial value로 directly use 하면, source information을 inherit 할 수 있는 대신 training-inference gap이 발생함
  • 이를 고려하여 논문은 diffused source mel-spectrogram $\mathbf{x}_{S_{K}}^{src}$를 사용함:
    (Eq. 9) $\mathbf{x}_{S_{K}}^{src}=\sqrt{\bar{\alpha}_{S_{K}}}\mathbf{x}_{0}^{src} +\sqrt{1-\bar{\alpha}_{S_{K}}}\epsilon$
    
• Rethinking the Initial Value of $t$ ($S_{K}$)
  • $S_{K}$가 $T$에 close 할 수록 $\mathbf{x}$는 더 많은 noise를 포함하게 되므로, essential information을 corrupt 할 수 있음
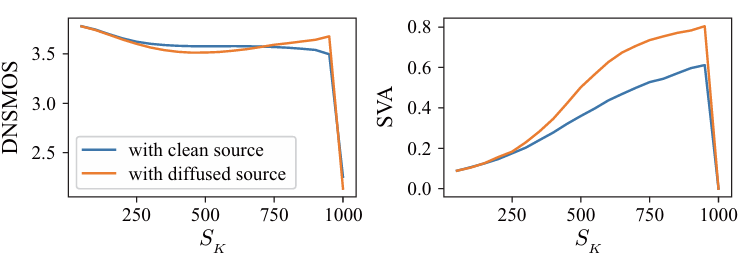
  • 실제로 아래 그림과 같이 $S_{K}$와 DNSMOS, Speaker Verification Accuracy (SVA)를 비교해 보면:
    1. SVA는 $S_{K}$가 증가함에 따라 지속적으로 개선됨
       - $\mathbf{x}$가 target speaker로 largely transform 되기 때문
    2. 반면 DNSMOS는 $S_{K}$가 증가함에 따라 저하됨
    3. 이때 $\mathbf{x}$의 initial value로 $\mathbf{x}_{S_{K}}^{src}$를 사용하는 경우, DNSMOS의 지속적인 저하를 방지할 수 있음
       - $S_{K}$가 증가함에 따라 diffusion process를 통해 training-inference 간의 gap이 alleviate 되기 때문
  • 한편으로 $S_{K}=1000$일 때 DNSMOS, SVA 모두 상당한 감소가 발생함
    - 이는 one-step generation 시 $\mathbf{x}$에 source information이 small amount라도 포함되어 있어야 한다는 것을 의미함
  • 해당 결과를 기반으로 논문은 $S_{K}=950$의 $\mathbf{x}_{S_{K}}^{src}$를 채택함

$S_{K}$와 DNSMOS, SVA 간의 관계

- Adversarial Conditional Diffusion Distillation

• One-step diffusion model을 scratch로 training 하는 것은 어려우므로, 논문은 pre-trained VoiceGrad를 initial model로 사용하고, ACDD를 적용하여 one-step model을 얻음
  - Distillation 시에는 adversarial loss와 score distillation loss가 적용됨
• Adversarial loss
  • MaskCycleGAN-VC, StarGANv2-VC와 같이 mel-spectrogram에 discriminator를 directly apply 할 때, buzzy sound를 eliminate 하는 optimal discriminator를 결정하는 것은 어려움
    - 따라서 논문은 mel-spectrogram을 frozen parameter를 가진 neural vocoder $\mathcal{V}$를 사용하여 waveform으로 변환한 다음, waveform domain에서 discriminator $\mathcal{D}$를 적용함
  • 이때 adversarial loss는 다음과 같음:
    (Eq. 10) $\mathcal{L}_{adv}(\mathcal{D})=\mathbb{E}_{\mathbf{x}_{0}}\left[ (\mathcal{D}(\mathcal{V}(\mathbf{x}_{0}))-1)^{2}+(\mathcal{D}(\mathcal{V}(\mathbf{x}_{\theta})))^{2}\right]$
    (Eq. 11) $\mathcal{L}_{adv}(\theta)=\mathbb{E}_{\mathbf{x}_{\theta}}\left[ (\mathcal{D}(\mathcal{V}(\mathbf{x}_{\theta}))-1)^{2}\right]$
    - $\mathbf{x}_{0}$ : real speech에서 추출된 mel-spectrogram
    - $\mathbf{x}_{\theta}$ : (Eq. 7)의 one-step denoising prediction $\mathbf{x}_{\theta}=\mu_{\theta}(\mathbf{x}_{S_{k}},S_{K},\mathbf{s},\mathbf{p})$를 통해 얻어지는 mel-spectrogram
    - $\mathbf{x}_{S_{k}}$ : (Eq. 9)를 통해 얻어지는 $S_{K}$-step diffusion $\mathbf{x}_{0}$
    - 해당 adversarial loss는 adversarial training에서 $\mathbf{x}_{\theta}$의 reality를 향상하기 위해 사용됨
  • 추가적으로 neural vocoder training을 따라, Feature Matching (FM) loss를 적용함:
    (Eq. 12) $\mathcal{L}_{FM}(\theta)=\mathbb{E}_{\mathbf{x}_{0}}\left[ \sum_{l=1}^{L}\frac{1}{N_{l}}\left|\left| \mathcal{D}_{l}(\mathcal{V}(\mathbf{x}_{0})) - \mathcal{D}_{l}(\mathcal{V}(\mathbf{x}_{\theta}))\right|\right|_{1}\right]$
    - $L$ : $\mathcal{D}$의 layer 수, $\mathcal{D}_{l},N_{l}$ : $\mathcal{D}$의 $l$-th layer의 feature, feature 수
    - $\mathcal{L}_{FM}(\theta)$는 discriminator space에서 $\mathbf{x}_{\theta}$가 $\mathbf{x}_{0}$와 close 하도록 함
• Score Distillation loss
  • Score distillation loss는 다음과 같이 formulate 됨:
    (Eq. 13) $\mathcal{L}_{dist}(\theta)=\mathbb{E}_{t,\mathbf{x}_{0}}\left[c(t)||\mathbf{x}_{\phi}- \mathbf{x}_{\theta}||_{1}\right]$
  • $\mathbf{x}_{\phi}$는 $\phi$로 parameterize 된 teacher diffusion model을 통해 얻어진 (Eq. 7)의 one-step denoising prediction으로써, $\mathbf{x}_{\phi}=\mu_{\phi}(\text{sg}(\mathbf{x}_{\theta,t}),t,\mathbf{s},\mathbf{p})$에 해당함
    - $\text{sg}$ : stop-gradient operation, $\mathbf{x}_{\theta,t}$ : (Eq. 3)의 $t$-step diffused $\mathbf{x}_{\theta}$, $t\in \{1,...,T\}$
    - $c(t)$ : weighting term으로써 $\alpha_{t}$로 설정됨
  • $\mathcal{L}_{dist}(\theta)$는 student output $\mathbf{x}_{\theta}$가 teacher output $\mathbf{x}_{\phi}$에 match 되도록 함
• Total loss
  • 결과적으로 얻어지는 total loss는:
    (Eq. 14) $\mathcal{L}_{ACDD}(\theta)=\mathcal{L}_{adv}(\theta)+\lambda_{FM}\mathcal{L}_{FM}(\theta) +\lambda_{dist}\mathcal{L}_{dist}(\theta)$
    (Eq. 15) $\mathcal{L}_{ACDD}(\mathcal{D})=\mathcal{L}_{adv}(\mathcal{D})$
    - $\lambda_{FM}=2, \lambda_{dist}=45$ : weighting hyperparameter
    
  • $\theta, \mathcal{D}$는 각각 $\mathcal{L}_{ACDD}(\theta), \mathcal{L}_{ACDD}(\mathcal{D})$를 minimize 하여 optimize 됨 

4. Experiments

- Settings

• Dataset : VCTK
• Comparisons : DiffVC, VoiceGrad

- Results

• 전체적으로 FastVoiceGrad의 성능이 가장 뛰어남

VCTK에서의 성능

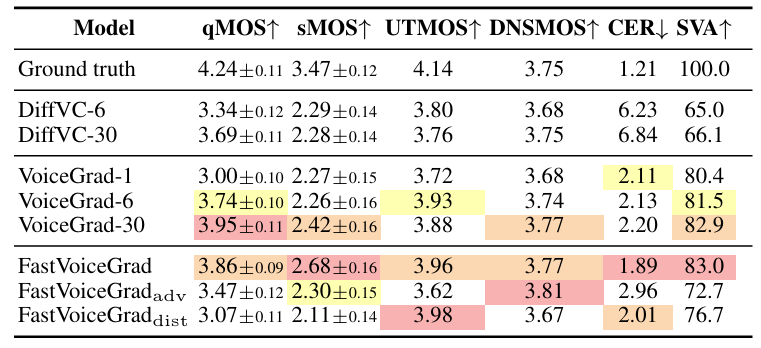
• LibriTTS에 대해서도 우수한 성능을 보임

LibriTTS에서의 성능