[Paper 리뷰] LinearVC: Linear Transformations of Self-Supervised Features through the Lens of Voice Conversion

LinearVC: Linear Transformations of Self-Supervised Features through the Lens of Voice Conversion

---

• Self-supervised representation을 활용하여 voice conversion method를 구성할 수 있음
• LinearVC
  • Self-supervised feature에 대한 simple linear transformation을 통해 voice를 converting
  • Allowed transformation set을 constraining 하고 singular value decomposition을 통해 content, speaker information을 explicitly factorize
• 논문 (INTERSPEECH 2025) : Paper Link

---

1. Introduction

• Voice Conversion (VC)는 input speech를 target speaker voice로 altering 하는 것을 목표로 함
  • 이를 위해서는 phonetic information과 speaker identity information을 disentangle 해야 함
    
    1. 대표적으로 SoundStorm은 VC task를 위해 large spoken language model을 활용하고 StreamVC는 speaker embedding을 conditioning signal로 사용함
    2. 한편으로 FragmentVC, kNN-VC 등과 같이 Self-Supervised Learning (SSL) representation을 활용할 수도 있음
  • BUT, 대부분의 방식은 SSL model이 content, speaker information을 어떻게 organize 하는지 신경쓰지 않음

-> 그래서 SSL feature에 대한 insight를 기반으로 VC task를 수행하는 LinearVC를 제안

 

• LinearVC
  • WavLM의 intermediate layer feature를 기반으로 source, target frame 간의 linear projection을 학습
    1. 추론 시에는 source speech를 linearly project하고 pre-trained vocoder를 통해 waveform을 생성
    2. 특히 kNN-VC의 non-linear nearest neighbour mapping을 linear transformation으로 replace
  • 추가적으로 singular value decomposition을 활용해 content, speaker information을 explicitly factorize

< Overall of LinearVC >

• SSL feature에 linear transformation을 적용한 VC model
• 결과적으로 기존보다 우수한 VC 성능을 달성

2. Method

• LinearVC는 training 중에 source에서 target speaker로의 linear transformation을 학습함
  • 먼저 utterance는 WavLM과 같은 large SSL speech model을 사용하여 $D$-dimensional feature frame으로 encoding 됨
    1. 이후 $N$ source frame에 대해 $M$ target frame에서 closest neighbour를 find 함
    2. 여기서 source frame은 matrix $\mathbf{X}\in\mathbb{R}^{N\times D}$에 arrange 되고 target frame은 matrix $\mathbf{Y}\in\mathbb{R}^{N\times D}$에 arrange 됨 
  • 그러면 multivariate linear regression을 solve 하여 projection matrix $\mathbf{W}$를 find 할 수 있음:
    (Eq. 1) $\arg\min_{\mathbf{W}}\left|\left| \mathbf{Y}-\mathbf{XW}\right|\right|_{F}^{2}$
    - $||\cdot||_{F}$ : Frobenius norm
  • 추론 시 source utterance $\mathbf{X}_{src}$의 각 frame은 linearly project 되어 converted output $\mathbf{X}_{tgt}=\mathbf{X}_{src}\mathbf{W}$를 얻음
    - Pre-trained HiFi-GAN vocoder는 projected frame으로부터 final speech waveform을 생성함
  • 논문은 phonetic information이 모든 speaker에 대해 SSL space 내에서 structured 되어 있다는 것에 기반함
    - 즉, 해당 phonetic subspace가 존재한다면 space 내의 서로 다른 location으로 project 했을 때, content는 maintain 하면서 voice characteristic은 altering 되어야 함

Overview

3. Experiments

- Settings

• Dataset : LibriSpeech
• Comparisons : kNN-VC, FreeVC, SoundStorm

- Results

• 전체적으로 LinearVC의 성능이 가장 우수함

Model 성능 비교

• Constrained Linear Transformations
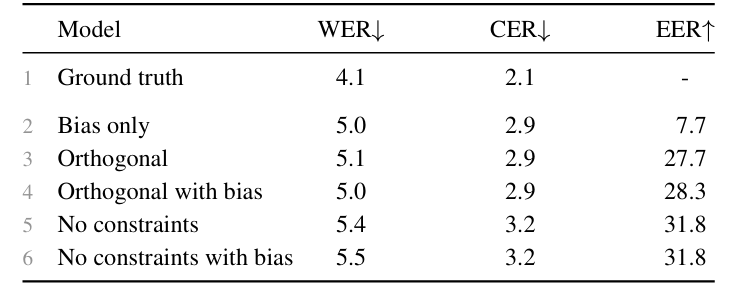
  • 아래 그림과 같이 bias vector, $\mathbf{W}$에 대한 orthogonal constraint, no constraint의 3가지 transformation을 고려하자

Linear Transformation

• 이때 transformation에 관계없이 intelligibility (W/CER)는 maintain 되고, rotation과 reflection이 가능한 경우 speaker similarity (EER)이 크게 향상됨

Linear Transformation 별 성능

• 아래 그림과 같이 matrix estimation을 위해 동일한 speaker의 서로 다른 sample (상단)을 사용하는 경우와 서로 다른 speaker pair (하단)를 사용하는 경우를 비교해 보면
  • Linear transformation은 sample에 관계없이 dimension $35$와 $148$을 modify 함
  • 해당 modification은 speaker subspace 내에서의 움직임을 의미함

Projection Matrix

4. Factorizing Out a Shared Content Subspace

• 앞선 결과는 content information은 low-dimensional subspace에 embed 되어 있고, linear transformation을 통해 target voice를 생성할 수 있다는 것을 의미함
  - 추가적으로 논문은 SSL feature를 모든 speaker에 대해 share 되는 content representation과 speaker-specific transformation set으로 factorize 하여 위의 결과를 validate 함

- LinearVC with Content Factorization

• 먼저 $K$ distinct speaker에 대한 self-supervised feature를 추출함
  • 이후 single source speaker를 choice 하고 다른 speaker에 대해 nearest neighbour를 사용하여 matching feature vector를 find 함
    - 해당 feature를 각각의 speaker에 대해 하나씩, matrix $\mathbf{X}_{k}\in \mathbb{R}^{N\times D}$로 arrange 함
  • 그런 다음 optimization problem을 solve 하여 $\mathbf{X}_{1},...,\mathbf{X}_{k}$를 shared content representation $\mathbf{C}$와 speaker-specific transformation $\mathbf{S}_{k}$로 factorize 함:
    (Eq. 2) $\min_{\mathbf{C},\mathbf{S}_{k}}\sum_{k=1}^{K}\left|\left| \mathbf{X}_{k}-\mathbf{CS}_{k}\right|\right|_{F}^{2},\,\,\, \text{subject to}\,\,\, \text{rank}\left(\mathbf{CS}_{k}\right)\leq r$
    - $r$ : factorization의 rank를 constraining 하는 hyperparameter
  • Feature dimension을 따라 $\mathbf{X}_{k}$를 concatenate 하여 (Eq. 2)를 rewrite 하면:
    (Eq. 3) $\min_{\mathbf{C},\mathbf{S}}\left|\left|\mathbf{X}-\mathbf{CS}\right|\right|_{F}^{2}, \,\,\, \text{subject to}\,\,\, \text{rank}(\mathbf{CS})\leq r$
    - $\mathbf{X}\in \mathbb{R}^{N\times KD}, \mathbf{S}\in\mathbb{R}^{r\times KD}$ : resulting block matrix
  • (Eq. 3)은 block matrix $\mathbf{X}$의 Singular Value Decomposition을 통해 solve 할 수 있음
    1. 특히 논문은 $\mathbf{X}_{k}$를 $\mathbf{U\Sigma S}_{k}$로 approximate 함
       - $\mathbf{U}\in\mathbb{R}^{N\times r}$ : orthogonal matrix
       - $\mathbf{\Sigma}\in\mathbb{R}^{r\times r}$ : $r$ largest singular value의 diagonal matrix
       - $\mathbf{S}_{k}\in \mathbb{R}^{r\times D}$ : $\mathbf{X}$의 right-singular vector
    2. Product $\mathbf{U\Sigma}$는 shared content $\mathbf{C}$를 represent 하고, 각 $\mathbf{S}_{k}$는 speaker-specific linear transformation에 해당함
  • 해당 factorization을 기반으로 conversion을 수행하기 위해, 논문은 source utterance $\mathbf{X}_{src}$를 content subspace에 project 한 다음 target speaker transformation을 적용함
    1. 이때 $\mathbf{X}_{src}\approx \mathbf{CS}_{src}$이므로 source speaker transformation $\mathbf{S}_{src}^{+}$의 pseudo-inverse를 multiply 하여 content subspace에 project 할 수 있음:
       (Eq. 4) $\mathbf{X}_{src}\mathbf{S}_{src}^{+}\approx \mathbf{C}$
    2. 이후 target speaker transformation을 적용하여 desired speaker voice로 convert 함:
       (Eq. 5) $\mathbf{X}_{tgt}=\mathbf{X}_{src}\mathbf{S}_{src}^{+}\mathbf{S}_{tgt}$
       - $\mathbf{S}_{src}^{+}\mathbf{S}_{tgt}$은 non-factorized LinearVC의 projection matrix $\mathbf{W}$와 같이 동작하지만, transformation rank $r$을 explicitly setting 할 수 있음

• Voice Conversion Results
  • 먼저 $24$ rank를 사용하는 경우 최적의 CER을 달성할 수 있음
    - 이는 content information이 low dimension의 subspace에 존재한다는 것을 의미함
  • EER의 경우 $100$ 이상의 large rank가 필요함
    - 이는 speaker transformation이 많은 parameter를 요구한다는 것을 의미함
  • 결과적으로 LinearVC는 해당 decomposition을 통해 speaker, content information을 disentangle 함

Content Factorization을 사용했을 때 Intelligibility, Speaker Similarity