[Paper 리뷰] NaturalSpeech2: Latent Diffusion Models are Natural and Zero-Shot Speech and Singing Synthesizers

NaturalSpeech2: Latent Diffusion Models are Natural and Zero-Shot Speech and Singing Synthesizers

---

• 기존의 large-scale text-to-speech system은 speech를 discrete token으로 quantize 하고 language model을 기반으로 해당 token을 처리함
  - 따라서 unstable prosody, word skipping/repeating 등의 문제가 발생함
• NaturalSpeech2
  • Quantized latent vector를 얻기 위해 residual vector quantizer에 기반한 neural audio codec을 활용
  • 이후 diffusion model을 활용하여 text input에 condition 된 latent vector를 합성
• 논문 (ICLR 2024) : Paper Link

---

1. Introduction

• Text-to-Speech (TTS)는 NaturalSpeech와 같이 human-like speech를 생성하는 것을 목표로 함
  • BUT, speaker-limited recording-studio dataset에 대한 의존성으로 인해 TTS system은 다양한 speaker identity, prosody, style을 반영하기 어려움
  • 이를 해결하기 위해 large-scale corpus를 활용하거나 unseen scenario에 대한 few-/zero-shot adaptation을 적용할 수 있음
    - 대표적으로 VALL-E, SPEAR-TTS와 같은 large-scale TTS는 continuous speech waveform을 discrete token으로 quantize 한 다음, 해당 token을 autoregressive language model을 통해 처리함
  • BUT, 해당 large-scale TTS는 다음의 한계가 있음:
    1. Discrete speech token sequence는 상당히 길기 때문에 autoregressive model은 error propagation으로 인한 unstable speech output이 발생함
    2. Codec과 language model 간에는 아래 표와 같은 dillemma가 존재함
       - Low bitrate token sequence는 language model에서 활용하기 쉽지만 high-frequency fine-grained acoustic detail에 대한 information loss가 발생함
       - SoundStream, DAC와 같은 residual discrete token은 flatten시 token sequence가 길어지므로 language modeling이 어려움

Audio Codec과 Autoregressive Model 간의 Dilemma

-> 그래서 expressive prosody, robustness, strong zero-shot ability를 만족하는 NaturalSpeech2를 제안

 

• NaturalSpeech2
  • Codec encoder를 사용하여 speech waveform을 latent vector sequence로 변환하고, codec decoder를 통해 해당 latent vector에서 speech waveform을 reconstruct
    - 이때 training set에서 codec encoder를 통해 latent vector를 추출한 다음, phoneme encoder, duration predictor, pitch predictor로 condition 된 latent diffusion model의 target으로 활용
  • 추론 시에는 latent diffusion model을 사용하여 text/phoneme sequence에 대한 latent vector를 생성한 다음, codec decoder를 사용해 latent vector로부터 speech waveform을 생성

< Overall of NaturalSpeech2 >

• Continuous vector와 latent diffusion model을 기반으로 한 zero-shot TTS model
• 결과적으로 기존보다 우수한 합성 성능을 달성

Large-Scale TTS vs NaturalSpeech2

2. Method

• NaturalSpeech2는 다양한 speaker identity, prosody, style을 포함한 high-fidelity/expressive/robust zero-shot speech를 생성하는 것을 목표로 함
  • 구조적으로는 nerual audio codec (Codec Encoder/Decoder), prior (Phoneme Encoder, Duration/Pitch Predictor)가 있는 diffusion model로 구성됨
  • 이때 논문은 regeneration learning을 채택함
    1. 먼저 audio codec encoder를 통해 speech waveform을 latent vector로 변환하고, codec decoder를 통해 latent vector에서 waveform을 reconstruct 함
    2. 이후 diffusion model을 사용하여 text/phoneme input에 condition 된 latent vector를 predict 함

NaturalSpeech2

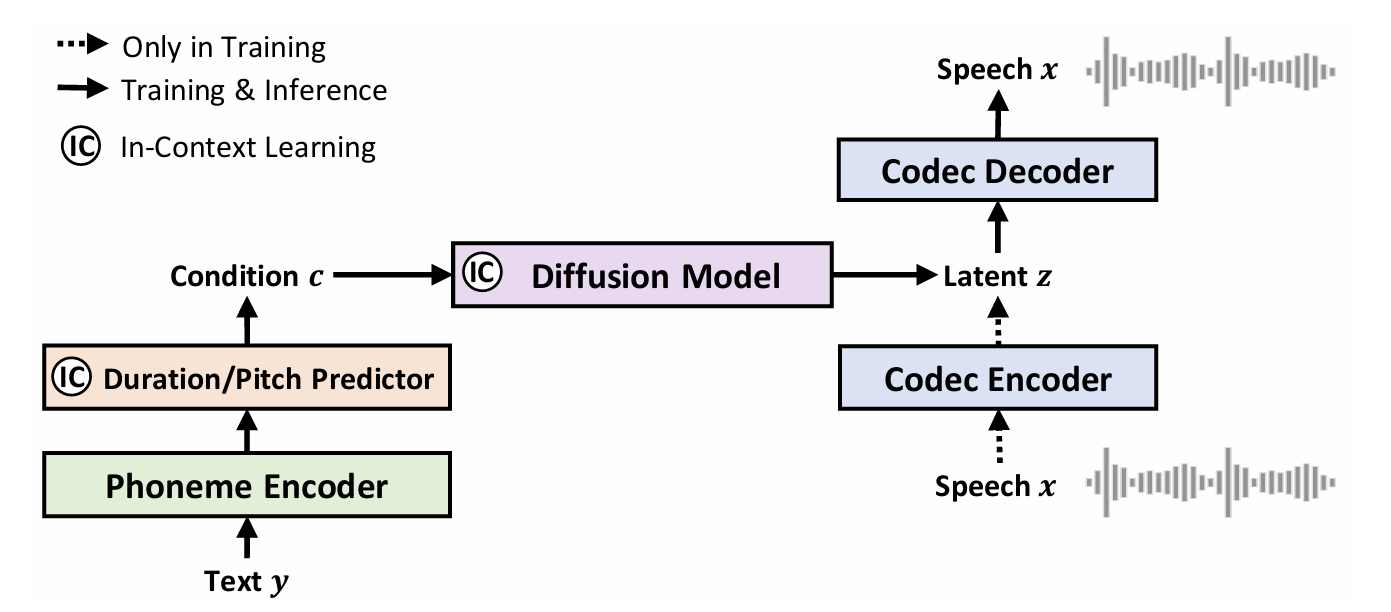
- Neural Audio Codec with Continuous Vectors

• 논문은 neural audio codec을 사용해 speech waveform을 continuous vector로 변환함
  • Continuous vector를 사용하는 audio codec은 다음의 장점을 가짐:
    
    1. Continuous vector는 discrete token보다 lower compression rate를 가지고 higher bitrate를 가지므로 high-quality audio reconstruction을 보장할 수 있음 
    2. Discrete quantization과 달리 각 audio frame에는 하나의 vector만 존재하므로 hidden sequence length가 증가하지 않음 
  • 구조적으로 neural audio codec은 audio encoder, residual vector quantizer (RVQ), audio decoder로 구성됨
    1. Audio encoder는 16kHz audio에 대해 total downsampling rate가 200인 convolution block으로 구성됨
       - 각 frame은 12.5ms speech segment에 해당
    2. RVQ는 SoundStream을 따라 audio encoder output을 multiple residual vector로 변환함
       - 해당 residual vector의 summation은 quantized vector로써, diffusion model의 training target으로 사용됨
    3. Audio decoder는 quantized vector에서 audio waveform을 생성함
    4. 결과적으로 audio neural codec은 다음과 같이 formulate 됨:
       (Eq. 1) $\text{Audio Encoder:}\,\, h=f_{enc}(x),$
       $\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \text{Residual Vector Quantizer:}\,\, \{e_{j}^{i}\}_{j=1}^{R}=f_{rvq}(h^{i}),\,\,z^{i}=\sum_{j=1}^{R}e_{j}^{i},\,\,z=\{z^{i}\}_{i=1}^{n},$
       $\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \text{Audio Decoder:}\,\, x=f_{dec}(z)$
       - $f_{enc},f_{rvq},f_{dec}$ : 각각 audio encoder, RVQ, audio decoder, $x$ : speech waveform
       - $h$ : frame length가 $n$인 audio encoder에서 얻어진 hidden sequence, $z$ : $h$와 같은 length를 가지는 quantized vector sequence
       - $i$ : speech frame index, $j$ : residual quantizer index, $R$ : residual quantizer 수
       - $e_{j}^{i}$ : $i$-th hidden frame (즉, $h^{i}$)에서 $j$-th residual quantizer를 통해 얻어진 codebook ID의 embedding vector
  • 실제로 continuous vector를 얻기 위해서는 vector quantizer 대신 autoencoder나 VAE를 활용해야 함
    - BUT, 논문은 regularization과 efficiency를 위해 매우 많은 quantizer $R$와 codebook token $V$을 가지는 RVQ를 사용하여 continuous vector로 approximate 함
  • 이를 통해 다음의 이점을 얻을 수 있음:
    1. Latent diffusion model training 시 continuous vector를 store 할 필요가 없음
       - 대신 codebook embedding과 quantized token ID를 store 하고 (Eq. 1)을 통해 continuous vector를 derive 함
    2. Continuous vector를 predict 할 때 quantized token ID를 기반으로 하는 discrete classification에 addtional regualarization loss $\mathcal{L}_{ce\text{-}rvq}$를 추가할 수 있음 

Neural Audio Codec

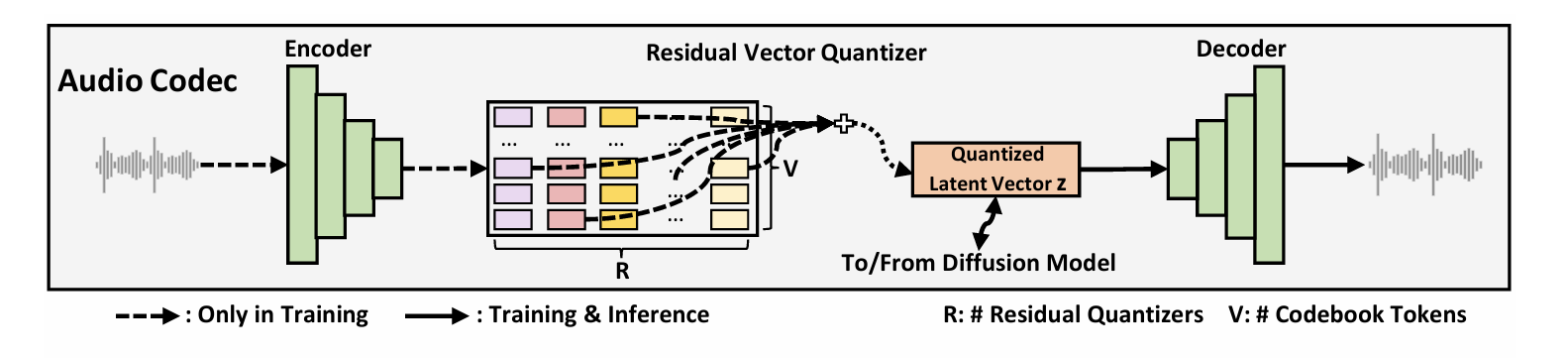
- Latent Diffusion Model with Non-Autoregressive Generation

• 논문은 diffusion model을 활용하여 text sequence $y$에 condition 된 quantized latent vector $z$를 predict 함
  - 구조적으로는 phoneme encoder, duration predictor, pitch predictor로 구성된 prior model을 통해 text input을 처리하고, diffusion model의 condition으로 informative hidden vector $c$를 전달함
• Diffusion Formulation
  • 논문은 diffusion/denoising process를 Stochastic Differential Equation (SDE)를 통해 formulate 함
    1. 먼저 forward SDE는 neural codec에 의해 얻어진 latent vector $z_{0}$를 Gaussian noise로 변환함:
       (Eq. 2) $ \text{d}z_{t}=-\frac{1}{2}\beta_{t}z_{t}\text{d}t+\sqrt{\beta_{t}}\text{d}w_{t},\,\,\,t\in[0,1]$
       - $w_{t}$ : standard Brownian motion, $\beta_{t}$ : non-negative noise schedule function
    2. 그러면 solution은:
       (Eq. 3) $z_{t}=e^{-\frac{1}{2}\int_{0}^{t}\beta_{s}\text{d}s}z_{0}+\int_{0}^{t}\sqrt{\beta_{s}}e^{-\frac{1}{2} \int_{0}^{t}\beta_{u}\text{d}u}\text{d}w_{s}$
    3. Ito Integral에 따라 $z_{0}$이 주어졌을 때 $z_{t}$의 conditional distribution은 Gaussian $p(z_{t}|z_{0})\sim\mathcal{N}(\rho(z_{0},t),\Sigma_{t})$에 해당함
       - $\rho(z_{0},t)=e^{-\frac{1}{2}\int_{0}^{t}\beta_{s}\text{d}s}z_{0}$, $\Sigma_{t}=I-e^{-\int_{0}^{t}\beta_{s}\text{d}s}$
    4. Reverse SDE는 Gaussian noise를 data $z_{0}$로 변환함:
       (Eq. 4) $\text{d}z_{t}=-\left(\frac{1}{2}z_{t}+ \nabla\log p_{t}(z_{t})\right)\beta_{t}\text{d}t+ \sqrt{\beta_{t}}\text{d}\tilde{w}_{t},\,\,\,t\in[0,1]$
       - $\tilde{w}$ : reverse-time Brownian motion 
    5. 추가적으로 reverse process에서 다음의 Ordinary Differential Equation (ODE)를 고려할 수 있음:
       (Eq. 5) $\text{d}z_{t}=-\frac{1}{2}\left(z_{t}+\nabla\log p_{t}(z_{t})\right)\beta_{t}\text{d}t,\,\,\, t\in[0,1]$
  • Noisy data의 log-density gradient에 해당하는 score $\nabla \log p_{t}(z_{t})$를 estimate 하도록 neural network $s_{\theta}$를 training 한 다음, Gaussian noise $z_{1}\sim\mathcal{N}(0,1)$에서 (Eq. 4)/(Eq. 5)를 numerically solve 하여 data $z_{0}$를 sampling 할 수 있음
    - 여기서 neural network $s_{\theta}(z_{t},t,c)$는 WaveNet을 기반으로 하고, noisy vector $z_{t}$, time step $t$, condition information $c$를 input으로 사용하여 data $\hat{z}_{0}$를 predict 함
  • 즉, $\hat{z}_{0}=s_{\theta}(z_{t},t,c)$이고 diffusion model의 loss function은:
    (Eq. 6) $\mathcal{L}_{diff}=\mathbb{E}_{z_{0},t}\left[\left|\left| \hat{z}_{0}-z_{0}\right|\right|_{2}^{2}+ \left|\left| \Sigma_{t}^{-1}\left( \rho(\hat{z}_{0},t) -z-{t}\right)- \nabla\log p_{t}(z_{t})\right|\right|_{2}^{2}+\lambda_{ce\text{-}rvq}\mathcal{L}_{ce\text{-}rvq}\right]$
  • 여기서 first term은 data loss, second term은 score loss에 해당하고, predicted score는 $\Sigma^{-1}_{t}\left(\rho(\hat{z}_{0}^{t},t)-z_{t}\right)$로 얻어짐
    - 해당 score는 추론 시 (Eq. 4) 또는 (Eq. 5)에 기반한 reverse sampling에도 사용됨
  • Third term $\mathcal{L}_{ce\text{-}rvq}$는 RVQ에 대한 cross-entropy (CE) loss에 해당함
    1. 먼저 각 residual quantizer $j\in[1,R]$에 대해 residual vector $\hat{z}_{0}-\sum_{i=1}^{j-1}e_{i}$를 구함
       - $e_{i}$ : $i$-th residual quantizer의 ground-truth quantized embedding
    2. 다음으로 quantizer $j$에서 각 codebook embedding이 있는 residual vector 간의 $L2$ loss를 calculate 하고 softmax function을 통해 probability distribution을 얻음
    3. 이후 ground-truth quantized embedding $e_{j}$와 probability distribution 간의 cross-entropy를 calculate 함
       - 결과적으로 $\mathcal{L}_{ce\text{-}rvq}$는 모든 $R$ residual quantizer의 cross-entropy loss 평균에 해당하고, $\lambda_{ce\text{-}rvq}$는 $0.1$로 설정됨

• Prior Model: Phoneme Encoder and Duration/Pitch Predictor
  • Phoneme encoder는 FastSpeech를 따라 Transformer block으로 구성되고, standard feed-forward network는 phoneme sequence의 local dependency를 capture 하기 위해 convolution network로 변경됨
  • Duration/pitch predictor는 convolution block으로 구성된 동일 structure를 가지지만 서로 다른 parameter를 가짐
    - Ground-truth duration/pitch information은 $L1$ duration loss $\mathcal{L}_{dur}$와 pitch loss $\mathcal{L}_{pitch}$와 함께 learning target으로 사용됨
  • Training 시 ground-truth duration은 frame-level hidden sequence를 얻기 위해 phoneme encoder에서 hidden sequence를 expand 함 
    - 이후 ground-truth pitch information은 frame-level hidden sequence에 add 되어 final condition $c$를 얻음
  • 결과적으로 total loss function은:
    (Eq. 7) $\mathcal{L}=\mathcal{L}_{diff}+\mathcal{L}_{dur}+\mathcal{L}_{pitch}$

Diffusion Model의 WaveNet Architecture

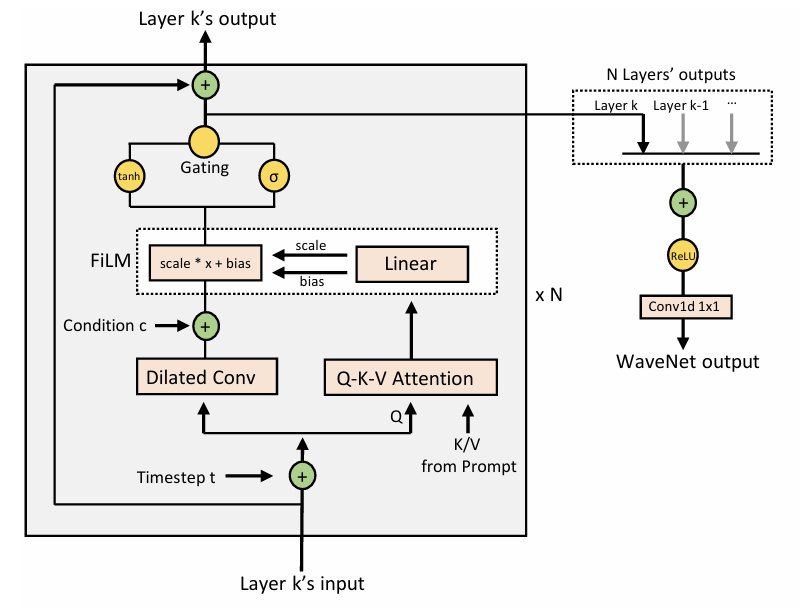
- Speech Prompting for In-Context Learning

• 논문은 in-context learning을 facilitate 하기 위해 duration/pitch predictor와 diffusion model이 speech prompt의 diverse information을 따르도록 하는 speech prompting mechanism을 도입함
  • Speech latent sequence $z$의 경우 frame index가 $u$에서 $v$로 설정된 segment $z^{u:v}$를 randomly cut off 하고,
    1. 나머지 speech segment $z^{1:u},z^{v:n}$을 concatenate 하여 diffusion model의 learning target인 $z^{/u:v}$를 얻음
    2. 이후 Transformer-based prompt encocder를 사용하여 speech prompt $z^{u:v}$ (즉, $z^{p}$)를 처리해 hidden sequence를 얻음
       
  • 이때 해당 hidden sequence를 prompt로 사용하기 위해 다음의 strategy를 적용함:
    1. Duration/pitch encoder의 경우 convolution layer에 Q-K-V attention layer를 insert 함
       - 여기서 query는 convolution layer의 hidden sequence, key/value는 prompt encoder의 hidden sequence
    2. Diffusion model의 경우 2개의 attention block을 도입함
       - First attention block은 $m$ randomly initialized embedding을 query sequence로 prompt hidden sequence에 attend 하여 $m$-length hidden sequence를 얻음
       - Second attention block은 WaveNet layer의 hidden sequence를 query로 사용하고 $m$-length attention result를 key/value로 사용함
  • 추가적으로 second attention block의 attention result를 FiLM layer의 conditional information으로 사용하여 diffusion model에서 WaveNet의 hidden sequence에 대해 affine transformation을 수행함

Speech Prompting

- Connection to NaturalSpeech

• NaturalSpeech2는 이전의 NaturalSpeech와 비교하여 다음의 차이점을 가짐:
  • NaturalSpeech는 LJSpeech와 같은 single-speaker recording-studio dataset에만 focus 하지만 NaturalSpeech2는 large-scale, multi-speaker dataset에 대한 zero-shot ability를 향상하는 것을 목표로 함
  • NaturalSpeech2는 NaturalSpeech의 waveform encoder/decoder, prior module을 그대로 사용하지만 diffusion model, vector quantizer, speech prompting mechanism을 추가로 도입함

3. Experiments

- Settings

• Dataset : MLS, LibriSpeech, VCTK
• Comparisons : YourTTS, VALL-E

- Results

• CMOS 측면에서 NaturalSpeech2가 더 나은 결과를 보임

CMOS 비교

• VALL-E와의 비교에서도 NaturalSpeech2가 더 우수함

NaturalSpeech2 vs VALL-E

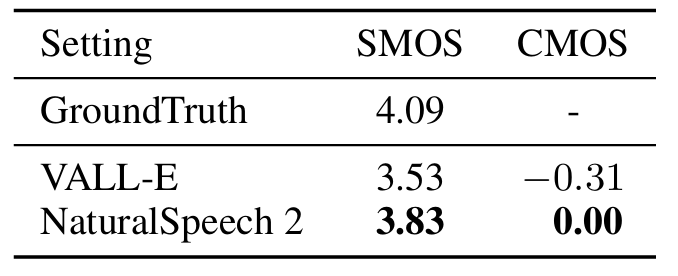
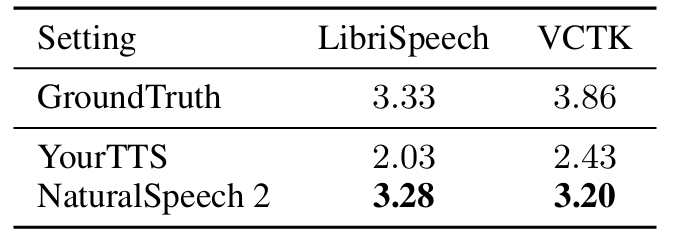
• Generation Similarity
  • Prosody similarity 측면에서 NaturalSpeech2가 가장 뛰어난 성능을 보임

Prosody Similarity

• SMOS도 마찬가지로 NaturalSpeech2가 가장 우수함

SMOS 비교

• Robustness
  • NaturalSpeech2는 가장 낮은 WER을 달성함

WER 비교

• NaturalSpeech2는 autoregressive model과 달리 word repeating, skipping 등이 나타나지 않음

Intelligibility

• Ablation Study
  • 각 component를 제거하는 경우 성능 저하가 발생함

Ablation Study

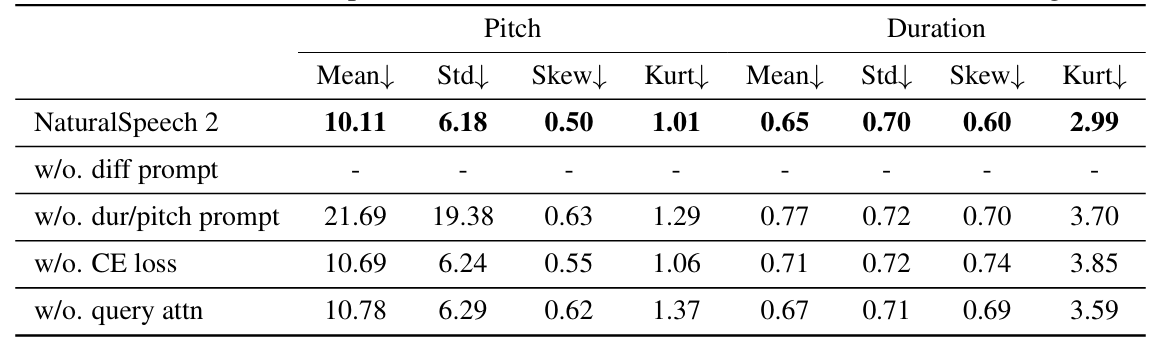
• 특히 long prompt를 사용할수록 prosody similarity가 향상됨

Prompt Length 별 Similarity