[Paper 리뷰] SECodec: Structural Entropy-based Compressive Speech Representation Codec for Speech Language Models

SECodec: Structural Entropy-based Compressive Speech Representation Codec for Speech Language Models

---

• Large Language Model을 위한 기존의 speech representation discretization method는 Euclidean distance-based quantization이나 pre-defined codebook에 의존함
• SECodec
  • Speech를 graph로 modeling 하고 graph 내의 speech feature node를 clustering 한 다음, 2D Strutural Entropy를 minimize 하여 codebook을 추출
    - 2D SE minimization principle을 따라 incoming original speech node에 대해 cluster의 most suitable token을 adaptively select 함
  • 추가적으로 SECodec을 활용한 Structural Entropy-based Speech Language Model을 구축
• 논문 (AAAI 2025) : Paper Link

---

1. Introduction

• Speech Large Language Model (LLM)은 speech processing에서 우수한 성능을 보이고 있음
  • 이때 continuous speech와 token-based language model 간의 gap을 bridge 하기 위해, audio signal을 finite token set로 변환하는 speech discretization이 사용됨
    - Speech를 discrete token으로 변환함으로써 language model은 future semantic content를 predict 하고 long-term consistency를 가진 realistic speech를 생성할 수 있음
  • 한편으로 discrete speech representation은 다음 3가지로 분류됨:
    1. Semantic token
       - Semantic token은 HuBERT, Wav2Vec 2.0과 같이 masked language modeling을 training objective로 사용하는 self-supervised pre-trained model로부터 얻어짐
       - TWIST와 같이 semantic token을 사용하는 speech LLM은 semantically accurate content를 capture 할 수 있지만, acoustic detail 측면에서 한계가 있음
    2. Acoustic token
       - Acoustic token은 SoundStream, EnCodec, HiFi-Codec, FunCodec과 같이 reconstruction을 training objective로 사용하는 neural audio codec을 통해 얻어짐
       - 대표적으로 VALL-E는 acoustic token을 사용하여 zero-shot text-to-speech (TTS)를 수행함
       
    3. Hybrid token
       - Hybrid token은 AudioLM, SpeechTokenizer와 같이 semantic, acoustic token을 combine하여 사용함
       
  • Ideal speech representation은 다음을 만족해야 함:
    1. Speech information의 effective preservation
       - BUT, 기존의 discretization method는 $k$-means와 empirical 하게 결정되는 codebook size에 의존함
    2. Efficient training을 위한 sufficient compressiveness
       - Euclidean-based quantization process는 codebook vector와 original vector 간의 substantial difference로 이어지므로, audio distortion이 발생할 수 있음

-> 그래서 effective preservation, sufficient compressiveness를 만족하는 neural codec인 SECodec을 제안

 

• SECodec
  • Structural Entropy (SE) minimization를 도입하여 speech codec representation을 modeling
    - Structural information과 Entropy guidance를 통해 pre-determined codebook size 없이도 compressive, informative codebook을 학습할 수 있음
  • Codebook size control 시 발생하는 audio distortion 문제를 해결하기 위해, SE heuristic function을 사용하여 added original speech feature에 적합한 cluster를 iteratively select 하는 quantization method를 구성
  • 추가적으로 SECodec에 기반한 speech LLM인 SESLM을 구축하여 zero-shot TTS task에 적용

< Overall of SECodec >

• Structural Entropy를 기반으로 한 speech representation codec
• 결과적으로 기존보다 뛰어난 성능을 달성

2. Preliminary

• Structural Entropy (SE)는 graph에서 random walk의 step을 통해 accessible vertex를 encode 하는데 필요한 minimum bit 수로 정의됨
  • 즉, SE는 graph의 hierarchical topology에 대한 uncertainty를 characterizing 하여 tree structure를 encoding 함으로써 graph complexity를 측정함
  • Graph $G$에 대한 SE는 encoding tree $\mathcal{T}$로부터 정의되고, $\mathcal{T}$에 의해 encode 된 다음 $G$에 남은 것은 uncertainty의 양을 나타냄
    - 이때 SE minimization을 통해, $G$의 vertice에 대한 optimized hierarchical clustering results는 $\mathcal{T}$에 의해 retain 됨 
• Encoding Tree와 SE에 대한 definition은 아래와 같음:
  • 먼저 $G=(V,E,W)$를 undirected weighted graph, $V=\{v_{1},...,v_{n}\}$을 vertex set, $E$를 edge set, $W\in\mathbb{R}^{n\times n}$을 edge weight matrix라고 하자 
  • [Definition 1]
    1. Graph $G$의 encoding tree $\mathcal{T}$는, 각 tree node $\alpha$가 vertex set $T_{\alpha}$와 associate 된 hierarchical rooted tree이다.
    2. $\mathcal{T}$의 root node $\lambda$는 $T_{\lambda}=V$에 associate 되고, 각 leaf node $v$는 $V$의 vertex를 포함하는 $T_{v}$에 associate 된다.
    3. 각 non-leaf node $\alpha\in\mathcal{T}$에 대해, $\alpha$의 successor는 disjoint vertex subset에 associate 하고, 이때 해당 subset의 union은 $T_{\alpha}$이다.
  • [Definition 2]
    1. $\mathcal{T}$가 주어졌을 때, $G$의 Structural Entropy는 다음과 같이 formulate 된다:
       (Eq. 1) $\mathcal{H}^{\mathcal{T}}(G)=\sum_{\alpha\in\mathcal{T},\alpha\neq\lambda}\mathcal{H}^{\mathcal{{T}}}(G;\alpha) = \sum_{\alpha\in\mathcal{T},\alpha\neq\lambda} -\frac{g_{\alpha}}{\mathcal{V}_{G}}\log_{2}\frac{\mathcal{V}_{\alpha}}{\mathcal{V}_{\alpha^{-}}}$
       - $\mathcal{H}^{\mathcal{T}}(G;\alpha)$ : $\alpha$의 assigned structural entropy
       - $g_{\alpha}$ : cut으로써, $T_{\alpha}$에 속하는 vertex와 속하지 않은 vertex 간의 edge weight summation
       - $\mathcal{V}_{\alpha},\mathcal{V}_{G}$ : volume으로써, 각각 $T_{\alpha}, G$에 대한 vertex degree의 summation
    2. 그러면 $\mathcal{T}$가 모든 possible encoding tree의 range를 나타낸다고 할 때, $G$의 structural entropy는 $\mathcal{H}(G)=\min_{\mathcal{T}}\left\{\mathcal{H}^{\mathcal{T}}(G)\right\}$와 같이 정의된다. 여기서 tree node와 associate 된 vertex set은 $V$ 내의 vertex에 대한 clustering을 구성한다.
  • [Definition 3]
    1. $K$D structural entropy는 height가 $K$ 이하인 encoding tree에서 주어지는 structural entropy이다. $K=2$일 때 encoding tree는 graph partitioning을 나타내므로, 이를 통해 partitioning clustering을 수행할 수 있다.
    2. 이때 $\mathcal{X}_{i}$를 root $\lambda$의 $i$-th children과 associate 된 module인 vertex set이라고 하면, 2D encoding tree $\mathcal{T}$는 $V$의 graph partitioning $\mathcal{P}=\{\mathcal{X}_{1},\mathcal{X}_{2},...,\mathcal{X}_{L}\}$로 formulate 될 수 있다.
    3. 결과적으로 $\mathcal{P}$가 주어졌을 때, $G$의 structural entropy는 다음과 같이 정의된다:
       (Eq. 2) $\mathcal{H}^{\mathcal{P}}(G)=-\sum_{\mathcal{X}\in\mathcal{P}}\sum_{v_{i}\in\mathcal{X}} \frac{g_{i}}{\mathcal{V}_{G}}\log_{2}\frac{d_{i}}{\mathcal{V}_{\mathcal{X}}}-\sum_{\mathcal{X}\in\mathcal{P}}\frac{g_{\mathcal{X}}}{\mathcal{V}_{G}}\log_{2}\frac{\mathcal{V}_{\mathcal{X}}}{\mathcal{V}_{G}}$
       - $d_{i}$ : vertex $v_{i}$의 degree, $g_{i}$ : cut으로써, $v_{i}$와 다른 vertex를 connect 하는 edge weight의 summation
       - $\mathcal{V}_{\mathcal{X}},\mathcal{V}_{G}$ : volume으로써, 각각 module $\mathcal{X}$와 graph $G$에 대한 vertex degree의 summation
       - $g_{\mathcal{X}}$ : cut으로써, module $\mathcal{X}$에 포함된 vertex와 포함되지 않은 vertex 간의 edge weight에 대한 summation

3. Method

• SECodec은 FunCodec의 RVQ-GAN framework를 기반으로 함
  - 전체적으로 SoundStream, EnCodec과 유사하지만, 2D SE를 통해 codebook initialization과 quantization process를 optimize 하여 compressive codebook과 informative token을 얻음

- Problem Formalization

• $H$는 speech representation dimension, $T$는 sequence length이고, pre-trained convolutional network에서 input speech feature $X=[x_{1},...,x_{T}]\in\mathbb{R}^{H\times T}$가 주어진다고 하자
  • 먼저 논문은 speech feature graph $G=(V,E,W)$를 구축함
    - $V=\{v_{1},v_{2},...,v_{n}\}$ : $X$의 speech feature에 해당하는 vertex set, $E$ : vertex를 connect 하는 edge set
    - $W$ : 각각의 speech feature frame 간의 similarity를 measure 하는 edge weight set으로써, speech feature의 두 가지 frame $x_{i},x_{j}\in X$에 대한 cosine-similarity로 얻어짐
  • $G$에 대한 partitioning은 $\{\mathbf{e}_{1},...,\mathbf{e}_{i},...,\mathbf{e}_{j},...,\mathbf{e}_{K}\},\,\mathbf{e}_{i}\subset V,\,\mathbf{e}_{i}\cap\mathbf{e}_{j}=\emptyset$을 생성함
    - 이는 $K$ cluster (set)을 포함하는 $V$의 partitioning을 의미하고, 해당 cluster는 codebook $\mathcal{E}_{codebook}=[\mathbf{e}_{1},...,\mathbf{e}_{K}]$에 해당함

Codebook Construction Algorithm

- Codebook Construction via Hierarchical and Disentangled 2D SE Minimization

• Speech feature graph partitioning은 $G$를 $\mathcal{P}$로 decode 하여 speech feautre cluster form으로 codebook size를 정의함
  • $G$에서 speech feature correlation을 faithful decode 하면 related speech feature는 same cluster에 assign 되고 unrelated feature는 다른 cluster에 assign 됨
    - 한편으로 기존의 speech codec은 $k$-means를 통해 codebook space를 initialize 하므로 codebook이 empirically pre-determine 되어야 함
  • 이를 위해 논문은 2D SE minimization의 guidance 하에서 codebook partitioning을 수행함
    - 이를 통해 speech feature cluster에 대한 prior knowledge 없이도 raw graph에 inherent 된 second-order (cluster-wise) structure를 얻을 수 있음
  • 한편으로 encoding tree $\mathcal{T}$에서 두 node를 repeatedly merge 하여 2D SE를 minimum possible value로 decrease 하는 Vanilla Greedy 2D SE Minimization algorithm을 고려할 수 있음
    1. 해당 process는 supervision이나 pre-determined cluster 수 없이 graph를 partition 함
       - BUT, vanilla 2D SE minimization algorithm은 $\mathcal{O}(|V|^{3})$의 time-complexity를 가지므로 large, complex graph에 적용하기 어려움
    2. 추가적으로 논문은 clustering을 통해 codebook을 구성해야 하므로, codebook의 column vector는 가능한 멀리 spatially distribute 되고 overlapping을 방지해야 함
  • 따라서 hierarchical, disentangled manner로 codebook을 구축하기 위해, SECodec은 [Algorithm 1]과 같은 2D SE Minimization algorithm을 활용함
    1. (Line 1) 먼저 각각의 speech feature $x_{1},...,x_{T}$는 own cluster에 place 됨
    2. (Line 3-5) 이후 해당 cluster는 size $n$의 subset으로 divide 되고, (Line 6-16) 각 subset 내에서 vanilla greedy algorithm을 적용하여 cluster를 새로운 cluster로 merge 함
    3. (Line 17) 새로 얻어진 cluster는 next iteration을 진행하고, (Line 18-19) 해당 iterative process는 모든 speech feature cluster가 simultaneously consider 될 때까지 continue 됨
    4. (Line 20-21) 만약 subset 내에서 cluster를 merge 할 수 없다면 subset size $n$을 increase 하여 더 많은 cluster가 potential merge 될 수 있도록 함
    5. (Line 22-34) 최종적으로 codebook 내의 각 vector 간 mutual information을 minimize 하여 해당하는 codebook을 추출함
  • 아래 그림의 (A)는 node $x_{1}$에서 $x_{10000}$까지의 speech feature graph construction에 해당하고, (B)는 codebook construction process에 해당함:
    1. 먼저 $x_{1}$에서 $x_{10000}$는 각각의 separate cluster로 존재하고, size $n=1024$의 cluster를 고려하여 subgraph $G'$를 구성함
    2. 각 $G'$ 내의 cluster는 (B.1)과 같이 vanilla 2D SE minimization을 통해 merge 되어 $\mathcal{P}'$을 생성함
    3. Previous iteration의 partition은 (B.2)와 같이 전달되고, 최종적으로 모든 speech feature를 encompass 하는 $\mathcal{P}'$을 얻으면 process가 종료됨
  • 한편으로 codebook이 speech diversity를 further represent 할 수 있도록, $\mathcal{P}'$에 대한 각 cluster의 central feature를 disentangle 하는 Mutual Information Learning algorithm을 도입함
    1. $\mathbf{e}_{i},\mathbf{e}_{j}$ 간의 disentanglement에 대해, variational Contrastive Log-ratio Upper Bound (vCLUB)은 irrelevant information의 Mutual Information (MI) upper bound를 compute 함
    2. 이를 통해 서로 다른 cluster representation 간의 correlation을 decrease 함:
       (Eq. 3) $\hat{\mathcal{I}}(\mathbf{e}_{i},\mathbf{e}_{j})=\frac{1}{\mathcal{N}^{2}}\sum_{\mathcal{M}=1}^{\mathcal{N}}\sum_{\mathcal{J}=1}^{\mathcal{N}}\left[ \log f_{\psi}\left(\mathbf{e}_{i_{\mathcal{M}}}|\mathbf{e}_{j_{\mathcal{M}}}\right)-\log f_{\psi}\left( \mathbf{e}_{j_{\mathcal{J}}}|\mathbf{e}_{i_{\mathcal{M}}}\right)\right]$
       - $\{\mathbf{e}_{i},\mathbf{e}_{j}\}\in\mathbf{e}$, $\mathcal{N}$ : $\mathbf{e}_{i},\mathbf{e}_{j}$의 sample
       - $f_{\psi}(\mathbf{e}_{i}|\mathbf{e}_{j})$ : $f(\mathbf{e}_{i}|\mathbf{e}_{j})$를 approximate 하기 위한 parameter $\psi$를 가지는 variational distribution
       - $\hat{\mathcal{I}}$ : sample $\{\mathbf{e}_{i_{\mathcal{M}}}, \mathbf{e}_{j_{\mathcal{J}}}$의 vCLUB에 대한 unbiased estimator
       - $\mathcal{M},\mathcal{J}$ : $\mathbf{e}_{i},\mathbf{e}_{j}$의 sample
    3. 해당 (Eq. 3)을 minimize 하여 accent feature $\mathbf{e}_{i}$, speech feature $\mathbf{e}_{j}$ 간의 correlation을 decrease 할 수 있음
  • 최종적으로 아래 그림의 (B.3)과 같이 $\mathcal{P}'$의 각 cluster에 대한 central feature를 concatenate 하여 codebook $\mathcal{E}_{codebook}$의 column을 구성함
    - 즉, SECodec은 unsupervised, disentangled manner로 complex speech feature graph로부터 compressive codebook을 생성함

Overview

- Quantization via Node Game-based 2D SE Minimization

• 기존의 Residual Vector Quantization (RVQ)-based speech codec은 input vector를 codebook vector와 compare 하고 most similar vector의 index를 추출함
  • 이때 comparison은 vector 간의 Euclidean distance를 calculate 하여 얻어짐
    - BUT, high-dimensional space에서 Euclidean distance는 uniformly distribute 되므로 result를 distort 하고 quantized token의 quality에 영향을 줄 수 있음
  • 이를 위해 논문은 quantization을 위 그림의 (C.1)과 같이 graph node가 subgraph를 dynamically categorize 하는 process로 취급하고, new input feature는 (C.2)와 같이 added node로 취급함
    - 여기서 added node는 SE heuristic function을 통해 appropirate cluster를 iteratively select 하고, selected cluster는 (C.3)과 같이 speech token을 구성함
  • 먼저 speech feature graph와 해당 codebook set $E=[\mathbf{e}_{1},...,\mathbf{e}_{i},...,\mathbf{e}_{K}]$가 주어진다고 하자
    1. Added speech feature node는 current codebook $\mathbf{e}_{i}$를 select 하고, codebook set을 $ E'=[\mathbf{e}_{1},...,\mathbf{e}'_{i},...,\mathbf{e}_{K},\{x\}],\,(\mathbf{e}_{i}=\mathbf{e}'_{i}\cup\{x\})$로 change 함
    2. 그러면 speech feature graph의 2D SE change는:
       (Eq. 4) $\Delta_{select}(x,\mathbf{e}_{i})=\mathcal{H}^{\mathcal{T}}(G)-\mathcal{H}^{\mathcal{T}'}(G)= \sum_{n=1}^{|E|}H^{(2)}(\mathbf{e}_{n})-\sum_{n=1}^{|E'|}H^{(2)}(\mathbf{e}'_{n})$
       $\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, =-\frac{g_{\mathbf{e}_{i}}}{\mathcal{V}_{G}}\log\frac{\mathcal{V}_{\mathbf{e}_{i}}}{\mathcal{V}_{G}}+\frac{g_{\mathbf{e}'_{i}}}{\mathcal{V}_{G}}\log\frac{\mathcal{V}_{\mathbf{e}'_{i}}}{\mathcal{V}_{G}}- \frac{g_{\mathbf{e}'_{i}}}{\mathcal{V}_{G}}\log\frac{\mathcal{V}_{\mathbf{e}'_{i}}}{\mathcal{V}_{\mathbf{e}_{i}}}- \frac{d_{x}}{\mathcal{V}_{G}}\log\frac{\mathcal{V}_{G}}{\mathcal{V}_{\mathbf{e}_{i}}}$
       - $\Delta_{select}(x,\mathbf{e}_{i})$ : node $x$가 cluster $\mathbf{e}_{i}$를 select 할 때 2D SE change
       - $\mathcal{T}'$ : codebook set $\mathcal{E}$에 해당하는 encoding tree
       - $\mathcal{H}^{\mathcal{T}'}(G), \mathcal{H}^{\mathcal{T}}(G)$ : $E,E'$ 하에서 graph의 2D SE
       - $\mathcal{V}_{G},\mathcal{V}_{\mathbf{e}_{i}},\mathcal{V}_{\mathbf{e}'_{i}}$ : 각각 graph, cluster $\mathbf{e}_{i}$, cluster $\mathbf{e}'_{i}$의 volume
       - $g_{\mathbf{e}_{i}}, g_{\mathbf{e}'_{i}}$ : 각각 $\mathbf{e}_{i},\mathbf{e}'_{i}$의 total cut edge weight
    3. Added node는 2D SE의 smallest change value를 가진 codebook cluster만을 select, join 함:
       (Eq. 5) $t=\text{Min}\left(\Delta_{select}(x,\mathbf{e}_{i})\right)$
       - $t$ : target cluster index, $\text{Min}$ : smallest 2D SE change value에 해당하는 codebook index를 find 하는 operation

- Training Objective

• Training objective는 reconstruction loss, adversarial loss, RVQ commit loss로 구성됨
  • Reconstruction loss의 경우 time-domain에서 original speech와 reconstructed speech 간의 $L1$ distance를 minimize 하고, frequency-domain에서 multiple mel, magnitude spectra에 대한 $L1, L2$ distance를 minimize 함
  • Adversarial loss의 경우, Multi-Scale Discriminator (MSD), Multi-Period Discriminator (MPD), Multi-Scale STFT-based Discriminator (MSTFTD)를 incorporate 함

- SESLM

• 추가적으로 논문은 SECodec 기반의 Structural Entropy-based Speech Language Model (SESLM)을 구축함 
  • 구조적으로는 autoregressive, non-autoregressive model로 구성되어 speech information에 대한 hierarchical modeling을 지원함
    - 이때 VALL-E와 달리 autoregressive model part에 speech token input이 사용됨
  • 특히 SECodec을 통해 추출된 speech token을 richer speech information을 가지고 있음
    1. 따라서 SESLM은 textual prompt $u$와 acoustic prompt $\mathcal{S}$의 2가지 input prompt를 사용하여 neural code sequence에 대한 conditional generation $\mathcal{O}$를 수행함
    2. 그러면 training objective는:
       (Eq. 6) $ \mathcal{L}_{AR}=-\sum_{t=1}^{N}\log P\left(\mathcal{O}_{t,1}|u,\mathcal{S},\mathcal{O}_{<t,1};\theta_{AR}\right), \,\,\, \mathcal{L}_{NAR}=-\sum_{l=2}^{8}\log P\left(\mathcal{O}_{:,l},|u,\mathcal{S},\mathcal{O}_{:,<l};\theta_{NAR}\right)$
       - $\mathcal{O}_{<t,1} =[\mathcal{O}_{1,1},...,\mathcal{O}_{t-1,1}]$, $\theta_{AR}, \theta_{NAR}$ : AR Transformer, NAR model의 parameter
       - $\mathcal{O}_{:,l}$ : $l$-th layer에 대한 $\mathcal{O}_{t,l}$의 entire sequence, $\mathcal{O}_{:,<l}=[\mathcal{O}_{:,1},...,\mathcal{O}_{:,l-1}]$ : $l=2,...,8$에 해당함
  • AR model은 acoustic, textual prompt의 concatenated embedding에 대해 condition 되어 있음
    1. 추론 시 text input은 phoneme sequence로 변환되고, speech prompt는 speech token으로 변환됨
       - 이후 AR, NAR model에 대한 prompt를 구성하기 위해 concatenate 됨
    2. 최종적으로 SECodec decoder는 complete token matrix를 condition으로 하여 waveform을 생성함

4. Experiments

- Settings

• Dataset : LibriSpeech
• Comparisons : EnCodec, SpeechTokenizer

- Results

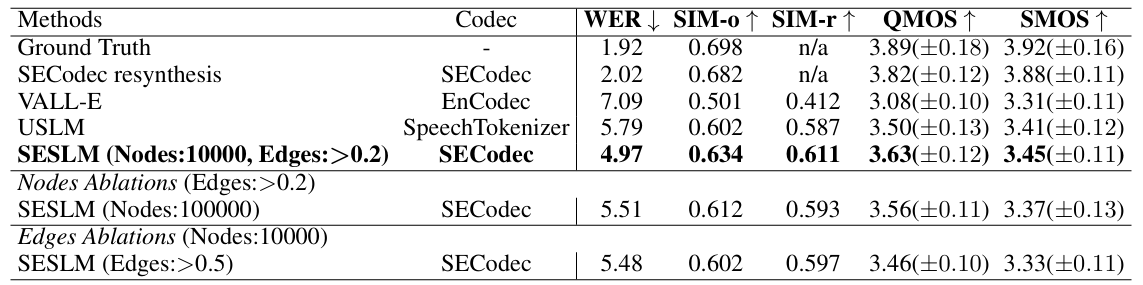
• 전체적으로 SECodec의 성능이 가장 우수함

Model 성능 비교

• Choice of Nodes and Edges for SE
  • $10000$ node, $0.2$ edge threshold를 사용할 때 최적의 성능을 달성함

Node, Edge에 대한 Choice 비교

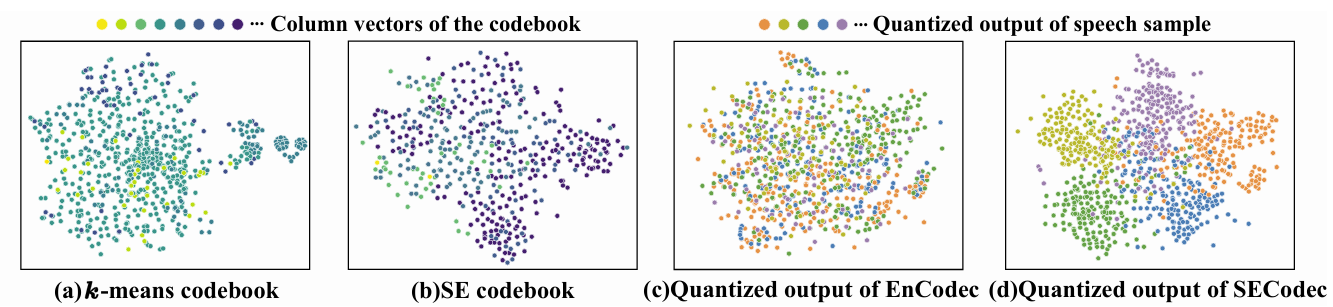
• Codebook and Quantized Output Visualization
  • Codebook의 각 column vector에 $t$-SNE를 적용해 보면, $k$-means로 initialize 된 codebook은 uneven distribution을 보이고 cluster center가 entangle, overlap 되어 있음
  • SECodec을 사용하는 경우 initialized codebook은 evenly distribute, discrete 하게 나타남

$t$-SNE

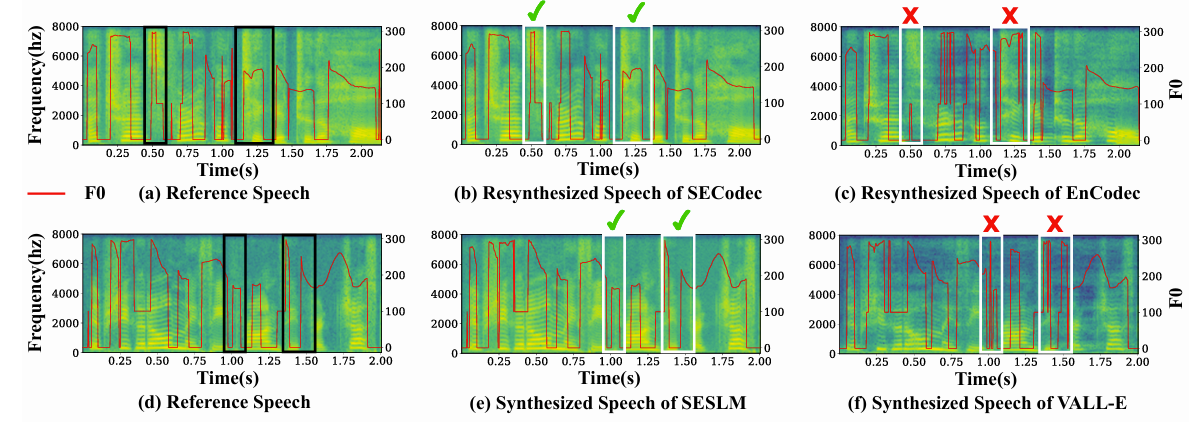
• Effectiveness of SE Qunatization
  • SECodec은 detailed feature를 preserve 하고 fundamental frequency $F0$ 측면에서 wave peak의 intricacy를 maintain 할 수 있음

SE Quantization 비교