[Paper 리뷰] RepCodec: A Speech Representation Codec for Speech Tokenization

RepCodec: A Speech Representation Codec for Speech Tokenization

---

• Discrete speech tokenization은 large language model에서 유용하게 활용되지만 discretization으로 인해 information loss가 발생함
• RepCodec
  • Speech encoder에서 speech representation을 reconstruction 하여 vector quantization codebook을 학습
  • Speech encoder, Codec encoder, Vector quantization codebook으로 구성된 pipeline을 통해 speech waveform을 semantic token으로 변환
• 논문 (ACL 2024) : Paper Link

---

1. Introduction

• Large Language Model (LLM)은 audio signal을 finite token set으로 discretize 하는 speech tokenization을 통해 continuous speech와 token-based language modeling을 bridge 할 수 있음
  • 이를 통해 AudioLM, VALL-E 등과 같이 Language Model은 future semantic content를 predict하고 long-term consistency를 가진 realistic speech를 생성할 수 있음
  • 한편으로 discrete speech token은 semantic token과 acoustic token으로 나눌 수 있음
    1. Acoustic token은 SoundStream, DAC와 같은 audio codec에 의해 생성되고, perceptually identical한 original audio를 reconstruct 하는 것을 목표로 함
       - BUT, audio의 모든 information을 preserve하면 acoustic token은 high-bitrate를 가지게 됨
       - 결과적으로 LLM에 상당한 computational demand를 impose 하고 lengthy sequence로 인한 문제가 발생할 수 있음
    2. Semantic token은 audio의 semantic information 만을 preserve 하여 lower bitrate를 가짐
       - 대표적으로 HuBERT는 $k$-means clustering을 활용하여 semantic token을 추출함
       - BUT, original speech representation에 비해 information이 loss될 수 있고, 모든 speech representation set가 clustering에 suitable 하지 않음

-> 그래서 더 나은 speech semantic token을 추출할 수 있는 RepCodec을 제안

 

• RepCodec
  • End-to-End neural codec을 활용하여 speech representation에 대한 더 많은 information을 preserve
  • 구조적으로는 Encoder, Vector Quantizer (VQ), Decoder로 구성되고, 특히 speech encoder, codec encoder, VQ codebook은 speech tokenization pipeline을 구축하여 low-bitrate, high-quality semantic token을 생성
  • Decoder-Only ASR, unit-to-speech generation task를 통해 downstream task에 대한 RepCodec 성능을 비교

< Overall of RepCodec >

• Representation 내의 information을 preserve하기 위해 neural compression technique을 도입
• 결과적으로 downstream task에 대해 기존보다 뛰어난 reconstruction 성능을 달성

2. Method

• Semantic token은 AudioLM과 같은 speech modeling에서 유용하게 활용되지만 discretization으로 인해 information loss가 발생할 수 있음
  • 결과적으로 information loss로 인해 ASR, speech translation 등의 downstream taks의 성능이 저하됨
  • 실제로 AudioLM에서 w2v-BERT XL의 $k$-means discrete token을 사용하는 경우 WER이 2.5%에서 6.0%로 증가함
  • 따라서 representation에 대한 discretization은 더 많은 information을 preserve 할 수 있어야 함

Overall of RepCodec

- Architecture of RepCodec

• Representation에 대한 효과적인 compression을 위해 RepCodec은 Codec Encoder, VQ Module, Codec Decoder로 구성된 parametric network를 활용함
  • Codec Encoder는 speech representation $\mathbf{X}=[\mathbf{x}_{1},...,\mathbf{x}_{T}]\in\mathbb{R}^{H\times T}$를 input으로 하여 latent representation $\mathbf{Z}=[\mathbf{z}_{1},...,\mathbf{z}_{T}]\in\mathbb{R}^{H\times T}$를 생성함
    - $H$ : speech representation dimension, $T$ : sequence length
  • 이후 $\mathbf{Z}$는 VQ module로 전달되어 codebook $\mathbf{E}=[\mathbf{e}_{1},...,\mathbf{e}_{K}]$를 가지는 discrete token $\mathbf{s}=s_{1}...s_{T}$의 sequence로 quantize 됨
    - $K$ : pre-determined cluster 수
  • Codec Decoder는 해당 token $\mathbf{E}$를 사용하여 original speech representation을 reconstruct 함
• Encoder and Decoder
  • Encoder-Decoder architecture는 SoundStream, AudioDec을 따름
  • Encoder는 input representation $\mathbf{X}$의 time-dimension에 대한 1D convolution layer로 구성됨
    - Encoder block에는 더 나은 optimization을 위한 residual path가 포함됨
  • Decoder도 마찬가지로 1D convolution layer와 residual path로 구성됨
    - 이때 RepCodec에서는 encoder/decoder 모두에서 down/upsampling을 수행하지 않고 representation의 frequency를 input과 동일하게 유지함
• Vector Quantizer
  • Vector Quantizer는 latent representation $\mathbf{Z}$를 discrete token series $\mathbf{s}$로 compress 함
    - 즉, latent $\mathbf{z}$를 closest codebook $\mathbf{e}_{k}$로 project 하고 $\mathbf{e}_{k}$를 decoder로 output 함
  • 여기서 RepCodec은 regular VQ와 RVQ를 고려함
    - 특히 RVQ는 previous layer의 residual을 quantize 하는 $M$-layer quantizer로써, $M=1$일 때 VQ와 동일함

Encoder-Decoder Architecture

- Training Objective

• Training objecitve는 downstream task를 위해 가능한 많은 information을 preserve 하는 것을 목표로 $\mathbf{X}$에 대한 reconstruction loss, VQ training을 위한 quantization loss로 구성됨
  • Reconstruction Loss $l_{r}$
    1. Reconstruction loss는 input representation $\mathbf{X}$와 output representation $\hat{\mathbf{X}}$간의 squared $\ell_{2}$ loss를 minimize 함:
       (Eq. 1) $l_{r}=\frac{1}{HT}|| \mathbf{X}-\hat{\mathbf{X}}||_{F}^{2}$
    2. $H$ : representation의 hidden dimension, $||\cdot||_{F}$ : Forbenius norm
  • Quantization Loss $l_{q}$
    1. DAC를 따라 encoder output과 VQ의 quantized value 간에 quantization loss $l_{q}$를 적용함
    2. 즉, latent representation $\mathbf{Z}=[\mathbf{z}_{1},\mathbf{z}_{2},...,\mathbf{z}_{t}]$와 codebook $\mathbf{E}=[\mathbf{z}_{1},\mathbf{z}_{2},...,\mathbf{z}_{K}]$가 주어졌을 때 다음의 (Eq. 2)를 minimize 함:
       (Eq. 2) $l_{q}=\frac{1}{T}\sum_{t=1}^{T}\frac{1}{H}\sum_{k=1}^{K}\mathbb{I}_{k}(\mathbf{z}_{t})|| \mathbf{z}_{t}-\mathbf{e}_{k}||_{2}^{2}$
       - $\mathbb{I}_{k}(\mathbf{z}_{k})\in\{0,1\}$ : data point $\mathbf{z}_{t}$가 $K$ cluster 중 어느 cluster에 assign되었는지를 indicating하는 binary indicator variable
       - $\mathbf{z}_{t}$가 cluster $k$에 assign 되는 경우 $\mathbb{I}_{k}(\mathbf{z}_{k})=1$이고, 그렇지 않은 경우 $\mathbb{I}_{k}(\mathbf{z}_{k})=0$
    3. RVQ를 사용하는 경우, (Eq. 2)의 quantization loss는:
       (Eq. 3) $l_{q}=\sum_{i=1}^{M}\frac{1}{T}\sum_{t=1}^{T}\frac{1}{H}\sum_{k=1}^{K}\mathbb{I}_{k}^{i}(\mathbf{z}_{t}^{i})||\mathbf{z}_{t}^{i}-\mathbf{e}_{k}^{i}||_{2}^{2}$
       - $i\in [1,M]$ : RVQ의 $i$-th quantizer
       - $\mathbb{I}_{k}^{i},\mathbf{z}_{t}^{i},\mathbf{e}_{k}^{i}$ : 각각 $i$-th indicator, input representation, quantizer codebook
  • $l_{q}$는 encoder parameter를 updating 하는데만 사용되어 encoder latent representation $\mathbf{Z}$를 quantizer clustering에 suitable 하게 만듦
    - 여기서 quantizer는 Exponential Moving Average (EMA)에 의해 update 됨
  • 결과적으로 RepCodec은 두 loss의 combination으로 training 됨:
    (Eq. 4) $l=\lambda_{r}\cdot l_{r}+\lambda_{q}\cdot l_{q}$

- Optimization of Vector Quantizer

• $k$-means, VQ 모두 high-dimensional vector를 discrete label로 discretize 함
  • 이때 공통적으로 (Eq. 2)에서 $\ell_{2}$로 측정된 best cluster를 찾는 objective function을 optimize 함
    1. 이를 위해 $k$-means는 EM algorithm을 채택함
       - BUT, sharp change로 인해 quantization module을 통한 gradient back-propagation이 hinder 되므로 training process가 instable 해짐
    2. Straight-through Gradient Method, Exponential Moving Average (EMA), Gumbel Softmax 등을 채택한 VQ 방식은 quantization을 gradually change 할 수 있음
       - 결과적으로 encoder의 stable update를 보장할 수 있으므로 end-to-end training이 가능해짐
  • 따라서 RepCodec은 SoundStream을 따라 EMA algorithm을 채택함
    1. 구체적으로 $\{\mathbf{z}_{1},...,\mathbf{z}_{b}\}$의 minibatch input이 주어졌을 때, codebook entriy $\mathbf{e}_{k}$는 EMA에 의해 factor $0\leq\gamma \leq 1$로 update 됨
       - $b$ : batch size
    2. 여기서 $\tilde{n}_{k}, \tilde{\mathbf{e}}_{k}$를 각각 moving average, $k$-th cluster codebook라 하고, $\mathbb{I}_{k}(\mathbf{z}_{j})$가 $j$-th feature가 $k$-th cluster에 속한다는 indicator를 의미한다고 하면:
       (Eq. 5) $\tilde{n}_{k}=\gamma\tilde{n}_{k}+(1-\gamma)\sum_{j=1}^{b}\mathbb{I}_{k}(\mathbf{z}_{j}),$
       $\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \tilde{\mathbf{e}}_{k}=\gamma\tilde{\mathbf{e}}_{k}+(1-\gamma)\sum_{j=1}^{b}\mathbb{I}_{k}(\mathbf{z}_{j})\mathbf{z}_{j}$

- Downstream Tasks

• Semantic token의 성능을 확인하기 위해 decoder-only ASR과 unit-to-speech generation의 downstream task를 활용함
  • 이때 각 language model의 audio input/output을 simulation 하고 WER을 통해 token이 capture 한 semantic information 양을 측정함
  • Speech Resynthesis and Voice Conversion
    1. 각 token set에 대한 speech resynthesis를 위해 unit-based HiFi-GAN vocoder를 활용함
       - Vocoder는 generator-discriminator loss와 log-domain의 unit segment에 대한 Mean Squared Error (MSE)를 결합하여 training 됨
    2. 이후 AudioLM과 같이 Whisper large-v2 model을 사용하여 resynthesized speech의 ASR-WER을 측정하여 token quality를 evaluate 함
       - Acoustic quality는 $F0$ error, MOS를 활용함
  • Decoder-Only ASR
    1. 추가적으로 decoder-only transformer를 활용하여 RepCodec을 evaluate 할 수 있음
    2. 먼저 Semantic audio token series $\mathbf{s}=s_{1}s_{2}...s_{T}$와 해당 transcript $\mathbf{y}=y_{1}y_{2}...y_{m}$이 주어지면 다음의 sequence를 얻을 수 있음:
       (Eq. 6) $\mathbf{p}=s_{1}s_{2}...s_{n}<|\text{transcribe}|>y_{1}y_{2}...y_{m}$
       - $<|\text{transcribe}|>$ : transcription start를 indicate 하는 special token
       
    3. ASR은 sequence-to-sequence task이므로 $p(\mathbf{s},\mathbf{y})$에 대한 full language modeling 대신 conditional probability를 maximize 하는 transformer $F$를 find 함:
       (Eq. 7) $F_{*}=\arg\max_{F}p(\mathbf{y}|\mathbf{s})=\arg\max_{F}\prod_{i=1}^{m}p(y_{i}|y_{<i},\mathbf{s})$
       - $p(\mathbf{s},\mathbf{y})$에 대한 full language modeling은 $p(\mathbf{y}|\mathbf{s})$ 보다 낮은 성능을 보이기 때문

$p(\mathbf{s},\mathbf{y}), p(\mathbf{y}❘\mathbf{s})$ 비교

3. Experiments

- Settings

• Dataset : LibriSpeech, MLS
• Comparisons : $k$-means, VQ, EnCodec

- Results

• Decoder-Only ASR
  • ASR task에 대해 RepCodec이 가장 우수한 성능을 보임

Decoder-Only ASR

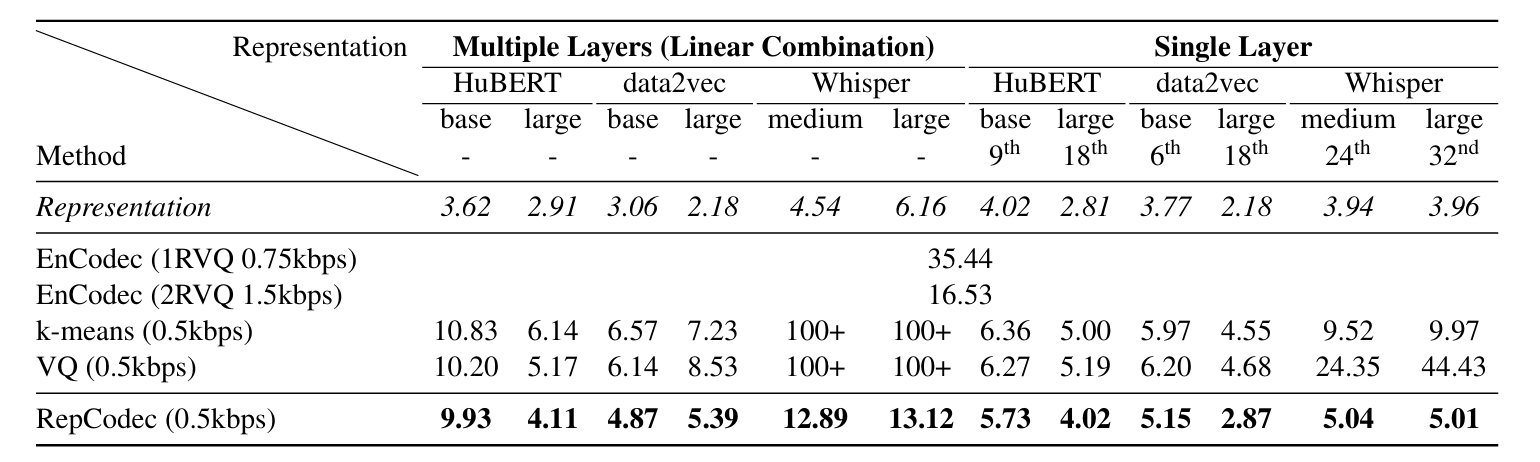
• 아래의 (a)와 같이 large RepCodec을 사용하는 경우 더 낮은 WER을 달성할 수 있음
  
  • (b)와 같이 2-layer RVQ를 사용하는 경우 speech representation에 대한 더 많은 information을 preserve 할 수 있음
  • (c)와 같이 cluster 수 $K$가 다르더라도 RepCodec은 $k$-means, VQ 보다 뛰어난 성능을 보임
  • (d)와 같이 multilingual setting에서도 RepCodec은 우수한 성능을 보임

다양한 설정에서의 RepCodec 성능 비교

• Speech Resynthesis and Voice Conversion
  • Resynthesis, Voice Conversion task에 대해서도 RepCodec이 가장 우수한 성능을 달성함

Resynthesis, Voice Conversion 성능

• Acoustic quality 측면에서도 안정적인 성능을 보임

Acoustic Quality

• Phone-Normalized Mutual Information (PNMI) vs. Reconstruction Loss
  • Reconstruction loss, PNMI 모두 RepCodec training이 진행됨에 따라 decrease 함
  • Higher PNMI는 downstream task에서 lower WER을 의미하지 않지만 clustering reconstruction loss와는 positively correlate 되어 있음
    

Reconstruction loss vs. PNMI

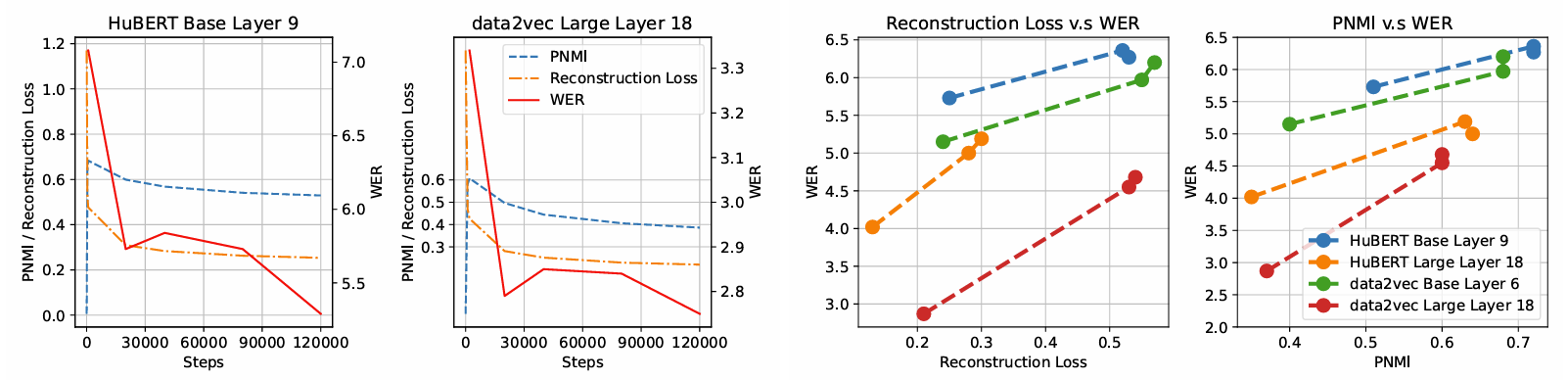
• Interpretability of RepCodec
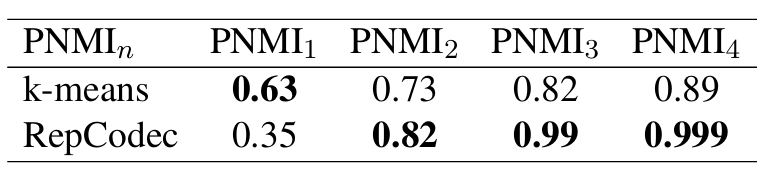
  • RepCodec token sequence는 phoneme sequence에 해당함
  • 따라서 discrete token과 phoneme sequence 간의 correspondence를 측정하기 위해 $n$-gram token에 대한 PNMI를 다음과 같이 extend 할 수 있음:
    (Eq. 8) $\text{PNMI}_{n}=\frac{I(s_{j}:s_{j+n};z_{j}:z_{j+n})}{H(s_{j}:s_{j+n})}$
    - $z_{j}:z_{j+n}$ : $j$-th frame에서 starting 하는 length $n$의 semantic token sequence
    - $s_{j}:s_{j+n}$ : length $n$의 phoneme sequence
    - $I$ : mutual information, $H$ : entropy
  • 결과적으로  $k$-means의 $\text{PNMI}_{1}$은 RepCodec보다 높지만, longer token sequence의 경우 RepCodec의 $\text{PNMI}_{n}$은 $k$-means보다 높아짐
    - 즉, word, sentence와 같은 longer sequence에 대해 RepCodec은 downstream decoder가 해당 task를 학습하는데 필요한 deterministic information을 제공함

$\text{PNMI}_{n}$ 비교