[Paper 리뷰] Generative De-quantization for Neural Speech Codec via Latent Diffusion

Generative De-quantization for Neural Speech Codec via Latent Diffusion

---

• Low-bitrate speech coding에서 end-to-end network는 compact, expressive feature와 powerful decoder를 학습하는 것을 목표로 함
  - BUT, 여전히 complexity와 speech quality 측면에서 한계가 있음
• LaDiffCodec
  • Low-dimensional discrete token을 학습하기 위해 end-to-end codec을 구성
  • Latent diffusion model을 사용하여 coded feature를 high-dimensional continuous space로 de-quantize
  • 추가적으로 over-smooth generation을 해결하기 위해 midway-infilling을 도입
• 논문 (ICASSP 2024) : Paper Link

---

1. Introduction

• Neural speech codec은 human speech의 intrictate pattern을 효과적으로 capture 할 수 있음
  • 기존의 neural codec은 waveform coding을 기반으로 single network에서 expressive latent feature를 추출하는 것을 목표로 encoder-decoder를 end-to-end training 함 
    1. 결과적으로 충분한 data가 주어지면 end-to-end model은 high-fidelity의 reconstruction이 가능함
    2. 대표적으로 SoundStream은 fully convolutional architecture와 residual vector quantization을 사용하여 3kpbs에서 최상의 품질을 달성
    3. 그 외에도 EnCodec, DAC 역시 뛰어난 speech coding 품질을 보임
       - BUT, 해당 방식들은 대부분 3kbps 이상의 medium/high bitrate에서만 효과적으로 동작하고, low-bitrate의 경우 low-dimensional representation을 학습하기 위해 deep, complex network가 필요함 
  • 따라서 low-bitrate를 효과적으로 coding 하기 위해, 일반적으로 generative model을 활용한 vocoder-based codec을 구성함
    - 특히 LMCodec은 SoundStream에 AudioLM을 적용하여 bitrate를 1kpbs로 줄임
  • 추가적으로 waveform codec의 low-bitrate coded feature는 동일한 bitrate에서 기존의 speech feature보다 distinguishable feature를 preserve 하고 essential information을 더 잘 capture 할 수 있음 
    
    1. 이때 generative modeling을 위해 diffusion model을 채택하면 natural-sounding audio를 얻을 수 있음
       - Autoregressive model과 달리 diffusion model은 large condition space를 고려하므로 quality upper bound가 크게 증가하기 때문
    2. 특히 Latent Diffusion (LD) model은 raw waveform reconstruction에 대한 diffusion model의 부담을 줄일 수 있음
       

-> 그래서 end-to-end audio coding으로 학습된 representation을 기반으로 powerful generative method인 diffusion model을 적용한 LaDiffCodec을 제안

 

• LaDiffCodec
  • Continuous, high-dimensional latent space에 의해 bottleneck이 정의되는 autoencoder를 활용
    - 이때 decoder는 de-quantization과 dimension expansion task에 대해 exempt 되므로 high-fidelity reconstruction을 담당한다고 가정함
  • Bottleneck 내에서 quantization과 dimension reduction을 수행하는 추가적인 end-to-end codec을 도입
    - 해당 end-to-end codec은 low-bitrate code에서 coarse reconstruction을 수행함
  • 최종적으로 두 feature representation 간의 gap을 bridge 하는 latent diffusion model을 적용
    1. 이를 통해 end-to-end codec의 lower-dimensional quantized code로 diffusion model을 conditioning 함으로써 generative de-quantization과 upsampling task를 수행하도록 함
    2. 추가적으로 diffusion model의 over-smooth generation과 hallucinate content를 방지하기 위해 conditional generation에 strong prior를 추가하는 midway-infilling을 도입

< Overall of LaDiffCodec >

• Latent diffusion model을 활용한 end-to-end speech codec
• 결과적으로 high-/low-bitrate 모두에서 기존보다 우수한 합성 품질을 달성

2. Method

• LaDiffCodec은 discrete coding module에서 생성된 quantized code를 continuous code로 변환하는 latent diffusion process로 구성됨

Overall of LaDiffCodec

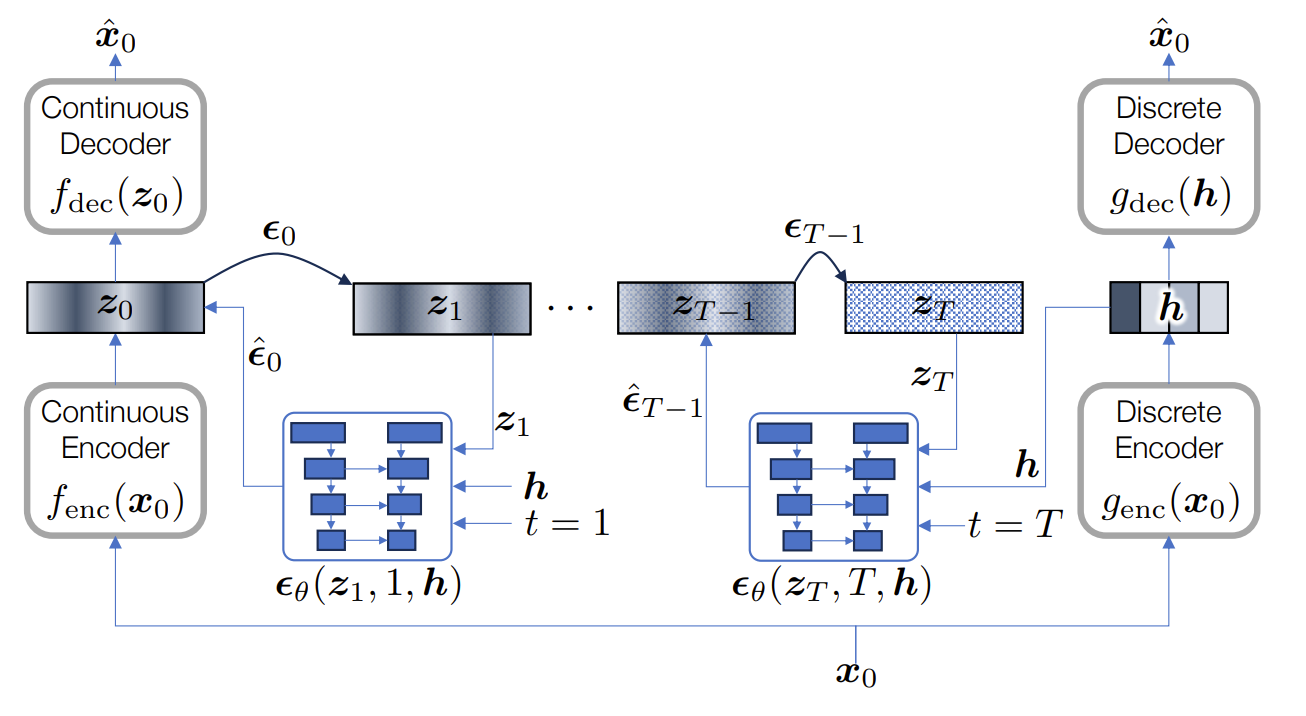
- Latent Diffusion

• Diffusion model은 diffusion/reverse process로 characterize 되는 2개의 Markov chain으로 구성되는 generative model
  • 먼저 diffusion process $q(\mathbf{x}_{1:T}|\mathbf{x}_{0})=\prod_{t=1}^{T}q(\mathbf{x}_{t}|\mathbf{x}_{t-1})$는 standard normal distribution에 가까운 random variable $\mathbf{x}_{T}$에 도달할 때까지 점진적으로 Gaussian noise를 추가하여 clean data point $\mathbf{x}_{0}$를 corrupt 함
    1. 즉, $\beta_{t}$를 pre-defined noise schedule ($0<\beta_{0}<...<\beta_{T}<1$)이라고 할 때, $q(\mathbf{x}_{t}|\mathbf{x}_{t-1})\sim\mathcal{N}(\sqrt{1-\beta_{t}}\mathbf{x}_{t-1},\beta_{t}I)$
    2. Reparameterization을 통해 얻어지는 diffusion process의 sampling step $\mathcal{F}:\mathbf{x}_{0}\mapsto \mathbf{x}_{t}$은:
       (Eq. 1) $\mathcal{F}(\mathbf{x}_{0},t)=\sqrt{\bar{\alpha}_{t}}\mathbf{x}_{0} +\sqrt{1-\bar{\alpha}_{t}}\epsilon$
       - $\epsilon\sim \mathcal{N}(0,1)$, $\bar{\alpha}_{t}=\prod_{i=0}^{t}(1-\beta_{i})$
  • Learned reverse process $p_{\theta}(\mathbf{x}_{0:T})=p(\mathbf{x}_{T})\prod_{t=1}^{T}p_{\theta}(\mathbf{x}_{t-1}|\mathbf{x}_{t})$는 일반적으로 parameteric function으로 represent 됨
    1. e.g.) data point $\mathbf{x}_{t}$를 denoise 하기 위해 step $t$에서 noise $\epsilon_{t}$를 예측하는 neural network
    2. 해당 process는 다양한 auxiliary function에 의해 condition 될 수 있음
  • Diffusion model은 우수한 생성 품질에 비해 computational complexity가 높으므로, 논문은 pre-trained autoencoder에 의해 학습되는 latent space $\mathbf{z}$에 기반한 latent diffusion (LD) model을 채택:
    (Eq. 2) $\hat{\mathbf{x}}_{0}\leftarrow f_{\text{dec}}(\mathbf{z}),\,\,\, \mathbf{z}_{0}\leftarrow f_{\text{enc}}(\mathbf{x}_{0})$
    - 이때 해당 latent space는 computationally preferable 하고 data domain과 perceputally equivalent 하다고 가정
    - 그러면 LD의 diffusion process는 latent space에서 $q(\mathbf{z}_{1:T}|\mathbf{z}_{0})=\prod_{t=1}^{T}q(\mathbf{z}_{t}|\mathbf{z}_{t-1})$과 같이 정의됨

- Diffusion-based De-quantization

• LaDiffCodec은 low-dimensional discrete code $\mathbb{H}$와 high-dimensional continuous feature $\mathbb{Z}$에 대한 2개의 latent space를 mapping 함 
  • 이때 해당 mapping의 resotrative nature는 conditional generation을 요구함
    - 따라서 LaDiffCodec은 discrete coding, cotinuous coding, conditional diffusion sampling을 활용
  • Discrete Coding
    1. Discrete coding module $g(\cdot)$은 encoder component $g_{\text{enc}}:\mathbb{R}^{N}\rightarrow \mathbb{H}^{D}$를 사용하여 discrete code space $\mathbb{H}$를 학습하는 autoencoder-type codec 
       - 이를 통해 transmission bitstream 역할을 하는 discretized feature $\mathbf{h}\in\mathbb{H}^{D}$를 얻음
    2. 논문은 해당 autoencoder codec을 통해 quantized speech token $\mathbf{h}$가 faithful speech reconstruction을 위한 충분한 information을 포함하도록 함
       - 한편 기존 codec은 decoder function $g_{\text{dec}}:\mathbb{H}^{D}\rightarrow \mathbb{R}^{N}$에만 의존하므로, $\mathbb{H}^{D}$가 low-dimensional 하고 discrete 할 때 bottleneck이 발생할 수 있음
    3. 따라서 LaDiffCodec은 해당 discrete code $\mathbf{h}$를 repurpose 하여 reverse diffusion process를 condition 함 
       - 이를 위한 discrete coding module의 backbone으로써 EnCodec을 채택
  • Continuous Coding
    1. Discrete token $\mathbf{h}$를 continuous feature vector $\mathbf{z}$로 de-quantize 하기 위해 LaDiffCodec은 continuous space $\mathbb{Z}$에서 정의되는 LD model을 구성함 
    2. 이를 위해 논문은 raw signal space $\mathbb{X}$를 feature space $\mathbb{Z}$에 mapping 하는 또 다른 Encodec-like continuous autoencoder $f_{\text{enc}} : \mathbb{X}^{N}\rightarrow \mathbb{Z}^{L}$를 도입
       - 이후 signal domain으로 mapping 하는 decoder $f_{\text{dec}}:\mathbb{Z}^{L}\rightarrow \mathbb{X}^{N}$을 추가
    3. 이때 해당 continuous latent space에는 trade-off가 존재함
       - 즉, high-expressiveness를 위해서는 latent dimension $L$을 증가시키면 되지만, high-dimensionality로 인해 sampling time이 길어짐
       - 추가적으로 high-dimensional continuous space와 low-dimensional discrete space 간의 gap을 upsampling layer로 fill 해야 하므로 additional artifact가 발생할 수 있음
  • Conditional Latent Diffusion
    1. $\mathbb{Z}$를 기반으로 구축된 diffusion model은 diffusion process에서 점진적으로 noise $\epsilon_{t}$를 $\mathbf{z}_{t}$에 추가함 
    2. 여기서 denoising (reverse) process를 학습하기 위해 reweighted training objective로 $\epsilon_{t}$를 추정하는 conditional neural network model을 사용함:
       (Eq. 3) $\mathbb{E}_{\mathbf{z}_{0},t,\mathbf{h}}\left( || \epsilon_{t}-\epsilon_{\theta}(\mathbf{z}_{t},t,\mathbf{h}) ||\right)$
       - $\epsilon_{\theta}(\mathbf{z}_{t},t,\mathbf{h})$ : weight $\theta$로 parameterize 된 nerual network
    3. (Eq. 3)은 generation process에서 발생하는 noise를 예측하므로, loss는 $\epsilon_{t}$와 예측값 간의 차이로 계산됨
       - Quantized feature $\mathbf{h}$는 generation을 steer 하기 위해 training/sampling stage 모두에 condition 됨

- Midway-Infilling

• DDPM의 기존 sampling algorithm은 noisy data sample에서 예측된 noise $\epsilon_{\theta}$를 iteratively remove 함
  • 이때 $\mathcal{G}:\mathbf{x}_{t}\mapsto\mathbf{x}_{t-1}$는:
    (Eq. 4) $\mathcal{G}(\mathbf{x}_{t},t,\mathbf{h})=\frac{1}{\sqrt{1-\beta_{t}}}\left(\mathbf{x}_{t}- \frac{\beta_{t}}{\sqrt{1-\bar{\alpha}_{t}}} \epsilon_{\theta}(\mathbf{x}_{t}, \sqrt{\bar{\alpha}_{t}},\mathbf{h})\right)+\sqrt{\beta_{t}}\mathbf{n}$
    - $\mathbf{n}$ : Gaussian noise, $T$ : time step
    - 해당 DDPM sampling은 sampling step이 매우 크다는 한계가 있고, low-bitrate (1~1.5kbps)에서 over-smooth sample을 생성하고 phoneme missing이나 replacing 같은 hallucination effect가 나타나는 문제가 있음
  • 따라서 논문은 sampling 품질과 efficiency를 향상하기 위해 Midway-Infilling을 도입함
    1. 먼저 random noise space $\mathbf{x}_{T}$가 아닌 mid-point step $\tau < T$에서 sampling을 시작
       - 이를 통해 sampling 품질의 저하 없이 sampling step을 10~20배 줄일 수 있음
    2. 이후 sampling 중에 stronger conditioning을 수행하기 위해 separate conditioning branch를 적용
  • Midway-Infilling은 unconditional diffusion model에서 sampling step을 condition 하는 것을 목표로 하는 infilling algorithm을 기반으로 함
    
    1. 이를 위해 기존 infilling process에서는 occluded sample $\mathbf{s}_{0}$가 제공됨
    2. 그러면 diffusion process는 reversed sampling branch $\mathbf{x}_{t}$의 time step을 만족하기 위해 infilling branch $\mathbf{s}_{0}$에서 수행됨
       - 즉, $\mathbf{s}_{t}=\mathcal{F}(\mathbf{s}_{0},t)$
    3. $\mathbf{x}_{t}, \mathbf{s}_{t}$는 각 step에서 certain ratio로 interpolate 됨
  • 해당 infilling method와 비슷하게 midway-infilling 역시 2개의 branch를 활용함
    - BUT, $\mathbf{s}_{0}$ 대신 infilling branch의 Markov chain path에 대한 midway variable인 condition $\mathbf{h}$나 해당 upsampled version을 사용하여 $\mathbf{s}_{\tau}$를 근사함
    - 결과적으로 infilling branch는 아래 [Algorithm 1]과 같이 step $\tau$에서 $0$까지 reverse process를 수행

Midway-Infilling Algorithm

3. Experiments

- Settings

• Dataset : LibriSpeech
• Comparisons : EnCodec, DAC

- Results

• Comparison with Other Codec
  • MUSHRA test 측면에서 LaDiffCodec은 가장 우수한 성능을 보임

MUSHRA test 결과

• Mel-spectrogram 측면에서 LaDiffCodec은 aliasing artifact가 나타나지 않음

Mel-Spectrogram 비교

• Hyperparameters of Midway-Infilling
  
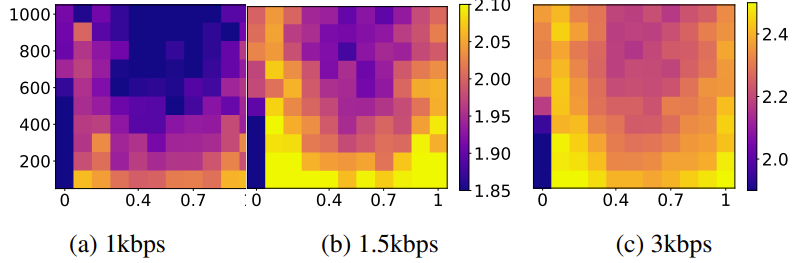
  • Midway-Infilling에서 $\gamma$가 작을수록 condition branch $[\mathbf{s}_{\tau},...,\mathbf{s}_{0}]$의 involvement가 적고 $\tau$가 클수록 sampling process는 더 많은 noise reduction을 수행함
    - $\gamma=0, \tau=1000$인 경우 DDPM의 sampling method와 동일
  • 이때 적절한 hyperparameter set를 선택하면 기존 DDPM sampling 보다 더 높은 PESQ를 달성할 수 있음
    - 결과적으로 sampling step $\tau$가 작고 $\gamma$가 0 또는 1에 가까울 때 최고의 품질을 달성 가능

Midway-Infilling Hyperparmeter 별 PESQ (X축 : mask ratio $\gamma$, Y축 : midway timestep $\tau$)

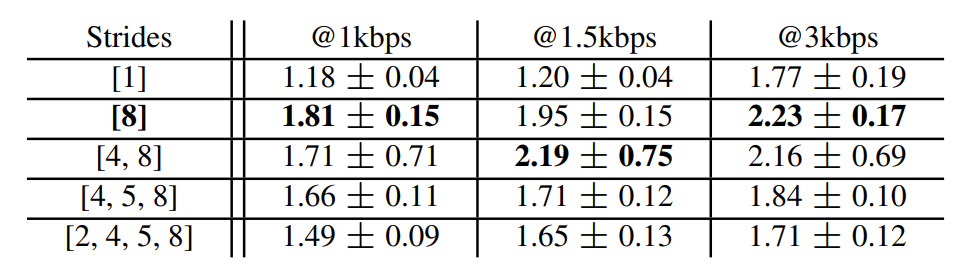
• Latent Dimensionality
  • Latent Diffusion model은 stride=1의 time-domain diffusion method 보다 좋은 성능을 보임
  • BUT, continuous autoencoder에 더 많은 sampling layer가 추가되면 expression power가 줄어듦

Latent Space Dimension 별 성능