[Paper 리뷰] DiffStyleTTS: Diffusion-based Hierarchical Prosody Modeling for Text-to-Speech with Diverse and Controllable Styles

DiffStyleTTS: Diffusion-based Hierarchical Prosody Modeling for Text-to-Speech with Diverse and Controllable Styles

---

• Rich, flexible prosodic variation을 위해서는 text-to-prosody의 one-to-many mapping 문제를 해결해야 함
• DiffStyleTTS
  • Conditional diffusion module과 classifier-free guidance를 활용
  • Speech prosodic feature를 hierarchically modeling 하고 다양한 prosodic style을 control
• 논문 (Coling 2025) : Paper Link

---

1. Introduction

• Text-to-Speech (TTS)의 naturalness와 prosodic performance는 acoustic model에 의해 결정됨
  • 특히 FastSpeech2와 같은 non-autoregressive acoustic model은 Gaussian distribution의 unimodal characteristic이 acoustic feature의 true distribution과 match 하지 않아 diversity가 떨어짐
    - 이를 위해 Global Style Token (GST)를 고려할 수 있지만 prosodic intensity를 control 하기 어려움
  • 한편 Diff-TTS, Grad-TTS, Guided-TTS와 같은 diffusion model은 multi-step sampling을 통해 over-smoothing prediction과 diversity 문제를 해결함
    - BUT, 여전히 prosody controllability와 transfer 측면에서는 한계가 있음

-> 그래서 prosodic feature를 더 효과적으로 control 할 수 있는 DiffStyleTTS를 제안

 

• DiffStyleTTS
  • Conditional diffusion module과 Classifier-Free Guidance를 통해 prosodic feature를 hierarchically modeling
  • 추가적으로 phoneme distortion 문제를 해결하기 위해 dynamic thresholding을 도입

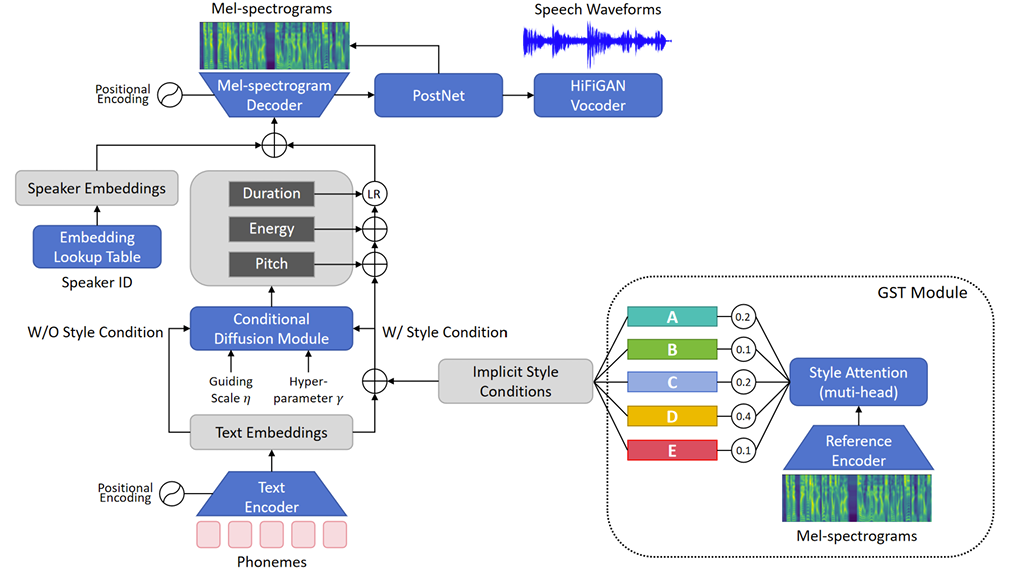
< Overall of DiffStyleTTS >

• Conditional diffusion과 Classifier-Free Guidance를 활용한 prosody controllable TTS model
• 결과적으로 기존보다 우수한 성능을 달성

2. Method

• DiffStyleTTS는 FastSpeech2를 backbone으로 사용함
  • 특히 encoder, decoder는 Feed-Forward Transformer (FFT)를 사용하고 decoder에는 5-layer convolutional PostNet이 추가됨
  • 각 speaker의 unique vocal characteristic을 capture 하기 위해 embedding lookup table을 사용하고 HiFi-GAN vocoder를 통해 waveform을 합성함
  • 추가적으로 variance adaptor를 hierarchical prosody modeling을 위한 Conditional Diffusion module로 replace 하고 style control을 위해 Global Style Token (GST) module을 도입함

- Hierarchical Prosody Modeling

• 논문은 hierarchical prosody modeling을 위해 coarse-grained implicit style condition과 fine-grained explicit prosodic description을 고려함
  • Implicit style condition은 entire sentence에 대한 broad description을 encompass 하고 mel-spectrogram으로부터 encoding 됨
    - Explicit prosodic feature는 pitch, energy, duration과 같은 speech waveform에서 추출되는 phoneme의 fine-grained prosodic description에 해당함
  • 특히 DiffStyleTTS는 GST를 따라 audio에서 implicit style condition을 추출함
    1. 추출된 implicit style condition은 global style token group에 해당하는 style vector로 decouple 됨
    2. Explicit prosodic feature의 경우 conditional diffusion module을 통해 predict 됨
       - 해당 module은 text embedding과 implicit style condition을 conditional term으로 사용함

Overview

- Conditional Diffusion Module

• Conditional diffusion module은 implicit style condition으로 guide 되어 해당 condition과 align 되는 explicit prosodic feature를 predict 함
  • 이때 guided generation을 위해 Classifier-Free Guidance를 활용할 수 있음
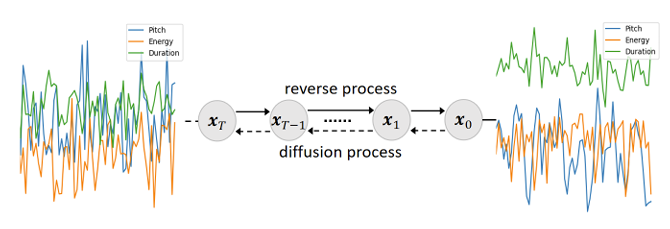
    1. 먼저 explicit prosodic feature의 diffusion process는 initial data $\mathbf{x}_{0}$에서 latent variable $\mathbf{x}_{t}$로의 fixed Markov chain으로 정의됨:
       (Eq. 1) $q(\mathbf{x}_{1:T}|\mathbf{x}_{0})=\prod_{t=1}^{T}q(\mathbf{x}_{t}|\mathbf{x}_{t-1})$
       (Eq. 2) $q(\mathbf{x}_{t}|\mathbf{x}_{t-1})=\mathcal{N}(\mathbf{x}_{t};\sqrt{1-\beta_{t}}\mathbf{x}_{t-1}, \beta_{t}I)$
       - $ \mathbf{x}_{t}=\sqrt{\bar{\alpha}_{t}}\mathbf{x}_{0}+\sqrt{1-\bar{\alpha}_{t}}\epsilon, \alpha_{t}=1-\beta_{t}, \bar{\alpha}_{t}=\prod_{s=1}^{t}\alpha_{s}$
       - $t=0,1,...,T$, $T$ : step size
    2. 각 step에서 small Gaussian noise를 add 할 때 module은 variance table에서 small positive constant $\beta_{t}$를 select 하고, 이는 Cosine schedule로 정의됨
    3. 그러면 reverse process는 $\mathbf{x}_{t}$에서 $\mathbf{x}_{0}$으로의 Markov chain으로 정의되고, $\theta$에 의해 parameterize 됨:
       (Eq. 3) $p_{\theta}(\mathbf{x}_{0:T})=p(\mathbf{x}_{T})\prod_{t=1}^{T}p_{\theta}(\mathbf{x}_{t-1}|\mathbf{x}_{t})$
       (Eq. 4) $p_{\theta}(\mathbf{x}_{t-1}|\mathbf{x}_{t})=\mathcal{N}(\mathbf{x}_{t-1};\mu_{\theta}(\mathbf{x}_{t},t),\sigma_{\theta}(\mathbf{x}_{t},t))$
       - 이는 isotropic Gaussian noise $\mathbf{x}_{T}\sim \mathcal{N}(0,I)$를 step-by-step denoising 하여 original data $\mathbf{x}_{0}$를 restore 하는 것으로 볼 수 있음
  • Conditional diffusion module output을 guide 하기 위해, text embedding $\mathbf{y}$를 condition으로 하여 phoneme을 explicit prosodic feature로 mapping 하는 2개의 denoiser를 도입함 
    1. Denoiser $\Psi_{\theta_{1}}(\mathbf{x}_{t},t,\mathbf{y},\mathbf{c})$는 $\mathbf{y},\mathbf{c}$를 conditional input으로 사용하고 denoiser $\Psi_{\theta_{2}}(\mathbf{x}_{t},t,\mathbf{y})$는 $\mathbf{y}$만 conditional input으로 사용함
    2. 각 denoising step에서 denoiser input은 noise $\epsilon\sim \mathcal{N}(0,I)$와 linearly combine 된 explicit prosodic feature $\mathbf{x}_{t}$로 구성됨
    3. 해당 noise를 modeling 하기 위해 2개의 denoiser는 다음의 objective로 training 됨:
       (Eq. 5) $\min_{\theta_{1}}\mathcal{L}_{diff\text{_}c}(\theta_{1})=\mathbb{E}_{\epsilon,\mathbf{x}_{t}, t,\mathbf{y},\mathbf{c}}|| \epsilon-\epsilon_{\theta_{1}}(\mathbf{x}_{t},t,\mathbf{y},\mathbf{c})||_{2}^{2}$
       (Eq. 6) $\min_{\theta_{2}}\mathcal{L}_{diff\text{_}nc}(\theta_{2})=\mathbb{E}_{\epsilon,\mathbf{x}_{t}, t,\mathbf{y}}|| \epsilon-\epsilon_{\theta_{2}}(\mathbf{x}_{t},t,\mathbf{y})||_{2}^{2}$
       - $\epsilon_{\theta_{1}}(\mathbf{x}_{t},t,\mathbf{y},\mathbf{c}),\epsilon_{\theta_{2}}(\mathbf{x}_{t},t,\mathbf{y})$ : noise output
    4. 추론 시 두 noise output은 linearly interpolate 됨:
       (Eq. 7) $\tilde{\epsilon}_{\theta_{1},\theta_{2}}(\mathbf{x}_{t},t,\mathbf{y},\mathbf{c})=\epsilon_{\theta_{2}}(\mathbf{x}_{t},t,\mathbf{y},\varnothing)+ \eta\left(\epsilon_{\theta_{1}}(\mathbf{x}_{t},t,\mathbf{y},\mathbf{c})-\epsilon_{\theta_{2}}( \mathbf{x}_{t},t,\mathbf{y},\varnothing)\right)$
       - $\eta$ : explicit prosodic feature의 diversity, quality를 balancing 하는 guidance intensity
  • 한편 $\eta\geq 7.0$인 경우 phoneme distrotion이 발생할 수 있음
    1. 이를 해결하기 위해 논문은 Dynamic Thresholding을 사용하여 각 sampling step에서 guidance result의 standard deviation을 correcting 함:
       (Eq. 8) $\sigma_{cond}=\text{std}\left(\epsilon_{\theta_{1}}(\mathbf{x}_{t},t,\mathbf{y},\mathbf{c})\right), \,\,\, \sigma_{cfg}=\text{std}\left(\tilde{\epsilon}_{\theta_{1},\theta_{2}}(\mathbf{x}_{t},t,\mathbf{y},\mathbf{c})\right)$
       (Eq. 9) $\tilde{\epsilon}_{rescaled}(\mathbf{x}_{t},t,\mathbf{y},\mathbf{c})=\tilde{\epsilon}_{\theta_{1},\theta_{2}}(\mathbf{x}_{t},t,\mathbf{y},\mathbf{c})\cdot\frac{\sigma_{cond}}{\sigma_{cfg}}$
       (Eq. 10) $\tilde{\epsilon}_{final}=\gamma\tilde{\epsilon}_{rescaled}(\mathbf{x}_{t},t,\mathbf{y},\mathbf{c})+(1-\gamma)\tilde{\epsilon}_{\theta_{1},\theta_{2}}(\mathbf{x}_{t},t,\mathbf{y},\mathbf{c})$
    2. 이는 $\tilde{\epsilon}_{\theta_{1},\theta_{2}}(\mathbf{x}_{t},t,\mathbf{y},\mathbf{c})$의 standard deviation을 $\epsilon_{\theta_{1}}(\mathbf{x}_{t},t,\mathbf{y},\mathbf{c})$의 original standard deviation으로 correct 함
       - Correction scale $\gamma$는 final corrected result $\tilde{\epsilon}_{final}$의 correction intensity를 adjust 함
  • 결과적으로 conditional diffusion module은 implicit style condition $\mathbf{c}$를 사용하여 explicit prosodic feature generation을 guide 함
    - 추가적으로 guding scale $\eta$와 correction scale $\gamma$를 통해 diversity와 guidance intensity를 adjust 함

Diffusion/Reverse Process

- Training

• Text analysis front-end의 processed phoneme은 Text Encoder로 전달되어 text embedding을 생성함
  • 이후 GST module의 implicit style condition과 함께 conditional diffusion module에 input 됨
    - 해당 module은 (Eq. 5), (Eq. 6)을 통해 training 된 2개의 denoiser $\Psi_{\theta_{1}}(\mathbf{x}_{t},t,\mathbf{y},\mathbf{c}), \Psi_{\theta_{2}}(\mathbf{x}_{t},t,\mathbf{y})$로 구성됨
  • Training 시에는 log-scale raw phoneme-wise pitch/duration, raw phoneme-wise energy가 sampling target으로 사용되고, guiding scale $\eta$와 correction scale $\gamma$는 involve 하지 않음
    1. Implicit style condition과 raw pitch/energy embedding을 text embedding에 add 한 다음 Length Regulator를 사용하여 raw duration과 align 함
       - Frame-wise speaker embedding은 decoder 이전에 add 됨
    2. 최종적으로 decoded mel-spectrogram은 pre-trained HiFi-GAN을 통해 waveform으로 convert 됨
  • Total loss는 diffusion module loss, mel-spectrogram decoding loss, PostNet의 resdiual loss로 구성됨:
    (Eq. 11) $\mathcal{L}_{total}=\mathcal{L}_{diff\text{_}c}(\theta_{1})+\mathcal{L}_{diff\text{_}nc}(\theta_{2})+\mathcal{L}_{decoder}+\mathcal{L}_{mel}$

Training/Inference

- Inference

• DiffStyleTTS는 다음 3가지의 inference mode를 고려함
  • Diversified Controllable Inference
    
    1. Guiding scale $\eta$, correction scale $\gamma$를 tuning 하여 diversity와 explicit prosodic feature의 guidance intensity를 adjust 할 수 있음
    2. 이를 통해 diversified, controllable prosody prediction이 가능함
  • Prosodic Transfer Inference
    1. Specified speaker ID가 주어지면 prosodic feature를 해당 speaker로 transfer 할 수 있음
    2. 이때 $\eta, \gamma$를 tuning 하여 prosodic transfer intensity를 adjust 함
  • Prosodic Control Inference
    1. Specified speaker ID와 GST module의 token ID가 주어지면 다른 token weight를 $0$, 해당 token weight는 $1$로 설정하여 GST token에 대해서만 control 되는 prosody를 얻을 수 있음
    2. 특히 scaling factor를 multiply 하여 pitch, energy, duration을 scale 해 prosodic value를 control 함
  • 추가적으로 논문은 terminal condition $\mathbf{x}_{T}$를 $\mathcal{N}(0,I)$가 아닌 $\mathcal{N}(0,\tau^{-1}I)$에서 sample 하기 위해 temperature hyperparameter $\tau$를 도입함

3. Experiments

- Settings

• Dataset : Mandarin dataset (internal)
• Comparisons : FastSpeech2, Grad-TTS, Guided-TTS, DiffProsody

- Results

• 전체적으로 DiffStyleTTS의 성능이 가장 우수함

Model 성능 비교

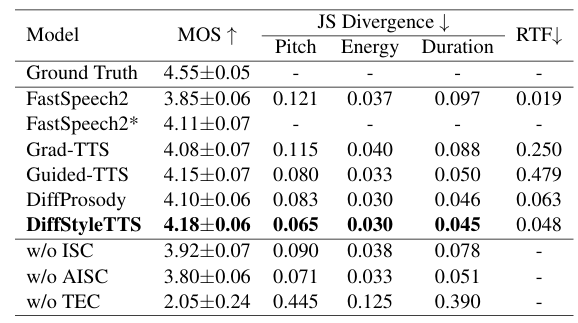
• Prosodic Control
  • $\eta=1.0, \gamma=0.7$에서 최적의 성능을 보임

Guidance Scale 별 성능

• $\eta=7.0$을 사용하면 phoneme distrotion이 나타나는데 $\gamma$를 활용하여 이를 alleviate 할 수 있음

Spectrogram 비교 (상) $\gamma=0$ (중) $\gamma=0.4$ (하) $\gamma=0.7$

• $t$-SNE 측면에서도 prosody 별 cluster를 확인할 수 있음

$t$-SNE

• Prosodic Transfer
  • Prosodic transfer 측면에서도 DiffStyleTTS가 가장 선호됨

Prosodic Transfer

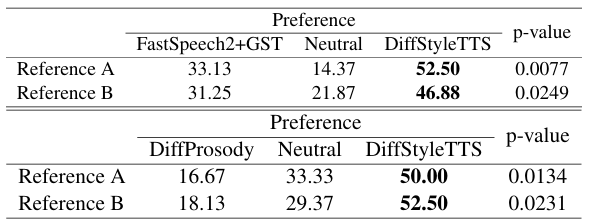
• $\eta$가 증가할수록 prosodic transfer는 더 pronounce 해짐

$\eta$의 영향