[Paper 리뷰] SSAMBA: Self-Supervised Audio Representation Learning with Mamba State Space Model

SSAMBA: Self-Supervised Audio Representation Learning with Mamba State Space Model

---

• Audio representation learning을 위한 Transformer architecture는 memory, inference time 측면에서 quadratic complexity를 가짐
• SSAMBA
  • State Space Model인 Mamba를 self-supervised audio representation learning에 도입
  • Bidirectional Mamba를 사용하여 complex audio pattern을 capture 하고 unlabeled dataset으로부터 robust audio representation을 학습
• 논문 (SLT 2024) : Paper Link

---

1. Introduction

• Robust audio representation learning을 위해서는 short/long-range dependency를 모두 capture 해야 함
  • 특히 SSAST와 같은 Self-Supervised Learning (SSL) 기반의 Audio Spectrogram Transformer (AST)는 audio downstream task에서 우수한 성능을 달성함
    - BUT, Transformer architecture는 quadratic computation과 memory usage로 인한 한계가 있음
  • 이와 달리 State Space Model (SSM)은 Transformer와 마찬가지로 strong sequence modeling이 가능하지만 sub-quadratic complexity를 가진다는 장점이 있음

-> 그래서 Mamba를 활용한 audio representation learning model인 SSAMBA를 제안

 

• SSAMBA
  • Audio spectrogram을 patch로 split 한 다음, bidirectional Mamba encoder에 input 하여 selective state space를 통해 global audio context를 capture
  • Large unlabeled dataset에서 masked spectrogram patch를 통해 self-supervised learning을 수행

< Overall of SSAMBA >

• Mamba와 Self-Supervised Learning을 활용한 audio representation model
• 결과적으로 다양한 downstream task에서 우수한 성능을 달성

2. Method

- Mathematical Foundations of the Mamba Model

• State Space Model (SSM)은 1-dimensional function이나 sequence $x(t)\in\mathbb{R}$을 hidden state $h(t)\in\mathbb{R}^{N}$을 통해 output $y(t)\in\mathbb{R}$로 mapping 함
  • 해당 sequence modeling framework는 evolution parameter $A\in\mathbb{R}^{N\times N}$, projection parameter $B\in \mathbb{R}^{N\times 1}, C\in \mathbb{R}^{1\times N}$을 기반으로 동작함
  • 먼저 continuous-time SSM은 다음의 differential equation으로 정의됨:
    (Eq. 1) $h'(t)=Ah(t)+Bx(t)$
    (Eq. 2) $y(t)=Ch(t)$
  • Discretized SSM에서는 timescale parameter $\Delta$와 Zero-Order Hold (ZOH) method를 사용하여 continuous parameter $A,B$를 discrete parameter로 transform 함:
    (Eq. 3) $A_{d}=\exp(\Delta A)$
    (Eq. 4) $B_{d}=(\Delta A)^{-1}(\exp(\Delta A)-I)\cdot \Delta B$
  • Discretization 이후, step size $\Delta$의 discrete-time signal에 대한 SSM은:
    (Eq. 5) $h_{t}=A_{d}h_{t-1}+B_{d}x_{t}$
    (Eq. 6) $y_{t}=Ch_{t}$
  • Output sequence $y_{t}$를 efficiently compute 하기 위해 global convolution operation을 사용할 수 있음
    1. 즉, output $y$는 input sequence $x$를 structured convolutional kernel $K_{d}$와 convolve 하여 얻어짐
    2. 해당 kernel은 matrix $A_{d}, B_{d}, C$로부터 pre-compute 됨:
       (Eq. 7) $K_{d}=(CB_{d},CA_{d}B_{d},...,CA_{d}^{M-1}B_{d})$
       (Eq. 8) $y=x*K_{d}$
       - $M$ : input sequence $x$ length, $K\in \mathbb{R}^{M}$ : structured convolutional kernel
  • 여기서 Mamba는 각 timestep $t$에서 input $x_{t}$를 기반으로 parameter $\Delta_{t}, A_{t},B_{t},C_{t}$에 대한 dynamic update를 incorporate 하여 앞선 SSM framework를 개선함
    
    1. 이를 통해 input-selective, content-aware 하게 만들어 input sequence의 specific characteristic에 dynamically adjust 할 수 있도록 함
    2. 특히 Mamba는 dynamic update를 위해 convolution을 dynamically recalculate 하는 selective-scan algorithm을 도입함

Overview

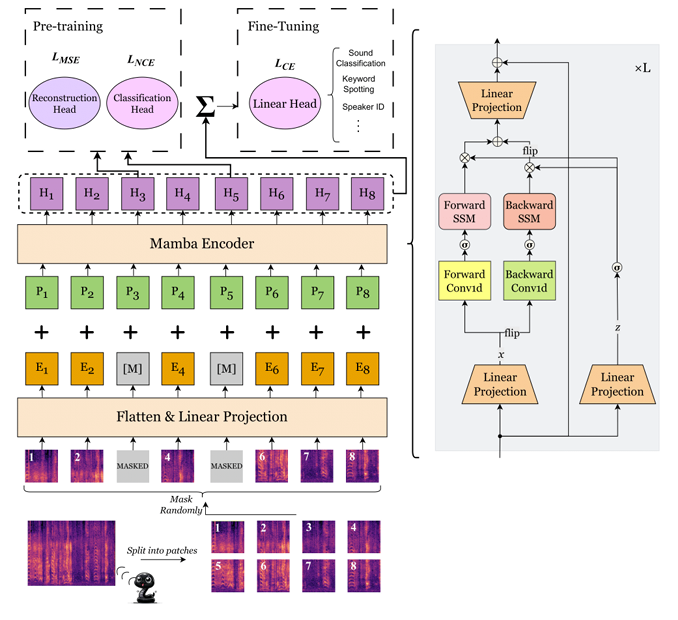
- SSAMBA Architecture

• Spectrogram Input Representation
  • Input audio waveform은 audio data의 time-frequency domain을 represent 하는 spectrogram으로 변환됨
    1. 이를 위해 논문은 25ms Hanning window와 10ms 마다 STFT를 적용하여 128-dimensional log mel-filterbank feature를 compute 함
    2. 결과적으로 spectrogram matrix $S$는 $128\times 100t$ dimension을 가짐
       - $F=128$ : frequency bin 수, $T=100t$ : $t$-second audio length에 대한 time frame 수
  • 이후 논문은 해당 spectrogram을 $16\times 16$ patch로 split 함
    - e.g.) 10s audio input을 $16\times 16$ patch와 16 stride로 divide 하면 500 patch를 얻을 수 있음
• Flatten and Linear Projection
  • 각 spectrogram patch $S_{i}$는 1D vector로 flatten 된 다음 linear projection layer를 통해 higher-dimensional space로 project 됨
  • 이를 통해 dimension $D$의 embedding $E_{i}$를 얻을 수 있음
• Positional Encoding
  • Spectrogram patch의 temporal order와 spatial structure를 capture 하기 위해, patch embedding $E_{i}$와 동일한 dimension $D$를 가지는 learnable positional encoding $P_{i}$가 add 됨
  • Positional encoding은 model이 spectrogram 내의 각 patch에 대한 positional information을 retain 하도록 함
• Mamba Encoder
  • SSAMBA는 bidirectional SSM으로 구성된 Mamba encoder를 사용함
    - Mamba encoder는 combined embedding $E_{i}+P_{i}$를 처리하여 forward/backward dependency를 capture 함
  • $M$을 input sequence의 patch 수, $z$를 SSM block의 forward/backward output을 modulate 하는 intermediate representation이라고 했을 때, bidirectional modeling은 [Algorithm 1]과 같이 정의됨

Bidirectional Mamba Block Processing

- Self-Supervised Learning Framework

• SSAMBA는 discriminative, generative objective를 jointily optimize 하여 robust audio representation을 학습함
• Masked Spectrogram Patches
  • 먼저 spectrogram $S$는 non-overlapping patch sequence로 split 됨
    - 각 patch $S_{i}$의 size는 $F_{p}\times T_{p}$과 같고, $F_{p}, T_{p}$는 각각 frequency, time domain의 dimension에 해당함
  • Pre-training 시 해당 patch의 일부는 randomly mask 됨
    - Masked patch embedding $[M]$은 model의 predict target으로 사용되어 model이 audio data의 underlying structure를 학습하도록 함
• Training Obejctive
  • SSAMBA의 training objective는 discriminative, generative task를 integrate 하여 구성됨
  • Discriminative Objective
    1. Discriminative objective는 masked patch를 correctly identifying 하는 것을 목표로 함
    2. Discriminative task는 각 masked patch에 대한 vector를 output 하는 classification head를 사용해 output vector와 다른 모든 embedding 간의 InfoNCE loss를 compute 함:
       (Eq. 9) $ \mathcal{L}_{d}=-\frac{1}{N}\sum_{i=1}^{N}\log \left(\frac{\exp\left( \langle c_{i},x_{i}\rangle\right)}{\sum_{j=1}^{N}\exp\left( \langle c_{i},x_{j}\rangle \right)}\right)$
       - $c_{i}$ : $i$-th masked patch에 대한 classification head output
       - $x_{i}$ : $i$-th patch의 actual embedding, $N$ : total patch 수
  • Generative Objective
    • Generative objective는 masked patch의 original content를 reconstruct 하는 것을 목표로 함
    • 이때 reconstruction head는 masked embedding에 대한 prediction을 생성하고, Mean Squared Error (MSE)를 통해 evaluate 됨:
      (Eq. 10) $\mathcal{L}_{g}=\frac{1}{N}\sum_{i=1}^{N}\left|\left| \hat{x}_{i}-x_{i}\right|\right|^{2}$
      - $\hat{x}_{i}$ : masked patch의 predicted reconstruction, $x_{i}$ : patch의 true embedding
  • 결과적으로 total loss $\mathcal{L}$은 discriminative, generative loss의 weighted sum으로 얻어짐:
    (Eq. 11) $\mathcal{L}=\mathcal{L}_{d}+\lambda \mathcal{L}_{g}$
    - $\lambda$ : balancing parameter

3. Experiments

- Settings

• Dataset
  - Pre-training : AudioSet, LibriSpeech
  - Downstream Task : AudioSet (AS), ESC, Speech Commands 1 (KS1), Speech Commands 2 (KS2), VoxCeleb (SID), IEMOCAP (ER), Urban8K Sound (DASL)
• Comparisons : APC, Wav2Vec, Wav2Vec 2.0, HuBERT, SSAST

Model Specification

- Results

• 전체적으로 SSAMBA의 성능이 가장 우수함

Model 성능 비교

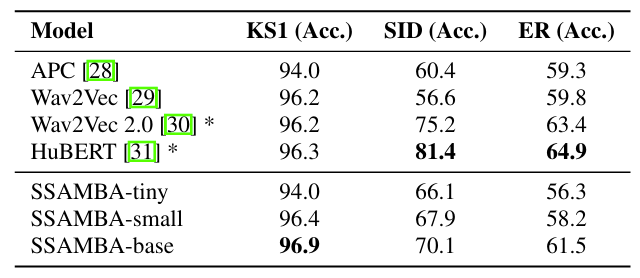
• 각 downstream task에서 SSAST와 비교하여 더 나은 성능을 달성함

SSAST와의 비교

• SSAMBA는 SSAST와 비교하여 $92.7\%$ 더 빠른 추론 속도와 $95.4\%$의 memory efficiency를 가짐

Efficiency 비교

• Ablation Study
  • 400 masked patch를 사용하는 경우 최적의 성능을 달성할 수 있음

Ablation Study