[Paper 리뷰] HuBERT-VIC: Improving Noise-Robust Automatic Speech Recognition of Speech Foundation Model via Variance-Invariance-Covariance Regularization

HuBERT-VIC: Improving Noise-Robust Automatic Speech Recognition of Speech Foundation Model via Variance-Invariance-Covariance Regularization

---

• Speech foundation model은 noise-robustness 측면에서 한계가 있음
• HuBERT-VIC
  • Variance, Invariance, Covariance regularization objective를 활용하여 model을 training
  • Noisy speech representation의 statistics를 adjust 하여 다양한 noise type에 대한 generalization ability를 향상
• 논문 (INTERSPEECH 2025) : Paper Link

---

1. Introduction

• Wav2Vec 2.0, Data2Vec 등의 Speech Foundation Model (SFM)은 Automatic Speech Recognition (ASR)과 같은 다양한 downstream task에서 우수한 성능을 보이고 있음
  • 대표적으로 HuBERT는 large-scale unlabeled speech data를 활용하여 annotated data에 대한 의존성을 줄이고, masked codeword frame을 predict 하여 complex acoustic pattern을 capture 함
    - BUT, 해당 model은 clean speech로 training 되므로 noisy real-world data에 대해서는 성능 저하를 보임
  • 이를 해결하기 위해 Wav2Vec-Switch, Robust Data2Vec, HuBERT-AGG 등과 같이 noise-robustness를 향상하는 방법들을 고려할 수 있음
    1. BUT, 해당 방식들은 feature channel dimension의 variability를 control 하는 explicit regularization이 없는 joint embedding을 활용하므로 representation collapse 문제가 나타남
    2. 추가적으로 contrastive loss를 주로 활용하므로 high-resource가 요구됨

-> 따라서 noise-robust SFM을 위해 feature-level statistics를 effectively control하는 HuBERT-VIC를 제안

 

• HuBERT-VIC
  • Variance-Invariance-Covariance Regularization (VICReg)-based loss를 활용하여 noisy speech representation의 statistics를 control
  • VICReg term의 decorrelation을 통해 다양한 speech characteristic을 capture 하도록 지원

< Overall of HuBERT-VIC >

• VICReg term을 활용한 noisy-robust speech representation model
• 결과적으로 기존보다 우수한 성능을 달성

2. Method

- HuBERT

• HuBERT는 masked prediction task를 활용하는 SFM으로써 input sequence의 segment를 mask 하고 해당 hidden unit codeword를 predict 함
  • 구조적으로 HuBERT는 CNN feature encoder와 consecutive Transformer layer로 구성됨
  • CNN feature extractor에서 masked timestep $M$에 대한 masked representation $\mathbf{X}=[\mathbf{x}_{1},\mathbf{x}_{2},...,\mathbf{x}_{T}]$가 주어졌을 때, masked prediction objective는:
    (Eq. 1) $\mathcal{L}_{m}(\mathbf{X})=\sum_{t\in M}\log p(\mathbf{c}_{t}|\mathbf{X},t)$
    - $\mathbf{C}=[\mathbf{c}_{1},\mathbf{c}_{2},...,\mathbf{c}_{T}]$ : $C$ codeword candidate에 대한 $T$ timestep의 probability distribution 

Overview

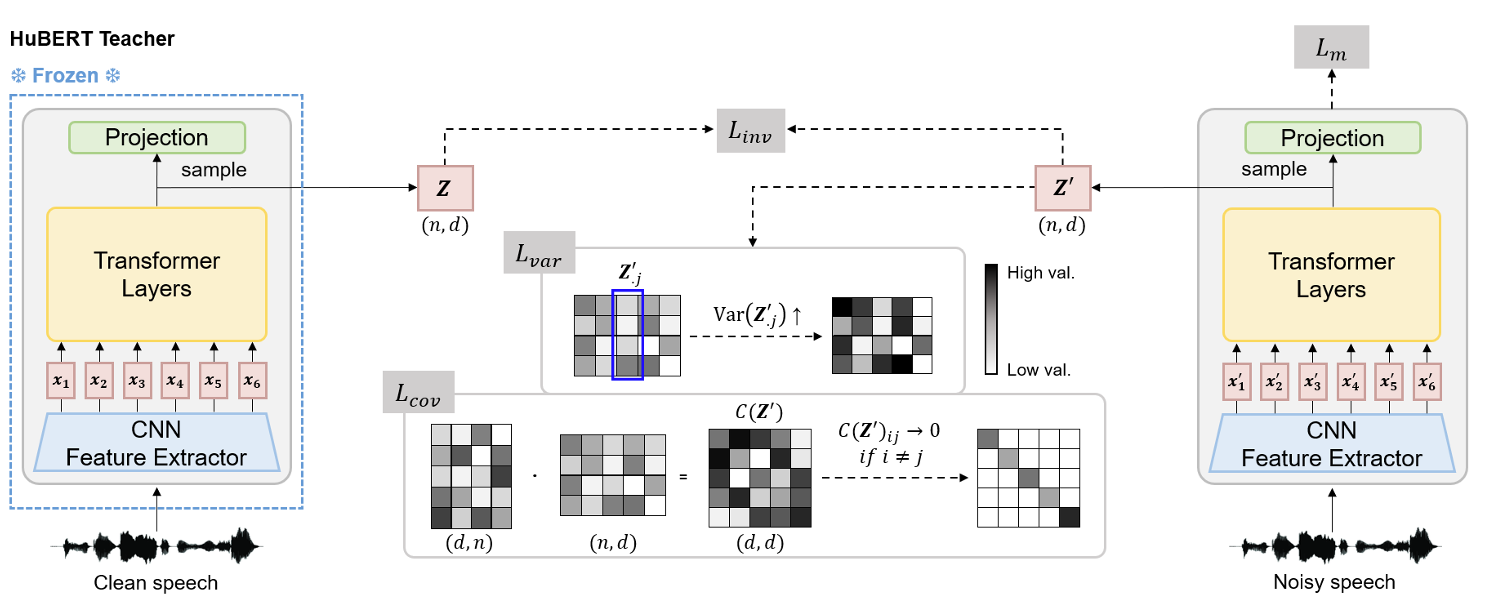
- HuBERT-VIC

• Speech representation의 robustness를 향상하기 위해 논문은 Variance, Invariance, Covariance regularization term을 도입함
  • 해당 regularization term을 incorporate 함으로써 speech repersentation의 sufficient variance를 maintain 하고, noise의 invariance를 enforce 하고, specific noise characteristic에 대한 overfitting을 방지함
    - 결과적으로 이를 통해 model의 noise-robustness와 generalization ability를 향상함
  • HuBERT-VIC의 training pipeline에서 teacher model은 clean speech로 pre-training 되고, noise-robust pre-training 시에는 freeze 됨
    1. Student model의 경우 teacher와 동일한 clean pre-trained weight로 initialize 되고, noise-augmented speech input으로 training 됨
    2. 여기서 논문은 teacher, student model의 final Transformer layer output에서 time-axis를 따라 $n$ time frame을 sampling 함
       - 해당 frame은 batch 내의 multiple utterance에서 randomly select 됨
  • Channel dimension $d$에 대해 teacher, student의 sampled representation을 $\mathbf{Z},\mathbf{Z}'\in\mathbb{R}^{n\times d}$라고 하자
    - 그러면 해당 representation은 $\mathbf{Z}=[\mathbf{z}_{1},\mathbf{z}_{2},...,\mathbf{z}_{n}],\mathbf{Z}'=[\mathbf{z}'_{1},\mathbf{z}'_{2},...,\mathbf{z}'_{n}]$으로 나타낼 수 있음
• Invariance Term
  • Sampled representation $\mathbf{Z},\mathbf{Z}'$이 주어졌을 때, invariance regularization term은 clean teacher representation과 nosiy student counterpart 간의 discrepancy를 minimize 함
    - 이를 통해 model은 noisy representation에 대해서도 consistency를 maintain 할 수 있음
  • 이때 invariance term은 Mean Squared Error (MSE)를 통해 얻어짐:
    (Eq. 2) $ s(\mathbf{Z},\mathbf{Z}')=\frac{1}{n}\sum_{i=1}^{n}\left|\left| \mathbf{z}_{i}-\mathbf{z}'_{i}\right|\right|_{2}^{2}$
• Variance Term
  • Variance regularization은 $\mathbf{Z}'$의 channel dimension에 대한 sufficient dispersion을 보장하고, learned representation이 certain dimension에 overly concentrate 되는 representation collapse를 방지함
  • $j$-th column vector $\mathbf{Z}'_{\cdot j}=[Z'_{1j},Z'_{2j},...,Z'_{nj}]^{\top}$에 대해, variance term은:
    (Eq. 3) $v(\mathbf{Z}')=\frac{1}{d}\sum_{j=1}^{d}\max\left(0,\gamma-\sqrt{\text{Var}(\mathbf{Z}'_{\cdot j})+\epsilon}\right)$
    - 각 channel dimension은 hyperparameter $\gamma$를 사용한 hinge loss를 통해 minimum variability를 maintain 하고, small scalar $\epsilon$은 numerical instability를 방지하기 위해 사용됨
  • Variance term은 channel dimension 간 information의 balanced dsitribution을 보장하고 noise-robustness를 위해 다양한 acoustic characteristic을 capture 하도록 함
    1. 특히 channel level high variance는 model이 noisy speech를 better handling 할 수 있도록 함
    2. 추가적으로 clean/noisy representation 간의 차이를 학습하는 invariance term을 complement 함
• Covariance Term
  • Covariance regularization은 각 channel dimension이 distinct, independent information을 capture 할 수 있도록 channel dimension pair 간의 redundancy를 줄이는 것을 목표로 함
    1. 이를 위해 noise-perturbed representation의 covariance matrix가 $C(\mathbf{Z}')\in\mathbb{R}^{d\times d}$는 channel dimension 간의 relationship을 capture 하기 위해 calculate 됨
    2. 이후 $C(\mathbf{Z}')$의 off-diagonal element는 $c(\mathbf{Z}')$으로 penalize 되어 $0$으로 pushing 됨:
       (Eq. 4) $C(\mathbf{Z}')=\frac{1}{n-1}\sum_{i=1}^{n}(\mathbf{z}'_{i}-\bar{\mathbf{z}}'_{i})^{\top} (\mathbf{z}'_{i}-\bar{\mathbf{z}}'),\,\,\, \bar{\mathbf{z}}'=\frac{1}{n}\sum_{i=1}^{n}\mathbf{z}'_{i}$
       (Eq. 5) $c(\mathbf{Z}')=\frac{1}{d}\sum_{i\neq j}\left|\left| C(\mathbf{Z}')_{ij}\right|\right|^{2}_{2}$
  • Covariance term은 channel dimension 간의 redundancy를 줄여 noise-robustness를 향상함
  • 결과적으로 3개의 regularization term을 combine 하여 얻어지는 VIC loss는:
    (Eq. 6) $\mathcal{L}_{VIC}=\lambda s(\mathbf{Z},\mathbf{Z}')+\mu v(\mathbf{Z}')+\nu c(\mathbf{Z}')$
    (Eq. 7) $\mathcal{L}_{tot}=\mathcal{L}_{m}+\alpha\mathcal{L}_{VIC}$
    - Combined final objective $\mathcal{L}_{tot}$는 regularization loss $\mathcal{L}_{VIC}$와 masked prediction loss $\mathcal{L}_{m}$으로 구성됨

3. Experiments

- Settings

• Dataset : LibriSpeech + MUSAN
• Comparisons : HuBERT, HuBERT-AGG

- Results

• 전체적으로 HuBERT-VIC의 성능이 가장 뛰어남

Model 성능 비교

• Noisy speech에 대해서도 우수한 성능을 보임

Noisy Speech에서의 성능

• Ablation Study
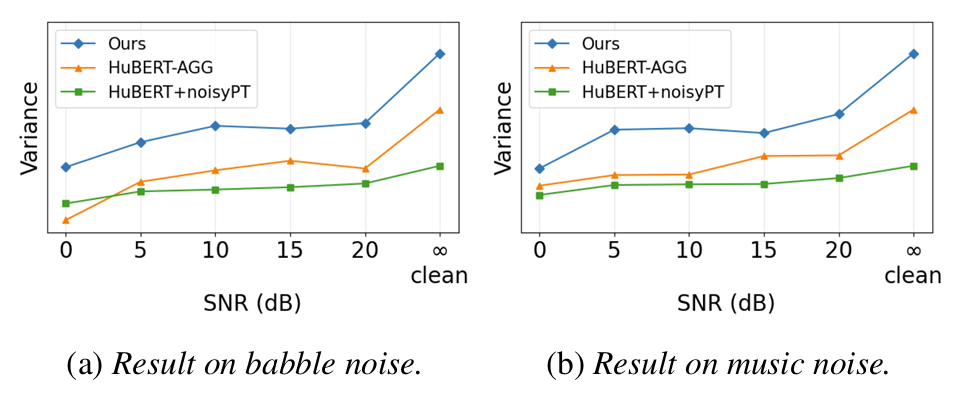
  • 각 regularization term을 추가할수록 더 나은 성능을 얻을 수 있음

Regularization Term의 효과

• Input speech의 high SNR은 higher variance로 이어짐

SNR과 Variance Term의 관계