[Paper 리뷰] AxLSTMs: Learning Self-Supervised Audio Representations with xLSTMs

AxLSTMs: Learning Self-Supervised Audio Representations with xLSTMs

---

• xLSTM은 Transformer와 비교할만한 성능을 가짐
• AxLSTM
  • Self-supervised setting에서 xLSTM을 활용해 masked spectrogram patch로부터 general-purpose audio representation을 학습
  • AudioSet dataset으로 pre-training 하여 다양한 downstream task에 대응
• 논문 (INTERSPEECH 2025) : Paper Link

---

1. Introduction

• Transformer는 뛰어난 generalization ability와 data-agnostic nature를 가지지만 scaled dot-product로 인한 complexity의 한계가 있음
  • 한편 Transformer 이전의 Recurrent Neural Network (RNN) 역시 sequence modeling에 효과적임
    - RNN은 sequence length에 대해 linearly scale 되고 entire key-value (KV) cache를 store 할 필요가 없으므로 runtime memory requirement가 낮다는 장점이 있음
  • BUT, 대표적인 RNN approach인 LSTM은 다음의 문제점을 가지고 있음:
    1. Storage decision을 revise 할 수 없음
    2. Information을 scalar cell state로 compressing 하므로 rare input token에 영향을 미침
    3. Memory mixing으로 인해 parallelizing이 어려움
  • 이때 xLSTM을 활용하면 이러한 LSTM의 단점들을 해결할 수 있음

-> 그래서 xLSTM을 audio self-supervised learning에 적용한 AxLSTM을 제안

 

• AxLSTM
  • xLSTM을 기반으로 spectrogram patch로부터 masked modeling framework를 적용
  • AudioSet에 대한 pre-training을 수행하여 다양한 downstream task에 대한 성능을 향상

< Overall of AxLSTM >

• xLSTM architecture와 self-supervised learning을 활용한 general-purpose audio representation model
• 결과적으로 다양한 audio downstream task에서 우수한 성능을 달성

2. Method

- Prerequisites: xLSTM and mLSTM Block

• xLSTM은 sLSTM, mLSTM의 2가지 building block으로 구성되고, 논문은 mLSTM을 fundamental building block으로 채택함
  • 먼저 parallelizable mLSTM block은 matrix memory cell $C\in \mathbb{R}^{d\times d}$를 사용하여 original LSTM cell을 개선함:
    1. mLSTM은 timestep $t$에서 $k_{t},v_{t}\in\mathbb{R}^{d}$의 key-value vector pair를 store 하고 relevant value vector는 query $q_{t+\tau}\in\mathbb{R}^{d}$를 통해 retrieve 됨
       
    2. 즉, mLSTM의 forward pass는:
       (Eq. 1) $ C_{t}=f_{t}C_{t-1}+i_{t}v_{t}k^{\top}_{t}$
       (Eq. 2) $n_{t}=f_{t}n_{t-1}+i_{t}k_{t}$
       (Eq. 3) $h_{t}=o_{t}\odot C_{t}q_{t}/\max\left\{|n_{t}^{\top}q_{t}|,1\right\}$
       (Eq. 4) $q_{t}=W_{q}x_{t}+b_{q}$
       (Eq. 5) $k_{t}=\frac{1}{\sqrt{d}}W_{k}x_{t}+b_{k}$
       (Eq. 6) $v_{t}=W_{v}x_{t}+b_{v}$
       (Eq. 7) $i_{t}=\exp\left(w^{\top}_{i}x_{t}+b_{i}\right)$
       (Eq. 8) $f_{t}=\exp\left(w_{f}^{\top}x_{t}+b_{f}\right)$
       (Eq. 9) $o_{t}=\sigma(W_{o}x_{t}+b_{o})$
       - $C_{t}$ : matrix memory cell, $h_{t}$ : normalizer state/hidden state, $i_{t}, f_{t},o_{t}$ : 각각 input/forget/ouput gate
       - $W_{q},W_{k},W_{v}$ : weight로써 각각 query $q$, key $k$, value $v$에 대한 learnable projection matrix
  • mLSTM에는 memory mixing이 없으므로 multiple memory cell과 multiple head는 equivalent 하고 forward pass는 parallelize 될 수 있음
    - 추가적으로 mLSTM에는 storage decision을 revise 하기 위한 exponential gating이 적용됨

Overview

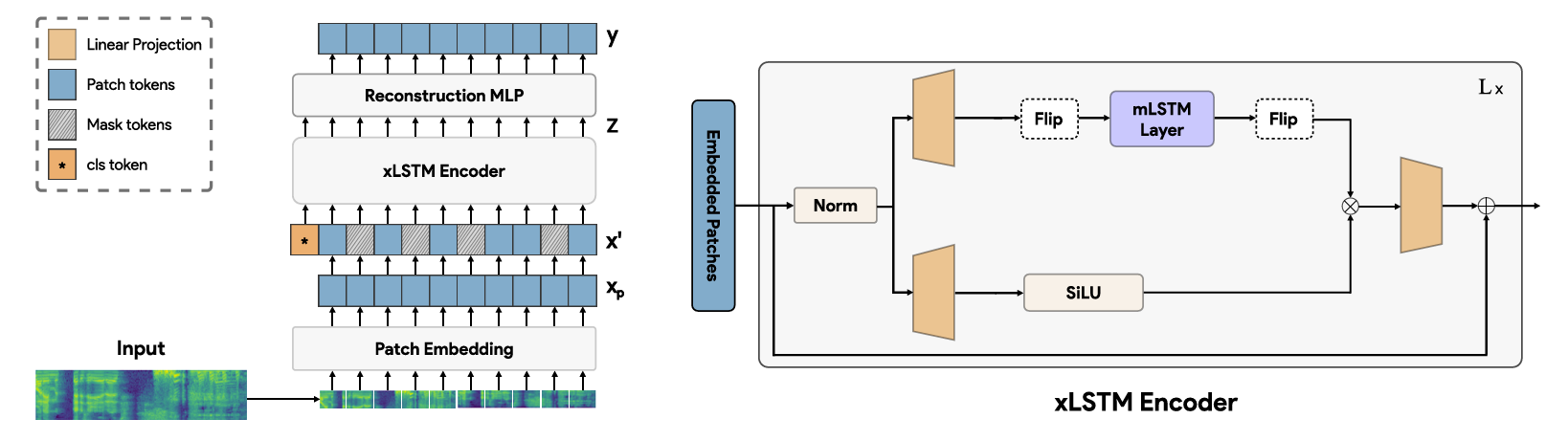
- AxLSTM: Modeling Masked Patches with xLSTMs

• Creating and Masking Patches
  • Input spectrogram $\mathbf{x}\in\mathbb{R}^{T\times F}$가 주어지면, shape $\times f$의 non-overlapping patch를 compute 하여 $\mathbf{x}_{p}\in\mathbb{R}^{N\times (t\cdot f)}$ patch를 생성함
  • 다음으로 patch는 $\mathbb{R}^{N\times d_{m}}$ dimensional space에 project 되고, fixed sinusoidal 2D positional embedding이 add 됨
    - 이때 representative class token이 sequence beginning에 add 되어 fine-tuning을 지원함
  • 이후 input patch의 $50\%$를 randomly mask 하고 해당 masked patch를 learnable mask token으로 replace 함
  • 즉, encoder input은:
    (Eq. 10) $ \mathbf{x}'=\left[\text{cls},\mathbf{x}_{p}^{1},\mathbf{x}_{p}^{2},...,\mathbf{x}_{p}^{N}\right] +E_{pos}$ 
• Encoding and Reconstruction
  • Partially masked patch는 encoder에 전달되어 encoded representation $\mathbf{z}=\text{enc}(\mathbf{x}'), \mathbf{z}\in\mathbb{R}^{(N+1)\times d_{m}}$을 yield 함
  • 구조적으로 encoder는 mLSTM block stack으로 구성되고, 각 block은 $d_{m}$ dimensional input을 expansion factor $E_{f}$로 expand 한 다음, $d_{m}$으로 다시 project 함
    - 이로 인해 resulting block은 Transformer block 보다 더 적은 parameter를 가짐
  • 추가적으로 input의 bidirectional modeling을 위해 input sequence order를 reverse 하는 $\text{flip}$ operation을 짝수 mLSTM block에 적용할 수 있음
    
  • Encoding 이후에는 single hidden layer가 encoded representation $\mathbf{z}$로부터 patch를 reconstruct 하는 데 사용됨:
    (Eq. 11) $\mathbf{y}'=\text{Linear}_{(t\cdot f)}\left(\sigma(\text{Linear}_{d_{m}}(\mathbf{z}))\right)$
    - $\text{Linear}_{d}$ : dimension $d$의 parameterized linear projection
    - $\sigma$ : GELU non-linear activation
  • 최종적으로 original input spectrogram과 reconstruction 간의 Mean Squared Error (MSE)는 masked patch에 대해서만 compute 되어 pre-training을 위한 loss로 사용됨

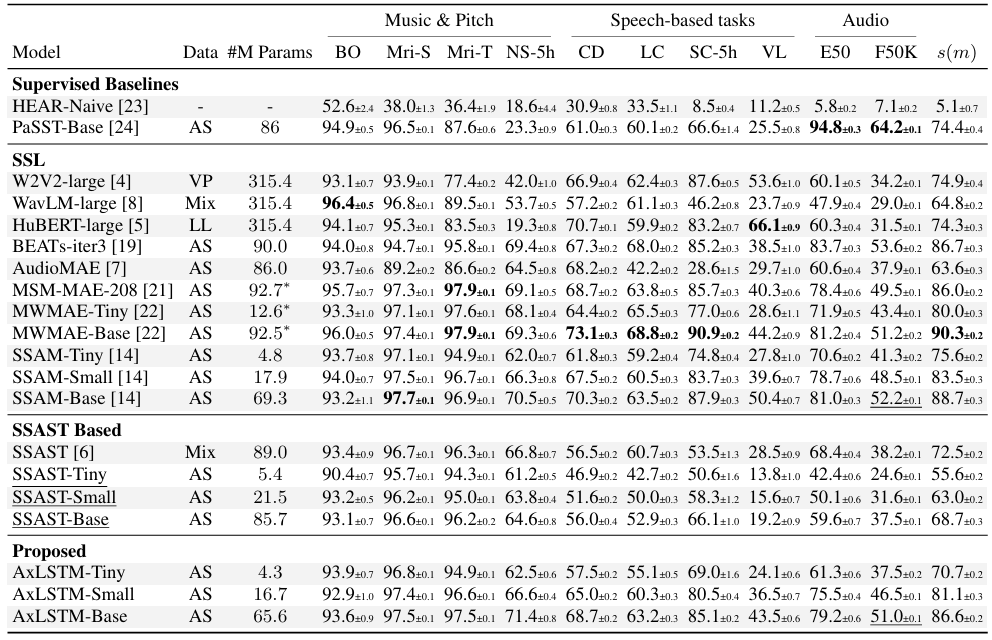
3. Experiments

- Settings

• Dataset : AudioSet
• Comparisons : Wav2Vec 2.0, WavLM, HuBERT, BEATs 등

Downstream Task

- Results

• 전체적으로 AxLSTM은 각 downstream task에서 우수한 성능을 달성함

Model 성능 비교

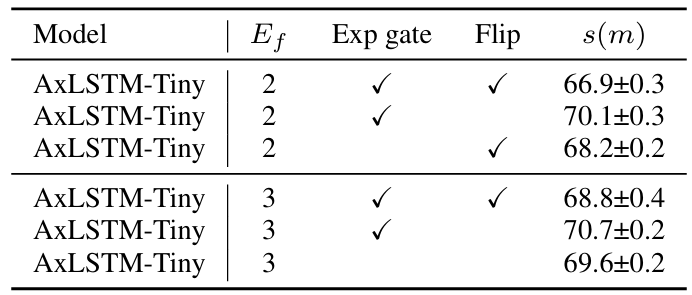
• Ablation Study
  • Expansion factor $E_{f}=3$으로 설정했을 때 최적의 성능을 달성함

Expansion Factor 별 성능

• Tiny model에서는 $(4,8)$의 patch size를 사용했을 때 뛰어난 성능을 보임

Patch Size 별 성능

• Bidirectional modeling 보다 gating mechanism이 더 효과적임

Exponential Gating과 Flipping의 효과