[Paper 리뷰] Audio Mamba: Selective State Space for Self-Supervised Audio Representations

Audio Mamba: Selective State Spaces for Self-Supervised Audio Representations

---

• 최근 selective state space model이 주목받고 있음
• Audio Mamba
  • Audio representation learning을 위해 selective state space model에 self-supervised learning을 적용 
  • Randomly masked spectrogram patch를 통해 general-purpose audio representation을 학습
• 논문 (INTERSPEECH 2024) : Paper Link

---

1. Introduction

• Transformer는 multiple domain과 data modality에 대한 representation learning을 위해 주로 사용됨
  • BUT, Transformer는 scaled dot-product attention operation으로 인해 quadratic complexity를 가짐
    - 이로 인해 large sequence에는 적용하기 어려움
  • 이러한 Transformer의 한계를 극복하기 위해 State Space Model (SSM)이 등장함
    1. 이때 SSM은 first-order differential equation set으로 govern 되는 sequence model로 볼 수 있음
       
    2. SSM은 다양한 downstream task에 적용되며 inherent resolution invariance와 뛰어난 long-range modeling capability를 보임

-> 그래서 SSM을 audio representation learning에 도입한 Audio Mamba를 제안

 

• Audio Mamba
  • SSM과 masked predictive modeling을 활용하여 self-supervised model을 구성 
  • Randomly masked spectrogram patch로부터 general-purpose audio representation을 학습

< Overall of Audio Mamba >

• SSM에 self-supervised learning을 적용한 audio representation model
• 결과적으로 downstream task에서 기존보다 우수한 성능을 달성

2. Method

- Prerequisites: State Space Models

• Structured State Space Sequence model (S4)는 linear time invariant sequence model으로써, continuous system에 기반하여 input $x(t)\in\mathbb{R}$을 latent state $h(t)\in\mathbb{R}^{N}$을 통해 $y(t)\in\mathbb{R}$로 mapping 함
  • 이때 evolution parameter $\mathbf{A}$와 projection parameter $\mathbf{B},\mathbf{C}$는:
    (Eq. 1) $h'(t)=\mathbf{A}h(t)+\mathbf{B}x(t)$
    (Eq. 2) $y(t)=\mathbf{C}h(t)$
    
  • (Eq. 1), (Eq. 2)는 additional timescale parameter $\Delta$와 함께 일반적으로 zero-order hold인 discretization rule을 통해 discretize 됨:
    (Eq. 3) $\bar{\mathbf{A}}=\exp(\Delta\mathbf{A})$
    (Eq. 4) $\bar{\mathbf{B}}=(\Delta\mathbf{A})^{-1}\left(\exp(\Delta \mathbf{A})-I\right)\cdot \Delta\mathbf{B}$
  • 그러면 S4는 (Eq. 1), (Eq. 2)의 discretized version으로 볼 수 있음:
    (Eq. 5) $h_{t}=\bar{\mathbf{A}}h_{t-1}+\bar{\mathbf{B}}x_{t}$
    (Eq. 6) $y_{t}=\mathbf{C}h_{t}$
  • 결과적으로 $\text{SSM}(\bar{\mathbf{A}},\bar{\mathbf{B}},\mathbf{C})(\cdot)$은 input sequence $\mathbf{x}$와 kernel $\bar{\mathbf{K}}\in\mathbb{R}^{M}$ 간의 global convolution으로 compute 됨:
    (Eq. 7) $\bar{\mathbf{K}}=\left(\mathbf{C}\bar{\mathbf{B}}, \mathbf{C}\overline{\mathbf{AB}}, ..., \mathbf{C}\bar{\mathbf{A}}^{M-1}\bar{\mathbf{B}}\right)$
    (Eq. 8) $\mathbf{y}=\mathbf{x}*\bar{\mathbf{K}}$
    - $M$ : input $\mathbf{x}$의 length
  • 앞선 (Eq. 5)-(Eq. 8)에서 S4 model의 parameter는 input에 condition 되지 않고 time-invariant 함
    - Mamba의 경우 parameter $\mathbf{B},\mathbf{C}\in\mathbb{R}^{B\times L\times N}$과 $\Delta \in \mathbb{R}^{B\times L\times D}$가 input $\mathbf{x}\in\mathbb{R}^{B\times L\times D}$의 function이고, context-aware 하므로 selective structured state space에 해당함 

Overview

- Self-Supervised Audio Mamba: SSAM

• Creating Patches and Random Masking
  • Input spectrogram $\mathbf{x}\in\mathbb{R}^{T\times F}$에 대해, 논문은 $t\times f$ shape의 non-overlapping patch를 compute 하여 $\mathbf{x}_{p}\in\mathbb{R}^{N\times (t\cdot f)}$ patch를 생성함
    - $N$ : patch 수
  • 이후 해당 patch를 flatten 하고 $\mathbb{R}^{N\times d_{m}}$ dimension space로 linearly project 한 다음, positional information encoding을 위한 fixed sinusoidal positional embedding을 add 함
    - 이때 sequence beginning에 representative class token을 add 함
  • 다음으로 unstructured masking strategy를 활용하여 input patch의 $50\%$를 randomly mask 하고, 해당 masked patch를 learnable mask token으로 replace 함
    
  • 결과적으로 얻어지는 encoder input은:
    (Eq. 9) $\mathbf{x}'=\left[\text{cls},\mathbf{x}_{p}^{1},\mathbf{x}_{p}^{2},...,\mathbf{x}_{p}^{N}\right]+E_{pos}$
• Encoding
  • Partially masked patch는 Mamba encoder에 전달됨
    1. Mamba block은 expansion factor $E$로 $d_{m}$ dimensional input patch를 expand 한 다음, 다시 $d_{m}$ dimension으로 project 함
    2. 기존 Mamba는 $E=2$의 expansion factor를 사용하지만, 논문에서는 $E=3$, internal dimension $d_{state}=24, d_{conv}=4$의 wider Mamba block을 사용함
       
  • 결과적으로 해당 process를 통해 encoded representation $\mathbf{z}=\text{enc}(\mathbf{x}'),\,\,\, \mathbf{z}\in\mathbb{R}^{(N+1)\times d_{m}}$을 얻음
• Reconstruction
  • Single hidden layer $\text{MLP}$는 encoded representation $\mathbf{z}$로부터 patch를 reconstruct 함:
    (Eq. 10) $ \mathbf{y}'=\text{Linear}_{(t\cdot f)}\left(\sigma\left(\text{Linear}_{d_{m}}(\mathbf{z})\right)\right)$
    - $\text{Linear}_{d}$ : dimension $d$로의 parameterized linear projection
    - $\sigma$ : GELU non-linear activation
  • 이후 $\mathbf{y}'$에서 $\text{cls}$ token을 remove 하여 reconstructed output $\mathbf{y}\in\mathbb{R}^{N\times (t\cdot f)}$를 얻음 
  • Pre-training 시 논문은 original input patch $\mathbf{x}_{p}$와 predicted reconstruction $\mathbf{y}$ 간의 Mean Squared Error를 사용함
    - Downstream evaluation 시에는 random masking, reconstruction network가 discard 되고 latent representation $\mathbf{z}$가 사용됨

3. Experiments

- Settings

• Dataset : AudioSet
• Comparisons : Wav2Vec 2.0, WavLM, HuBERT, BEATs 등

- Results

• 전체적으로 Audio Mamba가 가장 뛰어난 성능을 보임

Model 성능 비교

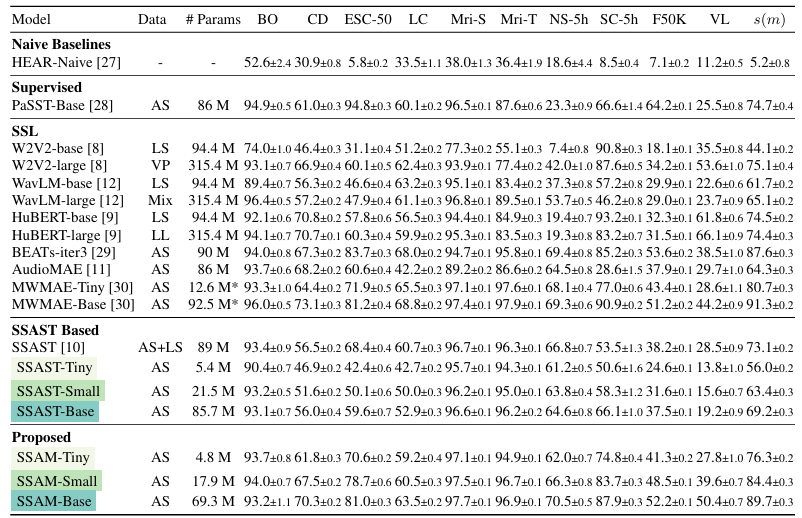
• Ablations
  • $(4,8), (4,16), (8,16)$의 patch size에 대해 SSAM이 SSAST 보다 더 나은 성능을 보임

Patch Size 별 성능

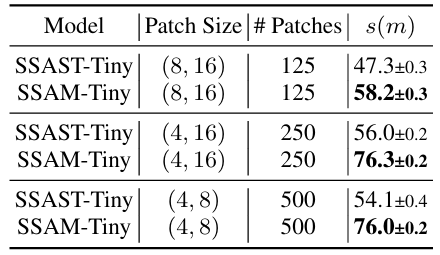
• 더 많은 pre-training data를 사용할수록 더 우수한 성능을 달성할 수 있음

Pre-training Data Size 별 성능

• 여러 SSM 중에서도 Mamba를 활용했을 때 최상의 성능을 얻을 수 있음

SSM 별 성능