[Paper 리뷰] ATP-TTS: Adaptive Thresholding Pseudo-Labeling for Low-Resource Multi-Speaker Text-to-Speech

ATP-TTS: Adaptive Thresholding Pseudo-Labeling for Low-Resource Multi-Speaker Text-to-Speech

---

• Text-to-Speech는 low-resource scenario에서는 활용하기 어려움
• ATP-TTS
  • Adaptive Thresholding을 통해 적절한 pseudo-label을 select
  • 이후 contrastive learning perturbation으로 enhance 된 Automatic Speech Recognition model을 활용하여 latent representation을 predict
• 논문 (ICASSP 2025) : Paper Link

---

1. Introduction

• Glow-TTS, VITS, NaturalSpeech와 같은 supervised Text-to-Speech (TTS) model은 human speech의 rich semantic/acoustic information을 활용하여 realistic synthetic speech를 생성함
  • BUT, 해당 방식은 paired $\langle \text{speech-text}\rangle$ label에 의존하므로 labeled data가 scarce 한 low-resource scenario에서는 활용하기 어려움
  • 이를 해결하기 위해 WavLM, HuBERT와 같은 Self-Supervised Learning (SSL) approach를 활용할 수 있음
    1. SSL pre-training을 위해서는 noise interference를 mitigate 하고 unsupervised loss의 fixed threshold에 대한 의존성을 avoid 할 수 있어야 함
    2. 특히 self-supervised dataset에서 acoustic feature의 meaningful semantic information을 extract 해야 함
       - 기존에는 curriculum pseudo-labeling strategy를 사용하거나 HierSpeech와 같이 Wav2Vec 2.0 embedding을 활용함

-> 그래서 low-resource scenario를 위한 SSL-based TTS model인 ATP-TTS를 제안

 

• ATP-TTS
  • VITS framework를 기반으로 Wav2Vec 2.0 representation을 incorporate 하여 data scarcity, target domain generalization 문제를 해결
  • Adaptive Thresholding method를 통해 pseudo-label을 생성하는 criterion을 구축하고 contrastive task를 통해 semantic, speech information을 decouple 하여 better prior condition을 획득

< Overall of ATP-TTS >

• Adaptive Thresholding, Contrastive Learning을 활용한 low-resource TTS model
• 결과적으로 기존보다 우수한 합성 성능을 달성

2. Method

- Self-Supervised Pre-Training

• Unlabled data에 대한 pre-training을 수행하기 위해 speech chain model을 통해 prior knowledge를 추출함
  • Wav2Vec 2.0의 self-supervised Automatic Speech Recognition (ASR) algorithm $f_{asr}(\cdot)$은 audio-only data를 analyze 하는 데 사용되고, dynamic thresholding, contrastive task를 통해 quasi-textual feature sequence $Z=(z_{1},...,z_{t})$를 생성함
  • 각 $z_{i}$는 latent variable로 VITS-based TTS generation function에 전달되어 spectrogram sequence $\hat{y}=g_{tts}(f_{asr}(x))$를 얻음
  • 모든 input은 pure audio에서 derive 되고 unsupervised loss는 pseudo-labeling, negative sample recognition을 통해 calculate 됨
• Pseudo Labeling
  • 먼저 speech signal에 random data augmentation을 통해 information perturbation을 적용함
    
    1. $N$을 batch size, $u_{n}$을 $n$-th unlabled speech data라고 하면, Weak augmentation $\omega(u_{n})$은 parameter equalization, formant shifting 적용을 의미함
       - Strong augmentation $\Omega(u_{n})$은 augmentation의 random combination 적용을 의미함
    2. 그러면 서로 다른 perturbation을 가지는 speech sample pair는 Wav2Vec 2.0 module에 전달되고,
    3. 15-th Transformer block output의 1024-dimensional latent variable $(r_{1},...,r_{t})$는 각 timestep $t$에서 추출되어 ASR generator에 input 됨
  • ASR generator는 batch normalization, linear fully connected layer, 3-stride를 가지는 1D convolution layer로 구성됨
    1. 이때 pre-processing을 통해 pseudo-label을 생성하는 기존 방식과 달리, dimensionality reduction을 위해 PCA 대신 time axis를 따라 batch normalization을 적용함
    2. 3-stride convolution window는 50Hz로 originally sample 된 Wav2Vec 2.0 feature $r_{i}$를 16Hz로 adjust 함
       - Maximum predicted logit이 same word category에 해당하는 consecutive output의 경우, 해당 output은 uniform distribution을 따라 timestep axis로 randomly merge 됨
  • $q_{n}=p_{m}(r_{t}|\omega(u_{n}))$을 timestep $t$에서 data $r_{t}$에 대한 predicted distribution이라고 하자
    1. $\hat{p}_{m}(\hat{r}_{t}|\omega(u_{n}))$을 softmax-normalized logit, $\lambda_{pl}$을 $\mathcal{L}_{pl}$의 scale factor라고 하면
    2. Dynamic threshold $\beta_{t}(c)$와 unsupervised pseudo-label loss는 다음과 같이 얻어짐:
       (Eq. 1) $\beta_{t}(c)=\frac{\sigma_{t}(c)}{\max\{\max_{c}\sigma_{t},N-\sum_{c}\sigma_{t}\}}$
       (Eq. 2) $\mathcal{L}_{pl}=\frac{\lambda_{pl}}{N}\sum_{n=1}^{N}\mathbb{1}[\max(q_{n})>\mathcal{T}_{\tau}(\arg\max(q_{n}))]\cdot H[\hat{q}_{n},p_{m}(r_{t}|\Omega(u_{n}))]$
       - $\sigma_{t}(c)$ : time $t$에서 phoneme class $c$를 predict 할 probability
       - $N-\sum_{c}\sigma_{t}(c)$ : unused unlabled data의 양
  • 이를 통해 training beginning에서 unused unlabled data의 quantity가 dominate 하지 않을 때까지 모든 learning estimates가 0에서부터 gradually improve 됨 
    1. 해당 warm-up process의 duration은 unlabled data quantity $N$과 learning difficulty metric $\sigma_{t}(c)$의 growth rate에 따라 달라짐
    2. 여기서 $\tau$를 pre-defined fixed threshold라고 하면, adjustable threshold는 $\mathcal{T}_{\tau}(c)=\mathcal{M}(\beta_{t}(c))\cdot \tau$와 같이 얻어짐
       - $\mathcal{M}(x)=x/(2-x)$ : 최댓값이 $1/\tau$보다 작은 monotonically increasing convex function
       - 해당 non-linear mapping은 low threshold에서 $\beta_{t}(c)$에 small growth rate를 제공하고, large $\beta_{t}(c)$의 경우 perturbation에 대한 sensitivity를 increase 함
  • 결과적으로 flexible threshold는 각 iteration을 통해 update 되고, well-learned class에 대한 threshold는 higher-quality sample을 selectively choice 할 수 있도록 raise 됨
    - 모든 class가 reliable accuracy를 달성하면 threshold는 $\tau$로 converge 함
• Contrastive Prior Encoding
  • Prior encoder는 linear layer, attention module, 1D convolution mapping layer로 구성됨
    • Attention module에서 input $k,q,v$는 convolution layer output $h$로부터 얻어짐
      - Attention head의 logit은 mapping layer에 전달되어 prior distribution을 predict 함
    • Prior encoder input은 softmax를 적용하지 않은 strong/weak augmentation의 $r_{t}^{1},r_{t}^{2}$와 concatenated ASR generator output의 concatenated pair를 사용함
      - 이를 통해 prior encoder는 ASR generator에 적용된 pseudo-label loss와 관계없이 generalized feature sequence를 receive 할 수 있음
  • 그러면 contrastive loss는:
    (Eq. 3) $\mathcal{L}_{contr}=\sum_{t=1}^{T}\frac{\exp(\text{sim}(r_{t}^{1},r_{t}^{2})/k)}{\sum_{\tau\in\{t\}\cup I_{t}}\exp(\text{sim}(r_{t}^{1},r_{\tau}^{1})/k)}+\sum_{t=1}^{T} \frac{\exp(\text{sim}(r_{t}^{2},r_{t}^{1})/k)}{\sum_{\tau\in\{t\}\cup I_{t} }\exp(\text{sim}(r_{t}^{2},r_{\tau}^{2})/k)}$
    - $r_{t}^{1},r_{t}^{2}$ : same waveform의 2개의 서로 다른 augmented perturbation에서 얻은 embedding
    - $\text{sim}(\cdot)$ : cosine similarity
    
  • 결과적으로 contrastive loss는 (Eq. 3)과 같이 $r_{t}^{1},r_{t}^{2}$에 대한 두 symmetrical term으로 구성됨
• VITS Utilization
  • Conditional VAE는 Evidence Lower BOund (ELBO)를 maximize 하여 intractable conditional marginal log-likelihood objective $\log p_{\theta}(x|c)$를 optimize 함:
    (Eq. 4) $\log p_{\theta}(x|c)\geq \mathbb{E}_{q_{\phi}(Z|X)}\log p_{\theta}(x|z)-\text{Div}\left[q_{\phi}(z|x)||p_{\theta}(z|c)\right]$
    - $p_{\theta}(x|c)$ :  condition $c$ (text, alignment)가 주어졌을 때 $x$의 distribution (waveform, spectrogram)
    - $q_{\phi}(z|x)$ : linear spectrogram $x_{lin}$을 condition으로 하는 latent variable $z$의 Gaussian distribution에 대한 posterior encoder prediction
    - $p_{\theta}(z|c)$ : condition $c$에 대한 latent variable $z$의 prior encoder conditional prior distribution
    - $\log p_{\theta}(x|z)$ : decoder의 likelihood로써 posterior distribution에서 latent variable $z$를 sampling 한 다음, spectrogram $x$를 reconstruct 함
    - $\text{Div}\left[q_{\phi}(z|x)||p_{\theta}(z|c)\right]$ : posterior, prior encoder의 KL-divergence
  • 논문에서 $\theta$로 parameterize 된 prior encoder는 condition $c_{r^{2}}$이 주어지면 latent variable $z_{c}$의 conditional prior distribution $p_{\theta}(z_{c}|c_{r^{2}})$을 predict 함
    1. 해당 predicted prior distribution은 Monotonic Alignment Search (MAS)로 전달되고,
    2. MAS는 flow module에서 전달된 predicted result $z_{q}$와 함께 Gaussian distribution $\mathcal{N}(\mu,\sigma)$에 incorporate 하여 hard alignment matrix $A$를 compute 함
       - 그러면 prior distribution prediction은 $p_{\theta}(z_{c}|c_{r^{2}},A_{pl})$이 됨
  • $q_{\phi}$로 parameterize 된 posterior encoder는 linearly pre-processed spectrum $x_{lin}$을 condition으로 하여 posterior distribution $q_{\phi}(z|x_{lin})$을 predict 함
    1. 이때 reparameterization sampling 이후 latent variable $z$의 slice $z_{slice}$가 decoder에 전달되어 spectrum을 reconstruct 함
       - 이를 통해 spectral reconstruction loss $\mathcal{L}_{recon}$을 얻을 수 있음
    2. 이후 complete latent variable $z$는 flow module을 통과하여 conditional marginal KL-divergence를 compute 하는데 필요한 $z_{q}$를 제공하고, 이때 loss function은:
       (Eq. 5) $\mathcal{L}_{kl}=\text{Div}\left[q_{\phi}(z|x_{lin})||p_{\theta}(z_{c}|c_{r^{2}},A_{pl})\right]$
  • 추가적으로 논문은 VITS의 adversarial loss $\mathcal{L}_{adv}$, feature matching loss $\mathcal{L}_{fm}$을 사용함
  • 결과적으로 얻어지는 complete pre-training loss는:
    (Eq. 6) $\mathcal{L}_{pre}=\mathcal{L}_{recon}+\mathcal{L}_{kl}+\mathcal{L}_{pl}+\mathcal{L}_{contr}+\mathcal{L}_{adv}+\mathcal{L}_{fm}$

Pre-Training Process

- Supervised Fine-Tuning

• Fine-tuning process에서 ASR feature extractor는 VITS의 text encoder로 replace 됨
  • 여기서 attention layer, 1D convolution mapping layer는 pre-training stage의 prior encoder weight를 share 함
    1. 그러면 model은 text phoneme이 condition으로 주어졌을 때 $p_{\theta}(x|c_{text})$를 estimate 함
    2. MAS module은 각 text에 해당하는 spectrogram length를 output 한 다음, input spectrogram과 함께 random duration predictor에 전달되어 $\mathcal{L}_{dur}$를 calculate 함
  • Posterior encoder, reference encoder의 parameter는 pre-training 중에 spectrogram과 speaker representation에만 condition 되므로 fine-tuning 시에는 frozen 됨
    1. 여기서 decoder는 training process에 사용되지 않고 $\mathcal{L}_{dur},\mathcal{L}_{kl}$만 사용됨
       - Duration loss $\mathcal{L}_{dur}$는 VITS를 따르고 KL divergence loss는 $\mathcal{L}_{kl}=\text{Div}\left[q_{\phi}(z|x_{lin})||p_{\theta}(z|c_{text},A_{text})\right]$
    2. 그러면 overall loss는:
       (Eq. 7) $\mathcal{L}_{tune}=\lambda_{kl}\cdot \mathcal{L}_{kl}+\mathcal{L}_{dur}$
       - $\lambda_{kl}$ : weighting factor

3. Experiments

- Settings

• Dataset : AISHELL
• Comparisons : VITS, YourTTS, Transfer-TTS

- Results

• 전체적으로 ATP-TTS의 성능이 가장 우수함

Model 성능 비교

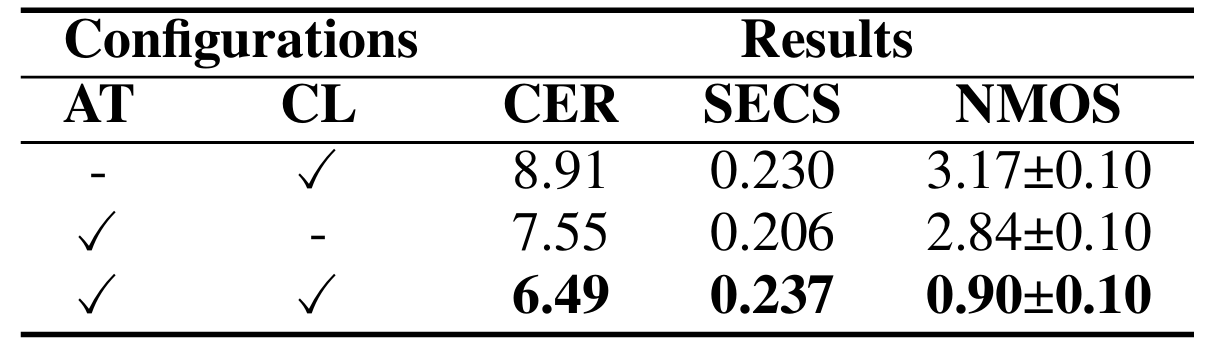
• Ablation Study
  • Adaptive Thresholding (AT), Contrastive Learning (CL)을 제거하는 경우 성능 저하가 발생함

Ablation Study