[Paper 리뷰] Flowtron: An Autoregressive Flow-based Generative Network for Text-to-Speech Synthesis

Flowtron: An Autoregressive Flow-based Generative Network for Text-to-Speech Synthesis

---

• Style transfer, speech variation을 향상하기 위해 autoregressive flow-based generative network를 활용할 수 있음
• Flowtron
  • Training data의 likelihood를 maximizing 하여 optimize 되고 simple, stable training을 지원
  • Timbre, expressivity, accent를 modulate할 수 있는 latent space에 대한 invertible mapping을 학습
• 논문 (ICLR 2021) : Paper Link

---

1. Introduction

• 최근의 Text-to-Speech (TTS)는 speech에 대한 충분한 control을 제공하지 못함
  • Context에 따라 다른 emphasis나 emotion으로 speak할 수 있지만 particular reading을 label 하는 것은 어렵기 때문
  • 특히 dataset의 unlabeled characteristic을 활용하기 위해 unsupervised learning으로 formulate할 수 있음 
    1. Latent space에 representation이 있다고 가정하여 model이 해당 representation을 학습하는 방식
    2. 이후 해당 representation을 manipulate하여 generative model output을 control 가능
  • 한편으로 최근의 expressive TTS는 text와 non-textual information의 learned latent embedding을 combine 하는 방식을 사용함 
    1. BUT, 해당 방식은 embedding dimensionality에 대한 가정을 미리 결정해야 한다는 단점이 있음 
    2. 따라서 기존의 embedding은 speech를 reconstruction하는데 필요한 모든 non-textual information을 포함하는 것이 보장되지 않음
       - Model은 dummy, uninterpretable latent dimension과 capacity 문제를 가지게 됨
    3. 추가적으로 fixed length embedding으로 인해 time에 따른 speech characteristic을 manipulate 할 수 없음
       - VAE, GAN 등은 manipulated latent embedding을 제공할 수 있지만 training이 어렵고 latent space에서 MLE를 수행하기 위해 implicit generative model이나 ELBO estimation에 의존함

-> 그래서 speech variation을 효과적으로 반영할 수 있는 autoregressive TTS model인 Flowtron을 제안

 

• Flowtron
  • Mel-spectrogram에 대한 distribution을 spherical Gaussian으로 parameterize된 latent $\mathbf{z}$-space에 mapping 하는 invertible function을 학습
    - Glow-TTS, Flow-TTS와 달리 autoregressive architecture를 기반으로 함
  • Flowtron의 formulation을 통해 $\mathbf{z}$-space에 structure를 impose 하고 Gaussian mixture로 parameterize 가능
    - Zero-mean spherical Gaussian prior를 가지는 sample을 생성하고 variance을 adjust 하여 variation을 control 함
  • Tacotron에서 사용된 additional Prenet, Postnet layer를 제거하고 compound loss function에 대한 의존성 없이 data의 likelihood를 maximize 하여 높은 $\sigma^{2}$ value에서도 sharp mel-spectrogram을 생성 가능

< Overall of Flowtron >

• Mel-spectrogram 합성을 위한 autoregressive flow-based generative network
• 결과적으로 기존보다 뛰어난 합성 품질을 달성

2. Method

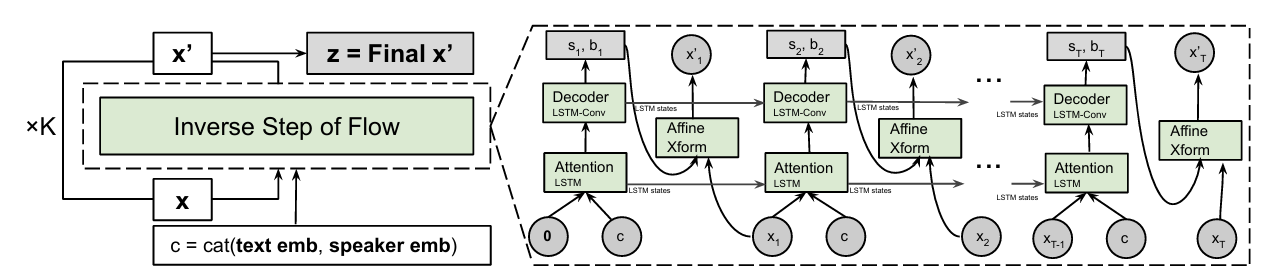
• Flowtron은 mel-spectrogram frame sequence를 생성하는 autoregressive flow와 같음
  • Normalizing flow는 known distribution $p(\mathbf{z})$에서 latent variable을 sampling 하고 invertible transfromation series를 적용하여 target distribution $p(\mathbf{x})$로부터 sample을 생성함
  • 여기서 invertible transformation $\mathbf{f}$를 flow step이라고 함:
    (Eq. 1) $\mathbf{x}=\mathbf{f}_{1}\circ\mathbf{f}_{2}\circ ...\mathbf{f}_{k}(\mathbf{z})$
  • 각 transformation은 invertible 하므로 variable change를 사용하여 target distribution $p(\mathbf{x})$의 exact log-likelihood를 directly evaluate 할 수 있음:
    (Eq. 2) $\log p_{\theta}(\mathbf{x})=\log p_{\theta}(\mathbf{z})+\sum_{i=1}^{k}\log |\det (\mathbf{J}(\mathbf{f}_{i}^{-1}(\mathbf{x})))|$
    (Eq. 3) $\mathbf{z}=\mathbf{f}_{k}^{-1}\circ\mathbf{f}_{k-1}^{-1}\circ ... \mathbf{f}_{1}^{-1}(\mathbf{x})$
    - $\mathbf{J}$ : inverse transform $\mathbf{f}_{i}^{-1}(\mathbf{x})$의 Jacobian
  • 여기서 latent distribution $p(\mathbf{z})$를 cleverly choosing 하는 경우 exact log-likelihood는 simple하고 tractable 해짐

Overall of Flowtron

- Latent Distributions

• Latent distribution $\mathbf{z}$에 대해 2가지 simple distribution을 고려할 수 있음
  • Zero-mean spherical Gaussian, fixed/learnable parameter를 가지는 spherical Gaussian mixture:
    (Eq. 4) $\mathbf{z}\sim\mathcal{N}(\mathbf{z};0,I)\,\,\, \text{or}\,\,\, \mathbf{z}\sim\sum_{k}\hat{\phi}_{k}\mathcal{N}(\mathbf{z};\hat{\mu}_{k},\hat{\Sigma}_{k})$
  • Zero-mean spherical Gaussian은 simple log-likelihood를 가지고 spherical Gaussian mixture는 inherent cluster를 가짐

- Invertible Transformations

• Normalizing flow는 coupling layer를 활용하여 구성되고, Flowtron은 autoregressive affine coupling layer를 채택함
  • Latent variable $\mathbf{z}$는 resulting mel-spectrogram sample과 동일한 dimension, frame을 가짐
  • Previous frame $\mathbf{z}_{1:t-1}$은 scale, bias term $\mathbf{s}_{t}, \mathbf{b}_{t}$를 생성하여 succeeding time step $\mathbf{z}_{t}$를 affine transform 함:
    (Eq. 5) $(\log \mathbf{s}_{t},\mathbf{b}_{t})=\text{NN}(\mathbf{z}_{1:t-1},\text{text},\text{speaker})$
    (Eq. 6) $\mathbf{f}(\mathbf{z}_{t})=(\mathbf{z}_{t}-\mathbf{b}_{t})\div \mathbf{s}_{t}$
    (Eq. 7) $\mathbf{f}^{-1}(\mathbf{z}_{t})=\mathbf{s}_{t}\odot \mathbf{z}_{t}+\mathbf{b}_{t}$
    - $\text{NN}()$ : autoregressive causal transformation으로써 affine coupling layer는 reversible transformation이지만 $\text{NN}()$은 invertible 할 필요가 없음
  • 논문은 scaling, bias term을 얻기 위해 $0$-vector를 사용하고, 이는 affine transform $\mathbf{z}_{1}$를 의미
    - 해당 $0$-vector constant는 first $\mathbf{z}$가 always known임을 보장함
  • Affine coupling layer를 사용하면 $\mathbf{s}_{t}$ term만이 mapping volume을 변경하고 loss에 variable change를 add 할 수 있음
    1. 해당 term은 non-invertible affine mapping에 대해서도 penalize 할 수 있음:
       (Eq. 8) $\log | \det (\mathbf{J}(\mathbf{f}_{coupling}^{-1}(\mathbf{x})))|=\log |\mathbf{s}|$
    2. Likelihood를 evaluate 하기 위해서는 mel-spectrogram을 text, optional speaker ID에 따라 condition 된 flow의 inverse step에 전달하고, log penalty를 adding 한 다음, Gaussian likelihood에 따라 evaluate 함
  • 해당 setup을 기반으로 mel-spectrogram frame의 ordering을 reversing 할 수 있음
    1. 따라서 논문은 flow의 even step에서 frame order를 reverse 하여 flow step을 input sequence에 대한 full pass로 정의함
    2. 이를 통해 Flowtron은 causal, invertiblity를 유지하면서 time에 따라 forward/backward로 depdendency를 학습할 수 있음

- Model Architecture

• Flowtron은 Tacotron의 Prenet, Postnet layer를 제거하여 구성됨
  • 먼저 text encoder는 Tacotron2의 text encoder에서 batch-norm을 instance-norm으로 대체하여 사용함
    1. Content-based tanh attention을 도입하여 model을 location sensitive 하게 만듦 
    2. Mel encoder는 Gaussian mixture의 parameter를 예측하는 역할을 수행하고 모든 token에 대해 encoder output과 channel-wise concatentate 된 speaker embedding을 사용함
    3. 추가적으로 speaker ID로 condition 되지 않은 model에 대해 single shared embedding을 사용함
  • Latent variable $\mathbf{z}$에 대해 closest flow step은 추론 시 model에서 제공된 $\mathbf{z}$-value에서 extra frame을 prune하는 gating mechanism을 가지고 있음
    - $\mathbf{z}$-value length는 flow의 next step에서는 fix 됨

Decoder

- Inference

• 추론은 trained model이 주어졌을 때 spherical Gaussian이나 Gaussian mixture에서 $\mathbf{z}$를 sampling 하고 (Eq. 1)과 같은 forward direction $\mathbf{f}$를 통과시키는 과정
  • 여기서 Gaussian mixture의 parameter는 fix 되거나 Flowtron을 통해 predict 됨
    
  • Training 중에 낮은 standard deviation에서 $\mathbf {z}$를 sampling 하면 더 나은 mel-spectrogram을 생성할 수 있음
    - 결과적으로 논문은 $\sigma^{2}=1$로 training 하고 inference result는 $\sigma^{2}=0.5$를 사용함

- Posterior Inference

• 아래 그림과 같이 mel-spectrogram에 존재하는 speech characteristic은 $\mathbf{z}$-space region으로 cluster 되어 있음
  • 따라서 latent distribution을 prior $q(\mathbf{z})=\mathbf{N}(0,I)$로 취급하고 evidence $\zeta_{1:m}$에 따라 condition 된 flow model $q(\mathbf{z}| \zeta_{1:m})$의 latent space에 대한 posterior를 얻을 수 있음
    - 이는 $\zeta_{i}=\mathbf{f}^{-1}(\mathbf{x}_{i})$를 사용하여 latent space에 mapping 된 $m$개의 data observation $\mathbf{x}_{i}$에 해당
  • Covariance matrix $\Sigma$가 있는 경우 Gaussian likelihood function을 사용하여 posterior를 $q(\mathbf{z}|\zeta_{1:m})=\mathcal{N}(\mu_{p},\Sigma_{p})$와 같이 analytically compute 할 수 있음
  • 이때 $\bar{\zeta}$를 $\zeta_{i}$의 mean이라 하고, $\lambda$를 hyperparameter로 사용하여 posterior의 parameter를 다음과 같이 정의할 수 있음:
    (Eq. 9) $\mu_{p}=\frac{\frac{m}{\lambda}\bar{\zeta}}{\frac{m}{\lambda}+1},\,\,\, \Sigma_{p}=\frac{1}{\frac{m}{\lambda}+1}I$

$t$-SNE 결과

3. Experiments

- Settings

• Dataset : LJSpeech, LibriTTS
• Comparisons : Tacotron2

- Results

• Flowtron은 Tacotron2보다 높은 MOS를 달성함

MOS 비교

• Speech Variation
  • Flowtron은 prior distribution $\mathbf{z}\sim\mathcal{N}(0,\sigma^{2})$에서 sampling을 수행하고 $\sigma^{2}$를 adjust 하여 variation을 adjust 할 수 있음
  • $\sigma^{2}=0$은 variation을 completely remove 하고 model bias에 기반한 output을 생성함
    - $\sigma^{2}$이 커지는 경우 speech variation이 증가함
  • $\sigma^{2}\in\{0.0,0.5,1.0\}$에 대한 spectrogram을 비교해 보면, Flowtron은 $\sigma^{2}$이 증가되었음에도 high quality speech를 생성할 수 있음
    - 특히 sharp harmonics와 well-resolved formant를 생성함

$\sigma^{2}$에 따른 Mel-Spectrogram 비교

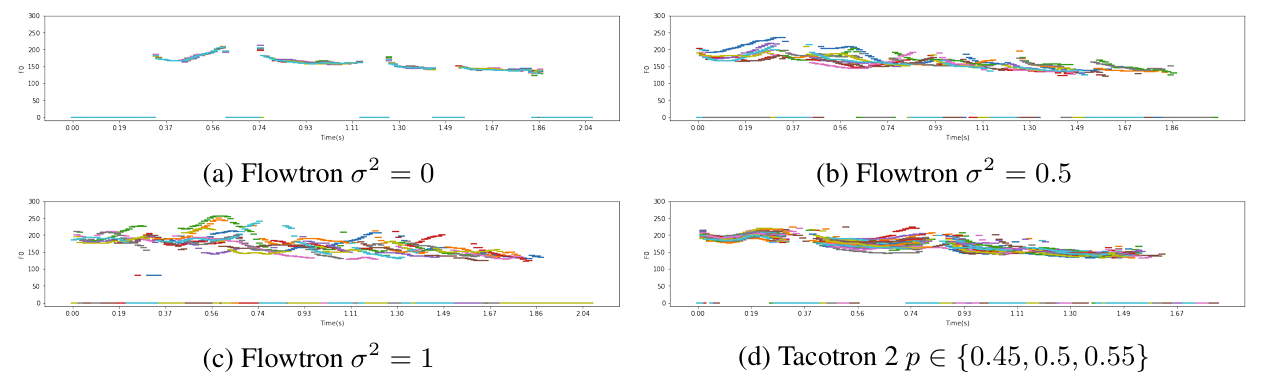
• $F_{0}$ contour 측면에서도 Flowtron은 $\sigma^{2}=0$일 때 variation이 나타나지 않지만 $\sigma^{2}$가 증가할수록 $F_{0}$ variation이 나타남
  - Prenet probability $p$ 역시 variation에 크게 영향을 미치지 않음

$F_{0}$ Contour

• Sampling the Posterior (Style Transfer)
  • Seen speaker 측면에서 Flowtron은 posterior에서 sampling 하거나 posterior/Gaussian prior를 interpolate 함으로써 monotonic speaker를 expressive 하게 합성할 수 있음
  • Unseen speaker 측면에서도 Flowtron은 surprised style을 효과적으로 반영할 수 있음

Style Transfer

• Interpolation Between Styles
  • (Eq. 9)의 parameter를 adjust 하여 baseline style (prior)와 target style (posterior)를 interpolate 하고 이를 통해 speaking style을 control 할 수 있음
  • 결과적으로 $\lambda\in\{0.1, 0.666, 1.0, 2.0\}$으로 합성된 결과를 비교해 보면, $\lambda$가 감소할수록 spectral profile은 baseline style (prior)에서 target style (posterior)로 이동함

Spectral Profile

• Visualizing Assignments
  • 각 utterance를 highest posterior probability $\arg \max_{k} p(\hat{\phi}_{k} |\mathbf{x})$를 가지는 component에 assign 하고, mel encoder를 통해 time에 따른 component assignment probability를 얻을 수 있음
  • 결과적으로 Flowtron의 각 component에 있는 information은 gender dependent 하게 나타남

Assignmment Visualization

• Translating Dimensions
  • Flowtron에 offset을 adding 하여 single mixture component의 dimension을 translating 할 수 있음
  • 결과적으로 pitch height에 대한 dimension을 변환하여 얻어진 sample은 기존과 동일한 duration을 가지지만 다른 pitch contour를 나타냄
  • 마찬가지로 word length에 대한 dimension을 변경하는 경우 pitch는 modulate 되지 않고 duation만 변화함

Dimension Translation